Das elektrische Potential
Lernziele: Das elektrische Potential
Die Studierenden können
- Verschiebearbeit von Ladungen im elektrischen Feld berechnen
- Äquipotentialflächen bestimmen und einzeichnen
- elektrische Spannungen aus gegebenen Feldgrößen bestimmen
1 Arbeit im elektrischen Feld
Befindet sich eine Ladung innerhalb eines elektrischen Feldes, so wird eine Kraft auf sie ausgeübt. Wird die Ladung nun innerhalb des Feldes bewegt, muss eine Arbeit verrichtet werden. Analog ist hier das Gravitationsfeld zu sehen, bei dem eine Arbeit verrichtet werden muss, wenn eine Masse angehoben wird, also die potentielle Energie des Objektes erhöht wird. Dieser Abschnitt ist als kurzer Vorgriff auf Modul 2 Energie und Leistung zu sehen, in welchem die elektrische Arbeit genau definiert wird.
Das Vorzeichen einer verrichteten Arbeit ist abhängig davon, ob die Arbeit auf das betrachtete System (hier: Potentielle Energie der Probeladung \(Q\) im elektrischen Feld \(\vec {E}\)) oder auf den Erzeuger dieser Arbei bezogen wird. In diesem Skript wird sich auf den Erzeuger bezogen. Muss dieser eine Arbeit verrichten, um die potentielle Energie des Systems zu erhöhen, ist die verrichtete Arbeit als negativ anzusehen. Wird eine Arbeit vom System freigesetzt, sprich die potentielle Energie der Prodeladung sinkt, ist die Arbeit positiv.
Physikalisch gesehen ist die Arbeit das Produkt aus der Kraft, die benötigt wird, um die Ladung zu bewegen, multipliziert mit der zurückgelegten Wegstrecke. Mit der Erkenntnis aus Kapitel 4.1, dass die elektrische Feldstärke der Quotient aus der Kraft auf eine Ladung pro Ladung ist (siehe Gleichung ??), lässt sich die zum Bewegen der Ladung benötigte Arbeit ermitteln.
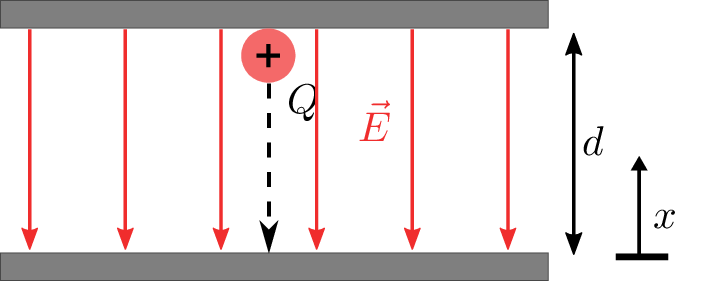
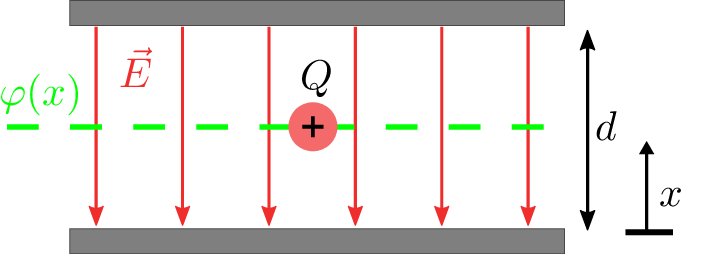
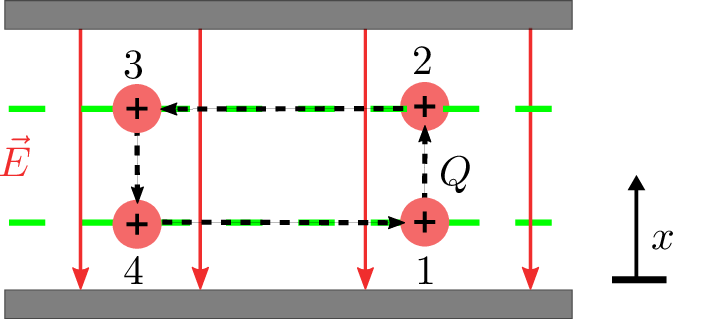
Nachfolgend soll berechnet werden, welche Arbeit \(W\) bei der positiven Probeladung \(Q\) aus Abbildung 1 freigesetzt wird, wenn sie sich entlang der Feldlinien in Richtung der negativ geladenen Leiterplatte bewegt.
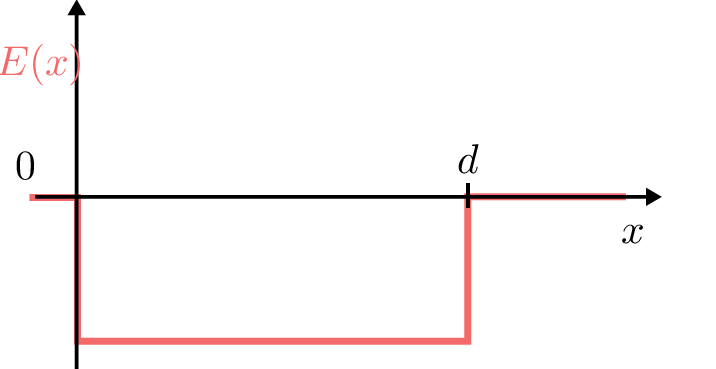
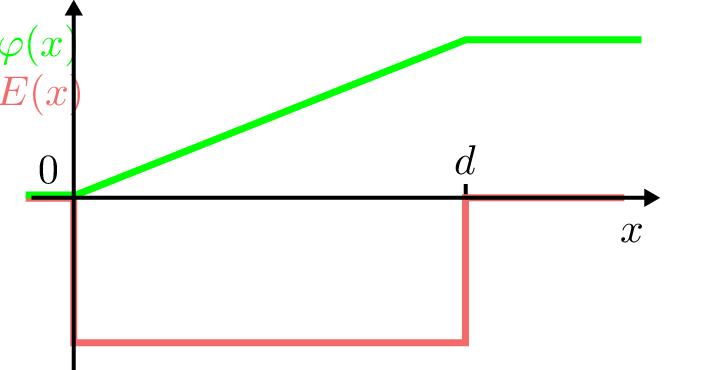
Die Verlauf der elektrischen Feldstärke sowie Richtung von \(\vec {E}\) gegenüber dem Weg \(x\) lässt sich wie in Abbildung 2 gezeigt darstellen.
\begin {equation*} W = \int _{d}^{0} \vec {F} \, d \vec {x} \end {equation*}
Da die Richtung des elektrischen Feldes \(\vec {E}\) der Raumrichtung \(x\) entgegengesetzt ist, führt ein Eliminieren der Vektorpfeile zu einem negativen Vorzeichen vor dem Integral. Durch Einsetzen der Kraft \(F\) in Gleichung ?? ergibt sich:
\begin {equation*} W = - Q \int _{d}^{0} E \cdot \mathrm {d}x \end {equation*}
Lösen des Integrals und Einsetzen der Integrationsgrenzen ergibt:
\begin {equation*} W = -Q \cdot E \, [x]_d^0 = -Q \cdot E (0-d) \end {equation*}
\begin {equation*} W = Q \cdot E \cdot d \end {equation*}
Die Differenz der zu- oder abgeführten Arbeit einer Ladung im elektrischen Feld beträgt also:
\begin {equation} \Delta W = Q \cdot E \cdot \Delta x \end {equation}
Beispiel 1
Für die in Abbildung 1 dargestellte Probeladung soll erreichnet werden, wie viel Energie auf
ihrem Weg vom Startpunkt zur negativen Platte freigesetzt wird.
Die Probeladung betrage \(Q= 1 \mu \mathrm {C}\), der Abstand zur Platte betrage 0,1 m und das elektrische Feld sei \(E= 200\) V/m.
Die Arbeit \(W\) berechnet sich dann zu
\begin {equation*} W= Q \cdot E \cdot d = 1 \cdot 10^{-6} \mathrm {C} \cdot 200 \mathrm {V/m} \cdot 0,1 \mathrm {m} = 2 \cdot 10^{-5} \mathrm {J} \end {equation*}
Analog zu einem Objekt im Gravitationsfeld führt das elektrische Feld einer Ladung Energie zu. Dadurch wird diese beschleunigt, und die potentielle Energie wird in kinetische Energie umgewandelt.
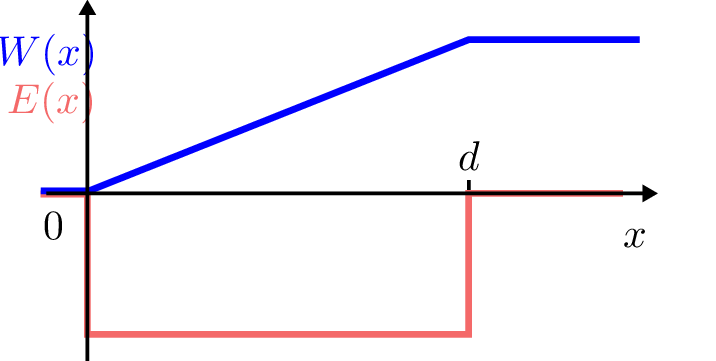
Es ist unmittelbar einsichtig, dass der Betrag der im elektrischen Feld gespeicherten und nutzbaren potentiellen Energie der Probeladung \(Q\) vom Ort \(x\) der Probeladung linear abhängig ist (siehe Abbildung 3). Verfügt die Probeladung bereits im Vorfeld über eine kinetische Energie, oder geht das elektrische Feld über den betrachteten Abschnitt hinaus, lässt sich die Gleichung um den zusätzlichen Term \(W_0\) erweitern:
\begin {equation} W(x) = Q \cdot E \cdot x + W_0 \end {equation}
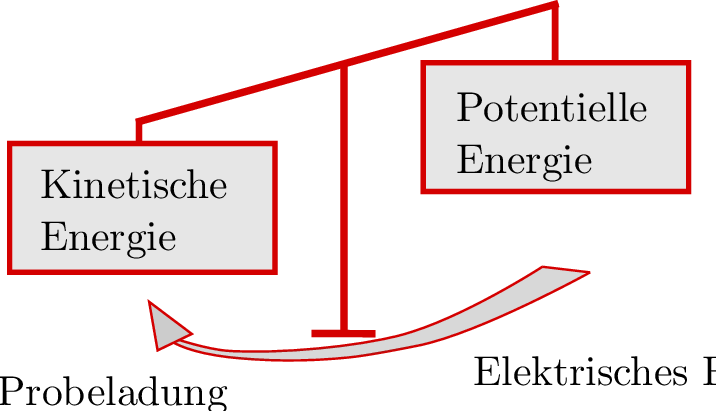
Der Übergang zwischen der im elektrischen Feld gespeicherten potentiellen Energie in die kinetische Energie der Probeladung kann über das Schaubild in Abbildung 4 dargestellt werden.
Zur allgemeinen Beschreibung muss die technisch nutzbare Feldenergie unabhängig von der Probeladung \(Q\) sein. Dazu wird die potentielle Energie auf ein Arbeitspotential normiert.
\begin {equation*} \frac {W(x)}{Q} = E \cdot x + \frac {W_0}{Q} \end {equation*}
2 Definition des elektrischen Potentials
Die potentielle Energie normiert auf die betrachtete Ladung Q ist das elektrische Potential \(\varphi \) des elektrischen Feldes. Dieses ist für jeden Punkt im Raum unabhängig von weiteren Einflussfaktoren direkt bestimmbar. Das Potentialfeld ist im Gegensatz zum elektrischen Feld ein Skalarfeld. Das bedeutet, dass jedem Punkt im Raum unabhängig von weiteren Einflussfaktoren ein eindeutiges elektrisches Potential zugeordnet werden kann, jedoch keine Richtung dieser Größe im Raum vorliegt.
\begin {equation} \varphi = \frac {W}{Q} \end {equation} \begin {equation*} [\varphi ] = \text {V} \ (\text {Volt}) \end {equation*}
Abbildung 5 zeigt ein elektrisches Homogenfeld, in welches die Potentiallinie eingezeichnet ist, auf welcher sich die Ladung \(Q\) gerade befindet. Mit zunehmender Entfernung von der positiven Platte in \(x\)-Richtung steigt das Potential an, und kann wie folgt berechnet werden:
\begin {equation} \varphi (x) = E \cdot x + \varphi _0 \label {eq:potential} \end {equation}
Die Steigung des Potentials ist durch die elektrische Feldstärke \(\vec {E}\) bestimmt. Das elektrische Potential \(\varphi \) und die elektrische Feldstärke hängen durch den negativen Gradienten des Potentials zusammen. Dieser Zusammenhang wird in Abbildung 6 verdeutlicht.
Die Beziehung kann im Homogenfeld durch die folgende Gleichung ausgedrückt werden:
\begin {equation} E = - \frac {\Delta \varphi }{\Delta x} \end {equation}
In inhomogenen, dreidimensionalen Feldern gilt die allgemeine Gleichung, bei der der Gradient von \(\varphi \) in jede Raumrichtung errechnet wird:
\begin {equation} E = - \mathrm {grad} \,\varphi (x,y,z) = \left ( \frac {\partial \varphi }{\partial x}, \frac {\partial \varphi }{\partial y}, \frac {\partial \varphi }{\partial z} \right ) \end {equation}
Um das elektrische Potential an einem Punkt vollständig zu beschreiben, muss wie in Gleichung 4 aufgeführt als notwendige Randbedingung ein Bezugspotential \(\varphi _0\) gewählt werden, welches eindeutig definiert ist. Prinzipiell ist dieses Potential beliebig wählbar, in der Regel wird jedoch eine Bezugselektrode gewählt, für die das Potential gleich null gesetzt wird. Im Fall des in Abbildung 5 gezeigten Aufbaus wäre dies:
\begin {equation*} \varphi _0 = \varphi (x=0) = 0 \end {equation*}
3 Zusammenhang zwischen Arbeit und Potential
Im homogenen elektrischen Feld ist das Potential \(\varphi \) wie Formel 4 zeigt ausschließlich von der Entfernung \(x\) zur Bezugselektrode abhängig. Dies bedeutet, dass alle Flächen, die senkrecht zum Feld stehen, ein konstantes Potential haben. Solche Flächen werden als Äquipotentialflächen bezeichnet, wie sie in Abbildung 7 mit Hilfe der grünen Linien dargestellt sind. Es muss keine Arbeit verrichtet werden, um eine Ladung entlang einer solchen Fläche zu bewegen.
Die potentielle Energie \(W_{12}\) einer Probeladung \(Q\), die durch das elektrische Feld von einem Punkt \(x_1\) nach \(x_2\) bewegt wird, kann durch die Potentialdifferenz zwischen diesen Punkten beschrieben werden. Die Reihenfolge der Indizes der Arbeit \(W_{12}\) beschreibt dabei die Bewegungsrichtung.
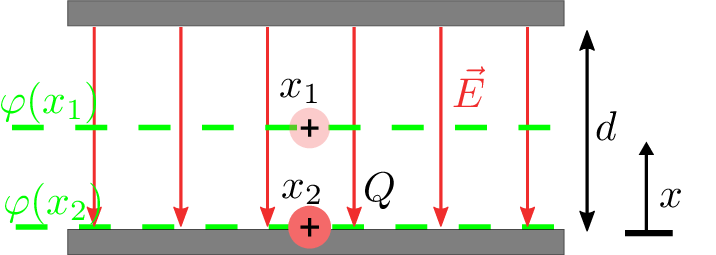
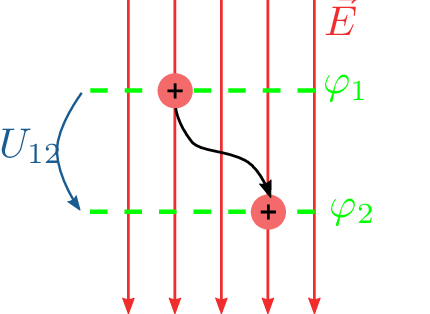
Wird eine Probeladung wie in Abbildung 7 gezeigt von der Äquipotentialfläche \(\varphi (x_1)\) nach \(\varphi (x_2)\) bewegt, nimmt sie dabei die folgende Energie auf:
\begin {equation*} W_{12} = Q \cdot (\varphi _1 - \varphi _2) \end {equation*}
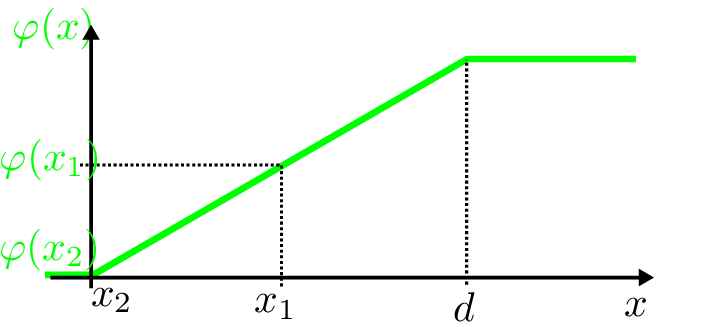
Bei der in Abbildung 8 getroffenen Wahl der Bezugsfläche von \(\varphi _2 = 0\) ergibt sich für die zugeführte Arbeit das Ergebnis:
\begin {equation*} W_{12} = Q \cdot (\varphi _1 - 0) = Q \cdot \varphi _1 \end {equation*}
Mit Hilfe des nachfolgenden Gedankenexperimentes lässt sich eine weitere zentrale Eigenschaft des elektrischen Feldes aufzeigen.
Wie in Abbildung 9 gezeigt wird eine Probeladung \(Q\) in einem Homogenfeld zwischen den Punkten 1-4 in einem geschlossenem Umlauf bewegt. Die bei diesem Vorgang zu verrichtenden Teilenergien werden betrachtet. So wird bei einer Bewegung vom Punkt 1 zu Punkt 2 eine Arbeit von \(W_{12} = Q \cdot (\varphi _1 - \varphi _2)\) verrichtet, und von Punkt 4 zu Punkt 1 die Energie \(W_{41} = Q \cdot (\varphi _4 - \varphi _1)\).
Die für einen gesamten Umlauf benötigte Energie ergibt sich durch die Aufsummierung der vier Teilenergien:
\begin {equation*} \begin {split} W_\mathrm {ges} = Q \cdot (\varphi _1 - \varphi _2) + Q \cdot (\varphi _2 - \varphi _3) + Q \cdot (\varphi _3 - \varphi _4) + Q \cdot (\varphi _4 - \varphi _1) \end {split} \end {equation*}
Da die Ladung \(Q\) in allen Termen identisch ist, ergibt sich durch das Ausklammern von \(Q\):
\begin {equation*} W_\mathrm {ges} = Q \cdot (\varphi _1 - \varphi _2 + \varphi _2 - \varphi _3 + \varphi _3 - \varphi _4 + \varphi _4 - \varphi _1) \end {equation*}
\begin {equation*} \rightarrow W_\mathrm {ges} = Q \cdot 0 = 0 \end {equation*}
Für einen geschlossenen Umlauf einer Probeladung im Homogenfeld ist also keine Energie erforderlich, da sie ausschließlich vom Anfangs- und Endpunkt der Bewegung, nicht jedoch vom gewählten Weg abhängig ist.
Folglich wird beim elektrischen Feld auch von einem wirbelfreien Quellenfeld gesprochen. Dies bedeutet, dass die Feldlinien keine geschlossenen Linien bilden, sondern jeweils einen Anfang (auf positiven Ladungen) und einen Endpunkt (auf negativen Ladungen) haben.
Diese Betrachtung gilt nicht nur für das Homogenfeld, sondern trifft auf jedes elektrostatische Feld zu.
Beispiel 2: Arbeit im Radialfeld
In folgendem Beispiel soll die Probeladung \(Q_1\) vom Abstand \(r_1\) auf den Abstand \(r_2\) an die Feste Ladung Q herangeführt werden.
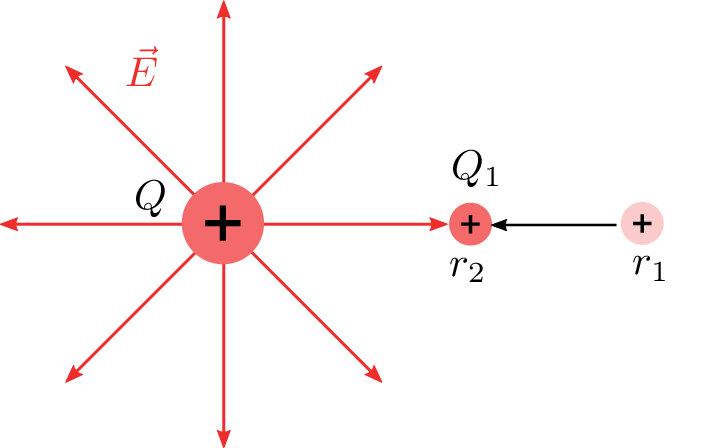
\(Q\) betrage 1 C, \(Q_1\) 1 mC. Welche Arbeit ist erforderlich, wenn \(r_1 = 1\) m und \(r_2 = 50\) cm seien?
\[ W_{12} = Q_1 \int _{r_1}^{r_2} \vec {E} \cdot d\vec {r} \] \[ W_{12} = Q_1 \int _{r_1}^{r_2} \left ( \frac {Q}{4 \pi \varepsilon _0 r^2} \right ) dr \] \[ W_{12} = Q_1 \cdot \frac {Q}{4 \pi \varepsilon _0} \int _{r_1}^{r_2} \frac {1}{r^2} dr \] Die Stammfunktion von \(\frac {1}{r^2}\) beträgt \(-\frac {1}{r}\). \[ W_{12} = Q_1 \cdot \frac {Q}{4 \pi \varepsilon _0} \left ( -\frac {1}{r} \bigg |_{r_1}^{r_2} \right ) = Q_1 \cdot \frac {Q}{4 \pi \varepsilon _0} \left ( -\frac {1}{r_2} + \frac {1}{r_1} \right ) \] wobei \(\frac {Q}{4 \pi \varepsilon _0} \frac {1}{r}\) dem Potential \(\varphi (r)\) entspricht.
\[ W_{12} = Q_1 \cdot (\varphi (r_1) - \varphi (r_2)) \]
Einsetzen der gegebenen Werte: \[ W_{12} = (1 \cdot 10^{-3} \, \text {C}) \cdot \frac {1 \, \text {C}}{4 \pi \varepsilon _0} \left ( \frac {1}{1 \, \text {m}} - \frac {1}{0{,}5 \, \text {m}} \right ) \] \[ W_{12} = -8,98755 \times 10^{6} \, \text {J} \] Folglich müssen etwa 8,99 Megajoule aufgewendet werden, um die Ladung \(Q_1\) zu verschieben.
4 Definition der elektrischen Spannung
Die aus dem elektrischen Feld für einen technischen Prozess nutzbare Energie ist durch die Potentialdifferenz zwischen Anfangs- und Endpunkt des Weges gegeben. Durch ihre fundamentale Bedeutung in der Elektrotechnik wird sie mit einem Namen und Formelbuchstaben bedacht, und wird als elektrische Spannung \(U\) bezeichnet:
\begin {equation} U_{12} = \varphi _1 - \varphi _2 \label {eq:spannung} \end {equation}
\begin {equation*} [U] = \text {V} \ (\text {Volt}) \end {equation*}
Durch die Reihenfolge der Indizes wird - analog zur Potentialdifferenz - die Zählrichtung des Spannungspfeiles angegeben. In Abbildung 10 beschreibt die Spannung \(U_{12}\) also die Potentialdifferenz zwischen den Potientialen \(\varphi _1\) und \(\varphi _2\). Durch die Eigenschaften der Äquipotentialflächen ist es hierbei vollkommen unerheblich, von welchem Punkt von \(\varphi _1\) gestartet wird und welcher Punkt auf \(\varphi _2\) das Ziel darstellt. Auch der Pfad, welcher zwischen den Punkten gewählt wird, ist für die Spannung zwischen den Punkten unerheblich.
Der Zusammenhang zwischen der elektrischen Feldstärke und dem Potential ist bereits aus Gleichung 4 bekannt und wird (bei einem Bezugspotential von \(\varphi _0 = 0)\) mit \(\varphi (x) = E \cdot x\) angegeben.
Eingesetzt in die Definition der Spannung (Gleichung 7) ergibt sich:
\begin {equation*} U = \varphi (x= d) - \varphi (x= 0) = E \cdot d - E \cdot 0 \end {equation*}
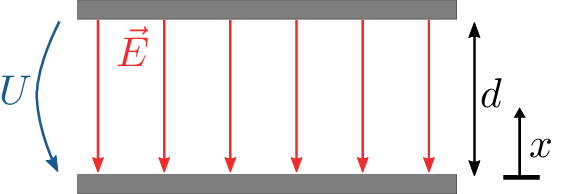
Die elektrische Spannung \(U\) kann in einem wie in Abbildung 11 dargestellten Homogenfeld wie folgt berechnet werden, sofern die Wegstrecke \(d\) parallel zu den Feldlinien liegt:
\begin {equation} U = E \cdot d \end {equation}
Alternativ kann aus einer gegebenen Spannung \(U\) bei bekannter Wegstrecke \(d\) auch die elektrische Feldstärke berechnet werden:
\begin {equation} E = \frac {U}{d} \end {equation}
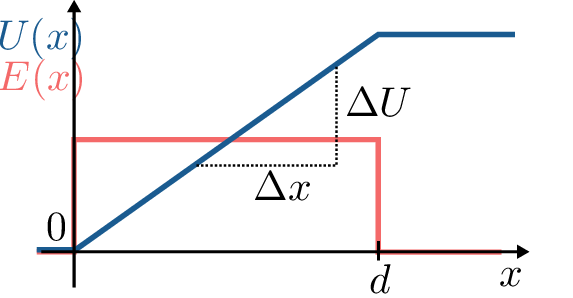
In Abbildung 12 lässt sich erkennen, dass die Spannung nichts anderes als die über die Wegstrecke \(d\) aufintegrierte Feldstärke \(E\) ist.
Während dieses Integral im Homogenfeld durch eine Multiplikation von elektrischem Feld \(E\) und Wegstrecke \(d\) ermittelt werden kann, ist dies bei inhomogenen Feldern nur durch das Lösen des Integrals möglich:
\begin {equation} U_{12} =\int _{1}^{2} \vec {E} \cdot d \vec {s} \end {equation}
Zu beachten ist hierbei, dass es sich bei dem Produkt \(\vec {E} \cdot \mathrm {d} \vec {s}\) um Vektoren handelt. Zeigen sie in die gleiche Richtung, dürfen die Vektorpfeile eliminiert werden, andernfalls muss das Skalarprodukt verwendet werden:
\begin {equation*} \vec {E} \cdot \, \mathrm {d} \vec {s} = E \cdot \mathrm {d} s \cdot \mathrm {cos} (\alpha ) \end {equation*}