GET it digital

1 Einschaltverhalten eines RC-Übertragungsgliedes

Gegeben ist das rechts dargestellte Übertragungsglied (Zweitor). Untersucht wird das Einschwingverhalten der Spannung $u_2$ am Ausgang bei Anschließen einer idealen Gleichspannungsquelle $U_q$.

Die Schaltung ist vor dem Schaltzeitpunkt $t=0$ im stationären Zustand mit $u_2(t<0) = 0$.

Stellen Sie die DGL für $u_C$ für $t \geq 0$ auf.
Bestimmen Sie die Funktion $u_C(t)$ für $t \geq 0$ inklusive aller Konstanten.
Bestimmen Sie die Funktion $u_2$ für $t \geq 0$ aus der Lösung b) für $u_C(t)$. Vereinfachen Sie soweit wie möglich.

Skizzieren Sie qualitativ die Zeitverläufe der Spannungen $u_2$, $u_{R_2}$ und $u_C$ vom stationären Zustand für $t<0$ bis die dargestellten Größen eingeschwungen sind ($t=5\tau $). Kennzeichnen Sie Zeitkonstanten, Anfangs- und Endwerte der Verläufe.

DGL für $u_C(t \geq 0)$: \begin {align*} R_1 \cdot i + R_2 \cdot i + u_C &= U_q \\ \underbrace {(R_1 + R_2) \cdot C}_{\ =\tau } \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C + u_C &= U_q \end {align*}
Zeitverlauf $u_C$ für $t\geq 0$: \begin {align*} u_{C,\mathrm {f}}=u_{C,\mathrm {h}} &= K \cdot e^{-\frac {t}{\tau }} &&\text {mit } \tau = (R_1 + R_2) \cdot C \\ u_{C,\mathrm {e}}=u_{C,\mathrm {p}} &= U_q \\ u_C = u_{C,\mathrm {f}} + u_{C,\mathrm {e}} &= K \cdot \mathrm {e}^{-\frac {t}{\tau }} + U_q \\ u_C(0) &= K \cdot \cancel {e^{0}} + U_q \overset {!}{=} 0 &&\Longrightarrow K = - U_q \\ u_C(t) &= \left (1 - \mathrm {e}^{-\frac {t}{\tau }}\right ) \cdot U_q \end {align*}
Spannung $u_2(t)$ aus $u_C(t)$ für $t \geq 0$: \begin {align*} u_2 &= i \cdot R_2 + u_C \\ &= C \cdot R_2 \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C + u_C \\ &= C \cdot R_2 \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, \left (1 - \mathrm {e}^{-\frac {t}{\tau }}\right ) \cdot U_q + \left (1 - \mathrm {e}^{-\frac {t}{\tau }}\right ) \cdot U_q \\ &= \frac {C \cdot R_2}{\tau } \cdot \mathrm {e}^{-\frac {t}{\tau }} \cdot U_q + \left (1 - \mathrm {e}^{-\frac {t}{\tau }}\right ) \cdot U_q \\ &= \frac {R_2}{R_1 + R_2} \cdot \mathrm {e}^{-\frac {t}{\tau }} \cdot U_q + \left (1 - \mathrm {e}^{-\frac {t}{\tau }}\right ) \cdot U_q \\ &= \left ( 1 + \frac {R_2}{R_1+R_2} \cdot \mathrm {e}^{-\frac {t}{\tau }} - \mathrm {e}^{-\frac {t}{\tau }} \right ) \cdot U_q \\ &= \left ( 1 - \frac {R_1}{R_1+R_2} \cdot \mathrm {e}^{-\frac {t}{\tau }} \right ) \cdot U_q \end {align*}

Skizze für $u_C$, $u_2$ und $u_{R_2}$. \begin {align*} u_{R_2}(0^-) &= u_2(0^-) = 0 \\ u_{R_2}(0^+) &= u_2(0^+) = \frac {R_2}{R_1+R_2} \cdot U_q \end {align*}

2 Einschaltverhalten (DC) eines verlustbehafteten Kondensators

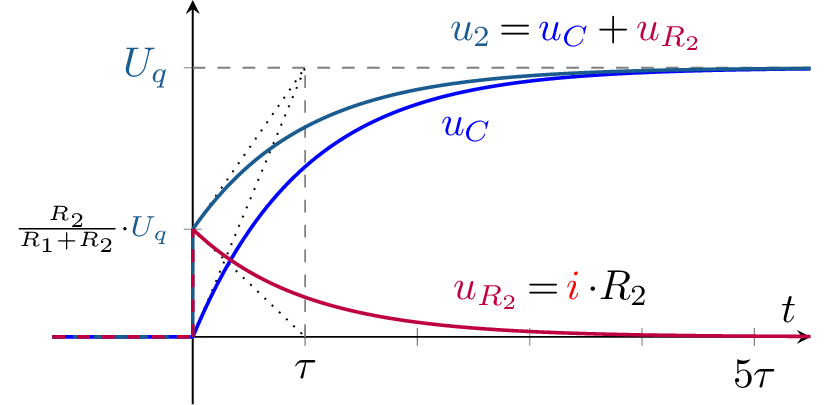
Das Einschaltverhalten der dargestellten Schaltung soll untersucht werden.

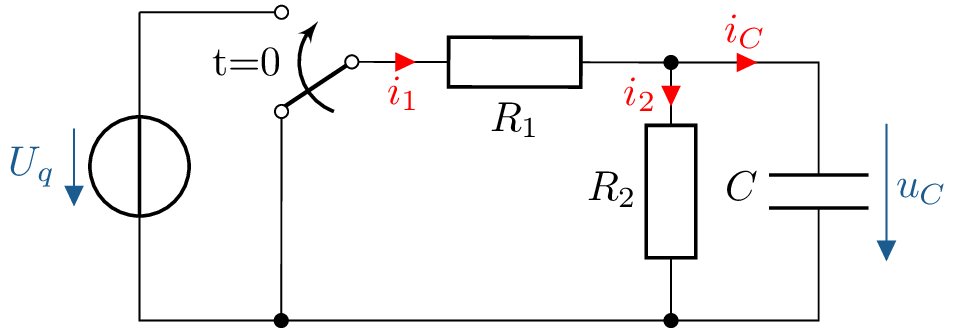
Zum Zeitpunkt $t = 0$ wird der Schalter umgelegt, so dass die Gleichspannung $U_q$ an der Schaltung anliegt. Die Kapazität ist vor dem Schaltzeitpunkt vollständig entladen.

Bestimmen Sie die Gleichung für die Spannung an der Kapazität $u_C(t)$ für $t \geq 0$.
Zeichnen Sie den zeitlichen Verlauf der Spannungen $u_C(t)$ und $u_{R1}(t)$ sowie des Stromes $i_C(t)$. Kennzeichnen Sie charakteristische Punkte.
Nach vollständigem Aufladen der Kapazität $C$ auf $U_{0}$ wird der Schalter wieder in Ausgangsposition gebracht. Wie lange braucht die Kapazität $C$, um auf $10\,\%$ der Spannung $U_{0}$ zu entladen?
Die Kapazität wird wie in c) entladen, allerdings mit offenem Schalter (Leerlauf). Wie lange dauert der Entladevorgang (von $U_0$ bis $10\,\%\cdot U_0$)? Vergleichen Sie die Dauer mit der aus c).

a) ESB ($t \geq 0$): $U_q$ an Schaltung: $R_1$ in Serie mit Parallelschaltung aus $R_2$ und $C$.

1. DGL aufstellen für $u_C$ ($t \geq 0$) \begin {align*} u_{R1} + u_C &= U_q & u_{R_1} &= R_1 \cdot i_{R1}\\ R_1 \cdot i_{R1} + u_C &= U_q & i_{R1} &= i_{R2} + i_C\\ R_1 \cdot (i_C + i_{R2}) + u_C &= U_q & i_C &= C \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C \qquad i_{R2} = \frac {u_C}{R_2}\\ C \cdot R_1 \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C + \frac {R_1}{R_2} \cdot u_C + u_C &= U_q &&\Big | \cdot R_2\\ C \cdot R_1 \cdot R_2 \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C + \left (R_1 + R_2 \right ) \cdot u_C &= U_q \cdot R_2 &&\Big | : (R_1+R_2)\\ \underbrace {C \cdot \frac {R_1 \cdot R_2}{R_1+R_2}}_{\tau } \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C + u_C &= U_q \cdot \frac {R_2}{R_1+R_2} \end {align*}

2. Homogene Lösung und 3. Partikuläre Lösung ($t \to \infty $) \begin {align*} u_{C,h} &= K \cdot \mathrm {e}^{\lambda t} = K \cdot \mathrm {e}^{-\frac {t}{\tau }} & \tau &= C \cdot \frac {R_1 \cdot R_2}{R_1+R_2} \\[2pt] u_{C,p} &= U_q \cdot \frac {R_2}{R_1+R_2} & &\text {$C$ entspricht Leerlauf} \end {align*}

4. Überlagerung und 5. Konstante $K$ bestimmen \begin {align*} u_C(t) = u_{C,h} + u_{C,p} &= K \cdot \mathrm {e}^{-\frac {t}{\tau }} + U_q \cdot \frac {R_2}{R_1+R_2} \\ u_C(0) &= K \cdot \cancel {\mathrm {e}^{0}} + U_q \cdot \frac {R_2}{R_1+R_2} \overset {!}{=} 0 & \Rightarrow K &= -U_q \cdot \frac {R_2}{R_1+R_2} \\ u_C(t) &= U_q \cdot \frac {R_2}{R_1+R_2} \cdot \left ( 1 - \mathrm {e}^{-\frac {t}{\tau }} \right ) \end {align*}

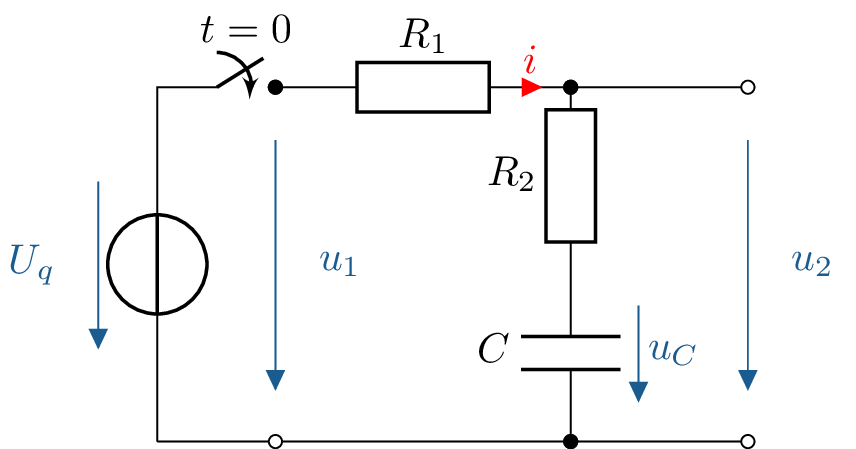
b) Skizze $u_C(t)$, $u_{R_1}$ und $i_C$ mit $u_C(t)$ aus a): \begin {align*} u_{R1}(t) &= U_q - u_C(t) \\ &= U_q - U_q \cdot \frac {R_2}{R_1+R_2} \cdot \left ( 1 - \mathrm {e}^{-\frac {t}{\tau }} \right ) \\ &= U_q \cdot \frac {R_1}{R_1+R_2} + U_q \cdot \frac {R_2}{R_1+R_2} \cdot \mathrm {e}^{-\frac {t}{\tau }} \\[4pt] i_C(t) &= C \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C(t) \\ &= C \cdot U_q \cdot \frac {R_2}{R_1+R_2} \cdot \frac {1}{\tau } \cdot \mathrm {e}^{-\frac {t}{\tau }} \\ &= U_q \cdot \frac {\cancel {C} \cdot \cancel {R_2}}{\cancel {R_1+R_2}} \cdot \frac {\cancel {R_1+R_2}}{\cancel {C} \cdot R_1 \cdot \cancel {R_2}} \cdot \mathrm {e}^{-\frac {t}{\tau }}\\ &= \frac {U_q}{R_1} \cdot \mathrm {e}^{-\frac {t}{\tau }} \end {align*}

Zeitverläufe:

Entladen von $C$ über Parallelschaltung aus $R_1$ und $R_2$ für $t'\geq 0$ bis $U_0 \cdot 10\,\%$
Entlade-Zeitkonstante: $\tau _1= \tau = C \cdot \frac {R_1 \cdot R_2}{R_1+R_2}$: \begin {align*} u_C(t') = U_0 \cdot \mathrm {e}^{-\frac {t'}{\tau }} &\overset {!}{=} U_0 \cdot 10\,\% \\ \mathrm {e}^{-\frac {t'}{\tau }} &= \frac {1}{10} \\ -\frac {t'}{\tau } &= \ln \left (\frac {1}{10}\right ) = -\ln \left (10\right ) \\ t' &= \ln \left (10\right ) \cdot \tau \approx 2,3025 \cdot \tau \end {align*}
Entladen von $C$ über $R_2$, wenn Schalter öffnet (Leerlauf) für $t'\geq 0$ bis $U_0 \cdot 10\,\%$.
Lösung wie bei Aufgabe c) nur mit Entlade-Zeitkonstante $\tau _2 = R_2 \cdot C$.
Die Kapazität entlädt langsamer als in Aufgabe c) ($\tau _2 > \tau $), da $R_2 > R_1||R_2$.

3 Schaltverhalten einer RL-Serienschaltung

Das Schaltverhalten, der in der linken Abbildung dargestellten Schaltung, soll untersucht werden.
Der Verlauf der Spannung $u_1(t)$ ist in der rechten Abbildung dargestellt.

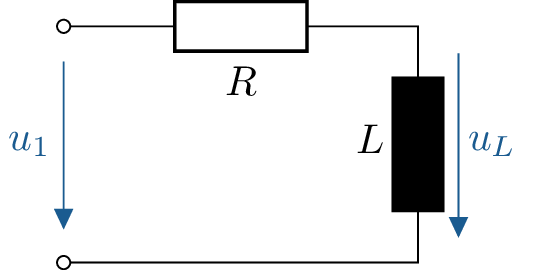
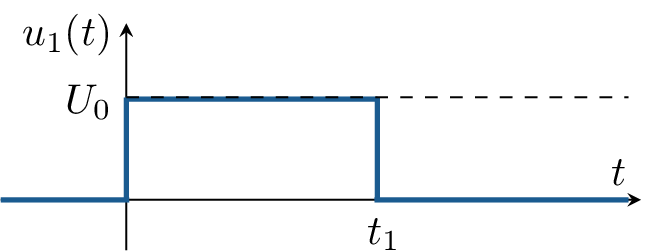
Vor dem Zeitpunkt $t=0$ war die Spannung $u_1 = 0$, so dass zum Zeitpunkt $t=0$ keine Energie in der Spule gespeichert ist. Weiterhin gilt $t_1 \gg 5\tau $.

Es soll der Aufladevorgang ($0<t<t_1$) betrachtet werden. Es gilt $\tau = 1\,ms$ und $R=100\,\Omega $. Wie groß ist die Induktivität $L$?
Es soll weiterhin der Aufladevorgang ($0<t<t_1$) betrachtet werden. Gegeben ist nun die Spannung $U_0=1\,kV$. Wie groß ist der Strom durch die Spule $i_L$ zum Zeitpunkt $t=3\tau $?
Es wird weiterhin der Aufladevorgang betrachtet. Nun gilt jedoch: $R = 5\,\Omega $, $L=100\,mH$ und $U_0=2,8\,kV$.
- Nach welcher Zeit $t_0$ ist der Einschwingvorgang abgeschlossen?
- Wie groß sind der Spulenstrom $i_L$ und die Spulenspannung $u_L$ nach $t=50\,ms$?
Nun soll der Entladevorgang ($t>t_1$) betrachtet werden. Es gelten die Werte aus dem vorangehenden Aufgabenteil. Wie groß sind Spulenstrom $i_L$ und Spulenspannung $u_L$ nach $t=t_1 +50\,ms$?
Zeichnen Sie die zeitlichen Verläufe der Spulenspannung $u_L$, des Stromes $i_L$, sowie der Spannung $u_R$. Kennzeichnen Sie die Zeitkonstante $\tau $, sowie weitere charakteristische Punkte. Nehmen Sie an $t_1 = 120\,ms$.

\begin {align*} \text {DGL (allgemein):}&& \frac {L}{R}\cdot \frac {\mathrm {d}}{\mathrm {d}t}\, i &= \frac {U_1}{R_1} \text {(Einschalten)}\\ \text {Lösungsansatz:}&& i &= \frac {U_0}{R}\cdot (1-e^{-\frac {t}{\tau }})\text {mit}\tau =\frac {L}{R} \end {align*}

a) Induktivität berechnen.

$\tau =\frac {L}{R}$ $L=\tau \cdot R=1\,ms\cdot 100\,\Omega =0,1\,H$

b) Aufladevorgang, Spulenstrom $i_L$ zum Zeitpunkt $t=3\tau $.\begin {align*} i(t=3\cdot \tau ) &= \frac {U_0}{R}(1-e^{-\frac {t}{\tau }})\\ &=\frac {1\,kV}{100\,\Omega }\cdot (1-e^{-3}) = 10\,A\cdot 0,95\\ &=9,5\,A \end {align*}

c) Zeit bis zum Abschluss des Einschwingvorgangs, Spulen -Strom und -Spannung nach $50\,ms$.\begin {align*} \tau &=\frac {L}{R}=\frac {0,1\,H}{5\,\Omega }=0,02\,s=20\,ms\\\\ i(t=50\,ms)&=\frac {U_0}{R}\cdot (1-e^{-\frac {t}{\tau }})\\ &=\frac {2,8\,kV}{5\,\Omega }\cdot (1-e^{-\frac {50\,ms}{20\,ms}})\\ &=0,56\,kA\cdot (0,918)=0,514\,kA\\\\ u_L&=L\cdot \frac {\mathrm {d}}{\mathrm {d}t} i_L = \frac {L}{R}\cdot U_0 \cdot (-\frac {1}{\tau })\cdot (-e^{-\frac {t}{\tau }})\\ &= U_0\cdot e^{-\frac {t}{\tau }}\\\\ u_L(t=50\,ms)&=2,8\,kV\cdot e^{-\frac {50\,ms}{20\,ms}}=229,8\,V\\ t_0&=5\cdot \tau =5\cdot 20\,ms=100\,ms \end {align*}

d) Entladevorgang, Spulen -Strom und -Spannung nach $t = t_1 + 50\,ms$.\begin {align*} \text {DGL (Entladevorgang):}&& \frac {L}{R}\cdot \frac {\mathrm {d}}{\mathrm {d}t}\, i+i &=0\\ \text {Lösungsansatz:}&& i &= \frac {U_0}{R}\cdot e^{-\frac {t}{\tau }}\text {mit}\tau =\frac {L}{R}\\ \end {align*}

\begin {align*} u_L&=L\cdot \frac {\mathrm {d}}{\mathrm {d}t} i = \frac {L}{R}\cdot u_0\cdot (-\frac {1}{\tau })\cdot e^{-\frac {t}{\tau }}\\ &=-U_0\cdot e^{-\frac {t}{\tau }}\\ i(50\,ms)&=\frac {2,8\,kV}{5\Omega }\cdot e^{-\frac {50\,ms}{20\,ms}}=46\,A\\ u_L(50\,ms)&=-2,8\,kV\cdot e^{-\frac {50\,ms}{20\,ms}}=-230\,V \end {align*}

e) Zeitliche Verläufe von $u_L, i_L, u_R$.

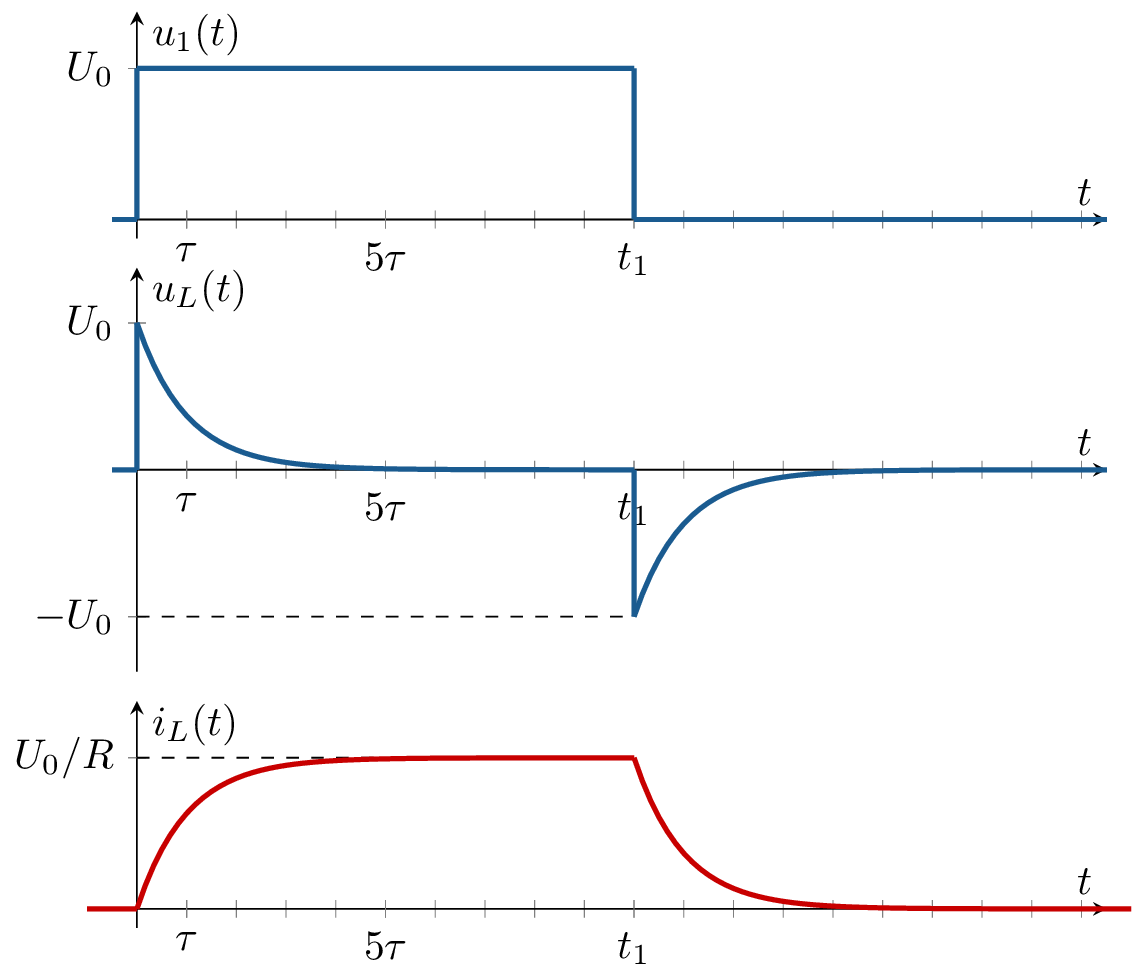
1 Einschaltverhalten eines RC-Übertragungsgliedes

2 Einschaltverhalten (DC) eines verlustbehafteten Kondensators

3 Schaltverhalten einer RL-Serienschaltung

In Module 12

Additional materials