Sprache wählen Icon

Einfache Kondensatornetzwerke

Wie Widerstände lassen sich auch Kapazitäten zu Netzwerken zusammenschließen. Die einfachen Grundschaltungen, welche wiederum zu beliebig komplexen Netzwerken zusammengeschaltet werden können, werden nachfolgend vorgestellt.

1 Parallelschaltung von Kapazitäten

Sind in einer Schaltung mehrere Kapazitäten parallel zueinander geschaltet, lassen sie sich zu einer Gesamtkapazität zusammenfasssen (siehe Abbildung 1).

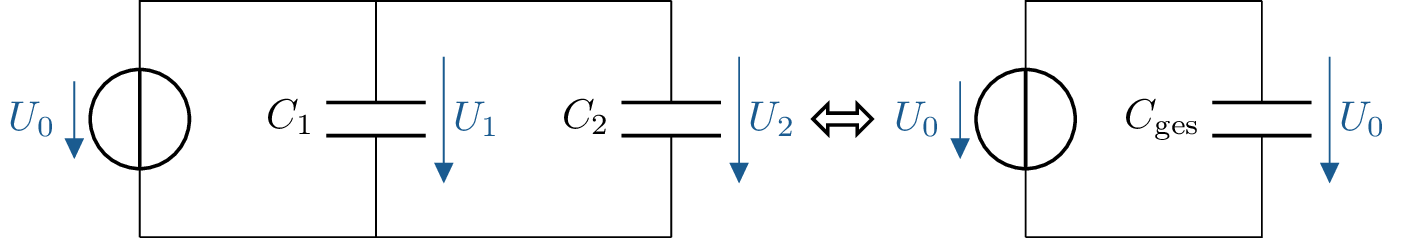
Schematische Darstellung zweier parallel geschalteter Kondensatoren C1 und C2, die an eine gemeinsame Spannungsquelle U0 angeschlossen sind. Beide Kondensatoren besitzen die gleiche Spannung U1 = U2 = U0. Rechts daneben ist das äquivalente Ersatzschaltbild gezeigt, bei dem die beiden Kondensatoren durch eine einzige Gesamtkapazität Cges ersetzt wurden, die ebenfalls an die Spannung U0 angeschlossen ist. Ein Doppelpfeil zwischen beiden Schaltungen verdeutlicht die Gleichwertigkeit der Darstellungen.

Abbildung 1: Zusammenfassen von zwei parallel geschalteten Kapazitäten \(C_1\) und \(C_2\) zu einer Gesamtkapazität \(C_\mathrm {ges}\)

Dabei liegt an allen Einzelkapazitäten die gleiche Spannung an:

\begin {equation*} U_0 = U_1 = U_2 \end {equation*}

Die Ladung, welche auf jedem der Einzelkondensatoren gespeichert ist, kann wie folgt bestimmt werden:

\begin {equation*} Q_k = C_k \cdot U_0 \end {equation*}

Die Gesamtladung \(C_\mathrm {ges}\) auf dem in Abbildung 1 Ersatzschaltbild entsprechend mit

\begin {equation*} Q_\mathrm {ges} = C_\mathrm {ges} \cdot U_0 \end {equation*}

Die Gesamtladung setzt sich aus der Summe der Einzelladungen zusammen:

\begin {equation*} Q_\mathrm {ges} = Q_1 + Q_2 = C_1 \cdot U_0 + C_2 \cdot U_0 \end {equation*}

\begin {equation*} Q_\mathrm {ges} = (C_1 + C_2) \cdot U_0 \end {equation*}

Ein Quotientenvergleich mit der ursprünglichen Berechnung der Gesamtladung \(Q_\mathrm {ges}\) zeigt nun:

\begin {equation*} \rightarrow C_1 + C_2 = C_\mathrm {ges} \end {equation*}

Auch für beliebig viele parallelgeschaltete Kapazitäten gilt, dass die Summe der Einzelkapazitäten die Gesamtkapazität ergibt:

Merke: Gesamtkapazität einer Parallelschaltung

\begin {equation*} C_\mathrm {ges} = \sum _{k=1}^{n} C_k \end {equation*}

2 Reihenschaltung von Kapazitäten

Bei der Reihenschaltung von Kapazitäten teilt sich die gesamte an den Eingangsanschlüssen anliegende Spannung \(U_\mathrm {0}\) in die Teilspannungen \(U_k\) an den einzelnen Kapazitäten auf (Abbildung 2).

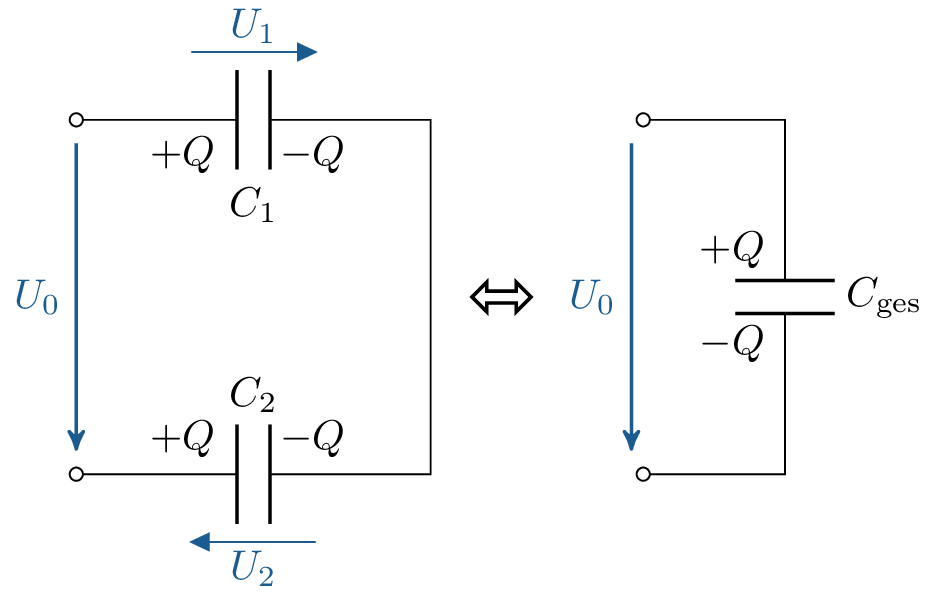
Schematische Darstellung zweier in Reihe geschalteter Kondensatoren C1 und C2 mit jeweils gleicher Ladung Q und der Spannung U1 beziehungsweise U2. Die Gesamtspannung U0 verteilt sich auf beide Kondensatoren. Rechts daneben ist das äquivalente Ersatzschaltbild mit einer Gesamtkapazität Cges dargestellt, die zwischen denselben Anschlüssen liegt und die Gesamtspannung U0 trägt. Ein Doppelpfeil zwischen den beiden Schaltungen zeigt die Gleichwertigkeit der Darstellungen.

Abbildung 2: Zusammenfassen von zwei in Reihe geschalteten Kapazitäten \(C_1\) und \(C_2\) zu einer Gesamtkapazität \(C_\mathrm {ges}\)

Auf den jeweils mit den Anschlussklemmen verbundenen Kondensatorplatten wird eine Ladung \(\pm \, Q\) aufgeprägt. Beide Platten des selben Kondensators haben stets betragsgleiche Ladungen, was dazu führt, dass beide Kondensatoren an den Anschlussklemmen der Reihenschaltung auf beiden Platten die Ladung \(\pm \, Q\) haben. Die äußere Platte des jeweils nächsten angeschlossenen Kondensators muss betragsmäßig identisch mit umgekehrten Vorzeichen geladen sein, da aus der ursprünglich elektrisch neutralen Verbindung keine Ladungsträger entweichen oder hinzugefügt werden können. Diesem Schema folgend besitzen alle Kondensatoren einer Reihenschaltung die gleiche Ladung \(Q\).

Ausgehend von der Kondensator-Grundgleichung \(Q = C \cdot U\) ergibt sich für die Teilspannungen, welche an den in Abbildung 2 gezeigten Kondensatoren abfallen:

\begin {equation*} U_1 = \frac {Q}{C_1}, U_2 = \frac {Q}{C_2} \end {equation*}

Eingesetzt in das Ergebnis des Maschenumlaufs der Ausgangsschaltung ergibt sich:

\begin {equation*} U_0 = U_1 + U_2 = \left ( \frac {1}{C_1} + \frac {1}{C_2} \right ) \cdot Q \end {equation*}

Die Spannung \(U_0\) im Ersatzschaltbild kann wie folgt berechnet werden:

\begin {equation*} U_0 = \frac {1}{C_\mathrm {ges}} \cdot Q \end {equation*}

Ein Quotientenvergleich offenbart:

\begin {equation*} \frac {1}{C_1} + \frac {1}{C_2} = \frac {1}{C_\mathrm {ges}} \end {equation*}

Allgemein gilt für eine Reihenschaltung aus beliebig vielen Kondensatoren:

Merke: Gesamtkapazität einer Reihenschaltung:

\begin {equation} \frac {1}{C_\mathrm {ges}} = \sum _{i = 1}^{n} \frac {1}{C_i} \end {equation}

Bei zwei in Reihe geschalteten Kondensatoren kann die Gesamtkapazität \(C_\mathrm {ges}\) analog zur Parallelschaltung von Widerständen auch mit folgendem Ausdruck ermittelt werden:

\begin {equation*} C_\mathrm {ges} = \frac {C_1 \cdot C_2}{C_1 + C_2} \end {equation*}

3 Spannungsteiler an Kapazitäten

Ähnlich wie beim Spannungsteiler an in zwei in Reihe geschalteten Widerständen lässt sich auch das Verhältnis der Teilspannung an zwei in Reihe geschalteten, identisch geladenen Kondensatoren ermitteln (siehe Abbildung 3).

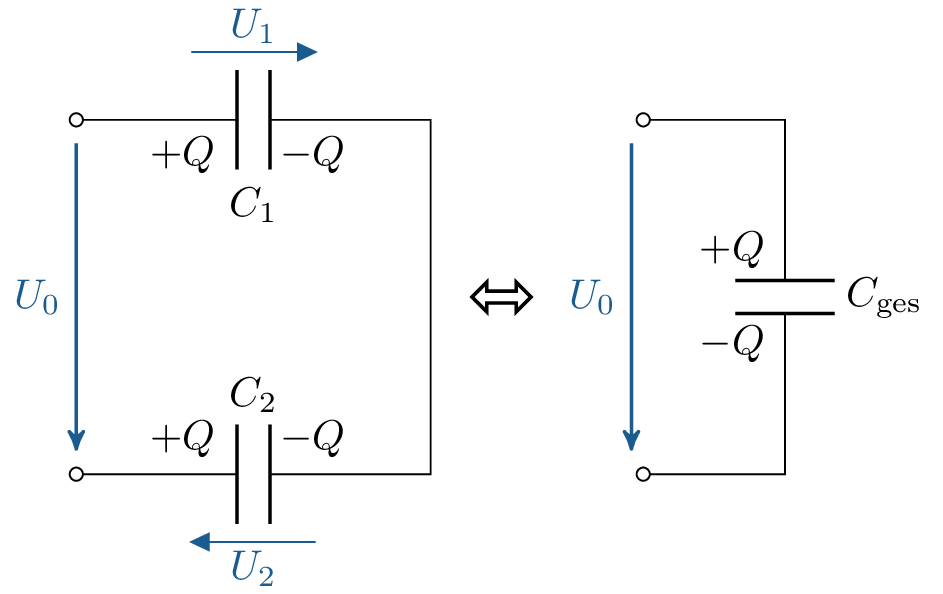
Darstellung eines Spannungsteilers mit zwei in Reihe geschalteten Kondensatoren C1 und C2, die jeweils entgegengesetzte Ladungen +Q und -Q tragen. Die Spannungen U1 und U2 liegen über den einzelnen Kondensatoren, während die Gesamtspannung U0 beide umfasst. Rechts daneben ist das äquivalente Ersatzschaltbild mit einer Gesamtkapazität Cges und derselben Spannung U0 dargestellt.

Abbildung 3: Spannungsteiler an einer Reihenschaltung von zwei Kapazitäten (links) sowie Ersatzschaltbild nach Zusammenfassen der Kapazitäten zu \(C_\mathrm {ges}\)

Die Spannung \(U_1\) kann wie folgt ermittelt werden:

\begin {equation*} U_1 = \frac {Q}{C_1} \end {equation*}

Die Ladung \(Q\) ist unbekannt, jedoch sowohl bei beiden Kondensatoren \(C_1\) und \(C_2\) als auch in der Ersatzschaltung bei \(C_\mathrm {ges}\) identisch:

\begin {equation*} Q = C_\mathrm {ges} \cdot U_0 = \frac {C_1 \cdot C_2}{C_1 + C_2} \cdot U_0 \end {equation*}

Eingesetzt ergibt sich für \(U_1\):

\begin {equation*} U_1 = \frac {1}{\cancel {C_1}} \cdot \frac {\cancel {C_1} \cdot C_2}{C_1 + C_2} \cdot U_0 = U_0 \cdot \frac {C_2}{C_1 + C_2} \end {equation*}

Der Spannungsteiler für \(U_2\) berechnet sich analog:

Merke:

\begin {equation*} U_1 = \frac {C_2}{C_1 + C_2} \cdot U_0, U_2 = \frac {C_1}{C_1 + C_2} \cdot U_0 \end {equation*}

Expand
×

...