Der Transformator

Der Transformator ist eine ruhende elektrische Maschine und dient der Energiewandlung von elektrischer Energie über den magnetischen Kreis zurück in elektrische Energie, wobei insbesondere die Spannungshöhe gewandelt wird. Transformatoren gibt es in verschiedenen Ausführungen und Leistungsklassen von wenigen Watt (Abbildung 2) bis in den hohen Megawattbereich (Abbildung 1).

In der öffentlichen Energieversorgung wird die von Kraftwerken erzeugte Energie auf eine höhere Spannung transformiert, um sie über weite Strecken transportieren zu können. Die Übertragungsverluste sinken mit höherer Spannung und damit bei gleicher Leistung sinkendem Strom quadratisch (Gleichung 1 im Dreiphasenwechselstrom).

\begin {equation} P_\mathrm {v} = 3\cdot R_\mathrm {L}\cdot I_\mathrm {L}^2\label {GlVerlustleistung} \end {equation}

Die übertragene Leistung im Dreiphasenwechselstrom beträgt:

\begin {equation} \underline {S}_\mathrm {N} = \sqrt {3}\cdot \underline {U}_\mathrm {N} \cdot \underline {I}_\mathrm {L}^\ast \end {equation}

Die Verluste sind damit proportional zu \(\frac {1}{\underline {U}_\mathrm {N}^2}\)

Ein Transformator macht dadurch erst eine flächendeckende Energieversorgung möglich, da Kraftwerke auch verbraucherfern positioniert werden können.

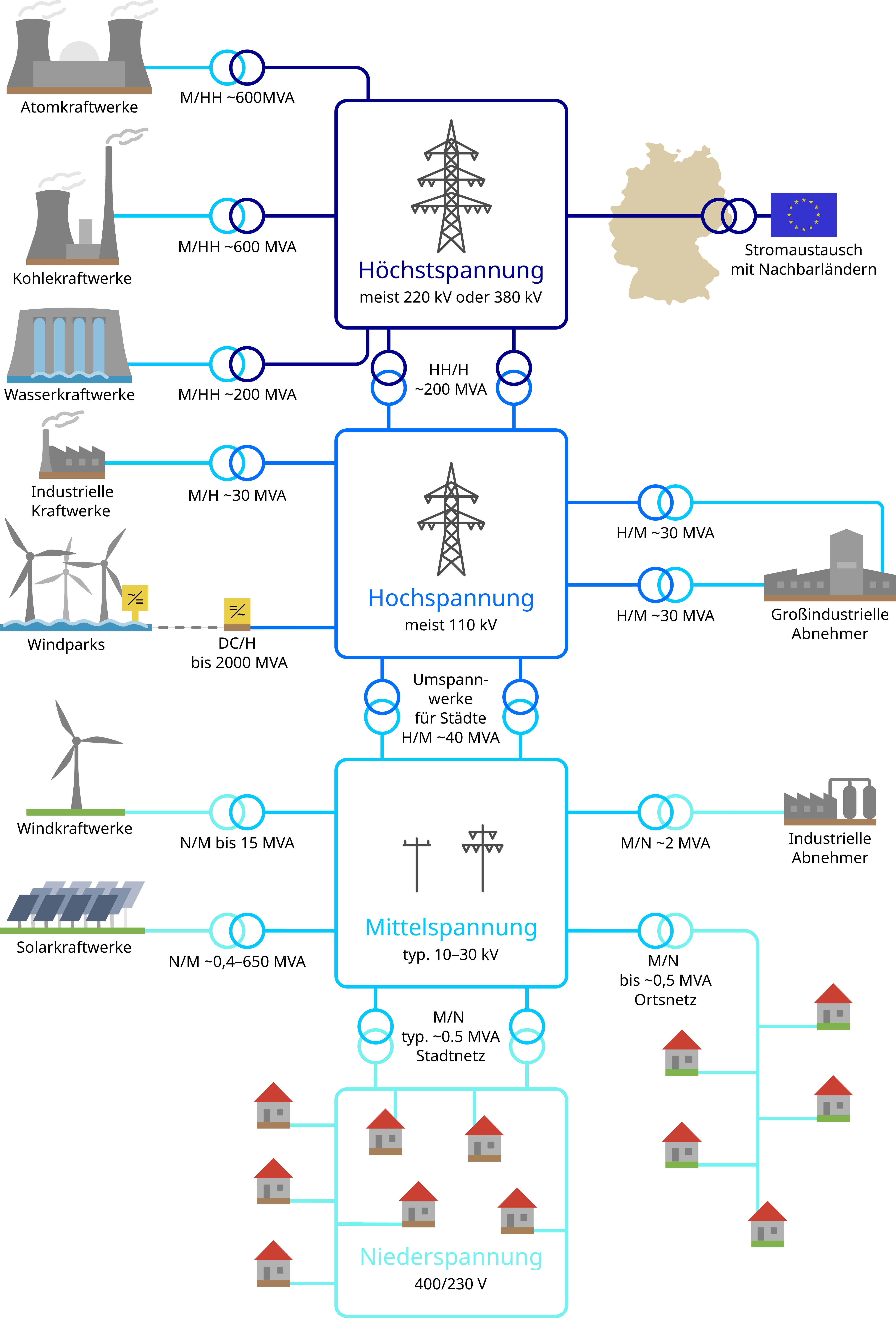
In Energieversorgungsnetzen (siehe Abbildung 3) gibt es mehrere Spannungsebenen. Die Höchstspannungsebene, die in Europa überwiegend \(380\,\)kV beträgt, dient als Übertragungsnetz zum Transport elektrischer Leistung über weitere Strecken, also mehrere hundert Kilometer auch über Ländergrenzen hinweg. Große Kraftwerke sind dort direkt angekoppelt. Die Hochspannungsebene (\(110\,\)kV oder \(220\,\)kV) nennt sich Verteilnetz und dient der Ankopplung von Städten und großen Industrien. Die Mittelspannungsebene (\(5-35\,\)kV) sorgt für die Ankopplung der Ortznetztransformatoren zur Versorgung von einzelnen Straßenzügen. Während die höheren Spannungsebenen normalerweise mit Freileitungen ausgeführt sind, ist das Mittelspannungsnetz überwiegend mit Erdkabeln realisiert. Im ländlichen Bereich werden aber auch hier Freileitungen eingesetzt.

Das Stromnetz ist in mehrere Spannungsebenen unterteilt, die den Transport und die Verteilung der Energie ermöglichen.

1 Prinzip des Transformators

Um das Prinzip des Transformators zu erörtern, starten wir mit einem vollständig verlustfreien, idealen Transformator. An der Primärspule wird eine sinusförmige (eigentlich Kosinusförmig, was aber die gleiche Form ist und nur einer Phasenverschiebung von \(90^\circ \) entspricht) Spannung \(\underline {U}_1\) angelegt. Der zeitliche Verlauf von \(\underline {U}_1\) entspricht \(u\) in Gleichung 3.

\begin {equation} u = \hat {U}\cdot \cos (\omega t)\label {GlSpannung1} \end {equation}

Diese Spannung bewirkt entsprechend der Umkehrung des Induktionsgesetzs (Gleichung 4) einen wechselnden magnetischen Fluss. \begin {equation} u = -N\cdot \frac {\mathrm {d}\varPhi }{\mathrm {d}t}\label {GlInduktionsgesetz} \end {equation}

Die Form des magnetischen Flusses ist bei sinusförmiger Spannungsform ebenfalls sinusförmig, da das Integral eines Kosinus der Sinus ist. Der Effektivwert des magnetischen Flusses kann daher durch Gleichung 5 dargestellt werden, indem das Induktionsgesetz nach \(\varPhi \) aufgelöst wird und der Effektivwert gebildet wird. Der Sinus und damit die zeitliche Abhängigkeit fällt dadurch weg. \begin {equation} \varPhi = \frac {\sqrt {2}\cdot \underline {U}_1}{2\pi \cdot N_1 \cdot f}\label {GlMagnetischerFluss} \end {equation}

Die Flussrichtung des Magnetfelds bewegt sich stets gemäß der „rechten Handregel“ (siehe Modul 4), in diesem Beispiel gegen den Uhrzeigersinn. Der so erzeugte magnetische Fluss induziert wiederum an der Sekundärspule des Transformators, die optimalerweise mit dem gleichen Fluss \(\varPhi \) durchdrungen wird, eine Spannung \(\underline {U}_2\), die sich auch nach dem Induktionsgesetz (Gleichung 4) berechnen lässt. \begin {equation} u_2 = -N_2\cdot \frac {\mathrm {d}\varPhi }{\mathrm {d}t}\tag {\ref {GlInduktionsgesetz}} \end {equation}

Die angelegte Primärspannung \(\underline {U}_1\) und die Sekundärspannung \(\underline {U}_2\) können in ein Verhältnis gesetzt werden (Gleichung 7). Die Änderungsrate des magnetischen Flusses \(\varPhi \) kürzt sich dadurch heraus, es bleiben nur noch die Windungszahlen der Primärseite \(N_1\) und der Sekundärseite \(N_2\) übrig. Dieses Verhältnis wird Übersetzungsverhältnis ü (Gleichung 7) genannt. Ist das Übersetzungsverhältnis ü größer als Eins wird die Spannung herabgesetzt (Spannungsabwärtstransformator). Ist das Übersetzungsverhältnis ü kleiner als Eins, wird die Spannung erhöht (Spannungsaufwärtstransformator). Da der Transformator in beide Richtungen eingesetzt werden kann, wird in den technischen Daten immer ein Übersetzungsverhältnis größer oder gleich Eins angegeben. \begin {equation} \frac {\underline {U}_1}{\underline {U}_2} = \frac {-N_1\cdot \frac {\mathrm {d}\varPhi }{\mathrm {d}t}}{-N_2\cdot \frac {\mathrm {d}\varPhi }{\mathrm {d}t}} = \frac {N_1}{N_2} = \textit {ü} \label {Gluebertragung} \\ \end {equation}

\begin {align} \textit {ü} < 1 &\rightarrow \text {Spannung hoch}\nonumber \\ \textit {ü} > 1 &\rightarrow \text {Spannung runter}\nonumber \end {align}

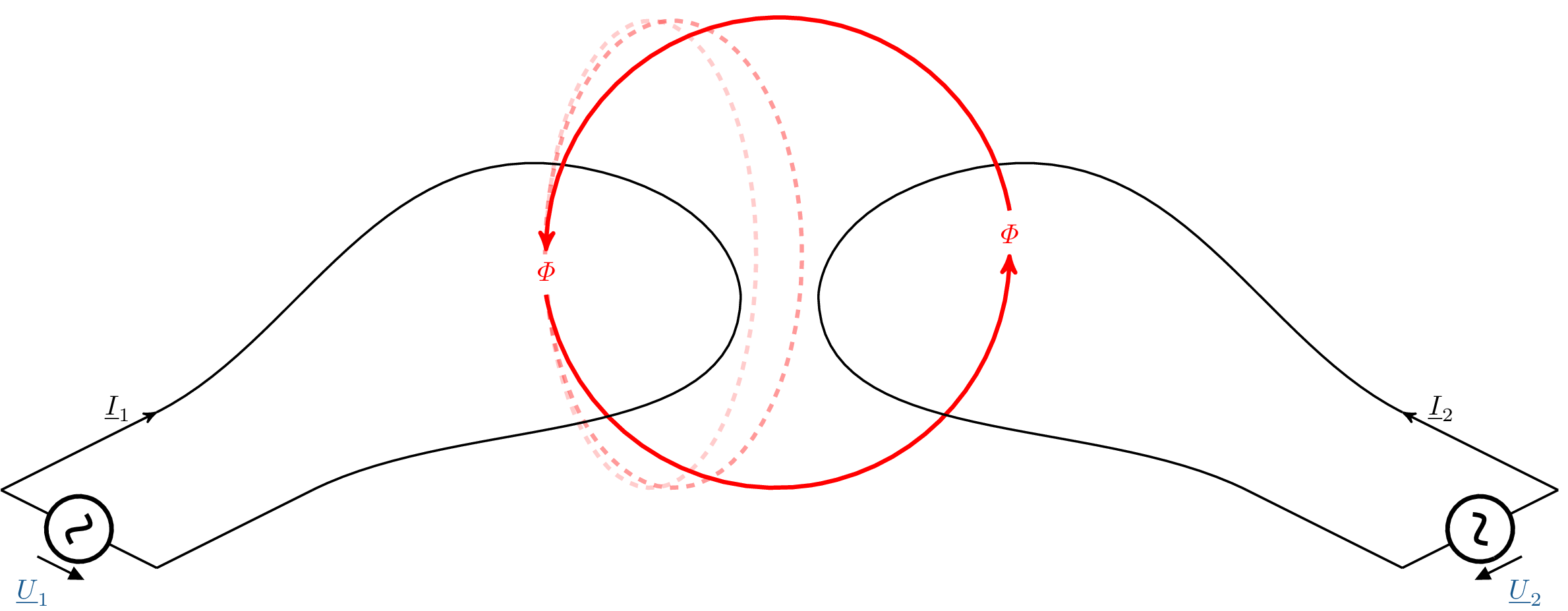
Bei einem realen Transformator durchdringt nicht der komplette magnetische Fluss, der durch die Primärwicklung erzeugt wird, auch die Sekundärseite (in Abbildung 4 rot gestrichelt dargestellt). Diese Verluste werden Streufluss genannt und werden im Ersatzschaltbild durch die Streuinduktivität dargestellt. Daher ist die reale Sekundärspannung kleiner als die hier berechnete ideale Sekundärspannung.

2 Aufbau des Transformators

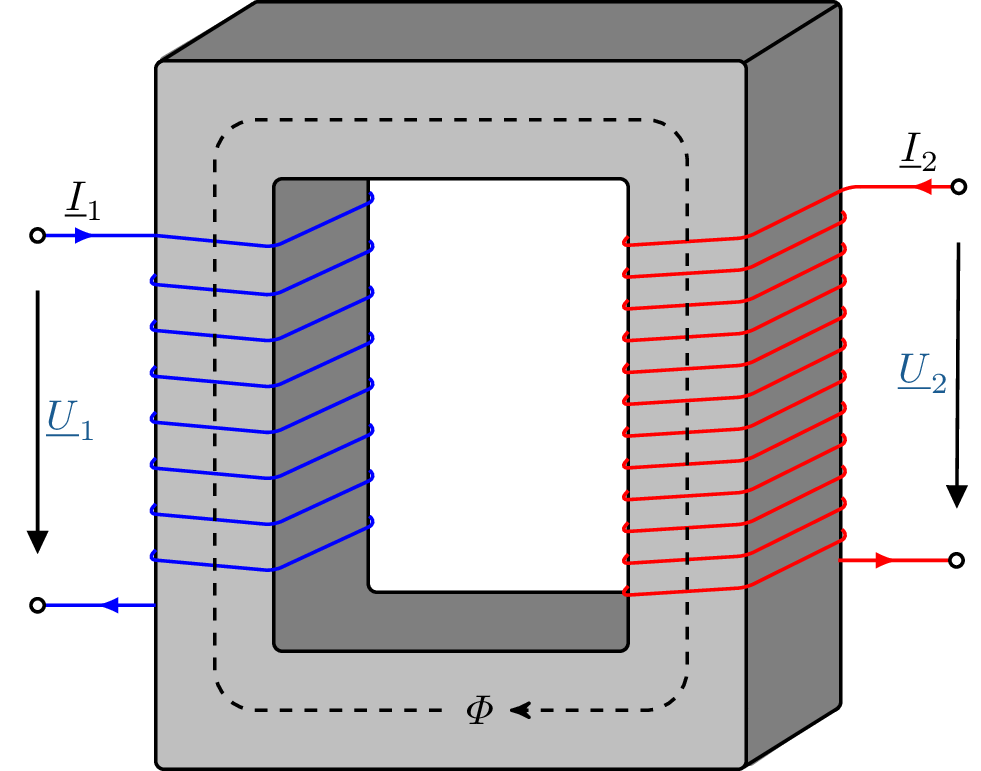
Vereinfacht dargestellt besteht der Transformator aus zwei Spulen, die mittels eines magnetisch leitenden Kerns miteinander gekoppelt werden (siehe Abbildung 5). Der Kern besteht aus einem ferromagnetischen Material. Durch seine hohe Permeabilität hat das ferromagnetische Material die Fähigkeit, den magnetischen Fluss möglichst effizient zwischen zwei Spulen zu leiten (siehe Modul 6). Effekte wie die Hysterese und Wirbelstromverluste stören jedoch den widerstandslosen Fluss. Diese Effekte werden als Eisenverluste bezeichnet.

Die Spulen sind um den magnetischen Leiter gewickelt. Wie oben erwähnt, bestimmen die Windungszahlen das Übersetzungsverhältnis der Spannung (Gleichung 7). Sie bestehen aus elektrisch gut leitenden Drähten wie Kupfer. Auch diese weisen in der Realität Widerstandsverluste auf, die auch Kupferverluste genannt werden.

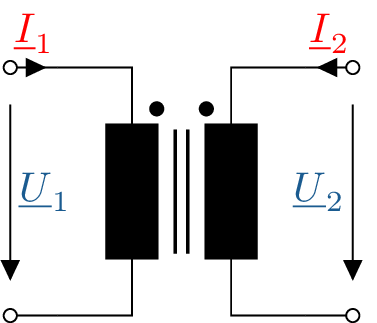
In dem Schaltbild des idealen Transformators werden die magnetisch gekoppelten Spulen als nebeneinanderstehende, schwarz ausgefüllte Rechtecke dargestellt (siehe Abbildung 6). Die zwei Striche zwischen den Spulen weisen darauf hin, dass diese mittels eines durchgehenden magnetisch leitenden Kerns verbunden sind. Die Punkte an den jeweiligen Spulen geben Aufschluss über die Führung der Wicklung. Sie können sich unten oder oben befinden. Liegen sie dabei auf der gleichen Höhe, ist die Phasenlage der beiden Spulen gleich. Liegen diese auf unterschiedlichen Höhen, bedeutet dies einen umgekehrten Wicklungssinn und dadurch eine Phasenverschiebung von \(180^\circ \).

3 Ersatzschaltbild

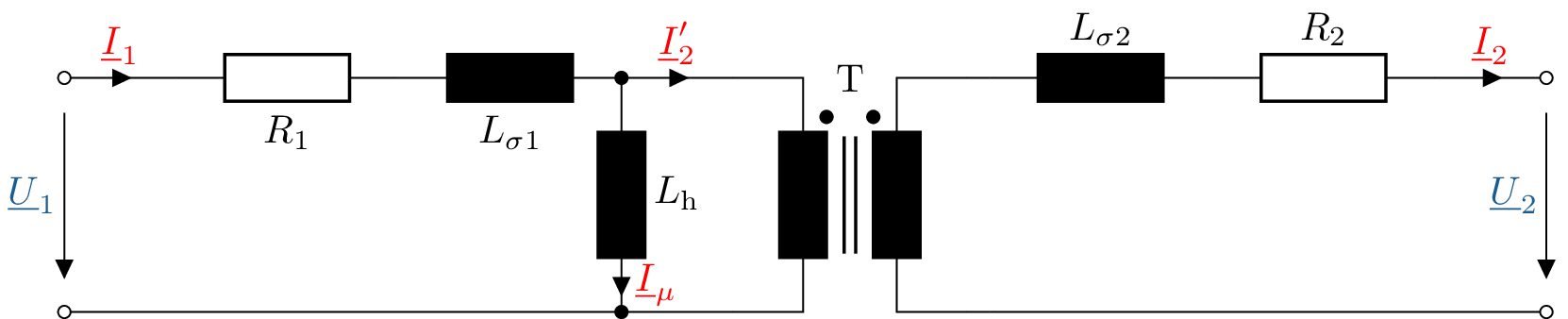
Zum besseren Verständnis wird das Ersatzschaltbild des realen Transformators (Abbildung 7) zunächst funktionsgetreu als galvanisch getrenntes System mit einem Primär- und einem Sekundärstromkreis dargestellt. Im Vergleich zum idealen Transformator ist dieses Ersatzschaltbild um die zuvor beschriebenen Verluste erweitert. Der magnetische Kreis wird mit der Hauptinduktivität \(L_h\) und den Streuinduktivitäten \(L_{\sigma 1}\) und \(L_{\sigma 2}\) in einen elektrischen Kreis transformiert. Die zuvor beschriebenen Kupferverluste in der Primär- und Sekundärspule werden durch die Widerstände \(R_1\) und \(R_2\) repräsentiert. Die Größe \(\underline {I}\mu \) steht für den Magnetisierungsstrom und beschreibt jene Komponente des Leerlaufstroms, die erforderlich ist, um den magnetischen Kern des Transformators zu erregen. Die Eisenverluste werden aus Gründen der Vereinfachung in diesem Beispiel außer acht gelassen. Wenn sie berücksichtigt werden sollen, werden die Eisenverluste durch eine Parallelschaltung eines Widerstandes zur Hauptinduktivität dargestellt.

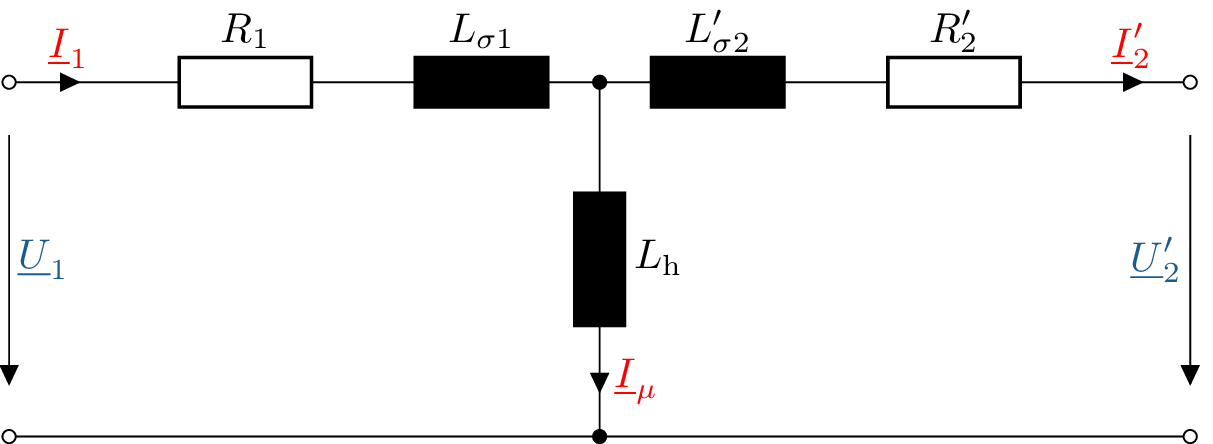
Anschließend wird in dem T-Ersatzschaltbild des Transformators (Abbildung 8) unterstellt, dass keine galvanische Trennung zwischen Primär- und Sekundärseite besteht, obwohl dies in der Realität natürlich der Fall ist. Dieser Schritt ermöglicht die Umrechnung der Größen der Sekundärseite auf die Primärseite und die Anwendung der aus Modul 4 bekannten Rechenregeln. Die Umrechnungsgrößen werden als gestrichne Größen, in diesem Beispiel als \(\underline {U}^\prime _2\), \(\underline {I}^\prime _2\), \({R}^\prime _2\) und \({L}^\prime _{\sigma 2}\), gekennzeichnet.

Für die Umrechung der Spannung auf die Primärseite wird die Spannung \(\underline {U}^\prime _2\) mit dem Übersetzungsverhältnis multipliziert (Gleichung ??). Zur Berechnung des eingehenden Stroms \(\underline {I}_1\) wird der Strom \(\underline {I}_2\) mit dem umgekehrten Übersetzungsverhältnis multipliziert und anschließend mit dem Magnetisierungsstrom \(\underline {I}_\mu \) addiert (Gleichung ??). \begin {align} \underline {U}_1 = \underline {U}^\prime _2 &= \frac {N_1}{N_2}\cdot \underline {U}_2 \label {Glspannungsumrechnung} \\ \underline {I}_1 = \underline {I}^\prime _2 + \underline {I}_\mu &= \frac {N_2}{N_1}\cdot \underline {I}_2 + \underline {I}_\mu \label {Glstromumrechnung} \end {align} Die auftretenden Verluste auf der Sekundärseite \(L_{\sigma 2}^\prime \) und \(R_2^\prime \) werden mit dem quadrierten Übersetzungsverhältnis auf die Primärseite umgerechnet (Gleichungen ?? und ??). \begin {align} L_{\sigma 2}^\prime &= \left (\frac {N_1}{N_2}\right )^2\cdot L_{\sigma 2} \label {Glstreuinduktivitätumrechnung} \\ R_2^\prime &= \left (\frac {N_1}{N_2}\right )^2\cdot R_2\label {Glwiderstandumrechnung} \end {align}