Handreichung
Diese Handreichung dient als offizieller Leitfaden zur Nutzung und Adaption der im Rahmen des Verbundprojekts „GET it digital“ entwickelten Lehr- und Lernmaterialien. Die Materialien wurden als Open Educational Resources (OER) konzipiert, um Lehrenden an Hochschulen ein didaktisch ausgereiftes und digitales Baukastensystem für die Grundlagen der Elektrotechnik (GET) bereitzustellen. Ziel ist es, die Qualität der Lehre zu steigern und Lehrenden eine effiziente Gestaltung ihrer Veranstaltungen zu ermöglichen.
Alle Materialien, einschließlich Skripte, Folien, Lernvideos, Moodle-Tests und Aufgabensammlungen, sind unter der Lizenz CC BY 4.0 lizenziert. Diese Lizenz erlaubt die freie Nutzung, Bearbeitung und Weiterverbreitung der Inhalte unter Nennung der Autorenschaft. Ausgenommen hiervon sind lediglich explizit gekennzeichnete Elemente und Logos.
Zielgruppe und Lernziele
Die Lernziele der Materialien sind nach den Taxonomiestufen des Fakultätentags1 bzw. Fachbereichstags2 Elektrotechnik formuliert. Sie reichen von der grundlegenden Wissensaneignung bis zur Anwendung komplexer Verfahren. Die didaktische Konzeption zielt darauf ab, den Lernerfolg durch interaktive Elemente und die Möglichkeit des orts- und zeitunabhängigen Lernens zu erhöhen. Langfristiges Ziel ist die Reduzierung der Abbruchquoten in den ersten Semestern, indem die Materialien den Studierenden eine flexible und tiefgehende Auseinandersetzung mit den Lerninhalten ermöglichen.
Detaillierte Materialübersicht
Die Materialien umfassen 12 Module mit allen Grundlagen der Elektrotechnik. Für alle Module stehen Materialien der folgenden Medien zur Verfügung:
- Skripte, Folien und Folienhandouts [PDF]
- Lernvideos [MP4]
- Moodle-Tests mit STACK [XML]
Für Lehrende ist der gesamte Moodle-Kurs zur eigenen Verwendung als ZIP-Download (## Link folgt ##) verfügbar.
Der Source Code des gesamten Projekts ist auf GitHub als Repository zu finden.
Die folgende Abbildung zeigt eine Übersicht, welche Software unter anderem zur Erstellung der verschiedenen Medienformate verwendet wurden.
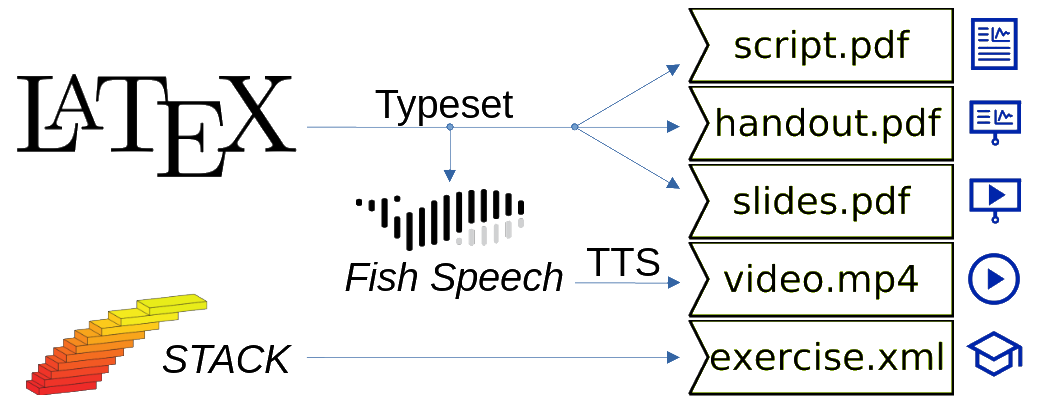
Der Sourcecode für Skripte, Folien, Handouts und Videos ist im GitHub-Repository (Link) verfügbar.
Die folgende Auflistung nennt zur Übersicht stichpunktartig die wichtigsten Themen und Inhalte wie eingeführte Konzepte, Größen und Berechnungsmethoden der einzelnen Module.
- Elektrische Grundgrößen: SI-Einheitensystem, Zehnerpotenzen (Einheiten-Präfixe), elektrische Ladung (Bohr'sches Atommodell, Coulombsches Gesetz, Flächenladungsdichte, Raumladungsdichte), das elektrische Feld (Feldstärke als Kraft pro Ladung, elektrostatische Felder), das elektrische Potential (Definition über die Arbeit, Spannung) und das elektrische Strömungsfeld (Definition der Stromdichte und Stromstärke)
- Energie und Leistung: Energieerhaltungssatz, verschiedene Energieformen, elektrische Energie(-speicher) (Kondensator, Spule, Galvanische Zelle), elektrische Arbeit, Leistung (elektrische Leistung, andere physikalische Leistungen als Potentialgröße mal Flussgröße), Wirkungsgrad (Verluste, Wärmedissipation)
- Elektrische Bauelemente: Elektrische Leitfähigkeit und elektrischer Widerstand (Driftgeschwindigkeit, Ladungsträgerdichte, Driftverhalten von Elektronen in Leitern, Spezifische Leitfähigkeit, Temperaturkoeffizienten, Kaltleiter, Widerstandsfarbcodierung), Spannungs- und Stromquellen (ideale und reale Quellen, Umrechnung von Quellen, Gleich- und Wechselstrom-/spannungsquellen), Kapazität und Kondensator (Dielektrikum, Permittivität, elektrische Flussdichte, Schaltverhalten), Induktivität und Spule (Permeabilität, Lenzsche Regel, Rechte-Hand-Regel, Schaltverhalten)
- Grundlegende Gleichstromnetzwerke: Zweipole und Zählpfeilsysteme, Grundstromkreis und Netzterminologie (Knoten, Zweige), Kirchhoffsche Sätze (Knoten- und Maschenregel), Widerstandsnetzwerke (Reihen- und Parallelschaltungen, Spannungs- und Stromteiler, Ersatzspannungsquelle/-stromquelle), Kondensatornetzwerke (Reihen- und Parallelschaltung, Spannungsteiler), Messen von Strom und Spannung (Voltmeter, Amperemeter, strom- und spannungsrichtiges Messen)
- Erweiterte Gleichstromnetzwerke: Knoten- und Maschenanalyse (Stromdichte im freien und strukturierten Raum, Exkurs Graphentheorie, benötigte Anzahl linear unabhängiger Gleichungen durch vollständigen Baum), Superpositionsprinzip (nach Helmholtz, Exkurs Systemtheorie, Kausalität, Zeitinvarianz, Linearität, Überlagerungssatz), Knotenpotentialverfahren und Maschenstromverfahren (Lineare Gleichungssysteme als Matrix mit Leitwertmatrix oder Widerstandsmatrix aufstellen und lösen)
- Magnetische Größen: Magnetismus (Magnetfelder, magnetische Feldstärke), Elektromagnetismus (Durchflutungsgesetz, rechte Hand Regel, magnetischer Fluss und magnetische Flussdichte, Permeabilität, Ferromagnetismus, Hysteresekurve), Magnetischer Widerstand (magnetischer Kreis), Lorentzkraft (Leiter und Leiterschleife mit Gleichstrom im Permanentmagnetfeld, Wirkprinzip von Elektromotoren), Induktion, Induktivität (über Feldgrößen, über magnetischen Widerstand, Luftspalt in Spulenkern), Energie im magnetischen Feld, Skin-Effekt (Skin-Tiefe), Hall-Effekt (Hall-Spannung)
- Periodische Größen: Komplexe Zahlen (Komplexe Zahlenebene, grafische Darstellung, Euler'sche Formel, kartesische Form und Polarform), Zeigerdiagramme in der Wechselstromtechnik (Periodische Wechselgrößen im Zeitbereich, komplexe Drehzeiger im Bildbereich), Komplexe Wechselstromrechnung (Impedanz, Admitanz, Verhalten von Kapazitäten und Induktivitäten, Wechselspannungs- und Wechselstromquellen und deren Umwandlung), Effektivwerte (Kurvenform, Scheitelfaktor), Scheinleistung, Wirkleistung, Blindleistung (Gleich- und Wechselanteil), Drehstromsysteme (Symmetrische und unsymmetrische Komponenten in Stern- und Dreieckschaltung), Mehrphasensysteme im Mitsystem, Gegensystem und Nullsystem (Symmetrierung für unsymmetrische Komponenten)
- Schaltungen variabler Frequenz: Wiederholung (Frequenzabhängigkeit elektrischer Bauelemente, Zweitore), Frequenzgang, Amplitudengang, Phasengang (Definition, Tiefpass und Hochpass erster Ordnung, Grenzverhalten), logarithmische Darstellung (Potenzfunktionen linear und logarithmisch dargestellt, Dezibel, Bode-Diagramme, Grenzfrequenz, Filter höherer Ordnung, Bandpass, Bandsperre), Ortskurven (Vergleich Zeigerdiagramm, Impedanz- und Admittanzortskurven), Resonanzkreise (Resonanzfrequenz, Kennwiderstand, Kennleitwert, Güte, Resonanzverhalten von idealen und realen Reihen- und Parallelschwingkreisen)
- Halbleiterbauelemente: Einführung (Bändermodell, verschiedene Halbleitermaterialien, Eigenschaften wie Gitterstruktur, Bandlücke, Eigenleitungsdichte, Elektronenbeweglichkeit, Löcherbeweglichkeit, Vorgänge wie Ladungsträgertransport, Driftstrom, Diffusionsstrom, Einfluss von Dotierung, Verhalten von pn-Übergängen), Bauelemente (Aufbau, Funktionsweise, Eigenschaften, Verhalten, Ein- und Ausgangskennlinien sowie übliche Anwendungen typischer Arten von Dioden, Bipolartransistoren und Feldeffekttransistoren mit Übersicht der speziellen Bautypen)
- Operationsverstärker: Aufbau und Funktionsweise von Operationsverstärkern, Modellierung charakteristischer Größen (Unterschiede zwischen dem vereinfachten Modell von Operationsverstärkern und realen Operationsverstärkern, die Bedeutung einzelner Größen, Vergleich idealer und typischer realer Werte, Kennlinien von Operationsverstärkern), Prinzip der Gegenkoppulung (Funktionsweise, typische Grundschaltungen mit Operationsverstärkern), Stabilität von Verstärkerschaltungen (Frequenzganganalyse, Analyse der Übertragungsfunktion, Einschwingverhalten), Operationsverstärker als Analogrechner
- Elektrische Maschinen: Klassifizierung elektrischer Maschinen, Transformator (Einsatzzwecke- und gebiete, Wirkungsprinzip, Aufbau, Ersatzschaltbild, Repräsentation von Eisen- und Hystereseverluste), Gleichstrommaschine (allgeines Funktionsprinzip, Aufbau und Gehäusekonstruktion, Feldverläufe der Magnetfelder, Berechnung von Drehmomenten und Leistungen, Ersatzschaltbilder, fremderregte Gleichstrommaschine und Reihenschlussmaschine), Synchronmaschine (Eigenschaften, Aufbau, Feldverläufe, Ersatzschaltbild) und Asynchronmaschine (Aufbau einer Käfigläufer-Asynchronmaschine, Wirkungsmechanismen beim Anlaufen und im Betrieb, Klosssche Kennlinie und Schluf einer Asynchronmaschine) mit Gegenüberstellung der Vor- und Nachteile der drei genannten Arten elektrischer Motoren beziehungsweise Generatoren
- Schaltvorgänge: Einführung (allgemeine Ausgleichsvorgänge, Ablauf, Ursachen und Beispiele von Schaltvorgängen, Vergleich idealer und realer Schalter), Grundlagen (Definitionen, prinzipielle Berechnungsmethoden im Zeit- und Bildbereich zum Aufstellen und Lösen von Differentialgleichungen, Berechnungsverfahren im Zeitbereich durch Zerlegung in flüchtigen und eingeschwungenen Zustand), Schaltvorgänge (Berechnung bei Gleichspannung und bei Wechselspannung für RC- und RL-Schaltungen sowie RLC-Schwingkreisen, Einschwingverhalten bei einem aperiodischen Fall, einem Grenzfall und einem Schwingungsfall, Größen wie Zeitkonstante, Diskriminante, Abklingkonstante und gedämpfte Eigenkreisfrequenz, Exkurse für Schwingkreise zur Überlagerung von Schwingungen, zum Vergleich von Polstellen der Übertragungsfunktion und den Zusammenhang von Güte Eigenfrequenz und Dämpfungskonstante)
Eine gute Übersicht zu allen Themen und Gelegenheit zum Stöbern und Einlesen bietet außerdem das Gesamtskript (PDF-Link). Es umfasst die Skripte aller 12 Module und lässt sich gut über das Inhaltsverzeichni, die PDF Bookmarks, Suchfunktionen oder das Index-Register am Ende navigieren.
Auch bietet sich die HTML-Version der einzelnen Skripte auf dieser Website unter dem Punkt Module oder die HTML-Version für das Index-Register an, um über einschlägige Begriffe Kapitelstellen mit deren Erwähnung zu finden.
Planung einer Vorlesung mit den Materialien
Inhalte und Taxonomiestufen
Die effektive Planung einer Vorlesung beginnt mit der Auswahl der relevanten Inhalte. Für Studierende der Elektrotechnik werden diese beispielsweise vom Fakultätentag Elektrotechnik und Informationstechnik (Universitäten)3 oder vom Fachbereichstag Elektrotechnik (HAWs)2 festgelegt und jeweils mit den empfohlenen Taxonomiestufen verknüpft. Diese Empfehlungen bilden einen inhaltlichen und didaktischen Rahmen, der sicherstellt, dass die vermittelten Kompetenzen bundesweit anerkannten Standards entsprechen.
Im Grundstudium dominieren die Taxonomiestufen 1 (Wissen), 2 (Verstehen) und 3 (Anwenden). Höhere Stufen wie 4 (Analysieren), 5 (Entwerfen) und 6 (Bewerten) kommen hier lediglich in ausgewählten Themengebieten oder in vertiefenden Übungen zum Einsatz. Für Studierende anderer Fachrichtungen existieren vergleichbare Empfehlungen, z. B. vom Fakultätentag Maschinenbau oder dem Fakultätentag Informatik.
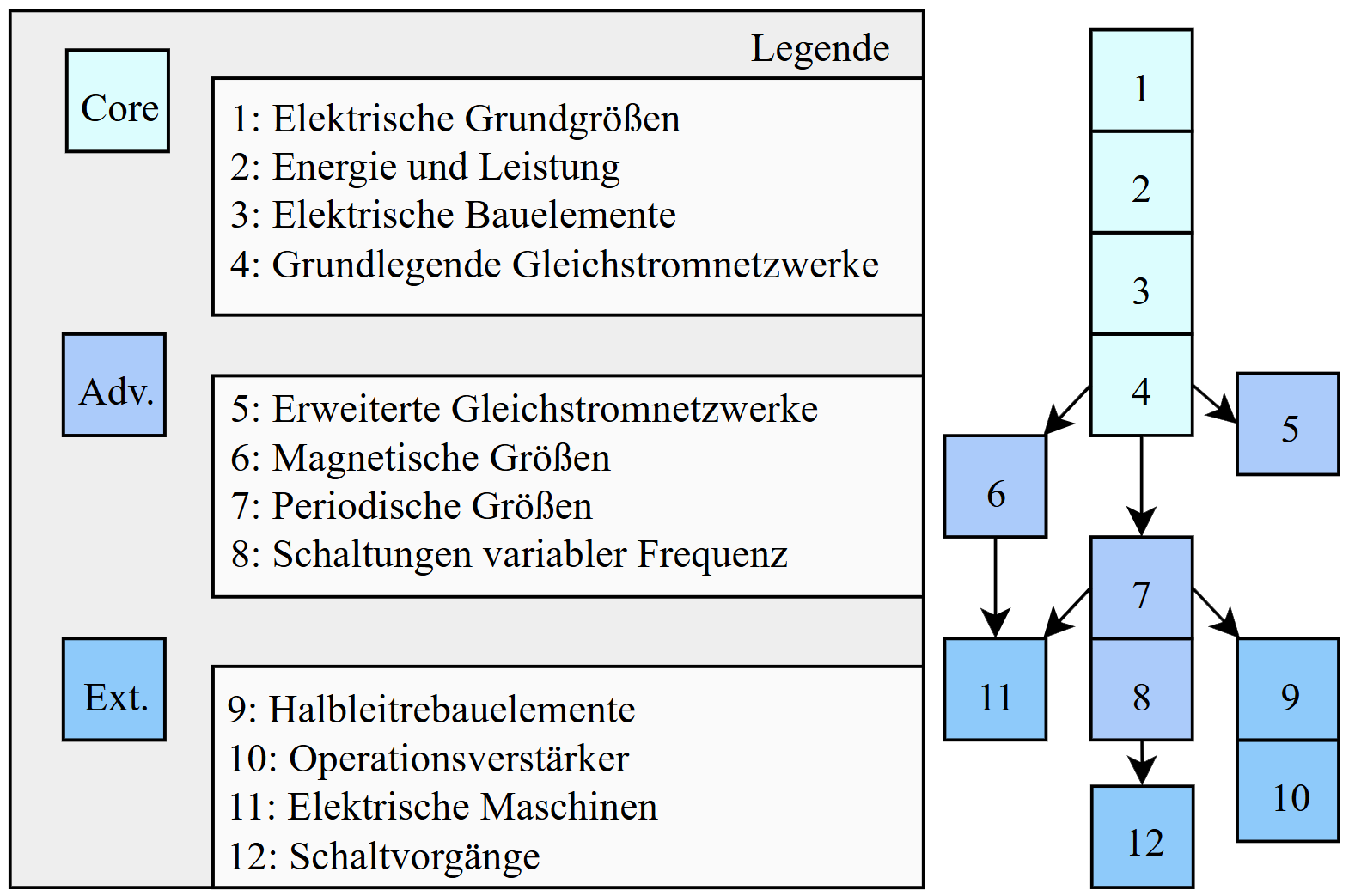
Bei der Nutzung dieser in einer Art Baukastensystems enthaltenen Materialien sind teilweise aufeinander aufbauen, so dass zum Verständnis der nachfolgenden Themen bereits von den Studierenden behandelt sein sollten. Eine Übersicht über die Abhängigkeiten der in Grundlagenwissen (Core), fortgeschrittenes Wissen (Advanced) sowie erweitertes Wissen (Extended) ist in der folgenden Grafik dargestellt.
Lernziele
Die sorgfältige Definition von Lernzielen ist entscheidend für eine zielgerichtete und effiziente Lehrveranstaltung. Sie dient als verbindendes Element zwischen den Inhalten und der gewählten Taxonomiestufe, und sollten die nach dem Durcharbeiten der Materialien erlangten Fähigkeiten der Studierenden als Aussagen beschreiben. Beispielhafte Lernziele sind zu Beginn und Ende eines jeden Moduls in den Foliensätzen sowie im Skript aufgeführt.
Eine konsequente Ausrichtung der Lernziele an den Taxonomiestufen und die bewusste Kombination verschiedener Medien steigern die Wirksamkeit der Lehre und erleichtern den Studierenden den Übergang von der reinen Wissensaufnahme hin zu einer sicheren Anwendung und Analyse des Erlernten.
Beispielhafte Integrationen (Universitäten & HAWs)
Nachfolgend sind einige Beispiele aufgeführt, welche der erstellten Materialien in beispielhafte real durchgeführte Lehrveranstaltungen an Universitäten bzw. HAWs durchgeführt wurden.
-
Maschinenbau, Universität
In der Lehrveranstaltung "Grundlagen Elektrotechnik für Maschinenbau", welche im 3. Fachsemester gelesen wird, wird folgende Struktur unter Verwendung der angegebenen Module genutzt:
- Einführung: Teile von Modul 1
- Elektrostatisches Feld: Teile von Modul 1, Kraft- und Energiebetrachtungen aus Modul 2 sowie der Kondensator aus Modul 3
- Stationäre elektrische Ströme: Teile von Modul 1 sowie den elektrischen Widerstand aus Modul 3
- Gleichstromnetzwerke: Modul 4 (komplett) sowie Teile aus Modul 5
- Statisches Magnetfeld: Stationärer Teil aus Modul 6
- Zeitlich veränderliche Magnetfelder: Zeitabhängige Teile aus Modul 6
- Zeitlich veränderliche Spannung und Ströme: Modul 7 sowie Grundlagen der Ausgleichsvorgänge aus Modul 12
- Gleichstrommaschine: Nur Grundlagen zur Gleichstrommaschine aus Modul 11
-
Informatik, Universität
-
Elektrotechnik, HAW
-
Fahrzeugtechnik, HAW
Adaption der Materialien auf eigene Vorlesungen
Nachfolgend Schritte zur Integration in eigene Lehrveranstaltungen.
Einrichten der Entwicklungsumgebung unter Ubuntu 24.04
Um die Get it Digital LaTeX Dokumente lokal kompilieren zu können, wird die Bearbeitung mit Visual Studio Code (VSCode) mit der Erweiterung LaTeX Workshop in einer Docker Umgebung empfohlen.
Dependencies installieren
Zum Einrichten der empfohlenen Entwicklungsumgebung sollten die folgenden Programme (Git, Visual Studio Code und Docker) installiert werden.
Führen Sie im Terminal folgend Kommandos aus:
sudo apt install -y git
snap install code
code --install-extension james-yu.latex-workshop
code --install-extension ms-azuretools.vscode-containers
code --install-extension ms-azuretools.vscode-docker
Installieren Sie Docker wie in der offiziellen Dokumentation beschrieben:
https://docs.docker.com/engine/install/ubuntu/
Um Docker als non-root user zu verwenden, können die Anweisungen hier befolgt werden:
(Risikohinweis beachten.)
https://docs.docker.com/engine/install/linux-postinstall/#manage-docker-as-a-non-root-user
Laden Sie nun das Repository mit den LaTeX Source Dateien herunter und starten VSCode im GetItDigital Ordner mit den folgenden Kommandos:
git clone https://github.com/GetItDigital/GetItDigital
cd GetItDigital
code .
Unten rechts im Eingabefenster sollte beim Start eine Eingabeaufforderung erscheinen. Bestätigen Sie, dass der Ordner im .devcontainer Container geöffnet werden soll. VSCode erstellt hierfür beim ersten Aufruf automatisch das nötige Docker Image. Dies kann beim ersten mal einige Minuten dauern.
Einstellungen in VSCode
Für LaTeX Workshop müssen noch zwei Einstellungen vorgenommen werden.
1. Output Directory einstellen
Im Output Ordner werden die kompilierte PDFs und alle auxillary files gespeichert. Dieser sollte auf jedenfall eingestellt werden, damit die Ausgangsdateien nicht gleichen Ordner wie die Quelldateien landen!
Hierfür in VSCode links im Reiter Extensions die Erweiterung LaTeX Workshop auswählen.
Die Einstellungen zu LaTeX Workshop öffnen und nach "Output" Directory suchen.
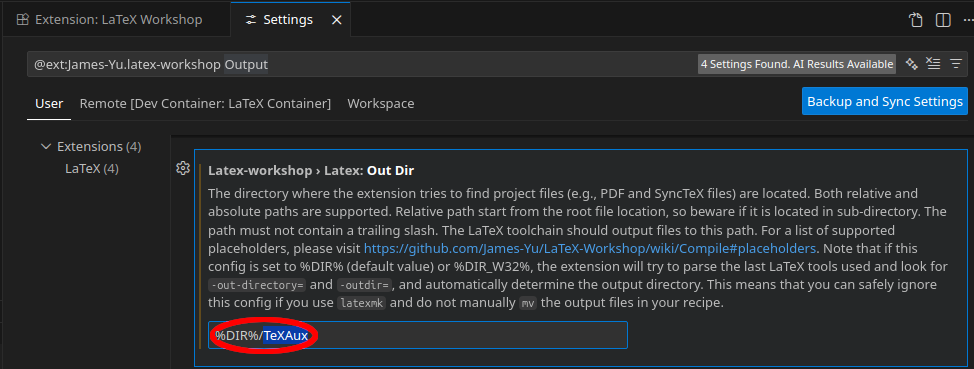
Der Ordner muss auf ./TeXAux gesetzt werden.
2. latexmk -shell-escape einstellen
Die zweite Einstellungsänderung betrifft die Berechtigung für latexmk beim Kompilieren Befehle in einer Shell ausführen zu können.
Diese werden genutzt, um die in Inkscape erstellten Graphiken richtig zu rendern (LaTeX Math Texte),
TiKz Bilder einmalig zu prekompilieren (um sie später als PNGs nutzen zu können),
Gnuplots und Indizes korrekt zu erstellen. (Vgl. \write18{...} Befehle in .texDateien.)
Hierfür in den LaTeX Workshop Einstellungen nach recipe suchen und die settings.json bearbeiten.
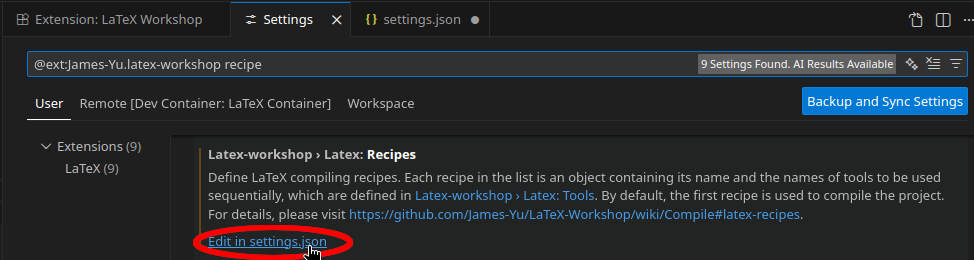
Beim recipe wird das standardmäßig das oberste recipe zum Kompilieren von
Dateien verwendet.
Hier erstellen wir ein neues default receipe namens latexmk (shell-escape), welches das Tool latexmk-shell-escape aufruft.
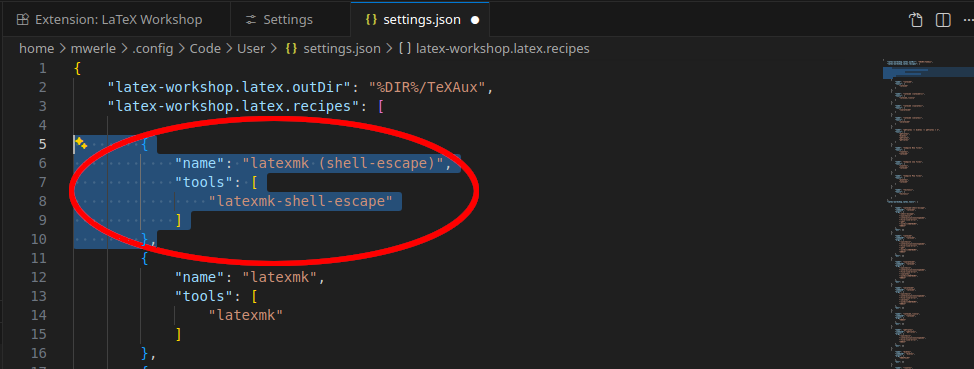
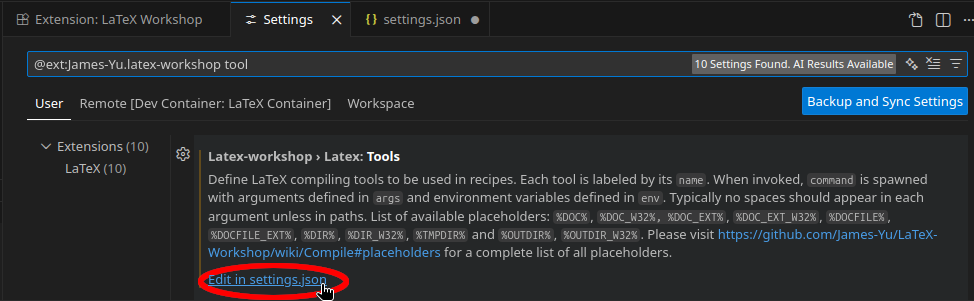
Um das neue Tool zu definieren, zunächst wieder in den Optionen der Erweiterung nach "Tool" suchen und die Bearbeitung in der settings.json anklicken.
Erst danach tauchen in der settings.json die Einträge für die Tools auf.
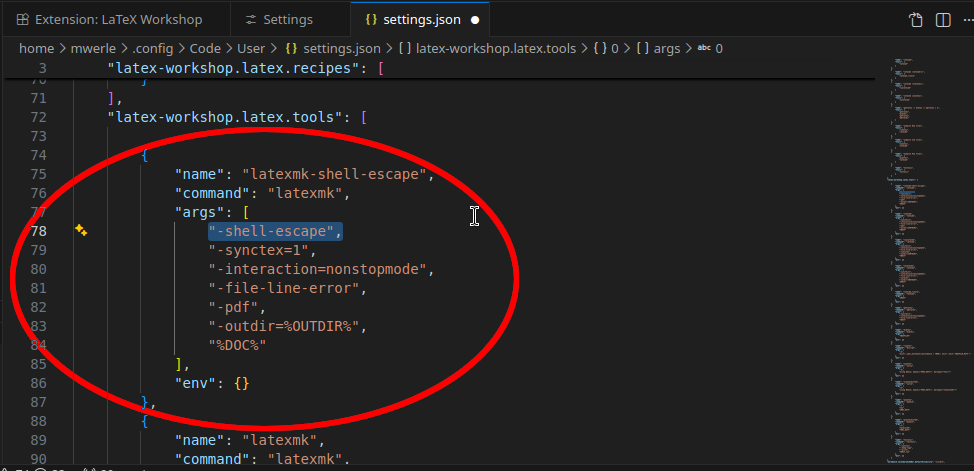
Nun können wir unseren Tool-Eintrag hinzufügen. (Das latexmk Tool kopieren und den Tag -shell-escape hinzufügen.)
Nun können Sie in den einzelnen Modulen die Skript.tex oder die Folien.tex kompilieren,
und ebenso das Gesamtskript Skript.tex über alle 12 Module.
Problembehandlung
Wenn die Kompilierung eines LaTeX Dokuments nicht funktioniert, kann es helfen, den Ordner TeXAux komplett zu löschen und "from scratch" zu Kompilieren.
Bei Problemen die Dateien im Hostsystem (außerhalb vom Container in VSCode) zu nutzen, können Berechtigungen eine Rolle spielen.
Im Docker Container werden alle Dateien als root user erstellt, was manchmal dazu führt, dass die Berechtigungen für non-root-user im Host System nicht ausreichen.
Eine Möglichkeit ist die die ownership von root zum user zu ändern für die betroffenen Dateien.
Hierfür im Hostsystem im Terminal in den Ordner wechseln (cd ) und dann mit chown die ownerhsip von einer Datei oder von allen Dateien im Ordner (./*) ändern.
Vorher und nacher die Ownership mit ll prüfen (Kurzform für ls -l).
cd TeXAux
ll
sudo chown $USER:$USER ./*
ll
##Einrichten der Entwicklungsumgebung unter Windows
Bearbeiten der Lehrvideos
Im Folgenden wird ein Workflow beschrieben, mit dem sich automatisiert aus dem Inhalt von 'speech'-Makros mithilfe lokaler KI-gestützter Spachsynthese mit 'fish-speech' (aka. OpenAudio) Audiodateien erzeugen lassen. Als Quelle wird ein Text und ein Audiosample als Stimmreferenz benötigt. Der Text wird jeweils durch die Verwendung von 'speech'-Makros im LaTeX-Quelltext des Skriptes bzw. der Folien bereitgestellt. Die Stimmreferenz ist im Projekt-Template hinterlegt, könnte aber auch durch eine eigene Referenz ersetzt werden. Ausgegeben wird eine Audiodatei im WAV-Format, die im weiteren Schritt zusammen mit einem Beamer-Frame (Folien-PDF) zur Erstellung einer Videodatei weiterverarbeitet wird.
Voraussetzungen
- Der Computer verfügt über eine dedizierte Grafikkarte (GPU). Eine prozessorinterne Grafikeinheit reicht leider nicht. Ohne Grafikkarte geht es zwar prinzipell auch, die Spracherzeugung dauert dann aber Stunden statt Minuten.
- Die folgenden Projektdateien werden dazu benötigt:
- MakeTTS.py (API-Schnittstelle zu fish-speech)
- TTSCrate.sh (Skript zum Erstellen der einzelnen Audiodateien)
- VideoCreate.sh (Skript zum Erstellen der einzelnen Videodatein)
- VideoTitle.tex (Erstellt Titelbilder für die einzelnen Videos)
- Sprachsample.wav (Audiosample als Referenz für fish-speech)
- beamervideo.sty (Latex-Paket, das beim Kompilieren die Bash-Dateien zum Rendern der Einzelvideos erzeugt)
- Verzeichnis "Videovorlagen" (das Verzeichnis enthält Intro und Outro)
- Es wird das aktuelle Docker-Image 'latest-video' des Projekts verwendet (definiert in '.devcontainer/devcontainer.json'). Ist das aktuelle Template gemerget, ist dies bereits konfiguriert.
Modul-Container in benutzerdefiniertem Netzwerk starten
Damit die beiden Docker-Container über eine fest definierte IP kommunizieren können, muss ein benutzerdefiniertes Netzwerk innerhalb der Docker-Umgebung erstellt werden.
Wenn die aktuelle Version des Templates gemerget wurde, ist im Projektordner/.devcontainer die Datei 'docker-compose.yml' dazu vorhanden und die Container-Konfigurationsdatei '.devcontainer/devcontainer.json' bereits entsprechend angepasst:
"name": "TeX Container",
"service": "tex",
"dockerComposeFile": "../docker-compose.yml",
"workspaceFolder": "/workspace",
"shutdownAction": "stopCompose",
"extensions": ["james-yu.latex-workshop"]
'fish-speech' einrichten
- Doppelklick auf die Datei 'StartFish.bat' (im Verzeichnis 'Video').
- Das Fenster mit der Eingabeaufforderung muss geöffnet bleiben. Der Container läuft solange, bis das Fenster geschlossen wird.
- Installation prüfen, indem im Webbrowser das GUI gestartet wird: http://localhost:7860
Der Container braucht insbesondere beim ersten Starten ein paar Sekunden bis er läuft. Es sollte die Weboberfläche von fish erscheinen. Der Text "Das ist ein Test" sollte ca. 3-4 Sekunden dauern. Wenn es erheblich länger braucht, kann evtl. keine Grafikkarte gefunden werden.
Verwenden des Workflows
Text-To-Speech Sprachsynthese
Voraussetzung: Der Docker-Container von fish-speech läuft bereits.
Alle 'speech'-Makros, die zu einem Beamer-Frame gehören, stehen immer am Ende des Frames, bevor es mit \end{frame} geschlossen wird.
Ein 'speech'-Makro benötigt immer drei Argumente: \speech{Dateiname}{Frame-Nummer}{Inhalt}
- Audiodateien aus vorhandenen 'speech'-Makros erzeugen durch Aufruf des Bash-Skripts in der Kommandozeile
von
VS Code:
./TTSCreate.sh - Die Audiodateinen werden nach dem ersten Argument (Dateiname) des 'speech'-Makros benannt und im Verzeichnis 'TTS' abgelegt.
- Es werden nur Audiodateien erzeugt, wenn diese noch nicht existieren oder wenn Änderungen im 'speech'-Makro vorgenommen wurden. Im zweiten Fall werden die Audiodateien überschrieben.
- Es ist sinnvoll, die ausgegebenen Audiodateien auf korrekte Betonung probezuhören.
- Der Workflow nutzt einen zufälligen Seed, sodass Audiodateien bei denen z. B. die Betonung nicht gefällt mit neuem Seed erneut erstellt werden können. Dazu kann die zugehörige Datei mit der Endung '.seed' aus dem TTS-Verzeichnis gelöscht werden. Der letztlich verwendete Seed wird beim Commit hinterlegt, sodass die Ergebnisse wiederherstellbar sind.
Videoerzeugung
Voraussetzung: Die zugehörigen Audiodateien sind bereits erzeugt und im Ordner 'TTS' abgelegt.
Um Videos in passende Länge (max. 10 Min) zu zerteilen, werden mithilfe des 'newvideofile'-Makros die Abschnitte im Dokument festgelegt. Bei jedem Auftreten des Makros wird ein neues Video erzeugt.
Ein 'newvideofile'-Makro benötigt immer zwei Argumente: \newvideofile{Dateiname}{Titel}
- Videodateien erzeugen durch Aufruf des Bash-Skripts in der Kommandozeile von VS Code:
./VideoCreate.sh - Titelbilder mit entsprechenden Titeln zu den Videos werden aus dem zweiten Argument (Titel) des 'newvideofile'-Makros generiert.
- Die Teildateien (je Audiodatei und Beamer-Frame) werden im Verzeichnis 'TeXAux/video' ausgegeben.
- Die zusammengefügten 'finalen' Videodateien – ergänzt mit Intro, Videotitel und Outro – werden nach Modulnummer, Videonummer innerhalb des Moduls sowie dem ersten Argument (Dateiname) des 'newvideofile'-Makros benannt und im Verzeichnis 'Videos' abgelegt. Vorhandene Dateien werden dabei überschrieben und durch die aktuelle Version ersetzt.
Nutzen und bearbeiten der STACK-Aufgabensammlung
Dies ist ein Quick Guide als kurze Einführung in die Erstellung von STACK Aufgaben für Moodle.
STACK Übersicht
STACK ist ein open-source online Prüfungssystem für MINT-Fächer und als Moodle Plugin verfügbar.
Mit dem Plugin ist es möglich Fragen vom Typ STACK anzulegen.
Diese sind ähnlich wie der Typ Berechnet nutzbar, allerdings mit deutlich mehr Möglichkeiten.
STACK features umfassen u.a.:
- Strukturiertes Randomisieren von Fragen.
- Verschiedenste Antworttests für unterschiedliche Arten von Input.
- Interaktive Graphen mit JSXGraph einbinden.
- Individuelles Feedback je (Teil-)Aufgabe.
- Berücksichtigung von Folgefehlern.
Frage erstellen
Anhand der STACK Frage How-to-STACK Beispielaufgabe wird Schritt für Schritt erklärt, wie eine einfache STACK Aufgabe erstellt werden kann.
Die STACK Frage finden Sie im Moodle Kurs dieser Anleitung. Die Namen der Abschnitte im Guide orientieren sich an den *kursiv* geschriebenen deutschen Bezeichnungen der Eingabebereiche in Moodle beim Bearbeiten einer STACK Aufgabe.
Aufgabenvariablen (Question variables): Maxima Grundlagen
Variablen werden hier mit variable: value; Werten zugewiesen, z. B. R: 12;.
Zudem können Berechnungen und Randomisierung von Variablen durchgeführt werden.
Die Syntax entspricht der von Maxima, da STACK im Hintergrund Maxima als Computer-Algebra-System nutzt zuzüglich einiger stack-spezifischer Funktionen. Befehle enden mit Semikolon.

Hilfreiche Kommandos:
decimalplaces(val, n);zum Runden vonvalauf dien-te Nachkommastelle.float(num);zum Ausgeben vonnumals Fließkommazahl (statt als Berechnungsterm, fallsnumberechnet wird).rand(list);zum Randomisieren mitlist: [a1, a2, ..., aN];z. B.rand([1,4,9,16,25]);rand_with_steps(start, end, stepsize);
Tipps:
- Musterlösungen (Teacher answers) am Besten mit
tans1,tans2,tans3u.s.w. benennen. - Es hilft Variablen einheitenlos zu definieren z. B.
R: 12;,Iq: 0.5; - und Musterlösungen mit Einheit z. B.
tans1: decimalplaces(R*Iq, 2) * V;. - STACK kennt die meisten physikalischen Einheiten und kann diese automatisch umrechnen, die Berechnung in Maxima ist ohne Einheit aber einfacher.
Referenz: STACK Docs: Maxima and computer algebra use in STACK
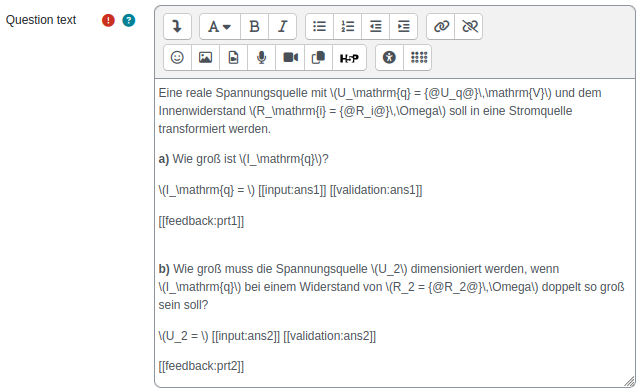
Fragetext (Question text): Formatierung, LaTeX, HTML, Editor
LaTeX-Math mit \( und \) für Inlinemath und mit \[ und \] für Displaymath.
Mit {@var@} lässt sich der Wert der Variable var aus den Aufgabenvariablen anzeigen. Das geht auch im LaTeX Math Modus,
z. B. \( R = {@R_ohm@}\,\Omega \).
Felder für Input, Validierung und Feedback werden am besten zusammen an der entsprechenden Stelle im Fragetext eingebunden.
\( U_2 = \) [[input:ans1]][[validation:ans1]]
[[feedback:prt1]]
Opional: In der Sourcecode Ansicht lassen sich im HTML Code auch Javascripte einbinden, z. B. um die Eingabe in Antwortfeldern zusätzlich zu limitieren. (z. B. maximale Anzahl an Ziffern vor oder nach dem Dezimal) S. Abschnitt zu JavaScript.
Optional: JSXGraph wird im Question Text eingebunden. Mehr dazu im Abschnitt zu JSXGraph.
Aufgabenhinweis (Question hint): Unterscheidung von Varianten
Wird benötigt, um unterschiedliche Varianten voneinander zuterscheiden zu können, wenn Variablen randomisiert werden.
Varianten werden nur anhand unterschiedlicher Strings in diesem Eingabefeld unterschieden.
Randomisierte Variablen müssen deshalb mit {@var@} eingebunden werden.
Hilfreich ist es auch Musterlösungen einzubinden, um später z. B. Fragevarianten mit zu einfachen Lösungen zu löschen.
z. B. vars: {@U_q@}; {@R_i@}; {@R_2@}; tans: {@tans1@}; {@tans2@}; {@tans3@}; {@tans4@}

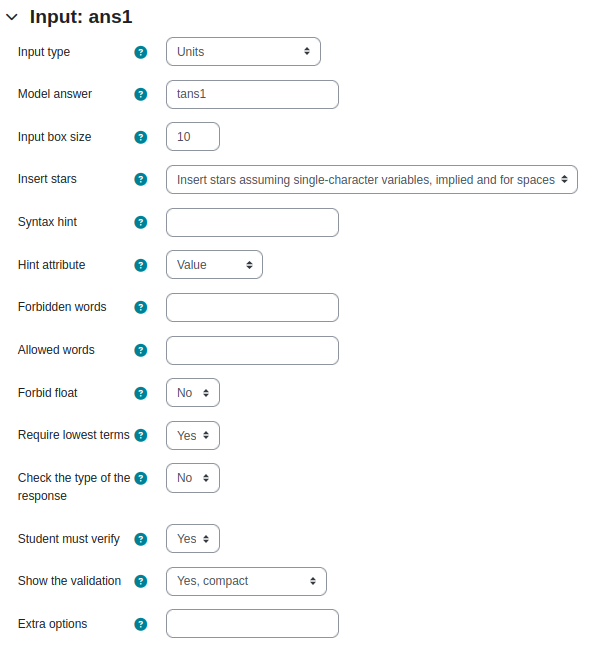
Eingabe (Input): Input-Felder, Antworttypen und Musterantworten
Hier werden u.a. die Input Formate für die Eingabefelder und die anzeigbaren Musterlösungen definiert/angegeben.
Wenn die Einstellungen nicht für alle Eingabefelder aus dem Question Text angezeigt werden, den Button Verify the question text and update the form betätigen.
Die Input Typen sollten zu den später im Rückmeldebaum angegebenen Antworttests passen.
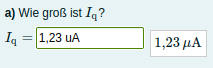
Die Option Show the validation mit Yes, compact kann hilfreich sein, speziell für Einheiten Tests,
damit Studis direkt erkennen, ob die Eingabe auch als die korrekte Einheit erkannt wird.
Das sieht im Test dann (live während der Eingabe!) wie folgt aus:
Rückmeldebäume (Response trees): Antworttests, Folgefehler Berücksichtigung
Je Frage bietet sich ein eigener Rückmeldebaum (prt) an.
Im Feld Feedback variables kann (optional) mit Eingaben aus den Fragen wie im Feld Question variables gerechnet werden.
Dadurch ist es möglich alternative Lösungen zum Beispiel zur Berücksichtigung von Folgefehlern zu berechnen.

Falls Rückmeldebäume fehlen, im Question Text (s.o.) die Blöcke [[feedback:prt2]], etc. hinzufügen und Verify question text and update form betätigen.
Im einfachsten Fall: Ein Node mit zu vergleichendem Input (SAns) z. B. ans1, der zu vergleichenden Musterlösung (TAns) z. B. tans1 und der Antworttest z. B. UnitsAbsolute auswählen, gegebenenfalls mit (antworttest-spezifischer) Test Option z. B. 0.01 für eine (absolute) Genauigkeit auf die zweite Nachkommastelle. Der Score im Node ist relativ zwischen 0 bis 1 anzugeben (für 0 bis 100 %).
Beim Node Feedback können neben Question variables auch Feedback variables und Eingaben verwendet werden, z. B. mit {@roundU_2FF@} oder {@ans1@}.
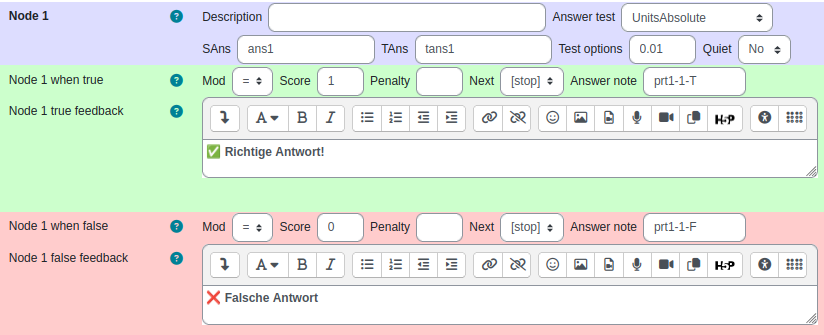
Durch hinzufügen und verknüpfen von Nodes lassen sich Folgefehler oder fast-richtige Antworten berücksichtigen.
Mehr Infos zu Antwort Tests, Ref:
- STACK Docs: Answer tests (Link)
- STACK Docs: Answer test results (Link)
- STACK Repo: Answer test results (Tabellen schöner) (Link)
Fortgeschrittenes
Randomisierung und Varianten
Beim Randomisieren von Question variables mit Befehlen wie rand(N) oder rand_with_steps(min,max,steps)
JSXGraph: Einbinden interaktiver Graphen
Achtung: Der Text-Editor kann beim Einbinden von JSXGraph Code Probleme machen. Zum Ändern des Editors in den persönlichen User Einstellungen global den Editor wechseln. Zum einbinden von JSXGraph empfiehlt sich eher der Atto-Editor oder der Plain Text Editor.
| Texteditor | Vorteile Text | Nachteile Text | Vorteile Code | Nachteile Code |
|---|---|---|---|---|
| TinyMC (Default) | Textbearbeitung mit GUI, Bilder einbinden | HTML-Code schlecht formatiert –> LaTeX Code anfällig für Fehler
z.B: \(U_1 = <span> 5\,\mathrm{V} \) </span>
(<span></span> und \( \)
überlappen.) |
Zeilenumbrüche und Einrückungen werden geschluckt, Sonderzeichen wie “<”, “>”, “&” werden umformatiert | |
| Atto Editor | vergleichbar mit Tiny MC | vergleichbar mit TinyMC | Einrückungen werden geschluckt, Sonderzeichen wie “<”, “>”, “&” werden umformatiert | |
| Plain Text | HTML-Code lässt sich gut formatieren | Keine GUI, Textformatierung in HTML Syntax nötig
(<b>fett</b>,
<i>kursiv</i>, <br> für
Zeilenumbruch, …)
|
Formatierung bleibt erhalten |
- TinyMC Für sehr einfache JSXGraphen auch geeignet. Der Code wird dann als Einzeiler(!) im Sourcecode gespeichert. (Code ohne Sonderzeichen, Kommandos immer mit ";" abschließen, Kommentare nur mit
/* Kommentar */, nie mit// Kommentar.) - Atto Für die meisten JSXGraphen geeignet. Zeilenumbrüche bleiben erhalten. Auf
&,>,<muss im Code verzichtet werden. Dadurch ist die Bearbeitung des Textes und des Codes möglich und der Code bleibt einigermaßen leserlich. - Plain Text Kompliziertere JSXGraphen, die Sonderzeichen verwenden (z. B. für if-else-Abfragen, Schleifen, ...) sollten immer im Plain Text Editor gespeichert werden.
JavaScript: Einbinden von Skripten zur Limitierung der Eingabe
Mit der Einbindung eines JavaScript in den Quellcode des Fragetextes kann das Format der Eingaben beschränkt werden, damit z. B. max. zwei Dezimalstellen, ausschließlich Komma als Dezimalzeichen oder max. vier Stellen vor dem Komma eingegeben werden können.
Ein Beispiel-Skript ist hier zu finden: InputLimiter.js
Dieses Beispiel benötigt jQuery für den Zugriff auf die Elemente im DOM. Das Skript inkl. jQuery kann mit dem folgenden Code am Ende des Fragetext-Quellcodes eingebunden werden:
<script src="https://code.jquery.com/jquery-3.7.1.min.js" integrity="sha256-/JqT3SQfawRcv/BIHPThkBvs0OEvtFFmqPF/lYI/Cxo=" crossorigin="anonymous"></script>
<script src="pfad/InputLimiter.js"></script>
Dieses Skript enthält außerdem ein Workaround für einen aktuell noch vorhandenen Bug von JSXGraph, der in Verbindung mit Kommata als Dezimalzeichen besteht!
Weiterführende Links
- https://stack-assessment.org/STACK Website: (Link)
- https://moodle.org/plugins/qtype_stackMoodle Plugin STACK: (Link)
Integration didaktischer Methoden
Nutzen Sie die Materialien, um verschiedene didaktische Methoden effektiv umzusetzen. Beispielsweise können Studierende vor der Präsenzphase die Videos und Skripte eigenständig bearbeiten und während der Präsenzveranstaltung spezifische STACK-Aufgaben in Gruppen lösen.
Think-Pair-Share
Bei dieser Methode werden den Studierenden Verständnisfragen im Multiple-Choice-Format zum vorher vermittelten Stoff gestellt. Häufig werden dabei Fehlvorstellungen aufgegriffen, welche typischerweise bei Studierenden herrschen. Anschließend werden die Studierenden aufgefordert, ihre Antwort mithilfe eines Audience Responses Systems wie beispielsweise PINGO3 einzugeben.
Anschließend sollen die Studierenden versuchen, ihre Nachbarn von ihrer Antwort zu überzeugen bzw. sie ihnen plausibel zu erklären. Dadurch lernen die Studierenden die Denkweisen ihrer Kommilitonen kennen und üben dabei, ihre eigenen Gedanken zu den Problemstellungen klar zu strukturieren. Eine zweite Antwortrunde auf dieselbe Frage gibt Einblicke, ob der Prozess erfolgreich war.
Falls sich bereits in der ersten Fragerunde abzeichnet, dass nur die wenigstens Studierenden die Antwort auf die Frage kennen (z. B. < 30%), oder die Antwort bereits fast allen bekannt ist (z. B. > 80%), kann gegebenenfals auf eine zweite Runde verzichtet werden, und der bzw. die Dozierende sollte sich dem Thema selbst noch einmal ausführlich widmen, oder im zweiten Fall die Lösung mit einer kurzen Erklärung direkt liefern.
Problem-Based Learning (PBL)
Während in den Vorlesungen in der Regel nicht genug Zeit ist, bietet sich das Problem-Based Learning (PBL) beispielsweise im Tutorienbetrieb an. Dazu bekommen die Studierenden eine praxisnahe Problemstellung wie beispielsweise das Design und die Dimensionierung eines kleinen Messaufbaus, welche sie weitestgehdend eigenständig mit den zur Verfügung gestellten Aufgaben lösen sollen. Die Tutoren treten dabei nicht als klassische Lehrperson auf, sondern moderieren den Lernprozess in erster Linie. Diese Lehrform wird meist in Gruppenarbeit durchgeführt, wodurch in jedem Teilschritt Absprache der Gruppenmitglieder untereinander erzwungen wird, was jedem einzelnen Teilnehmer die Chance zu einer Selbstreflexion bietet. Diese Methode fördert die Problemlösekompetenzen der Studierenden sowie den Transfer theoretisch erlangten Wissens auf praktische Problemstellung.
Blended Learning
Je nach Struktur der jeweiligen Einrichtung können die Inhalte sinnvoll im Blended-Learning-Format unterrichtet werden, da sämtliche Materialien sowohl für die Verwendung in Vorlesung als auch für das Selbststudium vollständig aufbereitet sind. Studierende erarbeiten sich zunächst mithilfe von Skripten und Vorlesungsvideos die grundlegenden Konzepte in ihrem eigenen Lerntempo. Interaktive STACK-Aufgaben ermöglichen eine direkte Rückmeldung und festigen das Verständnis vor der Präsenzveranstaltung. In der gemeinsamen Vorlesungs- oder Übungszeit steht dann nicht mehr die reine Wissensvermittlung im Vordergrund, sondern die Anwendung auf komplexere Problemstellungen, die Diskussion typischer Fehler und die Klärung offener Fragen. Durch diese Struktur wird die Präsenzzeit deutlich interaktiver, und heterogene Vorkenntnisse lassen sich leichter ausgleichen. So entsteht ein flexibler und nachhaltiger Lernprozess, der sowohl Motivation als auch Lernerfolg steigert.
Schlussbemerkung
Hier, auf der offiziellen Projektwebseite, finden sie alle Materialien, technische Dokumentationen und Anleitungen zur optimalen Nutzung der Werkzeuge wie STACK und zur Videoerstellung. Nutzen sie diese Ressourcen aktiv zur Unterstützung Ihrer Lehrtätigkeit und zögern sie nicht, sich mit Fragen und Anmerkungen an die dort aufgeführten Kontaktadressen zu wenden.
Beteiligte Hochschulen