Asynchronmaschine

Die Asynchronmaschine ist ebenfalls eine Drehfeldmaschine. Der Stator ist identisch zum Stator der Synchronmaschine, der Rotor ist hingegen in der häufigsten Version dieses Maschinentyps, beim sogenannten Käfigläufer, passiv.

1 Aufbau

PIC

Abbildung 1: Aufbau einer Käfigläufer-Asynchronmaschine. Die Bleche des Rotorzylinders wurden der Anschaulichkeit halber zur Hälfte beschnitten, um den Käfig freizulegen.

2 Käfigläufer

  • In den Nuten des Läuferblechpaketes liegen leitfähige Stäbe.
  • Stirnseitig sind die Stäbe durch Kurzschlussringe miteinander verbunden.
  • Zusammen bilden diese Komponenten einen Käfig (ähnlich Hamsterkäfig).
  • Stäbe werden geschrägt ausgeführt zur Reduktion von Oberwellen im umlaufenden magnetischen Feld.
PIC
Abbildung 2: Käfig eines Asynchronrotors. Zur Hälfte mit Blechpaket gezeigt.

3 Anlauf der ASM

  • Der Stator erzeugt im Ständer eine umlaufende magnetische Wanderwelle mit der Winkelgeschwindigkeit: \(\omega _\mathrm {s} = \frac {\omega _0}{p}\).
  • Der ruhende Läufer sieht ein veränderliches Feld mit der Frequenz \(\omega _\mathrm {s}\).
  • Das magnetische Drehfeld durchsetzt den Läufer und induziert eine Spannung mit der Frequenz \(\omega _\mathrm {s}\).
  • Aus der Spannungsinduktion resultiert ein Stromfluss, da die Läuferwicklungen kurzgeschlossen sind.
  • Der induzierte Rotorstrom wirkt der von ihm gesehenen Änderung des Statorfeldes entgegen (Lenzsche Regel).
  • Statorfeld und Rotorstrom wechselwirken durch die Lorentzkraft- es kommt zur Ausbildung eins Drehmoments.
  • Das Drehmoment wirkt in Richtung des Ständerdrehfelds.
  • Der Läufer beginnt sich zu drehen.

4 Betrieb der ASM

  • Mit steigender Drehzahl des Läufers sieht dieser eine immer langsamere Änderung des Statorfeldes: \(\omega _\mathrm {r} = \omega _\mathrm {s} - \omega _\mathrm {mech}\).
  • Mit steigender Drehzahl sinkt sowohl der Betrag als auch die Frequenz der induzierten Spannung im Rotor.
  • Der Betrag des Drehmoments sinkt.
  • Drehen sich der Läufer und Ständerfeld mit der gleichen Frequenz, ist die synchrone Drehzahl erreicht.
  • Die Läuferwicklungen sehen keine Änderung des Feldes.
  • Induzierter Strom und Moment der Maschine werden zu Null.
  • Durch Reibungseffekte wird der Rotor wieder abgebremst - es kommt zur erneuten Ausbildung eines Moments.
  • Im Gleichgewichtszustand stellt sich eine Drehzahl knapp unter der synchronen ein.

5 Drehzahl/Drehmomenten-Kennlinie

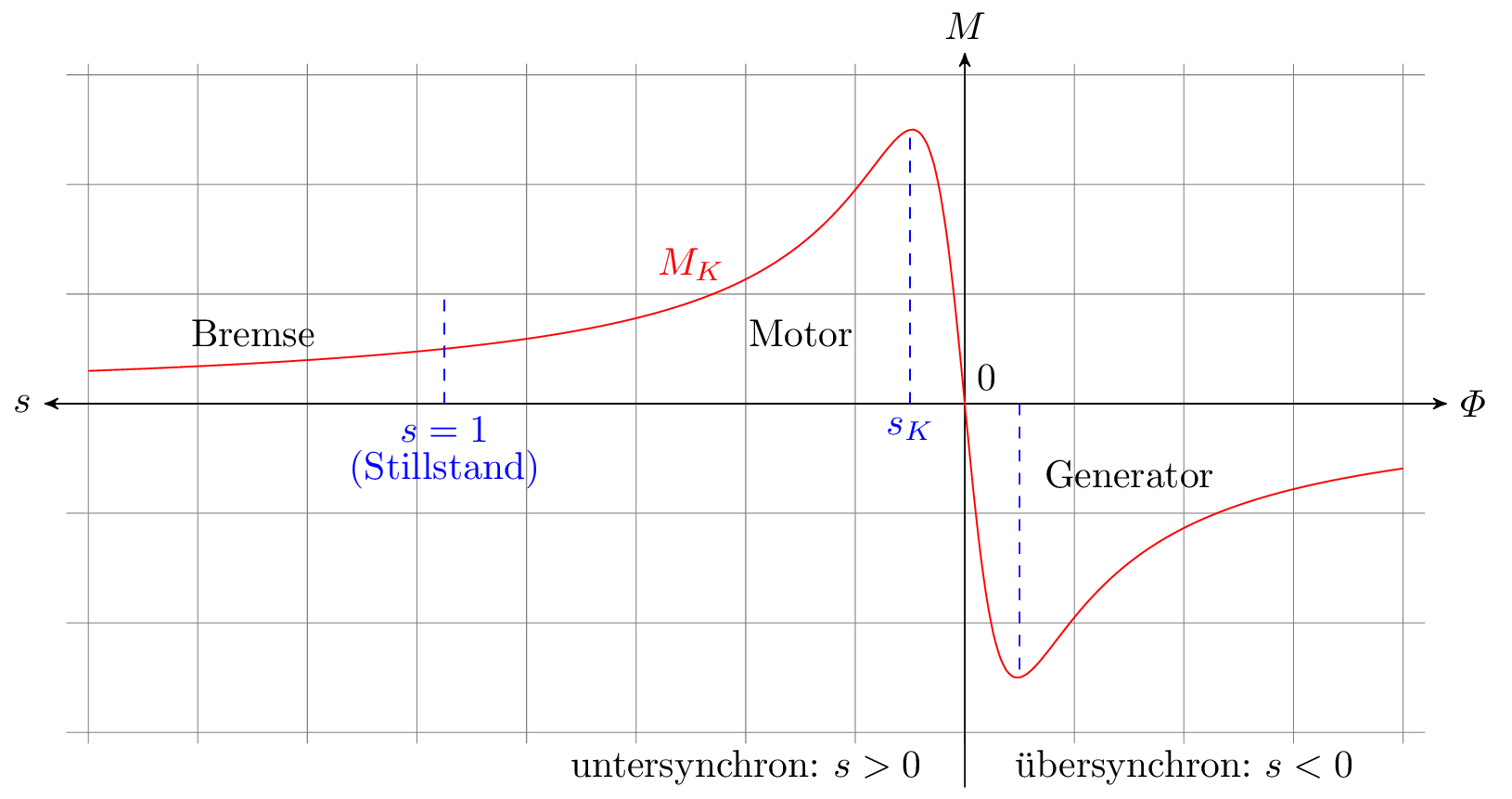
Die Drehzahl/Drehmomenten-Kennlinie ist bei der Asynchronmaschine nichtlinear und kann in mehrere Abschnitte unterteilt werden. Häufig wird die Kennlinie wie in Abbildung 3 gezeigt über den Schlupf \(s\) aufgetragen. Der Schlupf bezeichnet die prozentuale Abweichung der mechanischen Drehgeschwindigkeit des Rotors \(n_\mathrm {r}\) von der elektrischen Drehgeschwindigkeit \(n_\mathrm {s}\) des speisenden Netzes im Stator. \begin {equation} s = \frac {\omega _\mathrm {s} - \omega _\mathrm {r}}{\omega _\mathrm {s}} \end {equation}

Ein Schlupf von \(s=1\) (\(100\%\)) entspricht daher dem Stillstand der Maschine oder Drehzahl \(n=0\), ein Schlupf von \(s=0\) entspricht dem netzsynchronen Betrieb, der jedoch bei der Asynchronmaschine niemals auftreten kann, da das Drehmoment in dem Fall Null wird.

Die Drehzahl/Drehmomenten-Kennlinie wird auch als Klosssche Kennlinie bezeichnet und kann durch die Gleichung 2 ausgedrückt werden: \begin {equation} M = \frac {2\cdot M_\mathrm {K}}{\frac {s_\mathrm {K}}{s} + \frac {s}{s_\mathrm {K}}}\label {GlKloss} \end {equation}

Der Schlupf entspricht bei großen Maschinen in sehr guter Näherung den prozentualen Verlusten der Maschine: \begin {equation} \eta \approx 1-s \end {equation}

PIC

Abbildung 3: Klossche Kennlinie. Drehzahl/Drehmomenten-Kennlinie einer Asynchronmaschine.

Beispiel 1: Asynchronmaschine

Ein Drehstrom-Asynchronmotor hat die folgenden Typenschildangaben:

  • Nennleistung: \(10\,\)kW
  • Nenndrehzahl: \(1440\,\frac {\mathrm {U}}{\mathrm {min}}\)
  • Frequenz: \(50\,\)Hz
  • Kippschlupf: 25%

Berechnen Sie das Nennmoment, das Kippmoment und das Anlaufmoment. \begin {align*} P_\mathrm {N} &= M_\mathrm {N}\cdot \omega _\mathrm {N} = M_\mathrm {N}\cdot 2\pi n_\mathrm {N}\\ M_\mathrm {N} &= \frac {P_\mathrm {N}}{2\pi n_\mathrm {N}} = \frac {10\cdot 10^3\,\mathrm {W}}{2\pi \cdot 1440 \frac {1}{60\,\mathrm {s}}} = 66,31\,\mathrm {Nm}\\ s_\mathrm {N} &= \frac {\omega _\mathrm {s} - \omega _\mathrm {r}}{\omega _\mathrm {s}}\\ &=\frac {2\pi \cdot 1500 \,\frac {1}{60\,\mathrm {s}} - 2\pi \cdot 1440\,\frac {1}{60\,\mathrm {s}}}{2\pi \cdot 1500 \,\frac {1}{60\,\mathrm {s}}}\\ & = 0,04 \end {align*}

Für die Berechnung der weiteren Momente wird Gleichung 2 für die Fälle Nennbetrieb und Stillstand ausgerechnet. \begin {align*} M &= \frac {2\cdot M_\mathrm {K}}{\frac {s_\mathrm {K}}{s} + \frac {s}{s_\mathrm {K}}}\\ M_\mathrm {K} &= \frac {M_\mathrm {N}}{2}\cdot \left (\frac {s_\mathrm {K}}{s_\mathrm {N}} + \frac {s_\mathrm {N}}{s_\mathrm {K}}\right )\\ &= \frac {66,31\,\mathrm {Nm}}{2}\cdot \left (\!\frac {0,25}{0,04} + \frac {0,04}{0,25}\!\right ) = 212,54\,\mathrm {Nm}\\ M_\mathrm {A} &= \frac {2\cdot 212,54\,\mathrm {Nm}}{\frac {0,25}{1} + \frac {1}{0,25}} = 100,02\,\mathrm {Nm} \end {align*}

Expand
×

...