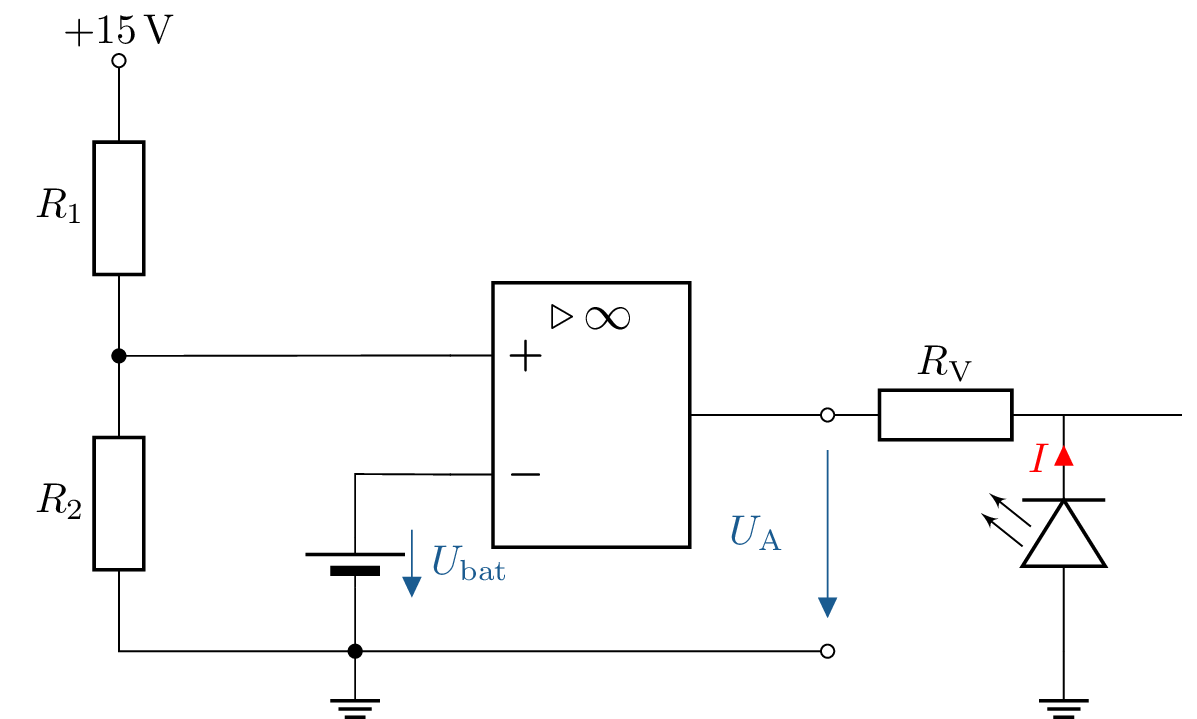
1 Überwachung einer Spannung mit LEDs

Gegeben ist die abgebildete Schaltung, mit dieser soll die Spannung \(U_\mathrm {a}\) überwacht werden. \(U_\mathrm {a}\) darf dabei nur im folgenden Bereich liegen \(\mathrm {4,75\,V} < U_\mathrm {a} < \mathrm {5,25\,V}\). Wenn die Spannung über oder unterschritten ist, soll jeweils eine der LEDs aufleuchten. Erzgänzen Sie die Schaltung.

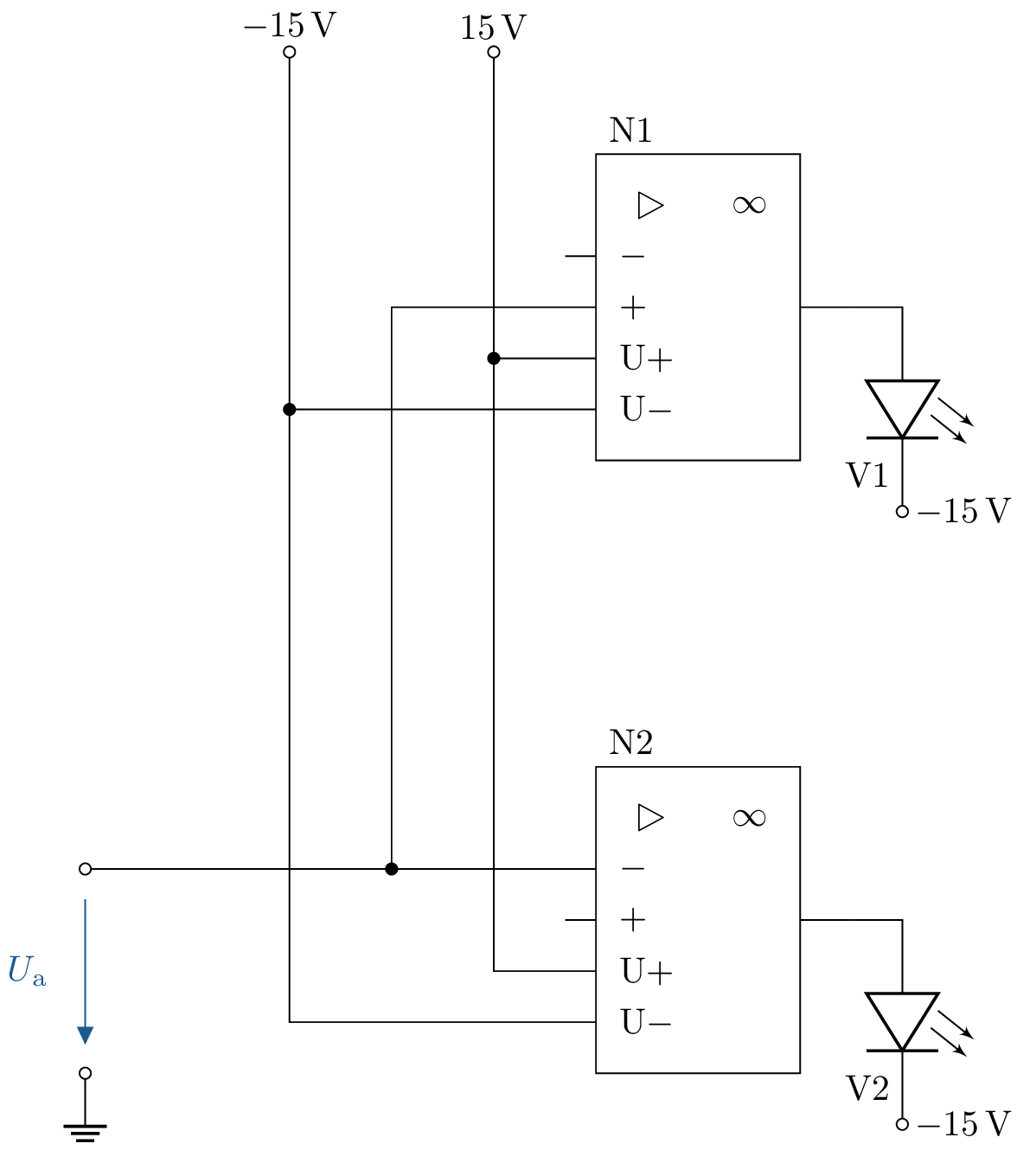
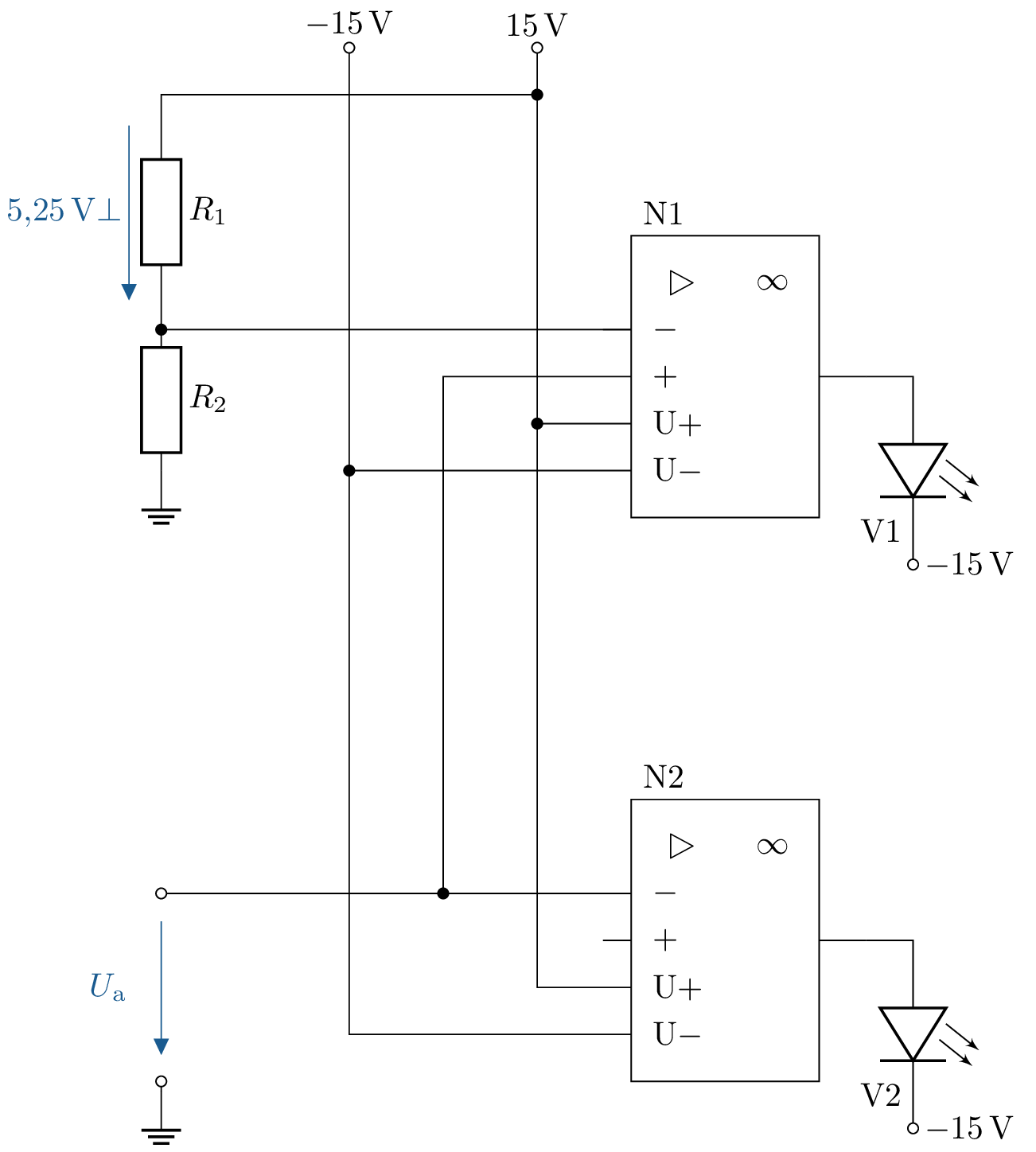
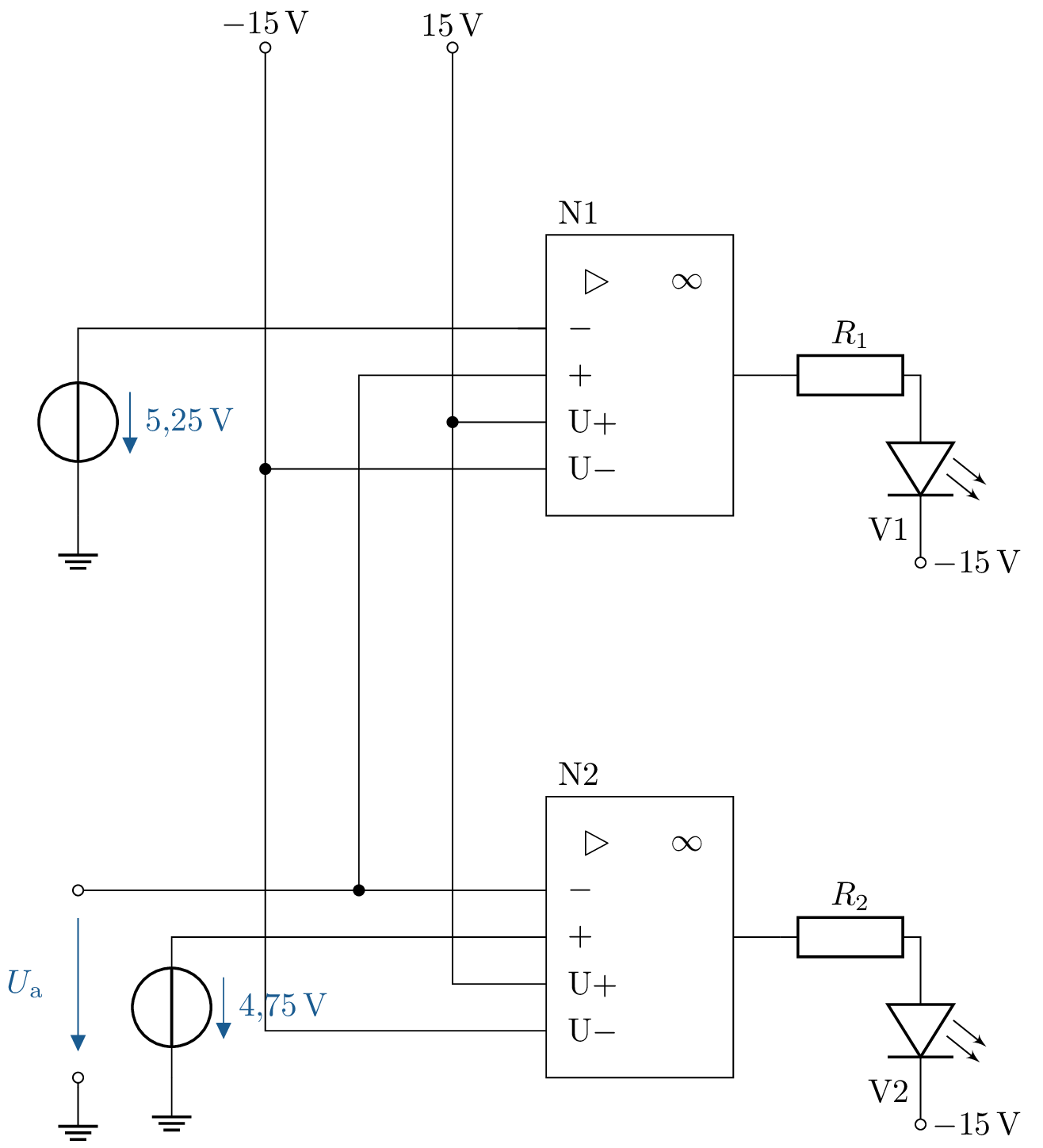
1.1 Lösung:

\begin {equation*} \begin {aligned} \frac {U_1}{U_0} &= \frac {R_1}{R_1 + R_2} \\ \frac {U_1 \cdot (R_1 + R_2)}{U_0} &= R_1 \\ U_1\cdot (R_1+R_2) &= R_1 \cdot U_0 \\ U_1\cdot R_1 + U_1\cdot R_2 &= R_1 \cdot U_0 \\ U_1\cdot R_1 &= R_1 \cdot U_0 - U_1\cdot R_2 \\ U_1\cdot R_2 &= R_1 \cdot (U_0 - U_1) \\ \frac {U_1 \cdot R_2}{U_0 - U_1} &= R_1 \end {aligned} \end {equation*}

\[ R_1 = 268.96 \, \Omega \]

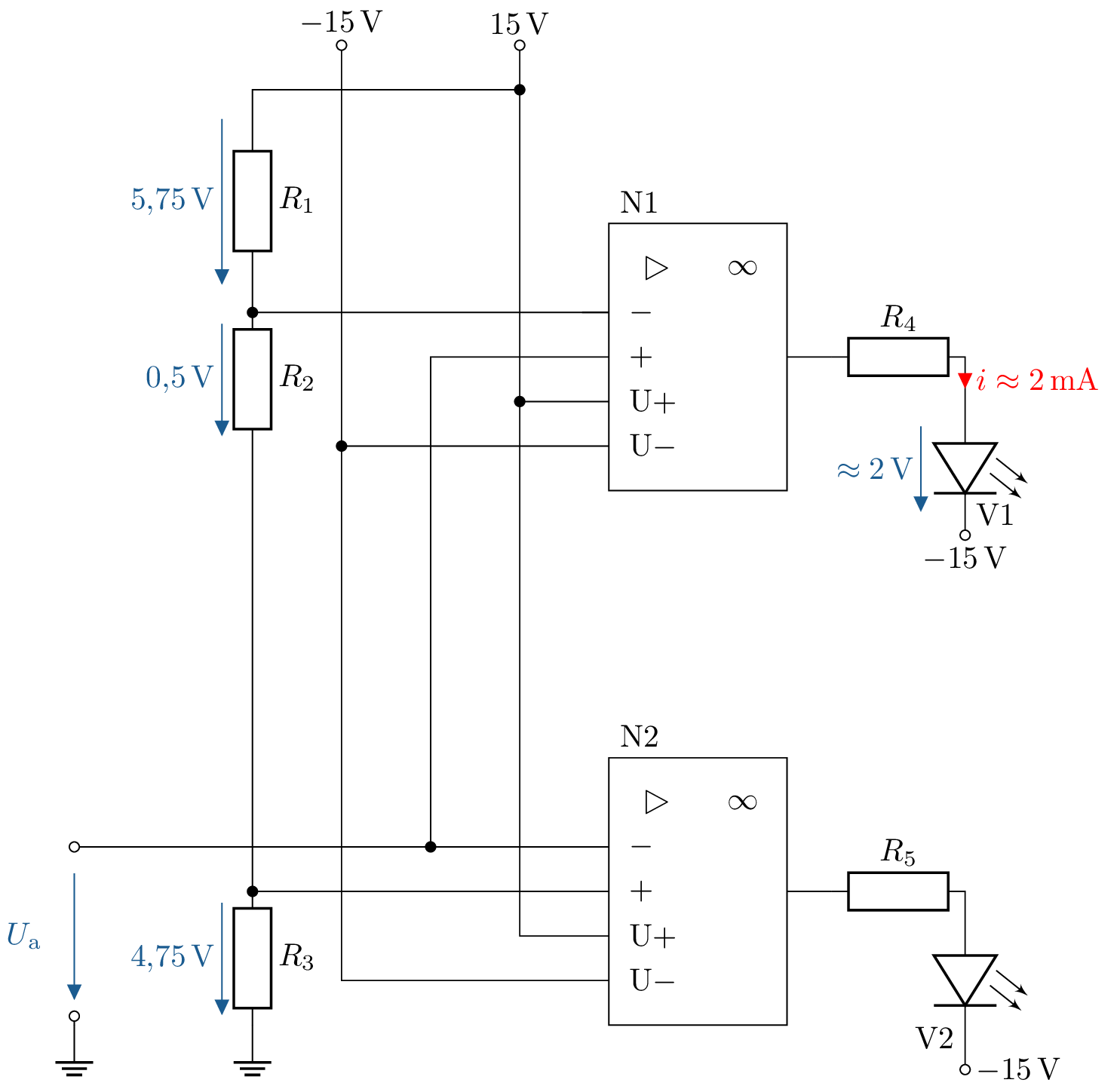
\begin {align*} R_1 &= 3.75 \,\text {k}\Omega \\ R_2 &= 500 \,\Omega \\ R_3 &= 4.75 \,\text {k}\Omega \\ R_4 &= \frac {28 \, \mathrm {V}}{20 \, \mathrm {mA}} \approx 1,4 \,\text {k}\Omega \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

2 Widerstandsberechnung für nicht-invertierenden Verstärker

Gegeben ist die abgebildete Schaltung mit einem nichtinvertierenden Verstärker. Dabei ist der Widerstand \(R_\mathrm {2} = 1\,\mathrm {k \Omega }\). Was für Widerstandswerte muss \(R_\mathrm {1}\) aufweisen, damit die Verstärkung der gegebenen Schaltung 10, 50 und 100 beträgt?

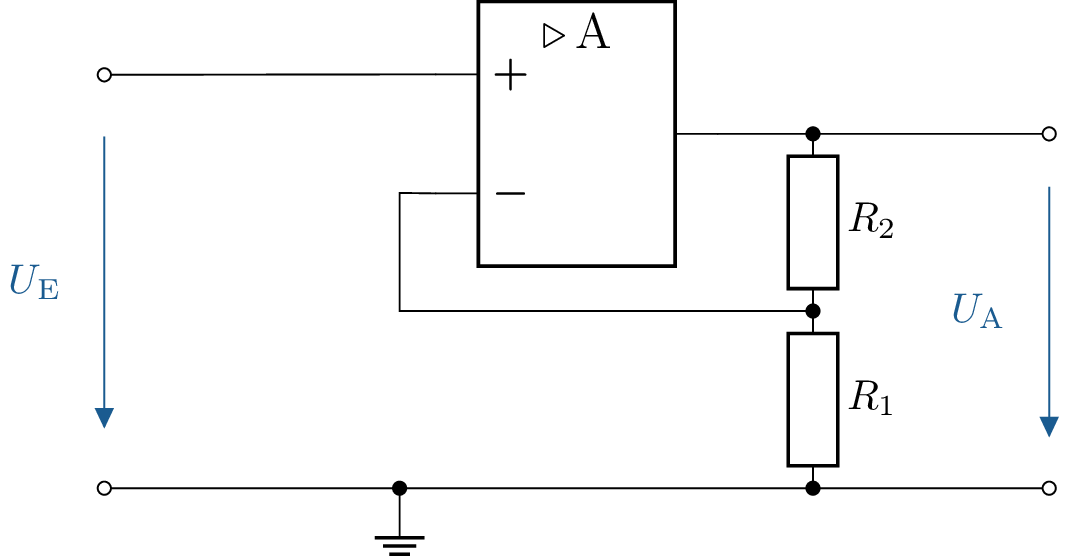
2.1 Lösung:

Gemäß Formel nichtinvertierender Verstärker: \begin {align*} V = 1 + \frac {R_\mathrm {1}}{R_\mathrm {2}} \end {align*}

Formel nach \(R_1\) umstellen: \begin {align*} R_1 = R_2 \cdot (V - 1) \end {align*}

• \(V = 10\) \begin {align*} R_1 = \mathrm {1\,k\Omega \cdot (10 - 1) = 9\,k\Omega } \end {align*}
• \(V = 50\) \begin {align*} R_1 = \mathrm {1\,k\Omega \cdot (50 - 1) = 49\,k\Omega } \end {align*}
• \(V = 100\) \begin {align*} R_1 = \mathrm {1\,k\Omega \cdot (100 - 1) = 99\,k\Omega } \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

3 Widerstandsberechnung für invertierenden Verstärker

Gegeben ist die abgebildete Schaltung mit einem invertierenden Verstärker. Dabei ist der Widerstand \(R_\mathrm {2} = 1\,\mathrm {k \Omega }\). Was für Widerstandswerte muss \(R_\mathrm {1}\) aufweisen, damit die Verstärkung der gegebenen Schaltung -10, -50 und -100 beträgt?

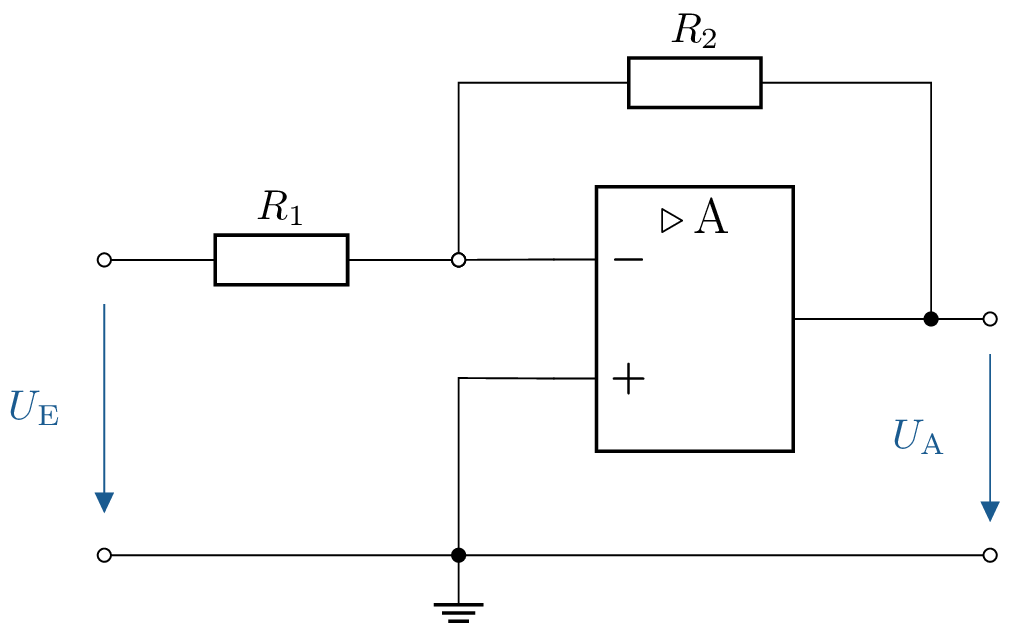
3.1 Lösung:

Gemäß Formel invertierender Verstärker: \begin {align*} V = - \frac {R_2}{R_1} \end {align*}

Formel umstellen nach \(R_\mathrm {1}\): \begin {align*} R_1 = - \frac {R_2}{V} \end {align*}

• \(V = - 10\) \begin {align*} R_1 =\mathrm {- \frac {1\,k\Omega }{- 10} = 100\,\Omega } \end {align*}
• \(V = - 50\) \begin {align*} R_1 =\mathrm {- \frac {1\,k\Omega }{- 50} = 20\,\Omega } \end {align*}
• \(V = - 100\) \begin {align*} R_1 =\mathrm {- \frac {1\,k\Omega }{- 100} = 10\,\Omega } \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

4 Berechnung der Ausgangsspannung bei zwei Eingangsspannungen

Gegeben ist die abgebildete Schaltung mit einem idealen Operationsverstärker. Dabei ist der Widerstand \(R_\mathrm {1} = \mathrm {100\,k\Omega }\) und \(R_2=\mathrm {10\,k\Omega }\). Die Betriebsspannung beträgt \(\mathrm {\pm 15\,V}\).

• Ermitteln Sie die Ausgangsspannung \(U_\mathrm {A}\) bei \(U_\mathrm {E}=2\,\mathrm {mV}\) und \(U_\mathrm {bat} = \mathrm {0\,V}\)
• Ermitteln Sie die Ausgangsspannung \(U_\mathrm {A}\) bei \(U_\mathrm {E}=20\,\mathrm {mV}\) und \(U_\mathrm {bat}=\mathrm {0\,V}\)

4.1 Lösung:

Verstärkung berechnen: \begin {align*} V =\mathrm {- \frac {100\,k\Omega }{10\,k\Omega } = -10} \end {align*}

Formel für Verstärkung: \begin {align*} V = \frac {U_\mathrm {A}}{U_\mathrm {E}} \end {align*}

Formel umstellen nach \(U_\mathrm {A}\): \begin {align*} U_\mathrm {A} = V \cdot U_\mathrm {E} \end {align*}

• \begin {align*} U_\mathrm {A} = \mathrm {-10 \cdot 2\,mV = -20\,mV} \end {align*}
• \begin {align*} U_\mathrm {A} = \mathrm {-10 \cdot 20\,mV = -200\,mV} \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

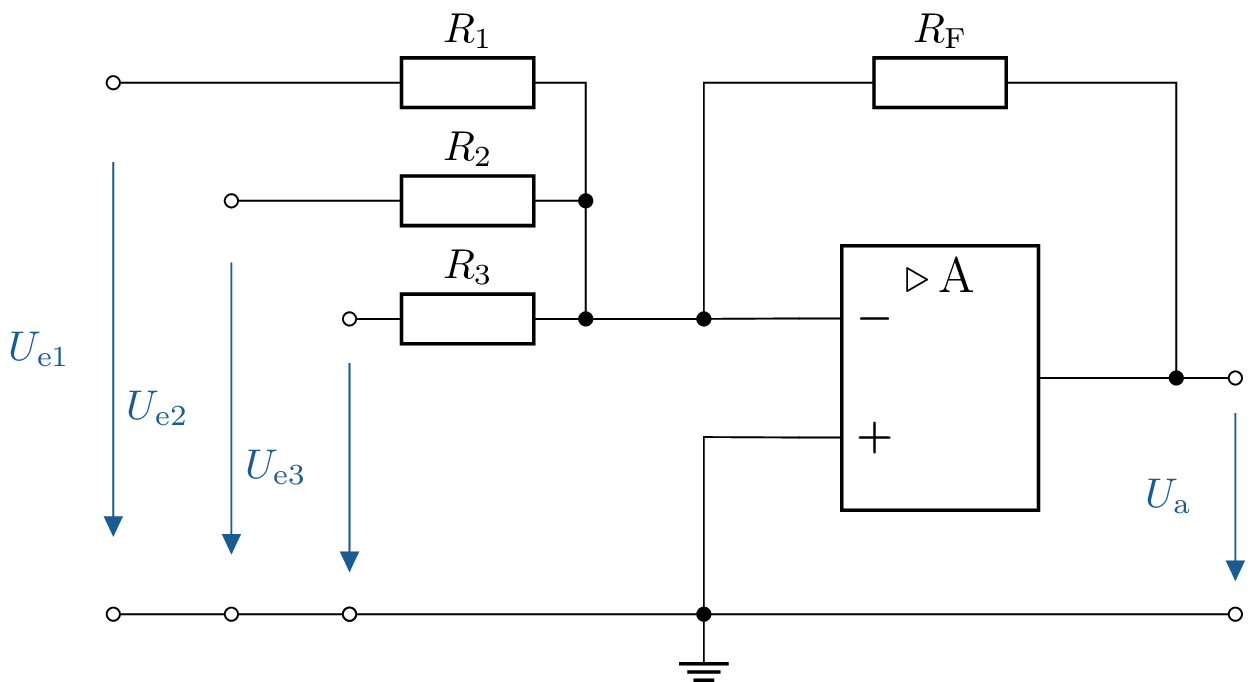
5 Berechnung der Ausgangsspannung bei mehreren Eingangsspannungen

Gegeben ist die abgebildete Schaltung mit einem idealen Operationsverstärker. Die Betriebsspannung beträgt \(\mathrm {\pm 15\,V}\).

• Die Widerstände sind alle gleich, es gilt \(R_1 = R_2 = R_3 = R_\mathrm {F} = 10\,\mathrm {k\Omega }\). Die Spannungen sind \(U_\mathrm {E1} = \mathrm {1\,V}\), \(U_\mathrm {E2} = \mathrm {2\,V}\), \(U_\mathrm {E3} = \mathrm {3\,V}\). Wie hoch ist die Spannung am Ausgang \(U_\mathrm {A}\)?
• Die Eingangsspannungen bleiben gleich groß, nur die Widerstände betragen nun \(R_\mathrm {F} = \mathrm {10\,k\Omega }\), \(R_\mathrm {1} = \mathrm {2\,k\Omega }\), \(R_\mathrm {2} = \mathrm {5\,k\Omega }\), \(R_\mathrm {3} = \mathrm {10\,k\Omega }\). Wie hoch ist die Spannung am Ausgang \(U_\mathrm {A}\)?
• Die Eingangsspannungen bleiben gleich groß, nur die Widerstände betragen nun \(R_\mathrm {F} = \mathrm {10\,k\Omega }\), \(R_\mathrm {1} = \mathrm {10\,k\Omega }\), \(R_\mathrm {2} = \mathrm {5\,k\Omega }\), \(R_\mathrm {3} = \mathrm {2\,k\Omega }\). Wie hoch ist die Spannung am Ausgang \(U_\mathrm {A}\)?

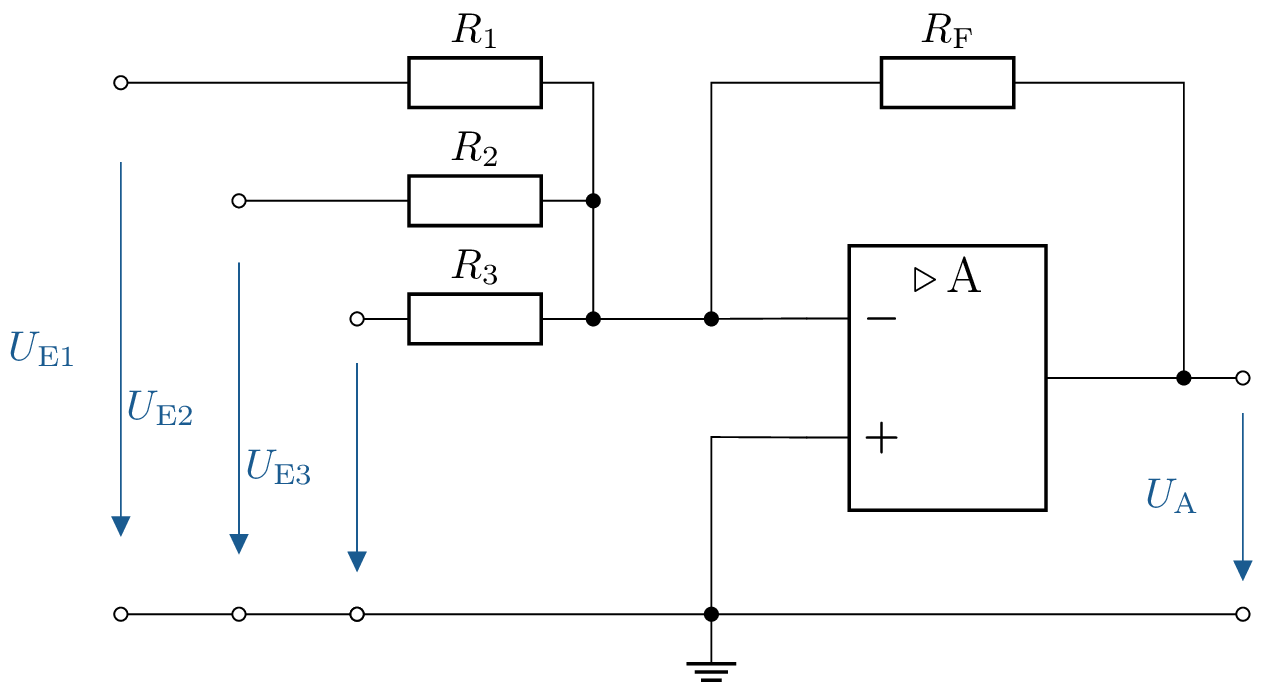
5.1 Lösung:

Formel: \begin {align*} U_\mathrm {A} = - (U_\mathrm {E1} \cdot \frac {R_\mathrm {F}}{R_1} + U_\mathrm {{E2}} \cdot \frac {R_\mathrm {F}}{R_2} + U_\mathrm {E3} \cdot \frac {R_\mathrm {F}}{R_3}) \end {align*}

• \begin {align*} U_\mathrm {A} =\mathrm {- (1\,V \cdot \frac {10\,k\Omega }{10\,k\Omega } + 2\,V \cdot \frac {10\,k\Omega }{10\,k\Omega } + 3\,V \cdot \frac {10\,k\Omega }{10\,k\Omega }) = -6\,V} \end {align*}
• \begin {align*} U_\mathrm {A} =\mathrm { - (1\,V \cdot \frac {10\,k\Omega }{2\,k\Omega } + 2\,V \cdot \frac {10\,k\Omega }{5\,k\Omega } + 3\,V \cdot \frac {10\,k\Omega }{10\,k\Omega }) = -12\,V} \end {align*}

• \begin {align*} U_\mathrm {A} =\mathrm { - (1\,V \cdot \frac {10\,k\Omega }{10\,k\Omega } + 2\,V \cdot \frac {10\,k\Omega }{5\,k\Omega } + 3\,V \cdot \frac {10\,k\Omega }{2\,k\Omega }) = -20\,V} \end {align*}

  Anmerkung: \(-20\,\mathrm {V}\) nicht möglich, da die Betriebsspannung \(\mathrm {\pm 15\,V}\) beträgt. Dies führt dazu, dass der niedrigste Wert \(\mathrm {-15\,V}\) sein kann.

Siehe: Abschnitt ?? und Tabelle ??

6 Berechnung der Ausgangsspannung einer zweistufigen OPV-Schaltung

Berechnen Sie \(U_\mathrm {A}\) mit den folgenden Werten:
\(R_1 = \mathrm {10\,k\Omega }\), \(R_2 = \mathrm {20\,k\Omega }\), \(R_3 = \mathrm {30\,k\Omega }\), \(R_4 = \mathrm {10\,k\Omega }\), \(R_5 = \mathrm {20\,k\Omega }\)

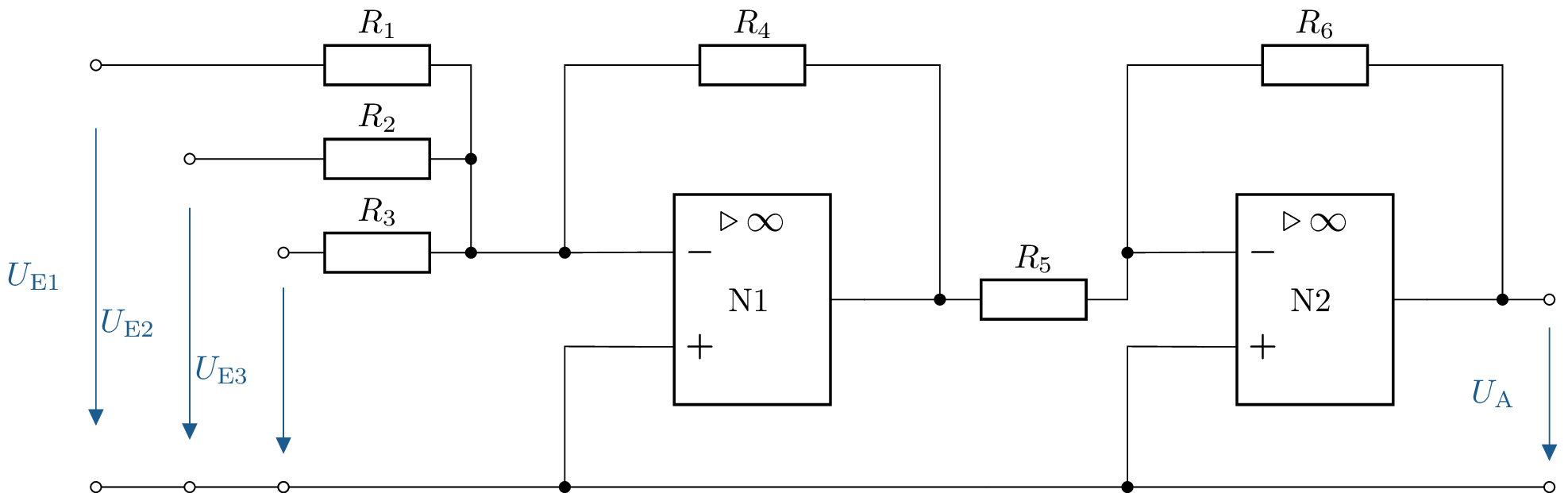
6.1 Lösung:

Formel: \begin {align*} U_\mathrm {N1} = - \left ( \frac {R_\mathrm {N}}{R_\mathrm {1}} U_\mathrm {E1} + \frac {R_\mathrm {N}}{R_2} U_\mathrm {E2} + \frac {R_\mathrm {N}}{R_\mathrm {3}} U_\mathrm {E3} \right ) \end {align*}

\begin {align*} U_\mathrm {A} = -\frac {R_\mathrm {6}}{R_\mathrm {5}} U_\mathrm {N1} \end {align*}

Berechnung:

Berechnung von \(U_\mathrm {N1}\) \begin {align*} U_\mathrm {N1} &= - \left ( \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } U_\mathrm {E1} + \frac {10\,\mathrm {k}\Omega }{20\,\mathrm {k}\Omega } U_\mathrm {E2} + \frac {10\,\mathrm {k}\Omega }{30\,\mathrm {k}\Omega } U_\mathrm {E3} \right ) \\ &= - \left ( U_\mathrm {E1} + 0,5 U_\mathrm {E2} + \frac {1}{3} U_\mathrm {E3} \right ) \end {align*}

Berechnung von \(U_\mathrm {A}\) \begin {align*} U_\mathrm {A} &= -2 \cdot U_\mathrm {N1} \\ &= -2 \left ( - \left ( U_\mathrm {E1} + 0,5 U_\mathrm {E2} + \frac {1}{3} U_\mathrm {E3} \right ) \right ) \\ &= 2 \left ( U_\mathrm {E1} + 0,5 U_\mathrm {E2} + \frac {1}{3} U_\mathrm {E3} \right ) \end {align*}

Die Ausgangsspannung \(U_\mathrm {A}\) beträgt: \begin {align*} U_\mathrm {A} &= 2 U_\mathrm {E1} + U_\mathrm {E2} + \frac {2}{3} U_\mathrm {E3} \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

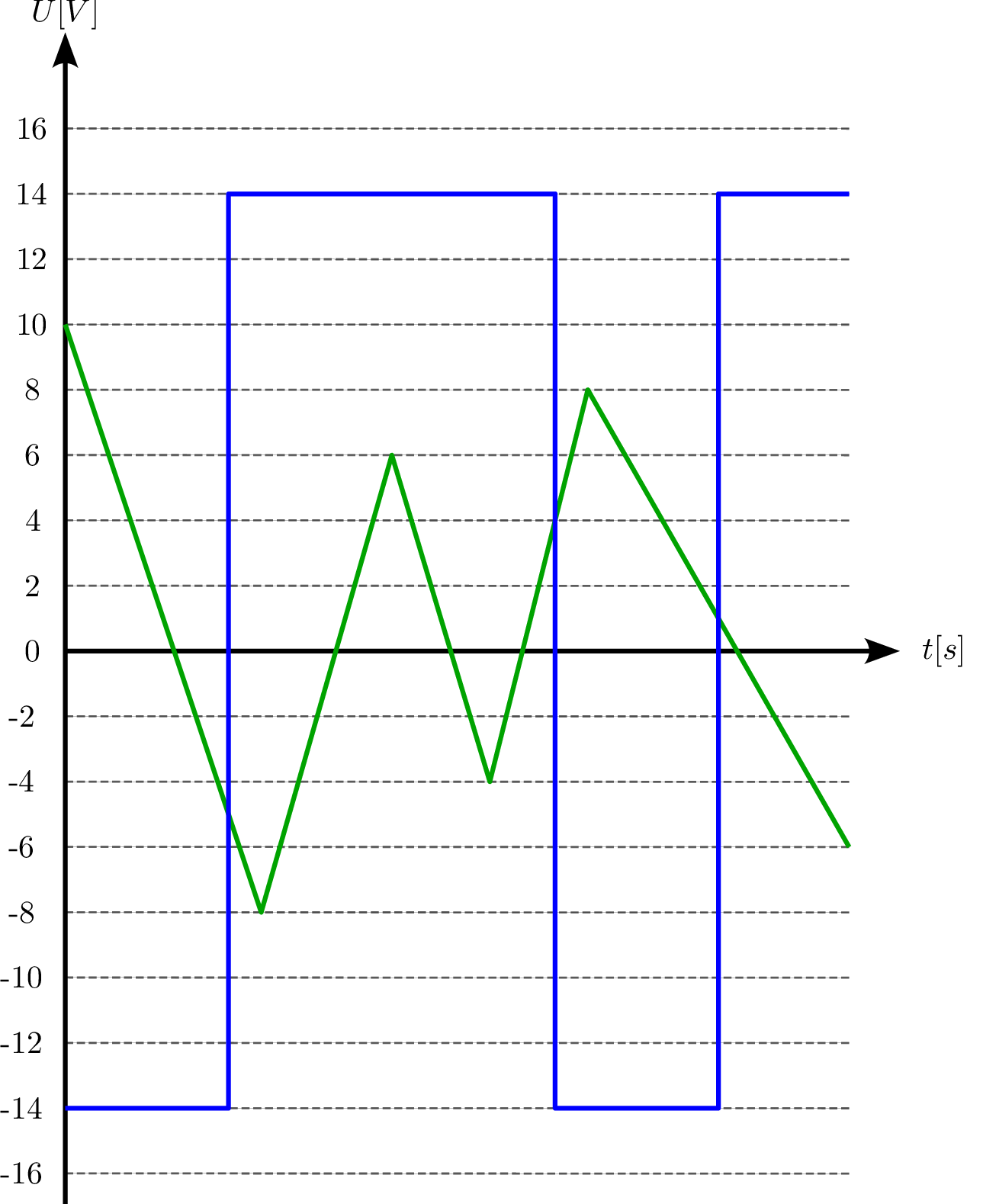
7 Dimensionierung einer Komparatorschaltung mit Diode

Dimensionieren Sie die Beschaltung des Komparators so, dass das unten skizzierte Übertragungsverhalten (grün: \(U_\mathrm {E}\), blau: \(U_\mathrm {A}\)) entsteht. Die Durchlassspannung der Diode wird mit \(U_\mathrm {D} = \mathrm {0,7\,V}\) angenommen. Die maximale Verlustleistung des Widerstandes beträgt 1/4 W.

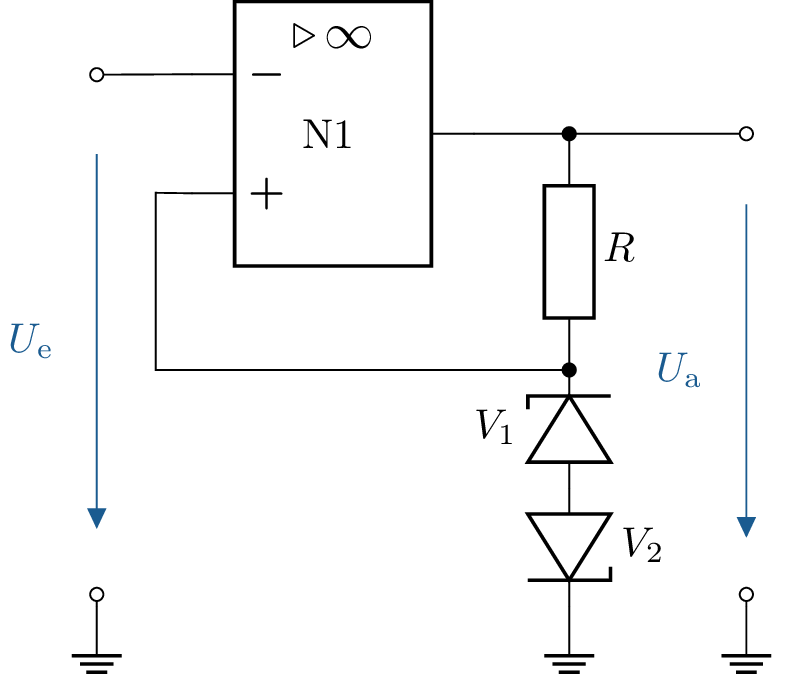
7.1 Lösung:

Formel: \begin {align*} P_\mathrm {R} = \frac {U_\mathrm {R}^2}{R} \end {align*}

Spannung am Widerstand \(R\): \begin {align*} U_\mathrm {R} &= U_\mathrm {a} - U_\mathrm {D} \\ &= 14\,\mathrm {V} - 0,7\,\mathrm {V} \\ &= 13,3\,\mathrm {V} \end {align*}

Berechnung des Widerstands \(R\): \begin {align*} P_\mathrm {R} &= \frac {U_\mathrm {R}^2}{R} \leq \frac {1}{4}\,\mathrm {W} \\ R &= \frac {U_R^2}{P_{\text {max}}} = \frac {(13,3\,\mathrm {V})^2}{0,25\,\mathrm {W}} = \frac {176,89\,\mathrm {V}^2}{0,25\,\mathrm {W}} = 707,56\,\Omega \end {align*}

Normierter Widerstandswert: \begin {align*} R &= 710\,\Omega \end {align*}

Überprüfung der Verlustleistung: \begin {align*} P_\mathrm {R} &= \frac {(13,3\,\mathrm {V})^2}{710\,\Omega } \approx 0,25\,\mathrm {W} \end {align*}

Der Widerstand \(R\) sollte den Wert: \begin {align*} R &= 710\,\Omega \end {align*}

haben, um die maximale Verlustleistung nicht zu überschreiten und das gewünschte Übertragungsverhalten zu gewährleisten. Siehe: Abschnitt ?? und Tabelle ??

8 Beschreibung von idealen Eigenschaften

Beschreiben Sie folgende Kennzeichen eines idealen Operationsverstärkers:

• Eingangswiderstand
• Ausgangswiderstand
• Differenzverstärkung
• Eingangsoffsetspannung

8.1 Lösung:

• Eingangswiderstand: unendlich, um die Spannungsquelle wenig zu belasten
• Ausgangswiderstand: \(0\,\Omega \), da OP so viel Leistung wie möglich abgeben soll
• Differenzverstärkung: unendlich, um kleine Signale zu verstärken
• Eingangsoffsetspannung: \(0\,\mathrm {V}\), damit OP bei keinem Eingangssignal auch keine Ausgangsspannung ausgibt

Siehe: Tabelle ??

9 Ausgangsspannung eines Komparators ermitteln

Geben ist der dargestellte Komparator. Die Spannung \(U_\mathrm {1}= \mathrm {8,25\,V}\) sei konstant. Wie groß ist die Ausgangsspannung für \(U_2 = \mathrm {0\,V; 4\,V; 8\,V; 8,2\,V; 8,249\,V; 8,251\,V; 8,3\,V; 10\,V}\)?

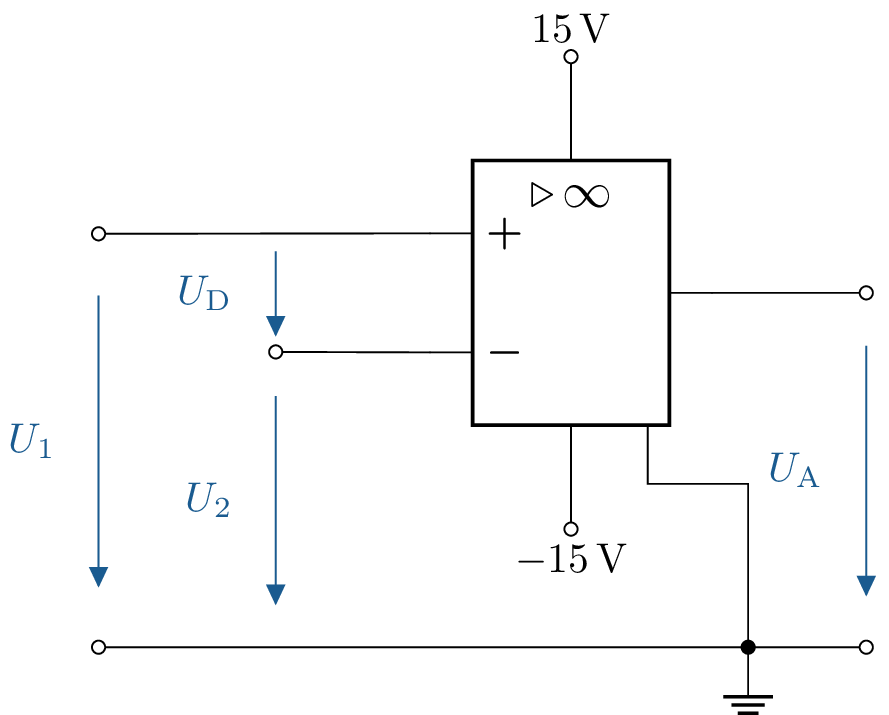
9.1 Lösung:

Ausnutzung der Maschenregel besagt: \begin {align*} -U_1 + U_2 + U_D &= 0 \\ U_\mathrm {D} &= U_1 - U_2 \end {align*}

• \(U_2 = 0\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 0\,V = 8,25\,V}\\ U_\mathrm {A} &= \mathrm {13,5\,V} \end {align*}
• \(U_2 = 4\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 4\,V = 4,25\,V}\\ U_\mathrm {A} &= \mathrm {13,5\,V} \end {align*}
• \(U_2 = 8\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 8\,V = 0,25\,V}\\ U_\mathrm {A} &= \mathrm {13,5\,V} \end {align*}
• \(U_2 = 8,2\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 8,2\,V = 0,05\,V}\\ U_\mathrm {A} &= \mathrm {8\,V} \end {align*}
• \(U_2 = 8,249\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 8,249\,V = 1\,mV}\\ U_\mathrm {A} &= \mathrm {4\,V} \end {align*}
• \(U_2 = 8,251\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 8,251\,V = -1\,mV}\\ U_\mathrm {A} &= \mathrm {-4\,V} \end {align*}
• \(U_2 = 8,3\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 8,3\,V = -0,05\,V}\\ U_\mathrm {A} &= \mathrm {-8\,V} \end {align*}
• \(U_2 = 10\,V\) \begin {align*} U_\mathrm {D} &= \mathrm { 8,25\,V - 10\,V = -1,75\,V}\\ U_\mathrm {A} &= \mathrm {-13,5\,V} \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

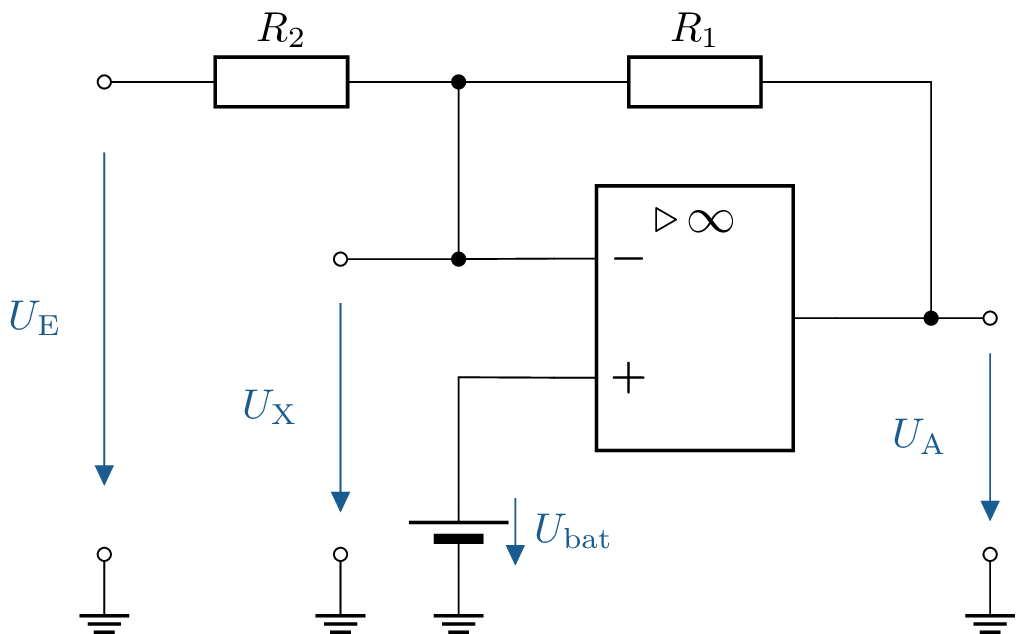
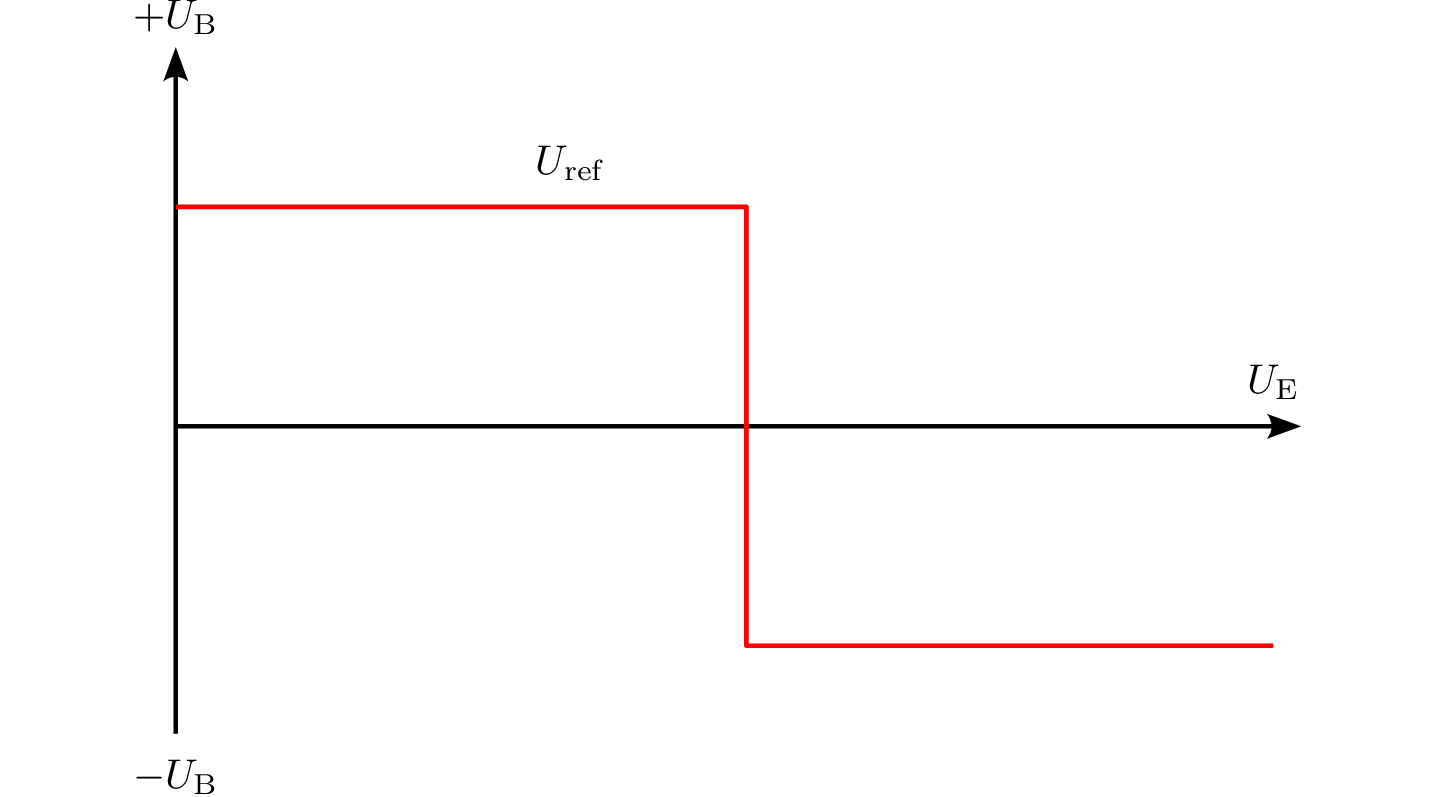
10 Komparatorschaltung zur Akku-Überwachung berechnen

Zur Überwachung des Ladezustandes eines Akkus soll ein Komparator eingesetzt werden. Der Komparator soll umschalten, wenn eine Batteriespannung \(U_\mathrm {bat}\) von \(6\,\mathrm {V}\) unterschritten wird. Der Widerstand \(R_1\) beträgt \(10\,\mathrm {k\Omega }\). Die Betriebsspannung des Komparators beträgt \(\pm 15\,\mathrm {V}\).

• Wie groß muss der Widerstand \(R_2\) gewählt werden?
• Zur Anzeige des Ladezustands soll eine LED verwendet werden. Erweitern Sie die Schaltung um die Ladungsanzeige per LED.
• Durch die LED mit der Flussspannung von 2,2 V darf maximal ein Strom von 20 mA fließen. Wie groß muss der Vorwiderstand gewählt werden?
• Die Spannung am Spannungsteiler ist abhängig von der Betriebsspannung. Welche anderen geeigneten Bauelemente existieren für die Erzeugung der Referenzspannung? Nennen und zeichnen Sie ein Beispiel.

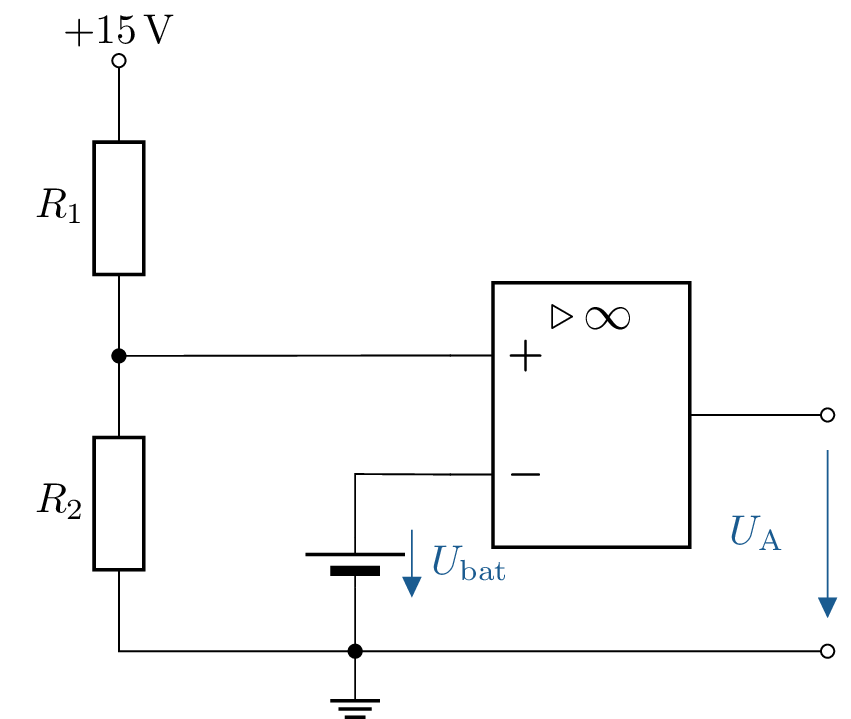
10.1 Lösung:

• Berechnung des Widerstands \(R_2\)

  Der Komparator soll umschalten, wenn die Batteriespannung \(U_{\text {bat}}\) unter \(6\,\mathrm {V}\) fällt. Das Verhältnis der Widerstände \(R_1\) und \(R_2\) im Spannungsteiler muss so gewählt werden, dass am nicht-invertierenden Eingang die Referenzspannung \(U_{\text {ref}} = 6\,\mathrm {V}\) anliegt: \[ U_{\text {ref}} = \frac {R_2}{R_1 + R_2} \cdot U_\mathrm {B} \] mit \(U_\mathrm {B} = 15\,\mathrm {V}\) und \(R_1 = 10\,\mathrm {k}\Omega \). Einsetzen: \[ 6\,\mathrm {V} = \frac {R_2}{10\,\mathrm {k}\Omega + R_2} \cdot 15\,\mathrm {V} \] Umstellen nach \(R_2\): \[ R_2 = \frac {6\,\mathrm {V} \cdot 10\,\mathrm {k}\Omega }{15\,\mathrm {V} - 6\,\mathrm {V}} = 6,66\,\mathrm {k}\Omega \]

• Erweiterung der Schaltung um eine LED-Anzeige:

  Die LED soll anzeigen, wenn die Batteriespannung unter \(6\,\mathrm {V}\) fällt. Dazu wird die LED mit Vorwiderstand \(R_V\) an den Ausgang des Komparators geschaltet.

• Schaltverhalten der Schaltung:

  • Leere Batterie (\(U_{\text {bat}} = 5\,\mathrm {V}\)): \begin {align*} U_+ &= 6\,\mathrm {V} - U_{\text {bat}} \\ U_+ &= 6\,\mathrm {V} - 5\,\mathrm {V} = 1\,\mathrm {V} \end {align*}

    Da \(U_+ < U_{\text {ref}}\), schaltet der Komparator um: \[ U_\mathrm {A} = -15\,\mathrm {V} \] Die LED leuchtet.

  • Volle Batterie (\(U_{\text {bat}} = 7\,\mathrm {V}\)): \begin {align*} U_+ &= 6\,\mathrm {V} - U_{\text {bat}} \\ U_+ &= 6\,\mathrm {V} - 7\,\mathrm {V} = -1\,\mathrm {V} \end {align*}

    Da \(U_+ > U_{\text {ref}}\), schaltet der Komparator: \[ U_\mathrm {A} = 15\,\mathrm {V} \] Die LED bleibt aus.

• Dimensionierung des Vorwiderstands \(R_\mathrm {V}\)

  Gegeben:

  • Flussspannung der LED: \(U_\mathrm {F} = 2,2\,\mathrm {V}\)
  • Strom durch die LED: \(I_\mathrm {F} = 20\,\mathrm {mA}\)
  • Ausgangsspannung des Komparators: \(U_\mathrm {A} = -15\,\mathrm {V}\)

  Der Vorwiderstand \(R_\mathrm {V}\) berechnet sich aus: \[ R_\mathrm {V} = \frac {-U_\mathrm {A} - U_\mathrm {F}}{I_\mathrm {F}} \] Einsetzen der Werte: \[ R_\mathrm {V} = \frac {-(-15\,\mathrm {V}) - 2,2\,\mathrm {V}}{20\,\mathrm {mA}} = \frac {12,8\,\mathrm {V}}{0,02\,\mathrm {A}} = 640\,\Omega \]

  Für einen sicheren Betrieb der LED wird Widerstandswert von mindestens \(R_\mathrm {V} = 640\,\Omega \) benötigt.

• Alternative Spannungsreferenz:

  Da die Spannung des Spannungsteilers abhängig von der Betriebsspannung ist, könnte eine Zener-Diode als Referenzelement verwendet werden. Eine Zener-Diode stellt eine konstante Referenzspannung unabhängig von Schwankungen der Versorgungsspannung bereit.

• Beispiel-Schaltung:

  • Die Zener-Diode wird mit einem Vorwiderstand an die Betriebsspannung \(+15\,\mathrm {V}\) angeschlossen.
  • Die Referenzspannung wird direkt von der Kathode der Zener-Diode abgegriffen.

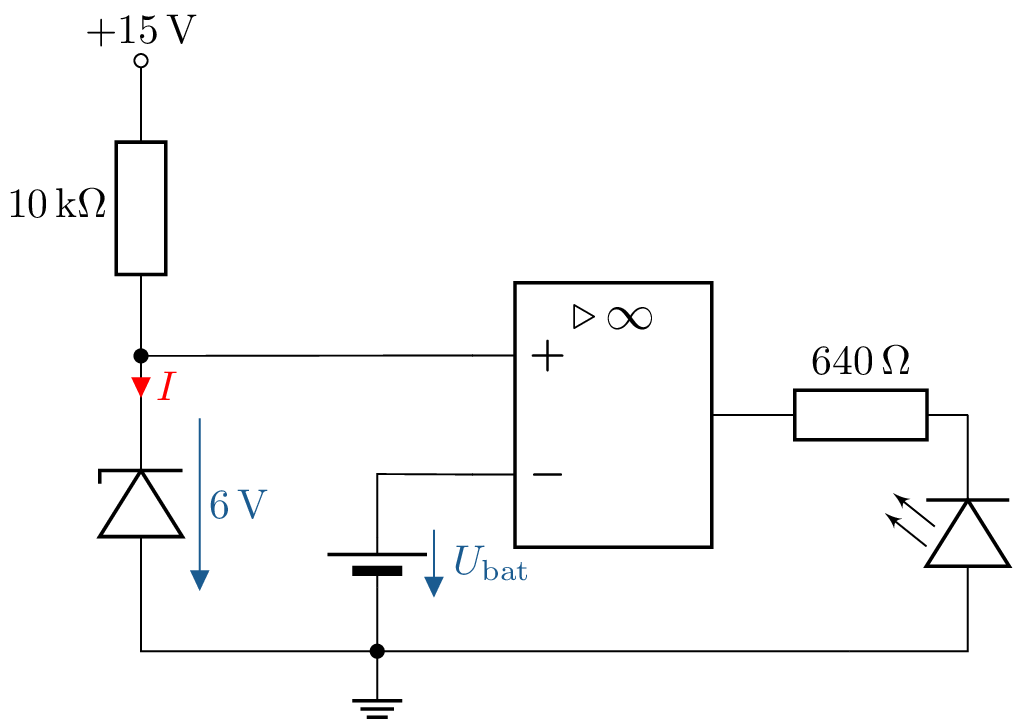
Siehe: Abschnitt ?? und Tabelle ??

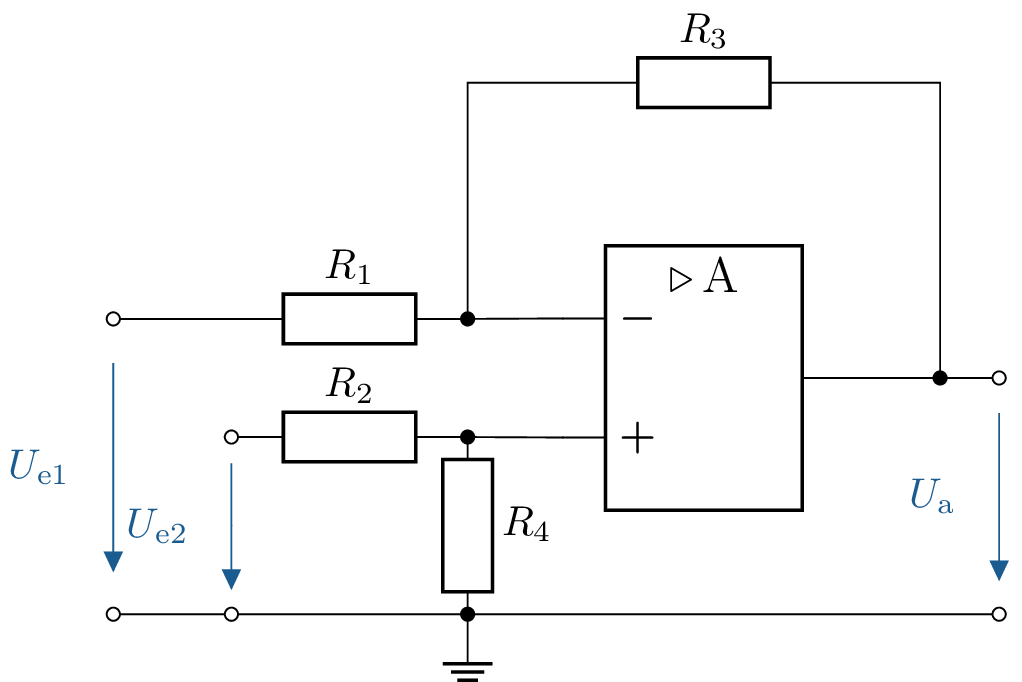
11 Schaltungsentwurf eines Operationsverstärkers mit zwei Eingangsspannungen

Zwischen der Ausgangsspannung \(U_\mathrm {a}\) und den Eingangsspannungen \(U_\mathrm {1}\) und \(U_\mathrm {2}\) besteht der folgende funktionale Zusammenhang: \(U_\mathrm {a} = -5 \ U_\mathrm {1} - 0,8 \ U_\mathrm {2}\). Geben Sie eine mit Operationsverstärker(n) und Widerständen aufgebaute Schaltung zur Realisierung dieses funktionalen Zusammenhangs an. Die Operationsverstärker dürfen als ideale Operationsverstärker angenommen werden. Geben Sie Werte der verwendeten Widerstände an!

11.1 Lösung:

Der gegebene funktionale Zusammenhang zwischen der Ausgangsspannung \(U_\mathrm {a}\) und den Eingangsspannungen \(U_1\) und \(U_2\) lautet: \( U_\mathrm {a} = -5 U_1 - 0,8 U_2 \)

1. Schaltungsbeschreibung

Zur Realisierung dieses Zusammenhangs nutzen wir eine Summierschaltung mit einem invertierenden Operationsverstärker. Die Ausgangsspannung des invertierenden Summierers lautet: \( U_\mathrm {a} = -\left ( \frac {R_\mathrm {F}}{R_1} U_1 + \frac {R_\mathrm {F}}{R_2} U_2 \right ) \) Vergleich mit der Vorgabe: \( - \left ( \frac {R_\mathrm {F}}{R_1} \right ) = -5 \Rightarrow \frac {R_\mathrm {F}}{R_1} = 5 \) \( - \left ( \frac {R_\mathrm {F}}{R_2} \right ) = -0,8 \Rightarrow \frac {R_\mathrm {F}}{R_2} = 0,8 \)

2. Wahl der Widerstandswerte

Wir setzen \(R_\mathrm {F} = 10\,\mathrm {k}\Omega \) (typischer Wert im Bereich 1–100 k\(\Omega \)):

• Berechnung von \(R_1\): \( \frac {R_\mathrm {F}}{R_1} = 5 \Rightarrow R_1 = \frac {R_\mathrm {F}}{5} = \frac {10\,\mathrm {k}\Omega }{5} = 2\,\mathrm {k}\Omega \)
• Berechnung von \(R_2\): \( \frac {R_\mathrm {F}}{R_2} = 0,8 \Rightarrow R_2 = \frac {R_\mathrm {F}}{0,8} = \frac {10\,\mathrm {k}\Omega }{0,8} = 12,5\,\mathrm {k}\Omega \)

3. Realisierung der Schaltung

Die verwendeten Widerstände: \begin {align*} R_\mathrm {F} &= 10\,\mathrm {k}\Omega \\ R_1 &= 2\,\mathrm {k}\Omega \\ R_2 &= 12,5\,\mathrm {k}\Omega \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

12 Entwurf einer Verstärkerschaltung mit unterschiedlichen Eingangsverstärkungen

Zwischen der Ausgangsspannung \(U_\mathrm {a}\) und dem Eingangsspannungen \(U_\mathrm {1}\) und \(U_\mathrm {2}\) besteht der folgende funktionale Zusammenhang: \(U_\mathrm {a} = 2 \ U_\mathrm {1} - 0,5 \ U_\mathrm {2}\) Geben Sie eine mit Operationsverstärker(n) und Widerständen aufgebaute Schaltung zur Realisierung dieses funktionalen Zusammenhangs an. Die Operationsverstärker dürfen als ideale Operationsverstärker angenommen werden. Geben Sie Werte der verwendeten Widerstände an! Typische Widerstände für OPV-Schaltungen liegen im Bereich von \(\mathrm {1\,k\Omega \ bis\ 100\,k\Omega }\).

12.1 Lösung:

Der funktionale Zusammenhang zwischen der Ausgangsspannung \( U_a \) und den Eingangsspannungen \( U_{e1} \) und \( U_{e2} \) lautet: \[ U_\mathrm {a} = 2 U_\mathrm {e1} - 0{,}5 U_\mathrm {e2} \]

1. Allgemeine Formel für die Ausgangsspannung eines Subtrahierers: \[ U_\mathrm {a} = U_\mathrm {e2} \cdot \frac {R_1 + R_3}{R_2 + R_4} \cdot \frac {R_4}{R_1} - U_\mathrm {e1} \cdot \frac {R_3}{R_1} \] Vergleich mit der Vorgabe \( U_\mathrm {a} = 2 U_\mathrm {e1} - 0{,}5 U_\mathrm {e2} \) ergibt folgende Bedingungen:

- Verstärkungsfaktor für \( U_\mathrm {e1} \): \( \frac {R_3}{R_1} = 0{,}5 \)

- Verstärkungsfaktor für \( U_\mathrm {e2} \): \( \frac {R_1 + R_3}{R_2 + R_4} \cdot \frac {R_4}{R_1} = 2 \)

2. Vorgehen:
- Setze \( R_3 = 1\,\mathrm {k}\Omega \) (typischer Wert).
- Berechne die restlichen Widerstände.

3. Berechnung der Widerstände:

Berechnung von \( R_1 \) (aus \( \frac {R_3}{R_1} = 0{,}5 \)): \[ \frac {R_3}{R_1} = 0{,}5 \Rightarrow R_1 = \frac {R_3}{0{,}5} = \frac {1\,\mathrm {k}\Omega }{0{,}5} = 2\,\mathrm {k}\Omega \]

Berechnung von \( R_2 \) und \( R_4 \) (aus \( \frac {R_1 + R_3}{R_2 + R_4} \cdot \frac {R_4}{R_1} = 2 \)): Setze \( R_4 = 1\,\mathrm {k}\Omega \): \[ \frac {R_1 + R_3}{R_2 + R_4} \cdot \frac {R_4}{R_1} = 2 \Rightarrow \frac {3\,\mathrm {k}\Omega }{R_2 + 1\,\mathrm {k}\Omega } \cdot \frac {1\,\mathrm {k}\Omega }{2\,\mathrm {k}\Omega } = 2 \] Multipliziere beide Seiten: \[ \frac {3}{2} = 2 \cdot (R_2 + 1\,\mathrm {k}\Omega ) \] Umstellen nach \( R_2 \): \[ R_2^2 + R_2 - \frac {3}{2} = 0 \]

4. Lösung mit der PQ-Formel:

Die quadratische Gleichung hat die Form: \[ R_2^2 + p \cdot R_2 + q = 0 \text {mit} p = 1, \, q = -\frac {3}{2} \] PQ-Formel: \[ R_2 = -\frac {p}{2} \pm \sqrt {\left ( \frac {p}{2} \right )^2 - q} \] Einsetzen der Werte: \[ R_2 = -\frac {1}{2} \pm \sqrt {\left ( \frac {1}{2} \right )^2 - \left ( -\frac {3}{2} \right )} = -\frac {1}{2} \pm \sqrt {\frac {1}{4} + \frac {3}{2}} \] \[ R_2 = -\frac {1}{2} \pm \sqrt {\frac {7}{4}} = -\frac {1}{2} \pm \frac {\sqrt {7}}{2} \] Da \( R_2 \) positiv sein muss: \[ R_2 = -\frac {1}{2} + \frac {\sqrt {7}}{2} \approx 1{,}82\,\mathrm {k}\Omega \]

5. Ergebnis der Widerstände: \begin {align*} R_1 &= 2\,\mathrm {k}\Omega \\ R_2 &= 1{,}82\,\mathrm {k}\Omega \\ R_3 &= 1\,\mathrm {k}\Omega \\ R_4 &= 1\,\mathrm {k}\Omega \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

13 Verstärkungseinstellung mit schaltbaren Widerständen

Um die Verstärkung eines OPVs einzustellen, können mithilfe von Schaltern verschiedene Widerstände am OPV zu- und abgeschaltet werden. Berechnen Sie die untenstehenden OP-Schaltungen in Abhängigkeit der Schalterstellungen S!

• Für die folgende Schaltung mit vier möglichen Schalterstellungen

• Für die folgende Schaltung mit zwei möglichen Schalterstellungen

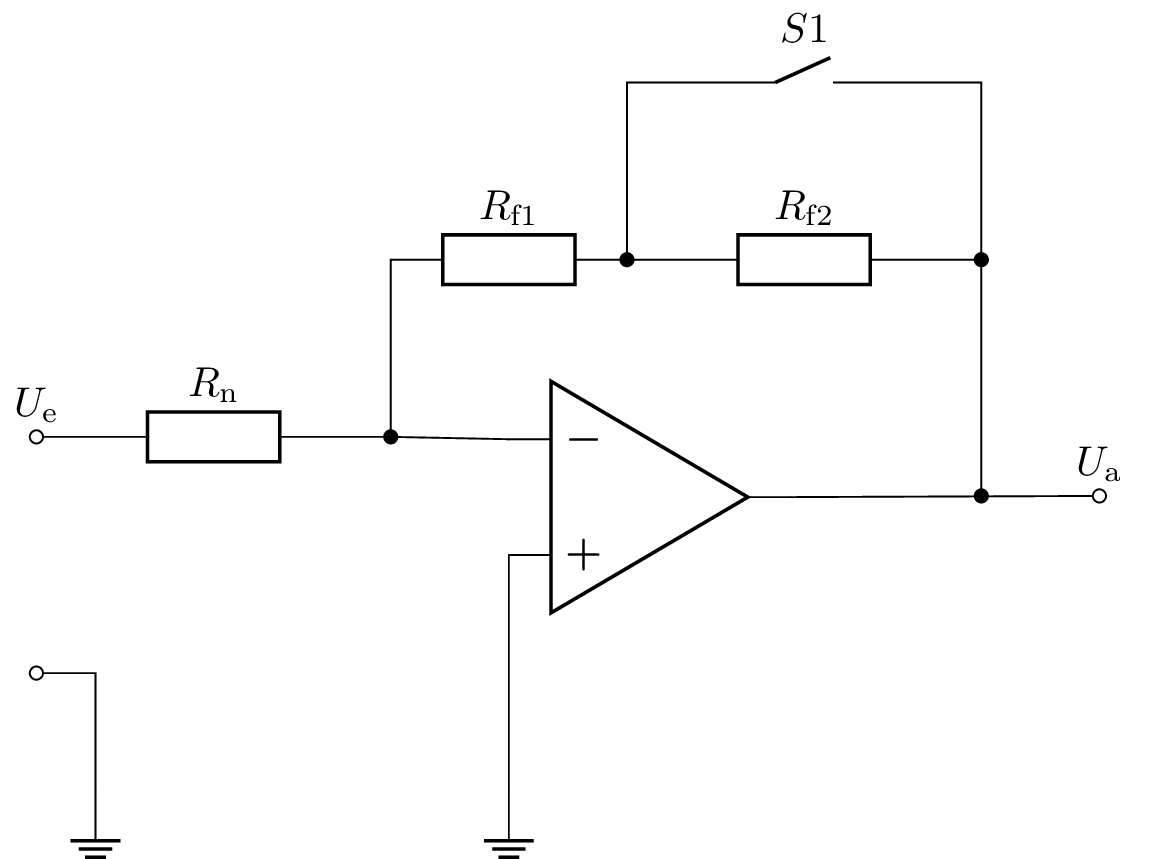
13.1 Lösung:

• Nicht-invertierender Verstärker

  1. Fall (S1 geschlossen, S2 offen): In diesem Zustand bilden die Widerstände \(R_\mathrm {n1}\) und \(R_\mathrm {n2}\) eine Serienschaltung. Die Gesamtverstärkung ergibt sich somit zu: \[ V = 1 + \frac {R_\mathrm {f}}{R_\mathrm {n1} + R_\mathrm {n2}} \]

  2. Fall (S1 offen, S2 geschlossen): In diesem Fall sind der Widerstand \(R_\mathrm {f}\) und \(R_\mathrm {n1}\) seriell geschaltet. Diese Serienschaltung bildet zusammen mit dem Widerstand \(R_\mathrm {n2}\) die Rückkopplungsschleife. Die Verstärkung ist daher: \[ V = 1 + \frac {R_\mathrm {f} + R_\mathrm {n1}}{R_\mathrm {n2}} \]

  3. Fall (S1 und S2 geschlossen): Mit beiden Schaltern geschlossen wird der Widerstand \(R_\mathrm {n1}\) überbrückt und somit nicht berücksichtigt. Die Verstärkung ergibt sich durch: \[ V = 1 + \frac {R_\mathrm {f}}{R_\mathrm {n2}} \]

  4. Fall (S1 und S2 offen): Wenn beide Schalter offen sind, fehlt der Rückkopplungspfad vollständig, womit die Verstärkung theoretisch unendlich groß ist: \[ V = \infty \]

• Invertierender Verstärker
  1. Zustand (S1 offen): Sind \(R_\mathrm {f1}\) und \(R_\mathrm {f2}\) seriell geschaltet, ergibt sich eine größere Rückkopplung und somit eine höhere Verstärkung. Die Verstärkung errechnet sich wie folgt: \[ V = -\frac {R_\mathrm {f1} + R_\mathrm {f2}}{R_\mathrm {n}} \]

  2. Zustand (S1 geschlossen, S2 offen): In diesem Zustand wird der Widerstand \(R_\mathrm {f2}\) durch den geschlossenen Schalter kurzgeschlossen und nicht berücksichtigt. Die Verstärkung reduziert sich damit auf: \[ V = -\frac {R_\mathrm {f1}}{R_\mathrm {n}} \]

Siehe: Abschnitt ?? und Tabelle ??

14 Berechnung der Ausgangsspannung mit mehreren Eingangsspannungen

Gegeben ist die abgebildete Schaltung mit einem idealen Operationsverstärker. Die Betriebsspannung beträgt \(\pm 15\,\mathrm {V}\).

• Die Widerstände sind alle gleich, es gilt \(R_1 = R_2 = R_3 = R_\mathrm {F} = \mathrm {1\,k\Omega }\). Die Spannung \(U_\mathrm {E1} = \mathrm {1\,V}\), \(U_\mathrm {E2} = \mathrm {2\,V}\), \(U_\mathrm {E3} = \mathrm {3\,V}\). Wie hoch ist die Spannung am Ausgang \(U_\mathrm {A}\)?
• Die Eingangsspannungen bleiben gleich groß, nur die Widerstände betragen nun \(R_\mathrm {F} = \mathrm {10\,k\Omega }, R_1=\mathrm {2\,k\Omega }, R_2=\mathrm {5\,k\Omega }, R_3=\mathrm {10\,k\Omega }\). Wie hoch ist die Spannung am Ausgang U\(_A\)?
• Die Eingangsspannungen bleiben gleich groß, nur die Widerstände betragen nun \(R_\mathrm {F} = \mathrm {10\,k\Omega }, R_1 = \mathrm {10\,k\Omega }, R_2 = \mathrm {5\,k\Omega }, R_3 = \mathrm {2\,k\Omega }\). Wie hoch ist die Spannung am Ausgang \(U_\mathrm {A}\)?

14.1 Lösung:

Gegeben ist eine Summierschaltung mit einem idealen Operationsverstärker und einer Betriebsspannung von \(\pm 15\,\mathrm {V}\).

Die allgemeine Formel für die Ausgangsspannung lautet: \[ U_\mathrm {A} = -\left ( U_\mathrm {E1} \cdot \frac {R_\mathrm {F}}{R_1} + U_\mathrm {E2} \cdot \frac {R_\mathrm {F}}{R_2} + U_\mathrm {E3} \cdot \frac {R_\mathrm {F}}{R_3} \right ) \]

a) Alle Widerstände sind gleich groß: \(R_1 = R_2 = R_3 = R_F = 10\,\mathrm {k}\Omega \)

Eingangsspannungen: \[ U_\mathrm {E1} = 1\,\mathrm {V}, U_\mathrm {E2} = 2\,\mathrm {V}, U_\mathrm {E3} = 3\,\mathrm {V} \]

Berechnung: \[ U_\mathrm {A} = -\left ( 1\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } + 2\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } + 3\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } \right ) \] \[ U_A = -\left ( 1\,\mathrm {V} + 2\,\mathrm {V} + 3\,\mathrm {V} \right ) = -6\,\mathrm {V} \]

b) Geänderte Widerstände: \(R_\mathrm {F} = 10\,\mathrm {k}\Omega \), \(R_1 = 2\,\mathrm {k}\Omega \), \(R_2 = 5\,\mathrm {k}\Omega \), \(R_3 = 10\,\mathrm {k}\Omega \)

Eingangsspannungen: \[ U_\mathrm {E1} = 1\,\mathrm {V}, U_\mathrm {E2} = 2\,\mathrm {V}, U_\mathrm {E3} = 3\,\mathrm {V} \]

Berechnung: \[ U_\mathrm {A} = -\left ( 1\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{2\,\mathrm {k}\Omega } + 2\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{5\,\mathrm {k}\Omega } + 3\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } \right ) \] \[ U_\mathrm {A} = -\left ( 1\,\mathrm {V} \cdot 5 + 2\,\mathrm {V} \cdot 2 + 3\,\mathrm {V} \cdot 1 \right ) \] \[ U_\mathrm {A} = -(5\,\mathrm {V} + 4\,\mathrm {V} + 3\,\mathrm {V}) = -12\,\mathrm {V} \]

c) Geänderte Widerstände: \(R_\mathrm {F} = 10\,\mathrm {k}\Omega \), \(R_1 = 10\,\mathrm {k}\Omega \), \(R_2 = 5\,\mathrm {k}\Omega \), \(R_3 = 2\,\mathrm {k}\Omega \)

Eingangsspannungen: \[ U_\mathrm {E1} = 1\,\mathrm {V}, U_\mathrm {E2} = 2\,\mathrm {V}, U_\mathrm {E3} = 3\,\mathrm {V} \]

Berechnung: \[ U_\mathrm {A} = -\left ( 1\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{10\,\mathrm {k}\Omega } + 2\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{5\,\mathrm {k}\Omega } + 3\,\mathrm {V} \cdot \frac {10\,\mathrm {k}\Omega }{2\,\mathrm {k}\Omega } \right ) \] \[ U_\mathrm {A} = -\left ( 1\,\mathrm {V} \cdot 1 + 2\,\mathrm {V} \cdot 2 + 3\,\mathrm {V} \cdot 5 \right ) \] \[ U_\mathrm {A} = -(1\,\mathrm {V} + 4\,\mathrm {V} + 15\,\mathrm {V}) = -20\,\mathrm {V} \]

Da die Betriebsspannung \(\pm 15\,\mathrm {V}\) beträgt, wird der Ausgang auf \(-15\,\mathrm {V}\) begrenzt.

Zusammenfassung:

• a) \(U_\mathrm {A} = -6\,\mathrm {V}\)
• b) \(U_\mathrm {A} = -12\,\mathrm {V}\)
• c) \(U_\mathrm {A} = -15\,\mathrm {V}\) (Begrenzung durch Betriebsspannung)

Siehe: Abschnitt ?? und Tabelle ??

15 Ausgangsspannung einer zweistufigen OPV-Schaltung bestimmen

Gegeben ist die folgende Schaltung. Berechnen Sie die Ausgangsspannung \( U_\mathrm {a} \).
Die Widerstandswerte lauten:
\( R_\mathrm {1} = \mathrm {10\,k\Omega }, \ R_\mathrm {2} = \mathrm {30\,k\Omega }, \ R_\mathrm {3} = \mathrm {30\,k\Omega }, \ R_\mathrm {4} = \mathrm {10\,k\Omega } \)

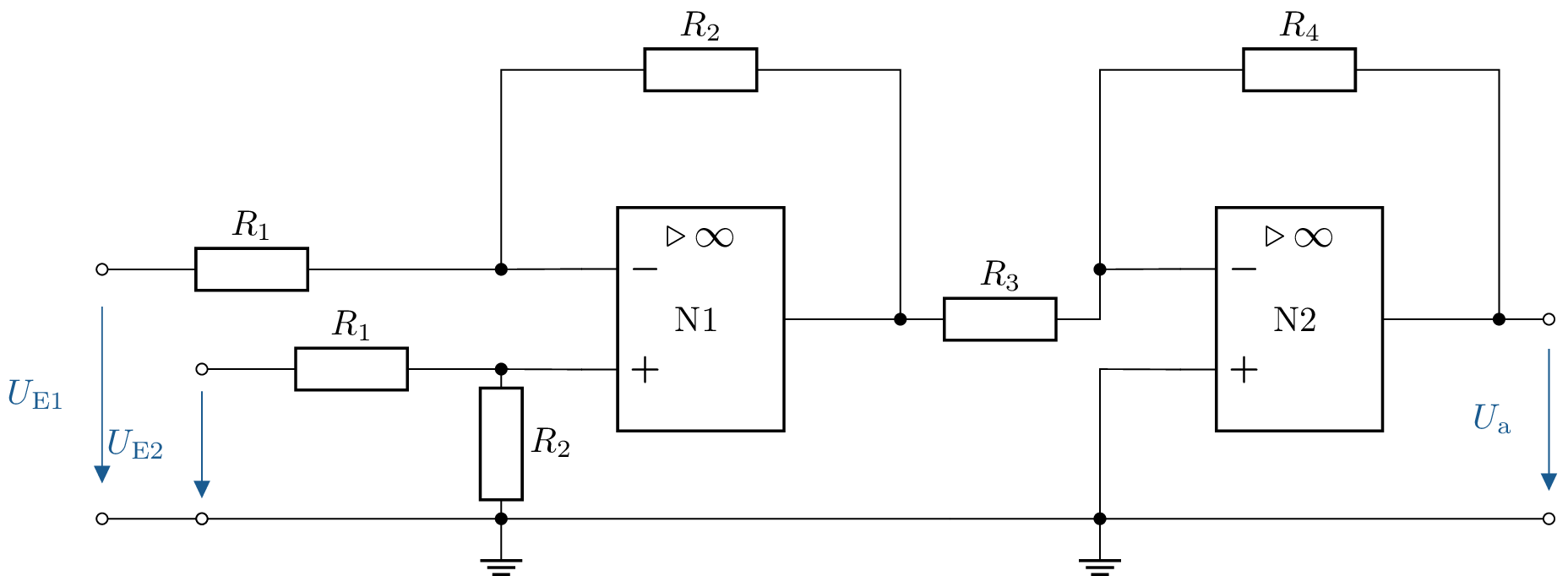
15.1 Lösung:

Die Ausgangsspannung nach dem ersten Operationsverstärker (\( U_\mathrm {a1} \)) ergibt sich zu: \begin {align*} U_\mathrm {a1} &= (U_\mathrm {E1} - U_\mathrm {E2}) \cdot \frac {R_\mathrm {2}}{R_\mathrm {1}} \\ U_\mathrm {a1} &= \frac {\mathrm {30\,k\Omega }}{\mathrm {10\,k\Omega }} \cdot (U_\mathrm {E1} - U_\mathrm {E2}) \end {align*}

Daraus ergibt sich für die gesamte Ausgangsspannung (\( U_\mathrm {a} \)): \begin {align*} U_\mathrm {a} &= - \frac {R_\mathrm {4}}{R_\mathrm {3}} \cdot U_\mathrm {a1} \\ U_\mathrm {a} &= - \frac {\mathrm {10\,k\Omega }}{\mathrm {30\,k\Omega }} \cdot \frac {\mathrm {30\,k\Omega }}{\mathrm {10\,k\Omega }} \cdot (U_\mathrm {E1} - U_\mathrm {E2}) \\ U_\mathrm {a} &= U_\mathrm {E2} - U_\mathrm {E1} \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

16 Berechnung einer OPV-Schaltung mit drei Eingängen

Gegeben ist die unten abgebildete Schaltung. Bestimmen Sie die Ausgangsspannung \( U_\mathrm {A} \).
Die Widerstandswerte lauten:
\( R_\mathrm {1} = \mathrm {10\,k\Omega },\ R_\mathrm {2} = \mathrm {20\,k\Omega },\ R_\mathrm {3} = \mathrm {30\,k\Omega },\ R_\mathrm {4} = \mathrm {10\,k\Omega },\ R_\mathrm {5} = \mathrm {20\,k\Omega },\ R_\mathrm {6} = \mathrm {40\,k\Omega } \)

16.1 Lösung:

Ausgangsspannung nach 1. OPV mit folgender Formel berechnen (\(U_{\mathrm {A1}}\)): \begin {align*} U_\mathrm {A1} &= - (U_\mathrm {E1} \cdot \frac {R_4}{R_1} + U_\mathrm {E2} \cdot \frac {R_4}{R_2} + U_\mathrm {E3} \cdot \frac {R_4}{R_3}) \\ U_\mathrm {A1}&= - (U_\mathrm {E1} \cdot \frac {10}{10} + U_\mathrm {E2} \cdot \frac {10}{20} + U_\mathrm {E3} \cdot \frac {10}{30}) \\ U_\mathrm {A1} &= - (U_\mathrm {E1} + \frac {1}{2} \cdot U_\mathrm {E2} + \frac {1}{3} \cdot U_\mathrm {E3}) \\ \end {align*}

Daraus egibt sich für die gesamte Ausgangsspannung (\(U_\mathrm {A}\)): \begin {align*} U_\mathrm {A} &= - \frac {R_6}{R_5} \cdot U_\mathrm {\mathrm {A1}} \\ U_\mathrm {A} &= - \frac {40}{20} \cdot (- (U_\mathrm {E1} + \frac {1}{2} \cdot U_\mathrm {E2} + \frac {1}{3} \cdot U_\mathrm {E3})) \\ U_\mathrm {A} &= 2 \cdot U_\mathrm {E1} + U_\mathrm {E2} + \frac {2}{3} \cdot U_\mathrm {E3} \end {align*}

Siehe: Abschnitt ?? und Tabelle ??

17 Untersuchung der Verstärkung eines OPVs mit variablen Widerständen

Untersuchen Sie die Verstärkung eines nicht-invertierenden Operationsverstärkers mit variablen Widerständen und berechnen Sie die Ausgangsspannung \(U_\mathrm {A}\).

Gegeben:

• Versorgungsspannung: \(\pm 15\,\mathrm {V}\)
• Eingangsspannung: \(U_\mathrm {E} = 1\,\mathrm {V}\)
• Rückkopplungswiderstand: \(R_\mathrm {R} = 100\,\Omega \)
• Eingangswiderstand: \(R_\mathrm {E} = 680\,\Omega \)
• Weitere mögliche Widerstandswerte: \(R_\mathrm {R} = 220\,\Omega \), \(R_\mathrm {E} = 680\,\Omega \)
• Lastwiderstand: \(R_\mathrm {Last} = 10\,\mathrm {k\Omega }\)

• Berechnen Sie die Verstärkung \(V\) und die Ausgangsspannung \(U_\mathrm {A}\) für die gegebenen Widerstandswerte.
• Wie ändert sich die Verstärkung, wenn \(R_\mathrm {R}\) von \(100\,\Omega \) auf \(220\,\Omega \) erhöht wird?
• Welche Auswirkungen hat eine Änderung von \(R_\mathrm {E}\) auf die Verstärkung und die Ausgangsspannung?
• Welche Begrenzungen für \(U_\mathrm {A}\) ergeben sich durch die Versorgungsspannung?

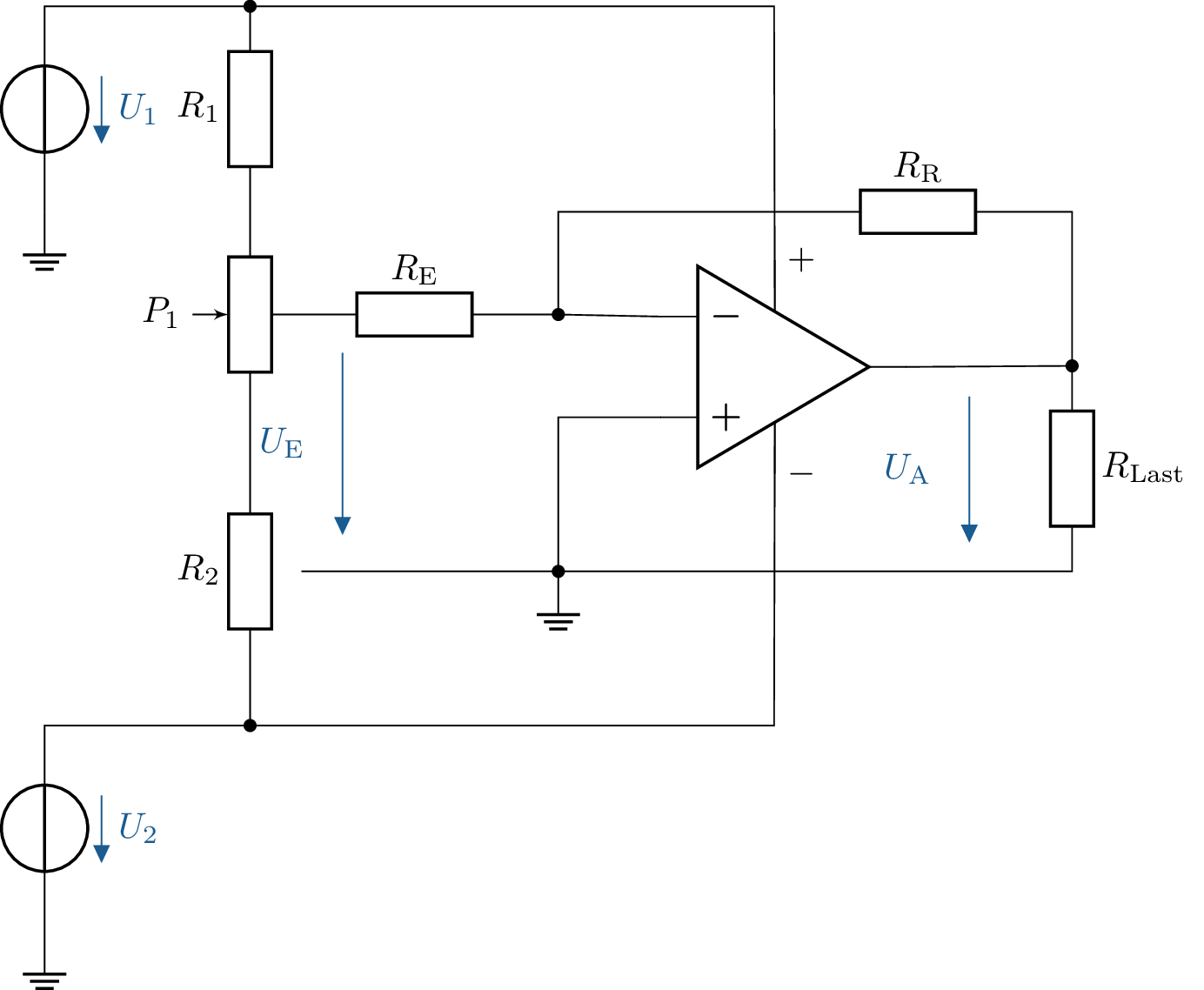
17.1 Lösung:

a) Berechnung der Ausgangsspannung \(U_\mathrm {A}\)
Gegeben sind: \[ U_\mathrm {E} = 1\,\mathrm {V}, R_\mathrm {R} = 100\,\Omega , R_\mathrm {E} = 680\,\Omega \] Einsetzen in die Verstärkungsformel: \[ V = 1 + \frac {R_\mathrm {R}}{R_\mathrm {E}} \] \[ V = 1 + \frac {100\,\Omega }{680\,\Omega } = 1 + 0{,}147 = 1{,}147 \] Die Ausgangsspannung berechnet sich zu: \[ U_\mathrm {A} = V \cdot U_\mathrm {E} = 1{,}147 \cdot 1\,\mathrm {V} = 1{,}147\,\mathrm {V} \]

b) Änderung von \(R_\mathrm {R}\) auf \(220\,\Omega \)
Wenn \(R_\mathrm {R} = 220\,\Omega \) gewählt wird: \[ V = 1 + \frac {220\,\Omega }{680\,\Omega } = 1 + 0{,}323 = 1{,}323 \] \[ U_\mathrm {A} = 1{,}323 \cdot 1\,\mathrm {V} = 1{,}323\,\mathrm {V} \]

c) Einfluss von \(R_\mathrm {E}\) auf die Verstärkung
Eine Vergrößerung von \(R_\mathrm {E}\) führt zu einer kleineren Verstärkung \(V\), während eine Verkleinerung von \(R_\mathrm {E}\) die Verstärkung erhöht. In der Praxis sollte \(R_\mathrm {E}\) so gewählt werden, dass das Ausgangssignal nicht zu stark schwankt.

d) Begrenzung von \(U_\mathrm {A}\) durch die Versorgungsspannung
Die Ausgangsspannung \(U_\mathrm {A}\) kann niemals über die Versorgungsspannung \(\pm 15\,\mathrm {V}\) hinausgehen. Falls \(U_\mathrm {A}\) rechnerisch diesen Bereich überschreiten würde, wird die Ausgangsspannung auf maximal \(15\,\mathrm {V}\) begrenzt. Siehe: Abschnitt ?? und Tabelle ??

18 Analyse eines nicht-invertierenden Verstärkers mit Last

Analysieren Sie die Verstärkung eines nicht-invertierenden Operationsverstärkers und berechnen Sie die Ausgangsspannung \(U_\mathrm {A}\). Gegeben:

• Versorgungsspannung: \(\pm 15\,\mathrm {V}\)
• Eingangsspannung: \(U_\mathrm {E} = 1\,\mathrm {V}\)
• Rückkopplungswiderstand: \(R_\mathrm {R} = 20\,\mathrm {k\Omega }\)
• Eingangswiderstand: \(R_\mathrm {E} = 10\,\mathrm {k\Omega }\)
• Lastwiderstand: \(R_\mathrm {Last} = 10\,\mathrm {k\Omega }\)

• Berechnen Sie die Ausgangsspannung \(U_\mathrm {A}\) mit den gegebenen Werten.
• Wie verändert sich \(U_\mathrm {A}\), wenn \(R_\mathrm {R}\) auf \(30\,\mathrm {k\Omega }\) erhöht wird?
• Welchen Einfluss hat der Lastwiderstand \(R_\mathrm {Last}\) auf das Ausgangssignal?

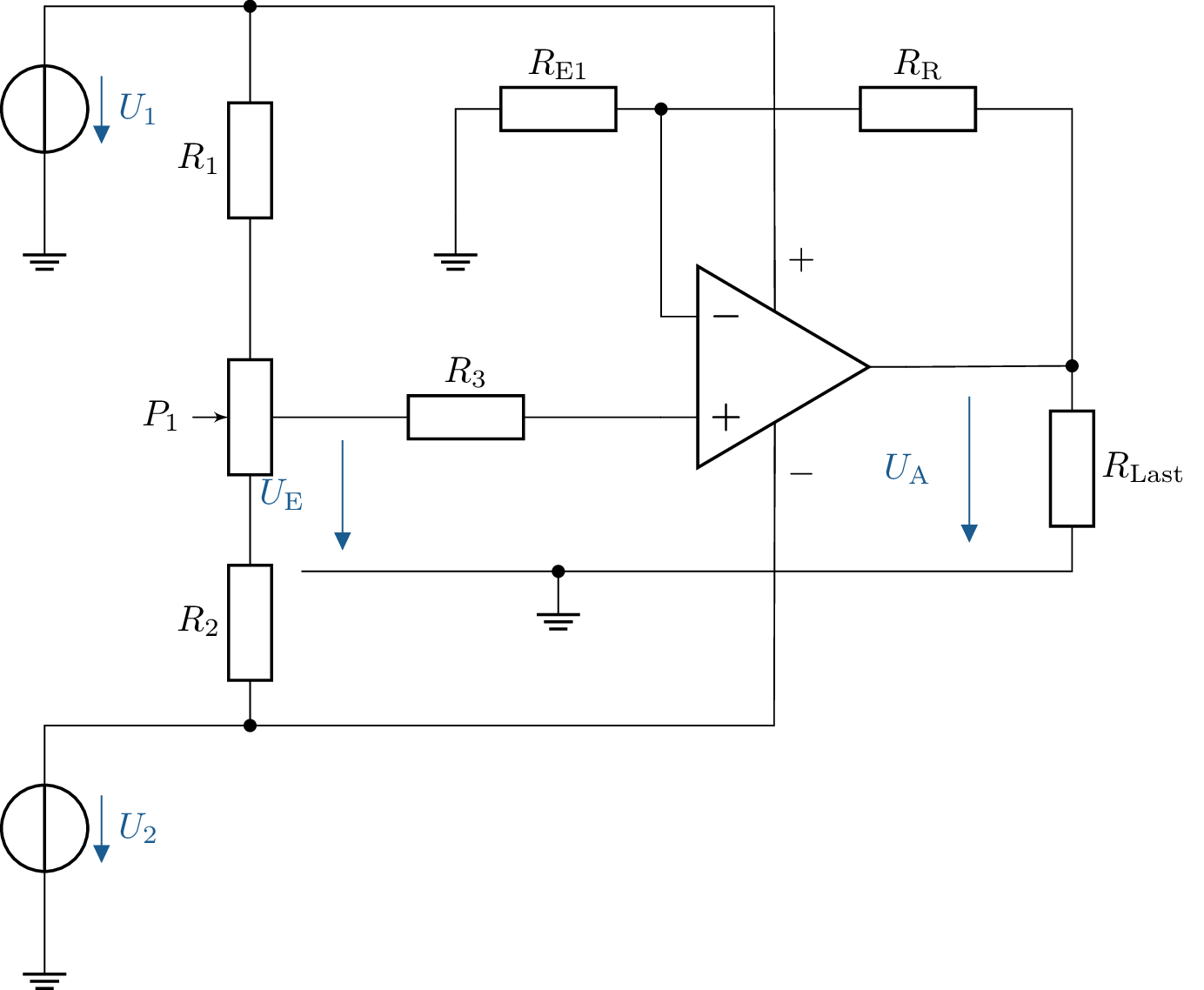
18.1 Lösung:

a) Berechnung der Ausgangsspannung \(\mathrm {U_A}\)
Gegeben sind: \[ U_\mathrm {E} = 1\,\mathrm {V}, R_\mathrm {R} = 20\,\mathrm {k\Omega }, R_\mathrm {E} = 10\,\mathrm {k\Omega } \] Einsetzen in die Verstärkungsformel: \[ V = 1 + \frac {R_\mathrm {R}}{R_\mathrm {E}} \] \[ V = 1 + \frac {20\,\mathrm {k\Omega }}{10\,\mathrm {k\Omega }} = 1 + 2 = 3 \] Die Ausgangsspannung ergibt sich zu: \[ U_\mathrm {A} = V \cdot U_\mathrm {E} = 3 \cdot 1\,\mathrm {V} = 3\,\mathrm {V} \]

b) Veränderung von \(\mathrm {R_R}\)
Wenn \(R_\mathrm {R}\) auf \(30\,\mathrm {k\Omega }\) erhöht wird: \[ V = 1 + \frac {30\,\mathrm {k\Omega }}{10\,\mathrm {k\Omega }} = 1 + 3 = 4 \] \[ U_\mathrm {A} = 4 \cdot 1\,\mathrm {V} = 4\,\mathrm {V} \]

c) Einfluss des Lastwiderstands
Der Lastwiderstand \(R_\mathrm {Last}\) beeinflusst die Schaltung nur minimal, solange der Operationsverstärker im linearen Bereich arbeitet. Falls der Lastwiderstand jedoch zu klein gewählt wird, kann der Operationsverstärker an seine Ausgangsstromgrenze kommen, was zu einer Spannungsbegrenzung führt.

Siehe: Abschnitt ?? und Tabelle ??

19 Spannungsteiler mit Operationsverstärker als Spannungsfolger

Zeichnen Sie einen neuen Schaltplan bestehend aus einem belasteten Spannungsteiler, der durch einen Operationsverstärker als Impedanzwandler ergänzt wird. Die Bauteilwerte sind wie folgt gegeben:

• Widerstände: \(R_1 = R_2 = 10\,\mathrm {k\Omega }\)
• Lastwiderstand: \(R_\mathrm {L} = 2{,}2\,\mathrm {k\Omega }\)
• Versorgungsspannung: \(\mathrm {U_{CC} = +15\,V}\)

Der Operationsverstärker wird als Impedanzwandler (Spannungsfolger) geschaltet. Sein Ausgang speist den Lastwiderstand \(R_\mathrm {L}\).

• Berechnen Sie die Ausgangsspannung \(U_\mathrm {C}\) mit und ohne Lastwiderstand \(\mathrm {R_L}\).
• Vergleichen Sie die Ergebnisse mit denen aus Aufgabe 13.
• Erklären Sie, warum sich die Spannung \(U_\mathrm {C}\) durch den Lastwiderstand in dieser Schaltung nicht ändert.

19.1 Lösung:

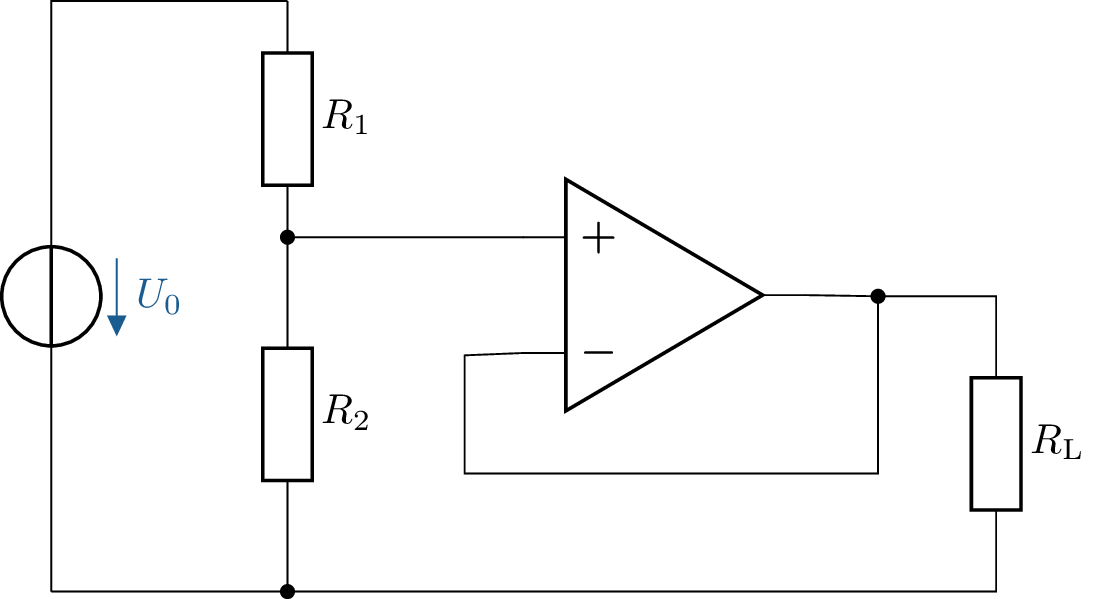
• Berechnung der Ausgangsspannung \(U_\mathrm {C}\) mit und ohne Lastwiderstand
  Da der Operationsverstärker als Spannungsfolger (Impedanzwandler) geschaltet ist, entspricht die Ausgangsspannung \(U_\mathrm {A}\) exakt der Spannung am Spannungsteiler: \[ U_\mathrm {A} = U_\mathrm {C} = 7{,}5\,\mathrm {V} \] Da der Operationsverstärker einen sehr hohen Eingangswiderstand hat, wird die Spannung nicht durch den Lastwiderstand beeinflusst. Somit bleibt die Ausgangsspannung konstant bei 7,5 V, unabhängig davon, ob \(R_\mathrm {L}\) angeschlossen ist oder nicht.
• Vergleich mit Aufgabe 13
  Im Gegensatz zur ersten Schaltung sinkt die Spannung hier nicht ab, wenn der Lastwiderstand \(R_\mathrm {L}\) angeschlossen wird. Der Operationsverstärker entkoppelt den Spannungsteiler von der Last, sodass der Spannungsteiler immer seine ursprüngliche Spannung hält.
• Erklärung der Spannungsstabilität durch den Operationsverstärker
  Der Operationsverstärker als Impedanzwandler besitzt einen hohen Eingangswiderstand und einen geringen Ausgangswiderstand. Dadurch wird der Lastwiderstand nicht mehr direkt mit dem Spannungsteiler verbunden, sondern erhält seinen Strom aus dem OPV. Dies führt dazu, dass die Ausgangsspannung stabil bleibt, unabhängig von der Belastung.

Siehe: Abschnitt ?? und Tabelle ??