Drehstrom

Um einen möglichst effizienten Energietransport zu gewährleisten wird in vielen Netzsystemen Drehstrom eingesetzt. Grundlage des Drehstrom ist der Wechselstrom, welcher nicht als einzelne Phase, sondern als Zusammenschluss von mehreren Phasen genommen wird. Erzeugt wird Wechselstrom mit Generatoren, die nicht nur eine einzelne Wicklung im Rotor verbaut haben, sondern mehrere. Werden diese Wicklungen mit einem symmetrischen Abstand zu einander verbaut, werden je nach Anzahl der Wicklungen Phasen erzeugt. Es wird dann von einem Mehrphasensysteme gesprochen. Wenn genau drei Phasen vorliegen, wird das System Drehstrom genannt. Für das Verständniss von Drehstrom sind besonders die Grundlagen zum Wechselstrom und dem komplexen Rechnen relevant.

1 Symmetrische Komponenten

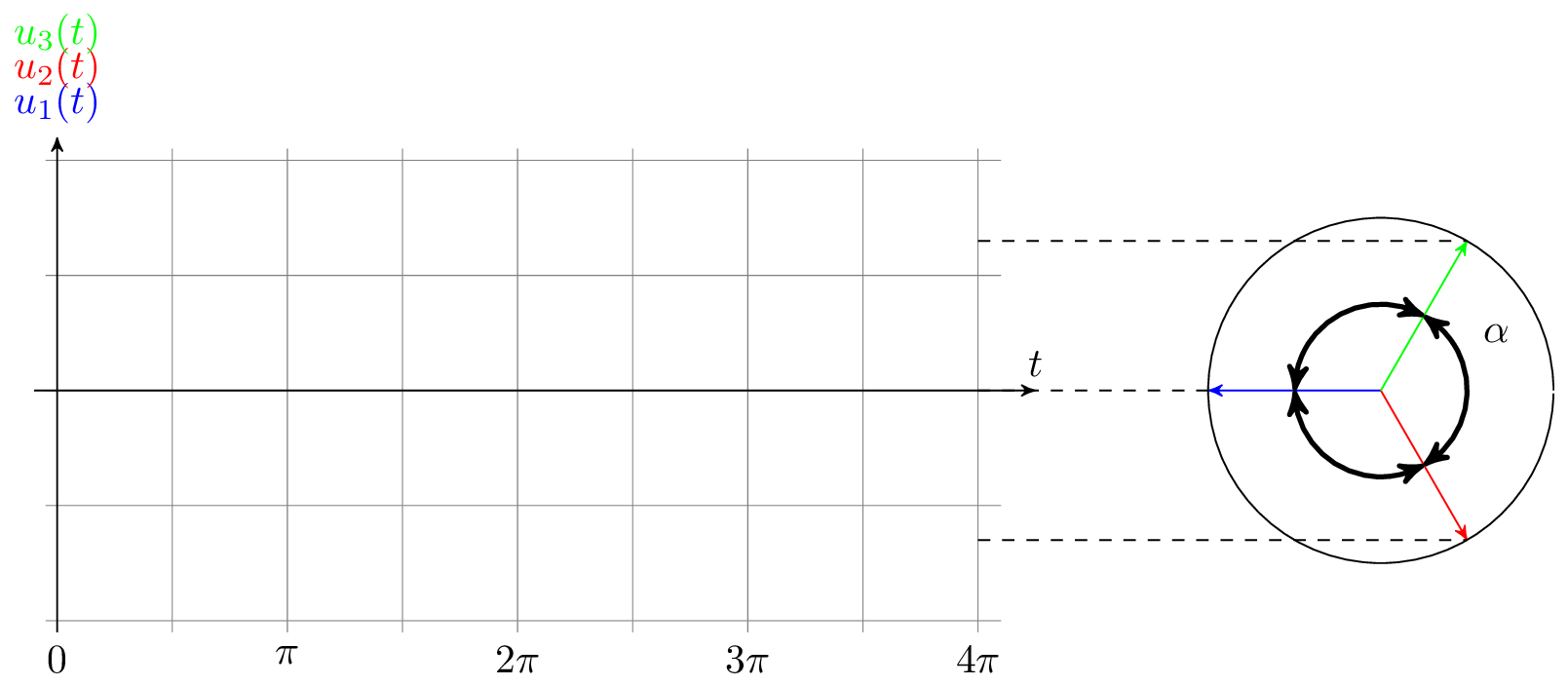
Im Bereich der Energieerzeugung, -übertragung und -verteilung wird hautpsächlich mit Drehstrom gearbeitet. Der Begriff „Drehstrom“kommt aus der technischen Gegebenheit, dass die Systeme mit dem räumlich rotierenden Magnetfeld des Generators verbunden sind: Dem Drehfeld. Alle Phasen in einem Mehrphasensystem werden mit der gleichen Frequenz erzeugt, die bekanntermaßen in Europa bei 50 Hz liegt. Die erzeugten Phasen werden am Ort der Erzeugung, also dem Generator, und hinter den Verbrauchern verschaltet. Im Drehstromsystem, also einem Drei-Phasen-System, stehen dafür die Sternschaltung oder die Dreiecksschaltung zur Verfügung. Im symmetrischen Fall erzeugt der Generator so viele Phasen, wie Wicklungen im Rotor verbaut sind. Die Wicklungen sind dabei mit immer im gleichen Winkel verbaut. Dieser Winkel bekommt den griechischen Buchstaben \(\alpha \) zugeordnet:

\begin {align} \alpha = \frac {2\pi }{m} \end {align}

Das m steht in der Formel für die Anzahl an Phasen, die in dem System erzeugt werden. Bei einem Drehstromsystem sind drei Phasen vorhanden. Daraus ergibt sich ein \(\alpha \) von 120°.

Im nächsten Schritt soll ein Drehoperator aus dem Winkel \(\alpha \) abgeleitet werden. Dieser Drehoperator dient der Umrechnung der Spannungen und Ströme zur Bezugsspannung/zum Bezugsstrom.

\begin {align} \underline {a}=e^{j\alpha }=e^{j\frac {2\pi }{m}} \label {Drehoperator} \end {align}

Für \(m=3\):

\begin {align} \underline {a}&=e^{j\frac {2\pi }{3}}=-\frac {1}{2}+j\frac {\sqrt {3}}{2} \notag \\ \underline {a}^2&=e^{j\frac {4\pi }{3}}=-\frac {1}{2}-j\frac {\sqrt {3}}{2}=\underline {a}^{*} \notag \\ \underline {a}^3&=e^{j2\pi }=1 \notag \\ \underline {a}^4&=e^{j\frac {8\pi }{3}}=-\frac {1}{2}+j\frac {\sqrt {3}}{2}=\underline {a} \notag \\ \underline {a}^5&=e^{j\frac {10\pi }{3}}=-\frac {1}{2}-j\frac {\sqrt {3}}{2}=\underline {a}^2 \notag \\ \vdots \notag \end {align}

Die komplexen Spannungen der jeweiligen Außenleiter gegenüber einem Neutralleiter können mit der folgenden Gleichung formuliert werden:

\begin {align} \underline {U}_{\mathrm {Lm}}=U_\mathrm {L1}\cdot e^{-j(m-1)\alpha } \end {align}

Die Spannung \(U_1\) ist dabei eine reele Bezugsgröße für das Mehrphasensystem.

Nun werden die Gleichungen für den Drehoperator mit der für die Spannung zusammengebracht und ergeben folgenden Zusammenhang:

\begin {align} \underline {U}_\mathrm {L1}&=\underline {a}^m\cdot U_\mathrm {L1}=1\cdot U_\mathrm {L1} \notag \\ \underline {U}_\mathrm {L2}&=\underline {a}^{m-1}\cdot U_\mathrm {L1} \notag \\ \vdots \notag \\ \underline {U}_{\mathrm {Lm-1}}&=\underline {a}^2\cdot U_\mathrm {L1} \notag \\ \underline {U}_{\mathrm {Lm}}&=\underline {a}\cdot U_\mathrm {L1} \notag \end {align}

Mit einer Anzahl von drei Phasen, also \(m=3\), ergibt sich folgender Zusammenhang der drei Spannungen und dem Drehoperator:

\begin {align} \underline {U}_\mathrm {L1}+\underline {U}_\mathrm {L2}+\underline {U}_\mathrm {L3}=U_1(1+\underline {a}^2+\underline {a}) \end {align}

Anmerkung:

In der Literatur sind die Indizes für die Spannungen nicht immer einheitlich gewählt. Die häufigste Alternative sind die Buchshtaben \(u, v ,w\) für die Phasen \(1, 2, 3\). Es werden noch weitere Indizes verwendet, die hier jedoch nicht weiter erwähnt werden sollen.

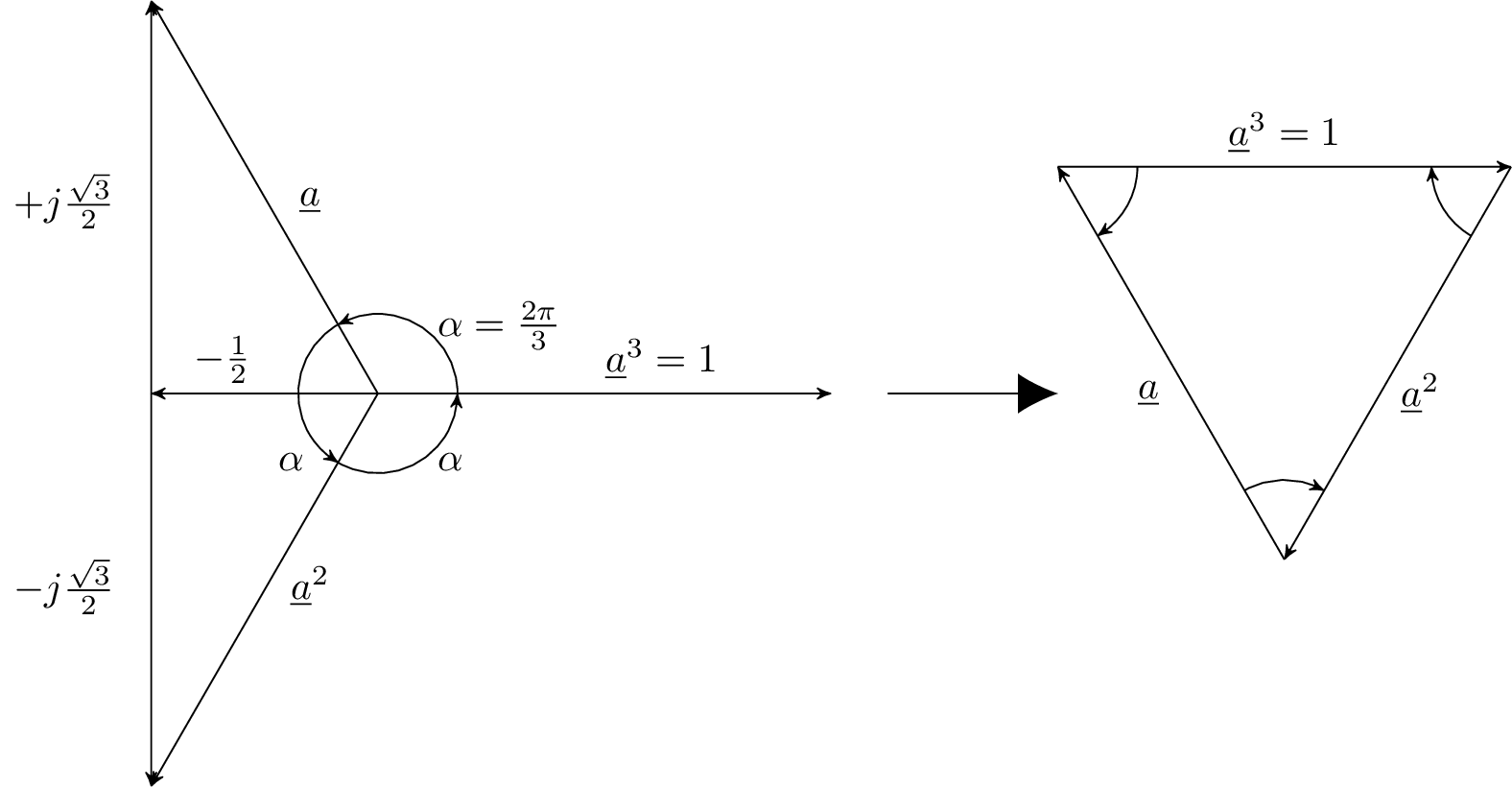
In Abb. 2 soll nochmals deutlich gemacht werden, wie sich die Drehoperatoren im Komplexen zusammensetzen.

Wird dem Weg über die drei Drehoperatoren gefolgt, gelangt man zurück zum Ursprung und erhält Null.

\begin {align} 1+\underline {a}+\underline {a}^2=0 \notag \\ \underline {U}_\mathrm {L1}+\underline {U}_\mathrm {L2}+\underline {U}_\mathrm {L3}=0 \notag \end {align}

1.1 Verkettete Systeme im Stern

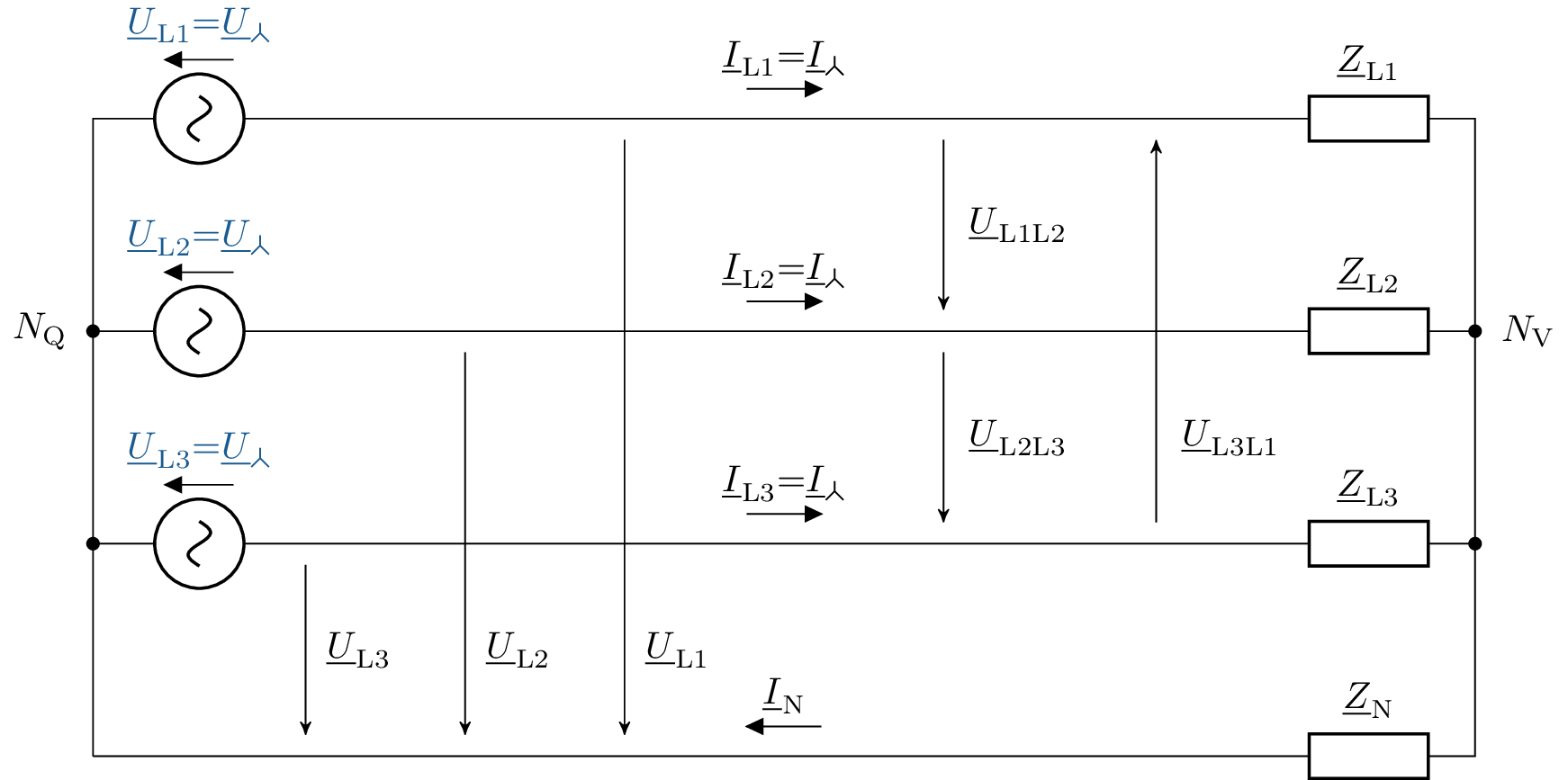
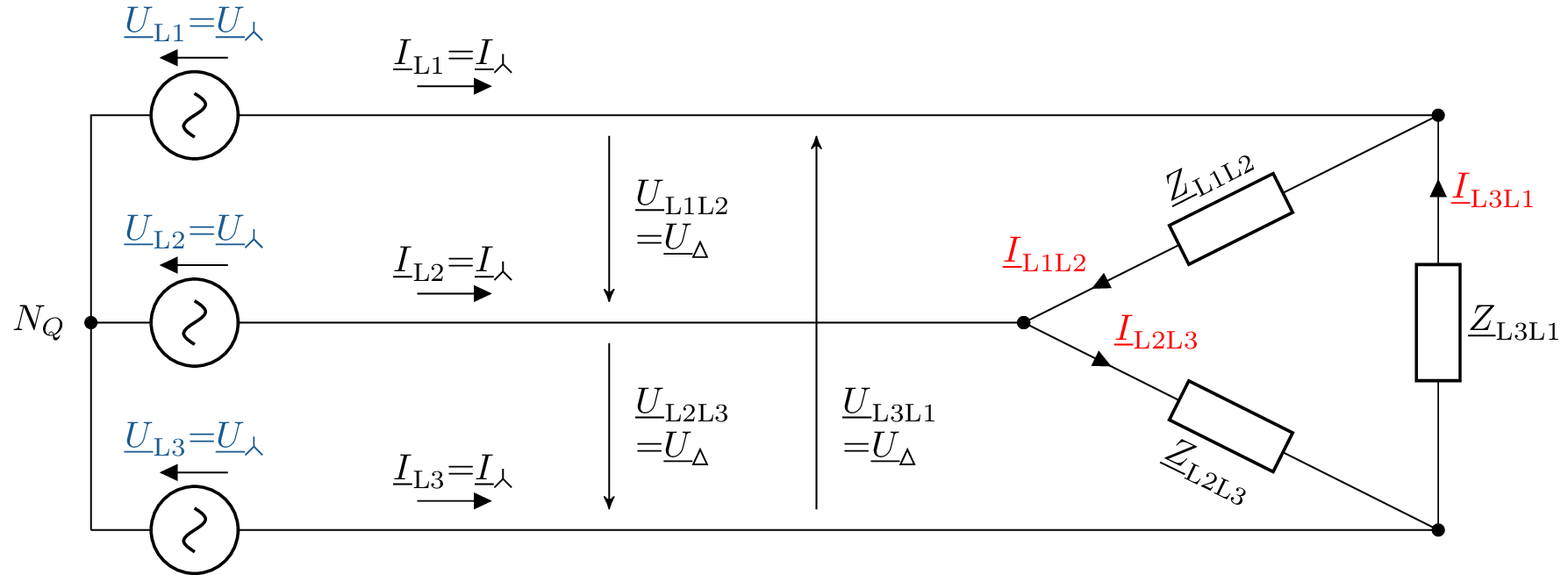
In den folgenden Kapiteln soll darauf eingegangen werden, welche Formen der Verschaltung in einem Drehstromsystem vorkommen können. Zuerst soll auf die sogenannte Sternschaltung eingegangen werden. Sternschaltung bedeutet, dass die Stränge so zusammengeführt werden, dass sich ein sogenannter Sternpunkt bildet. Ein System kann sowohl auf Generator-, als auch auf Verbraucherseite verschaltet werden. In Abb. 3 sind die die typischen Komponenten einer Sternschaltung in einem dreiphasigen Ersatzschaltbild eingetragen. Für jede Phase, die der Generator erzeugt wird eine Spannungsquelle eingetragen. Wenn der Generator eine Sternschaltung aufweist, werden in dem ESB auf die einzelnen Spannung in einem Knotenpunkt zusammengeführt. Dieser Knotenpunkt soll den Buchstaben \(N_Q\) erhalten. Von jeder Spannungsquelle geht ein Strang aus, welcher die jeweilige Phase wiederspiegeln soll. Auf Grund der physikalischen Gegebenheiten weisen die Komponenten, die nach dem Generator angeschlossen sind, also vor allem die Leitung und der Verbraucher, sowohl Wirk- wie auch Blindwiderstände auf. Diese werden in dem ESB zu jeweils einer Impedanz pro Strang zusammengefasst. Die Impedanzen der Stränge werden in der Sternschaltung wie auch die Spannungsquellen zu dem Knotenpunkt \(N_V\) zusammengeführt. In einem System, in dem sowohl die Generator- als auch die Verbraucherseite im Stern verschaltet sind, kann es zu den Strängen der Phasen noch einen Neutralleiter oder Rückleiter geben, welcher die beiden Knotenpunkte miteinander verbindet.

Spannungen

Grundsätzlich gibt es in einem Drehstromsystem drei Spannungen, welche spezifisch genannt werden sollten:

• Außenleiter-Neutralleiter-Spannung (Sternspannung) \(U_\Stern \): Spannung des Leiters gegenüber dem Neutralleiter (\(U_{\mathrm {L1}}\), \(U_{\mathrm {L2}}\), \(U_{\mathrm {L3}}\))
• Außenleiter-Spannung (verkettete Spannung) U: Spannung zwischen zwei Leitern (\(U_{\mathrm {L1L2}}\), \(U_{\mathrm {L2L3}}\), \(U_{\mathrm {L3L1}}\)) – diese Spannung wird auch als Dreieckspannung bezeichnet
• Strangspannung \(U_{\mathrm {str}}\): Spannung über die Impedanz des Leiters gegenüber dem Neutralleiter. Je nach Verschaltung ist die Strangspannung entweder gleich der Sternspannung oder der Dreieckspannung

Ströme

Für Ströme in einem Sternsystem ist es hilfreich das 1. Kirchhoffsche Gesetz anzuwenden. Die Summe der Ströme der Stränge muss gleich dem Strom im Neutralleiter sein:

\begin {align} \underline {I}_{\mathrm {N}}=\underline {I}_{\mathrm {L1}}+\underline {I}_{\mathrm {L2}}+\underline {I}_{\mathrm {L3}} \end {align}

Im Bezug zu den Spannungen und Impedanz ergibt sich nach dem Ohmschen Gesetz:

\begin {align} \underline {I}_{\mathrm {N}}=\frac {\underline {U}_{\mathrm {L1}}}{\underline {Z}_1}+\frac {\underline {U}_{\mathrm {L2}}}{\underline {Z}_2}+\frac {\underline {U}_{\mathrm {L3}}}{\underline {Z}_3}=\underline {U}_{\mathrm {1m}}\underline {Y}_{1}+\underline {U}_{\mathrm {2m}}\underline {Y}_{2}+\underline {U}_{\mathrm {3m}}\underline {Y}_{3} \end {align}

Wenn von einem symmetrischen System gesprochen wird, gilt das nicht nur für den Generator, sondern auch für die Impedanzen. Demnach sind die Impedanzen der drei Stränge alle gleich groß:

\begin {align} \underline {Z}_{\mathrm {L1}}=\underline {Z}_{\mathrm {L2}}=\underline {Z}_{\mathrm {L3}}=\underline {Z} \label {SymImpedanzen} \end {align}

Wird dieser Zusammenhang für ein symmetrisches System für die Gleichung ?? berücksichtigt, kann die Impedanz herausgezogen werden. Nun ist bereits bekannt, dass die Summe der Spannungen in einem symmetrischen System null ergibt. Somit lässt sich beweisen, dass die Summe der Ströme auch null ergeben muss.

\begin {align} \underline {I}_{\mathrm {N}}=\frac {1}{\underline {Z}}(\underline {U}_{\mathrm {L1}}+\underline {U}_{\mathrm {L2}}+\underline {U}_{\mathrm {L3}})=0 \end {align}

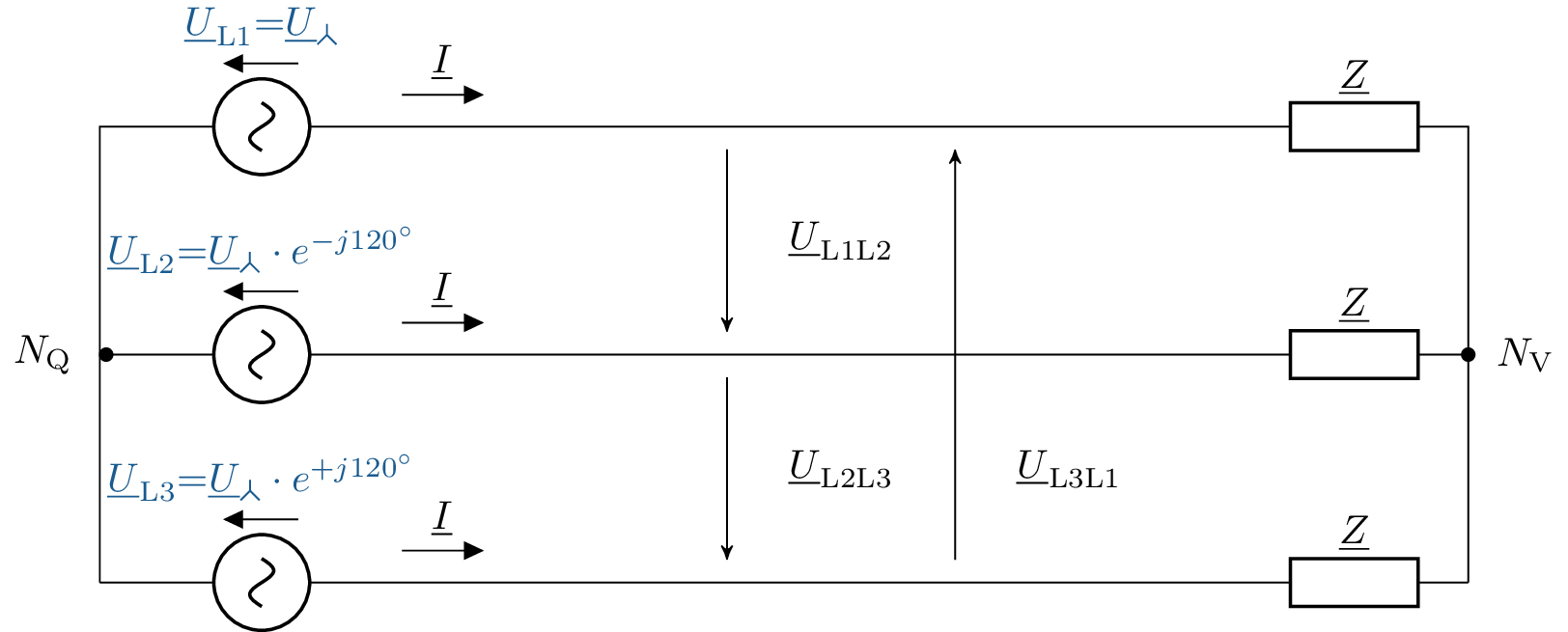
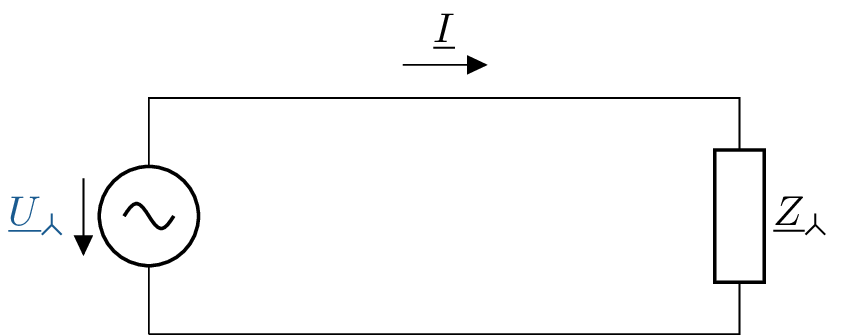
Um nicht immer das vollständige dreiphasige ESB zeichnen zu müssen, wie in Abb 4, gibt es die Möglichkeit, ein vereinfachtest einphasiges ESB zu zeichnen. Wichtig bei der Aufstellung des einphasigen ESB (natürlich auch bei jedem anderen ESB) ist, dass die korrekten Bezeichnungen für die Ströme, Spannungen und Impedanzen über die Indizes gewählt wird. Für die Sternschaltung ist das einphasige ESB in Abb. 5 abgebildet.

1.2 Verkettete Systeme im Dreieck

Alternativ zu der Verschaltung im Stern können die Quellen und Verbraucher im Dreieck verschaltet werden. Für die Generatorseite gilt jedoch, dass diese in den meisten Fällen im Stern verschaltet ist. Hintergrund ist, dass bei kleinsten unsymmetrien Ausgleichströme fließen, die den Betrieb des Generators beienflussen würden. Das soll möglichst vermieden werden, wodurch eine Sternschaltung eine bessere Betriebsweise darstellt. Deswegen wird angenommen, dass die Generatorseite grundlegend im Stern verschaltet ist. Wenn also von einer Dreieckschaltung die Rede ist, wird, außer es wird explizit erwähnt, nur die Verbraucherseite gemeint.

Es wurde bereits definiert, dass die Außenleiter-Spannung auch Dreiecksspannung genannt wird. Nach dem Maschen-Gesetz ergibt sich die Dreieckspannung zweier Leiter aus der Differenz der jeweiligen Sternspannung:

\begin {align} \underline {U}_{\mathrm {L1L2}}=\underline {U}_{\mathrm {L1}}-\underline {U}_{\mathrm {L2}} \label {AußenleiterKomplex} \end {align}

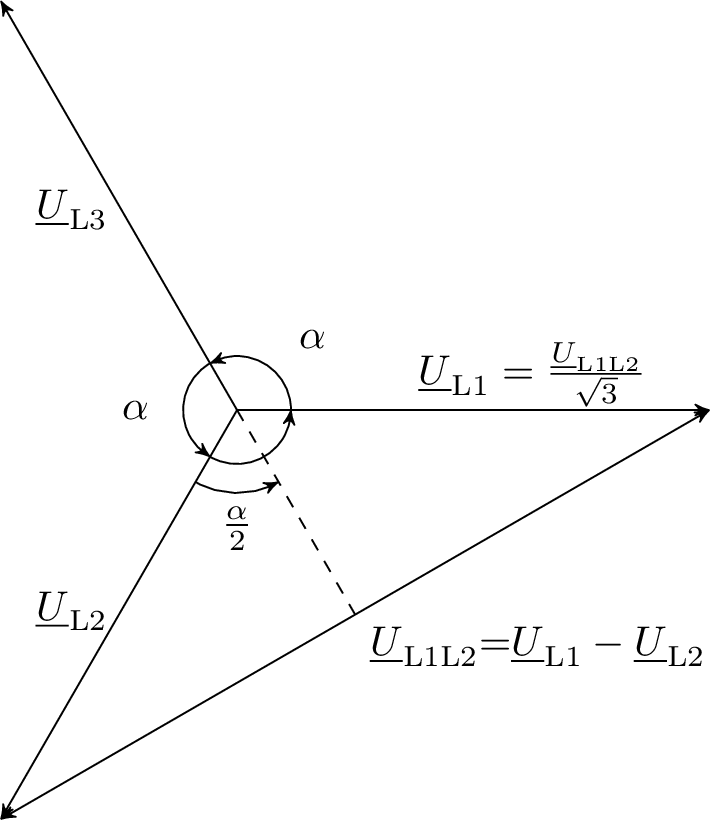
Wenn nun der Wert der jeweiligen Außenleiterspannung errechnet werden soll, müsste nach der Gleichung ?? komplex gerechnet werden. Es kann jedoch mit Hilfe einer trigonometrischen Herleitung ein Verhältnis zwischen Sternspannung und Dreiecksspannung beschrieben werden.

\begin {equation} \sin \left (\frac {\alpha }{2}\right )=\sin \left (\frac {\frac {2\pi }{m}}{2}\right )=\sin \left (\frac {\pi }{m}\right )=\frac {G}{H} \label {GleichungW3} \end {equation}

\begin {align} \sin \left (\frac {\pi }{3}\right )=\frac {\frac {\underline {U}_{\mathrm {L1L2}}}{2}}{\underline {U}_{\mathrm {L1}}} \notag \end {align} \begin {equation} 2\cdot \frac {\sqrt {3}}{2}=\frac {\underline {U}_{\mathrm {L1L2}}}{\underline {U}_{\mathrm {L1}}} \label {GleichungW32} \end {equation} \begin {align} \underline {U}_{\mathrm {L1}}=\frac {\underline {U}_{\mathrm {L1L2}}}{\sqrt {3}} \notag \end {align}

In Abb. 6 soll mit Hilfe des Zeigerdiagramm der komplexen Drehspannungen das Verhältinis zwischen Stern- und Dreieckspannung aufgezeigt werden. Dafür werden die trigonometrischen Grundlagen genommen, um die Länge der Außenleiterspannung (also der Dreieckspannung) anders darzustellen. In Gleichung 1 ist zuerst allgemein beschrieben, wie in einem Mehrphasensystem der Sinus verwendet werden kann. Diese Gleichung gilt allgemein, unabhängig wie viele Phasen das System aufweist. In Gleichung 2 wird für \(m\) 3 eingesetzt. Der Winkel wird dadurch immer halb so groß, wie der eigentliche Winkel zwischen den Phasen wäre. Dadurch ist die Gegenkathete des Sinus die halbe Dreieckspannung. Mit Umstellung und Umwandlung des Wertes \(sin(\frac {\pi }{3})\) in \(\frac {\sqrt {3}}{2}\) erhält man schließlich den Faktor, um Stern- und Dreieckspannung umrechnen zu können.

In der Praxis wird die Sternspannung immer gekennzeichnet mit einem Sternsymbol als Index, bei der Dreieckspannung wird meistens auf ein Index verzichtet.

\begin {align} U_{\Stern }=\frac {U_{\Dreieck }}{\sqrt {3}}=\frac {U}{\sqrt {3}} \end {align}

Wie in der Abbildung 7 zu sehen, sind die Impedanzen der Verbraucher nun so geschaltet, dass es keinen Sternpunkt mehr gibt. In dieser Schaltung entsprechen die Strangspannungen nun den Außenleiter- oder Dreieckspannung.

Die Ströme zwischen den Strängen können aus der Knotenregel folgendermaßen ermittelt werden:

\begin {align} \underline {I}_{\mathrm {L1}}=\underline {I}_{\mathrm {L1L2}}-\underline {I}_{\mathrm {L3L1}} \\ \underline {I}_{\mathrm {L2}}=\underline {I}_{\mathrm {L2L3}}-\underline {I}_{\mathrm {L1L2}} \\ \underline {I}_{\mathrm {L3}}=\underline {I}_{\mathrm {L3L1}}-\underline {I}_{\mathrm {L2L3}} \end {align}

Wie auch bei der Sternschaltung kann im symmetrischen Fall gesagt werden, dass alle Impedanzen den gleichen Wert haben. Daraus ergibt sich für die Ströme im Strang:

\begin {align} \underline {I}_{\mathrm {L1}}&=\underline {I}_{\mathrm {L1L2}}-\underline {I}_{\mathrm {L3L1}}=\frac {\underline {U}_{\mathrm {L1L2}}-\underline {U}_{\mathrm {L3L1}}}{\underline {Z}}=\frac {U_{\Stern }}{\underline {Z}}\cdot (1-\underline {a}^2-\underline {a}+1)=3\cdot \frac {U_{\Stern }}{\underline {Z}} \\ \underline {I}_{\mathrm {L2}}&=\underline {I}_{\mathrm {L2L3}}-\underline {I}_{\mathrm {L1L2}}=\frac {\underline {U}_{\mathrm {L2L3}}-\underline {U}_{\mathrm {L1L2}}}{\underline {Z}}=\frac {U_{\Stern }}{\underline {Z}}\cdot (\underline {a}^2-\underline {a}-1+\underline {a}^2)=3\cdot \underline {a}^2 \cdot \frac {U_{\Stern }}{\underline {Z}} \\ \underline {I}_{\mathrm {L3}}&=\underline {I}_{\mathrm {L3L1}}-\underline {I}_{\mathrm {L2L3}}=\frac {\underline {U}_{\mathrm {L3L1}}-\underline {U}_{\mathrm {L2L3}}}{\underline {Z}}=\frac {U_{\Stern }}{\underline {Z}}\cdot (\underline {a}-1-\underline {a}^2+\underline {a})=3\cdot \underline {a} \cdot \frac {U_{\Stern }}{\underline {Z}} \end {align}

Aus diesen Umformungen geht hervor, dass die Ströme sich nur durch den Drehoperator \(a\) unterscheiden. Äquivalent zu der Umrechnung von der Stern- zur Dreiecksspannung kann auch ein Verhältniss zwischen Strang- und Dreiecksstrom aufgestellt werden. Nach gleicher Herleitung, wie in Abb. 6 zu sehen, nur die Spannung durch die passenden Stromwerte ersetzt, ergibt sich folgendes Verhältnis:

\begin {align} I_{\mathrm {str}}=\sqrt {3}\cdot I_{\Dreieck } \end {align}

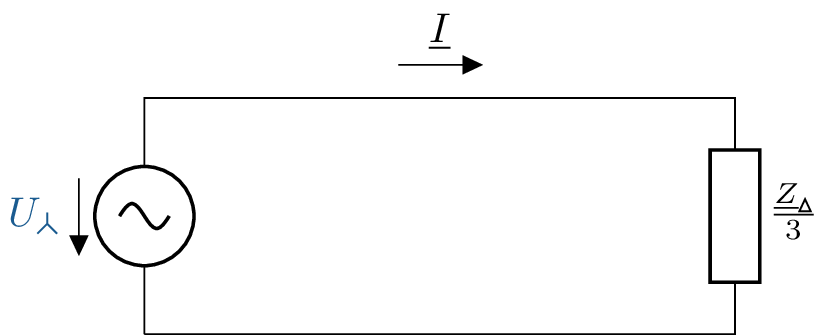
Mit den vorhandenen Angaben kann nun auch ein einphasiges ESB für die Dreieckschaltung aufgestellt werden (siehe Abb. 8).

1.3 Leistung im symmetrischen Drehstromnetz

Die Berechnung von Leistung basiert, wie in allen elektrischen System, auf der Gleichung \(P=U\cdot I\). Für das Drehstromsystem gilt die Besonderheit, dass die Leistung pro Phase berechnet werden muss. Liegt ein symmetrisches System vor, sind die Ströme und Spannungen pro Phase gleich und dementsprechend muss kann das Ergebnis aus einer Phase mit 3 multipliziert werden.

\begin {align} S&=3\cdot I_{\mathrm {str}}\cdot U_{\Stern }=3\cdot I_{\mathrm {str}}\cdot \frac {U_{\Dreieck }}{\sqrt {3}} \notag \\ &=3\cdot I_{\Dreieck }\cdot U_{\Dreieck }=3\cdot \frac {I_{\mathrm {str}}}{\sqrt {3}}\cdot U_{\Dreieck } \notag \\ &=\sqrt {3}\cdot U_{\Dreieck }\cdot I_{\mathrm {str}} \label {LeistungDrehstrom} \end {align}

Aus der Formel ?? geht hervor, dass es für die Leistungsberechnung keinen Unterschied macht, in welcher Schaltung gerechnet wird. Es muss nur darauf geachtet werden, mit welchen Spannungen und Strömen gerechnet wird (Dreieck oder Stern).

Anmerkung:

Die Notation der Indizes zu Dreiecks- oder Stern-Werten ist in der Literatur nicht eindeutig. Meistens wird für die Dreieckspannung (Außenleiterspannung) und dem Strangstrom kein Index angegeben \(U_{\Dreieck }=U\) und \(I_{str}=I\), sondern nur für die Sternspannung und dem Dreieckstrom.

Vergleicht man direkt die Leistung einer Dreieckschaltung und einer Sternschaltung, erhält man unterschiedliche Ergebnisse.

Für die Sternschaltung erhält man folgenden Wert: \begin {align} S=\sqrt {3}\cdot U\cdot I=\sqrt {3}\cdot U \cdot \frac {U_{\Stern }}{Z}=\frac {U^2}{Z} \end {align} Für die Dreieckschaltung erhält man wiederum: \begin {align} S=\sqrt {3}\cdot U\cdot I=\sqrt {3}\cdot U \cdot \sqrt {3}\cdot \frac {U}{Z}=3\cdot \frac {U^2}{Z} \end {align}

Demnach ist der Leistungsumsatz bei gleichen Impedanzen in einer Dreieckschaltung um den Faktor 3 größer als in einer Sternschaltung.

2 Unsymmetrische Komponenten

Die Grundlagen eines Drehstromsystems wurden im vorangegangenen Kapitel erläutert. Es wurde jedoch stets vorausgesetzt, dass sowohl die Erzeugung als auch die Verbraucher symmetrisch sind. Nun soll betrachtet werden, wie sich das System verhält, wenn Unsymmetrien vorliegen. Es bleibt jedoch erstmal dabei, dass die Generatorseite symmetrisch und im Stern verschaltet ist. Bleibt die Erzeugung star, können drei unterschiedliche Schaltungsarten vorliegen:

• Vierleiternetz in Sternschaltung
• Dreileiternetz in Sternschaltung
• Dreileiternetz in Dreieckschaltung

2.1 Vierleiternetz in Sternschaltung

Der Aufbau eines Vierleiternetz in Sternschaltung wurde als ESB in Abb. 3 dargestellt. Der Rückleiter wird dabei an die beiden Sternpunkte angeschlossen und verbindet damit Generator- und Verbraucherseite. Dadurch, dass die Sternspannung symmetrisch sind (aus der Vorgabe, dass die Generatorseite symmetrisch ist), sind auch die Verbraucherspannungen spannungssymmetrisch. Die Ströme hingegen weichen durch die unterschiedlichen Impedanzen von einander ab. So ist der Strom im Rückleiter in der Regel ungleich Null.

\begin {align} \underline {I}_\mathrm {N}=\underline {I}_{\mathrm {L1}}+\underline {I}_{\mathrm {L2}}+\underline {I}_{\mathrm {L3}} \end {align}

Logischerweise kann dann auch nicht mehr die Leistung so berechnet werden, wie in Formel ?? dargestellt. Es muss nun jeder Leiter einzeln berechnet und schließlich addiert werden.

\begin {align} \underline {S}=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+\underline {I}^*_{\mathrm {L3}}\cdot \underline {U}_{\mathrm {L3}} \end {align}

2.2 Dreileiternetz in Sternschaltung

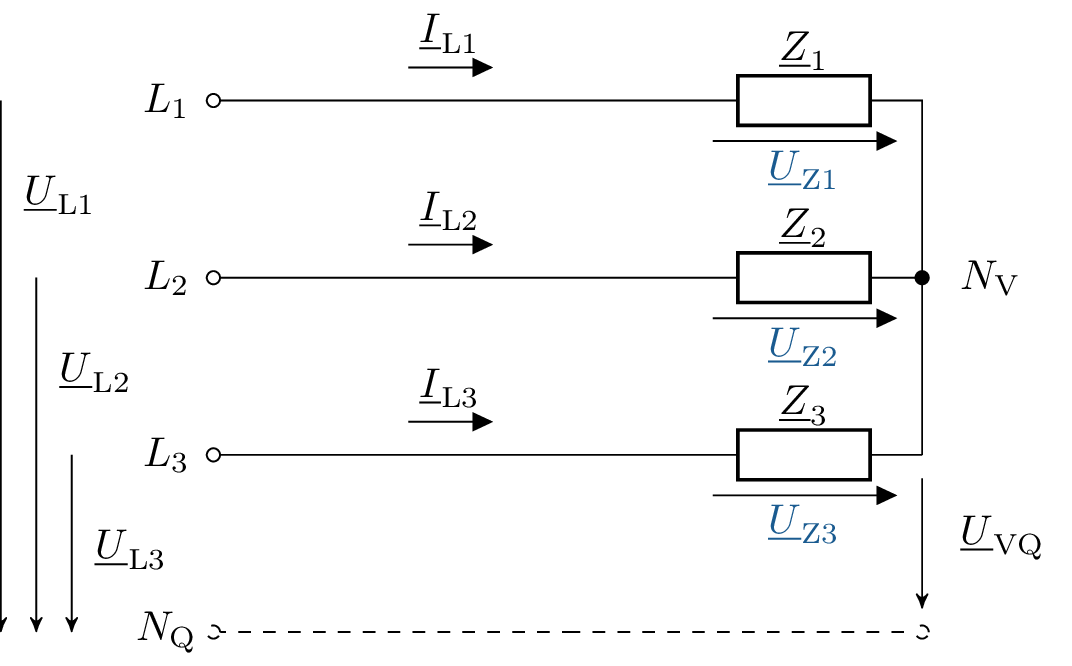
Prinzipiell gelten die gleichen Voraussetzungen im Dreileiternetz in Sternschaltung wie im Vierleiternetz. Der Unterschied liegt darin, dass der Strom nicht im Rückleiter abfließen kann und somit Auswirkung auf die anderen Leiter hat (s. Abb. 9). Aquivalent gilt das auch für die Spannung. Da kein Spannungsabfall im Rückleiter stattfindet, wirkt sich das auf die Spannung über den Verbrauchern aus. Es entstehet eine Spannungsdifferenz zwischen den beiden Sternpunkten, die mit den Spannungen über den Verbrauchern erst berechnet werden muss. Bei der Ermittlung der gesuchten Werte, können zwei Methoden angewendet werden. Für die erste Methode werden die Impedanzen rechnerisch in eine Dreieckschaltung umgewandelt, damit einfach und mit bekannten Methoden gerechnet werden kann. Denn in der Dreieckschaltung sind die Spannungen über die Impedanzen gleich den Leiterspannungen. Auch die Außenleiterströme lassen sich relativ einfach bestimmen.

Bei dem alternativen Lösungsweg können mit den bekannten Gesetzen nach Ohm und Kirchhoff Gleichungen aufgestellt werden mit den bekannten Werten des Systems. Für die Differenzspannung zwischen den beiden Sternpunkten kann folgende Gleichung aufgestellt werden:

\begin {align} \underline {U}_{VQ}=\frac {\frac {\underline {U}_{\mathrm {L1}}}{\underline {Z}_1}+\frac {\underline {U}_{\mathrm {L2}}}{\underline {Z}_2}+\frac {\underline {U}_{\mathrm {L3}}}{\underline {Z}_3}}{\frac {1}{\underline {Z}_1}+\frac {1}{\underline {Z}_2}+\frac {1}{\underline {Z}_3}}=\frac {\underline {U}_{\mathrm {L1}}\cdot \underline {Z}_2\cdot \underline {Z}_3+\underline {U}_{\mathrm {L2}}\cdot \underline {Z}_3\cdot \underline {Z}_1+\underline {U}_{\mathrm {L3}}\cdot \underline {Z}_1\cdot \underline {Z}_2}{\underline {Z}_1\cdot \underline {Z}_2+\underline {Z}_2\cdot \underline {Z}_3+\underline {Z}_3\cdot \underline {Z}_1} \end {align}

Die Leistung berechnet sich wie bekannt aus der Summer der Leistungen der einzelnen Phasen. Wichtig ist jedoch, dass nicht mit den Außenleiterspannung gerechnet wird, sondern mit den Spannungen über die Impedanzen:

\begin {align} \underline {S}=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {Z1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {Z2}}+\underline {I}^*_{\mathrm {L3}}\cdot \underline {U}_{\mathrm {Z3}} \end {align}

Theoretisch könnte mit dieser Formel die Berechnung erfolgen. Jedoch werden mit Messungen nicht die Werte gemessen, die für diese Formel benötigt werden. (Wie Messungen in einem Drehstromsystem durchgeführt werden, wird noch in einem folgenden Kapitel erklärt.) Wird die Formel für die Leistung wie folgt umgestellt, erkannt man, dass die Summe der Leiterströme Null ergeben müssen und somit der letzte Term wegfällt.

\begin {align} \underline {S}&=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+\underline {I}^*_{\mathrm {L3}}\cdot \underline {U}_{\mathrm {L3}}-\underline {U}_{\mathrm {VQ}}\cdot (\underline {I}^*_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}+\underline {I}^*_{\mathrm {L3}}) \notag \\ &=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+\underline {I}^*_{\mathrm {L3}}\cdot \underline {U}_{\mathrm {L3}} \end {align}

Hier sieht man, dass diese Formel für die Leistung die gleiche ist, wie im Vierleiternetz in Sternschaltung. Es kann jedoch hier eine Vereinfachung vorgenommen werden, da mit der Knotenregel ein Strom durch die beiden anderen Ströme ausgedrückt werden kann:

\begin {align} \underline {S}&=\underline {I}^*_{\mathrm {\mathrm {L1}}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+(-\underline {I}^*_{\mathrm {L1}}-\underline {I}^*_{\mathrm {L2}})\cdot \underline {U}_{\mathrm {L3}} \notag \\ &=(\underline {U}_{\mathrm {L1}}-\underline {U}_{\mathrm {L2}})\cdot \underline {I}^*_{\mathrm {L1}}+(\underline {U}_{\mathrm {L2}}-\underline {U}_{\mathrm {L3}})\cdot \underline {I}^*_{\mathrm {L2}} \notag \\ &=\underline {U}_{\mathrm {L3L1}}\cdot \underline {I}^*_{\mathrm {L1}}+ \underline {U}_{\mathrm {L2L3}}\cdot \underline {I}^*_{\mathrm {L2}} \end {align}

2.3 Dreileiternetz in Dreieckschaltung

Bei einer Dreieckschaltung steht kein Sternpunkt zur Verfügung, weshalb die Dreickschaltung nur in einem Dreileiternetz ausgeführt werden kann. In der Dreieckschaltung sind auf Grund der symmetrischen Einspeisung die Außenleiterspannungen ebenfalls symmetrisch. Die Ströme stellen sich je nach den Impedanzen ein und lassen sich wie bereits bekannt errechnen:

\begin {align} \underline {I}_{\mathrm {L1}}=\underline {I}_{\mathrm {L1L2}}-\underline {I}_{\mathrm {L3L1}} \\ \underline {I}_{\mathrm {L2}}=\underline {I}_{\mathrm {L2L3}}-\underline {I}_{\mathrm {L1L2}} \\ \underline {I}_{\mathrm {L3}}=\underline {I}_{\mathrm {L3L1}}-\underline {I}_{\mathrm {L2L3}} \end {align}

Die Summe der Außenleiterströme muss natürlich auch bei unsymmetrischen Strömen stets Null sein. Somit ergibt sich für die Leistungsberechnung die gleiche Rechnung wie bei der Sternschaltung im Dreileiternetz und somit auch die gleichen Umformungen.

\begin {align} \underline {S}&=\underline {I}^*_{\mathrm {L1L2}}\cdot \underline {U}_{\mathrm {L1L2}}+\underline {I}^*_{\mathrm {L2L3}}\cdot \underline {U}_{\mathrm {L2L3}}+\underline {I}^*_{\mathrm {L3L1}}\cdot \underline {U}_{\mathrm {L3L1}} \notag \\ &=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+\underline {I}^*_{\mathrm {L3}}\cdot \underline {U}_{\mathrm {L3}} \\ \notag \\ \underline {S}&=\underline {I}^*_{\mathrm {L1}}\cdot \underline {U}_{\mathrm {L1}}+\underline {I}^*_{\mathrm {L2}}\cdot \underline {U}_{\mathrm {L2}}+(-\underline {I}^*_{\mathrm {L1}}-\underline {I}^*_{\mathrm {L2}})\cdot \underline {U}_{L3} \notag \\ &=(\underline {U}_{\mathrm {L1}}-\underline {U}_{\mathrm {L2}})\cdot \underline {I}^*_{\mathrm {L1}}+(\underline {U}_{\mathrm {L2}}-\underline {U}_{\mathrm {L3}})\cdot \underline {I}^*_{\mathrm {L2}} \notag \\ &=\underline {U}_{\mathrm {L3L1}}\cdot \underline {I}^*_{\mathrm {L1}}+ \underline {U}_{\mathrm {L2L3}}\cdot \underline {I}^*_{\mathrm {L2}} \end {align}