Effektivwert

Durch die periodischen Spannungsverläufe weist jeder Zeitschritt einen anderen Spannungswert auf. Hierbei kann direkt lediglich der Spitzenwert angegeben werden, mit welchem jedoch nicht immer gearbeitet werden kann. Um eine nützliche Vergleichbarkeit von Spannungswerten zu gewährleisten wird der Effektivwert herangezogen. Der Effektivwert beschreibt beispielsweise die identische Leistung, welche an einem Widerstand anfallen würde, würde dieser an einer Gleichstromquelle angeschlossen sein. Zur weiteren Erklärung des Effektivwertes und der dafür erforderlichen Grundlagen werden in diesem Kapitel die folgenden Inhalte besprochen:

1 Grundlagen: Quadratischer Mittelwert und Additionstheorem

Neben dem arithmetischen Mittelwert, welcher in der Wechselstromrechnung zur Bestimmung des Mittelwerts genutzt wird, dient der quadratische Mittelwert der Bestimmung des Effektivwerts. Der quadratische Mittelwert (RMS - Root Mean Square) wird herangezogen, um die Vergleichbarkeit von Wechselspannungsgrößen zu ermöglichen. Hierbei wird eine Funktion f(t) zunächst quadriert. Darauffolgend wird der Mittelwert der quadrierten Funktion berechnet. Im letzten Schritt folgt das Radizieren des berechneten Mittelwertes. Der mathematische Zusammenhang des RMS wird in der Gleichung 1.

\begin {equation} RMS=\sqrt {\frac {1}{T}\int _{0}^T f(t)^2 dt} \label {GleichungEff1} \end {equation}

Bei der Bildung des Quadratischen Mittelwerts wird auch die Sinusfunktion quadriert. Als Hilfestellung wird ein Additionstheorem vorgestellt, mit welchem diese Berechnung vereinfacht werden soll. Additionstheoreme beziehen sich auf die Zusammenhänge der Trigonometzrie um eine Funktionen umzuformen. Die Umformung der quadratischen Sinusfunktion anhand des Additionstheorems wird in der Gleichung 2 dargestellt. Hier wird aus der quadratischen Sinusfunktion eine Funktion, welche lediglich von einer einfachen Cosinusfunktion abhängig ist.

\begin {equation} \sin ^2(x)=\frac {1}{2}(1-\cos (2x)) \label {GleichungEff2} \end {equation}

2 Amplitude

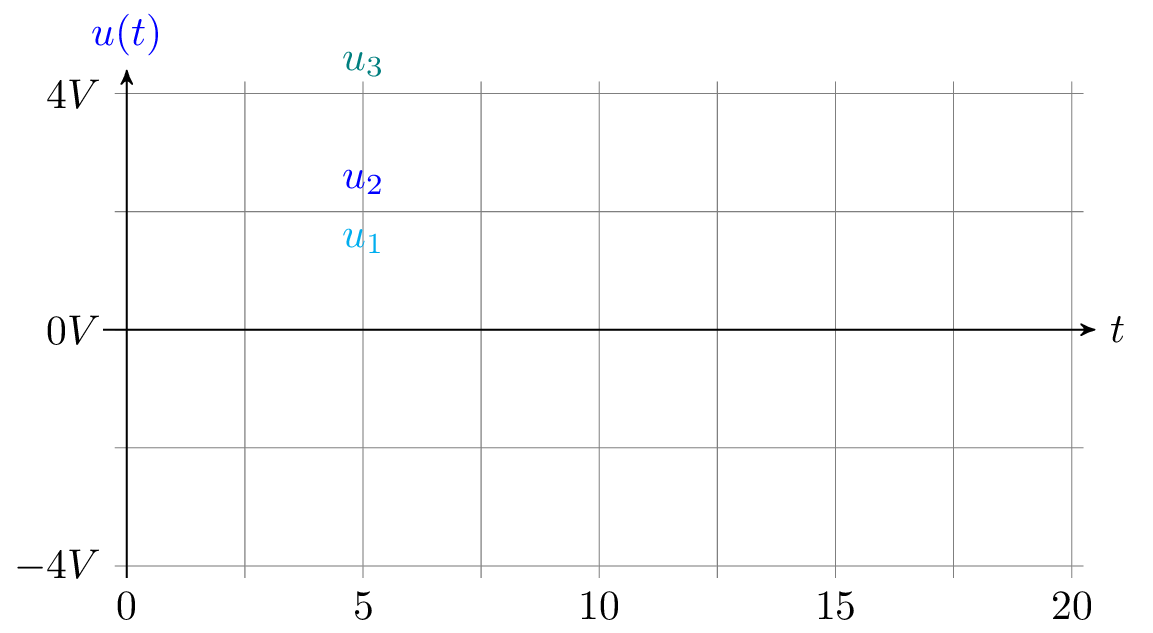
Die Ampltude einer Funktion beschreibt den maximalen Ausschalg während einer Periode. Bei einer Wechselspannung gibt der Amplitudenwert den höchsten momentanen Spannungswert der Spannung an. In der Abbildung 1 werden Spannungssignale mit einer Frequenz von \(50\,Hz\) und somit mit einer identischen Periodendauer von \(T=20\,ms\) dargestellt. Sie unterscheiden sich dabei beim Amplitudenwerten. Die Scheitelwerte der Amplituden der dargestellten Spannungen betrgen \(\hat {U}_1=1\,V\), \(\hat {U}_2=2\,V\) und \(\hat {U}_3=4\,V\). Die Amplitude ist eine Art Faktor für die Berechnung des Effektivwertes. So hängt die Höhe des Effektivwertes direkt von dem Amplitudenwert ab.

3 Kurvenform

Neben der Amplitude eines Signals ist die Kurvenform des Signals ausschlaggebend für den Effektivwert. Bei der Berechung des Effektivwerts wird der Scheitelfaktor \(C\) (engl. für crest factor) bestimmt, welcher mit dem Ampltudenwert verrechnet wird. In der Gleichung 3 wird die Beziehung zwischen dem Amplitudenwert und den Effektivwert über den Scheitelfaktor angegeben.

\begin {equation} \hat {U} = C \cdot U_\mathrm {Eff} \label {GleichungKur1} \end {equation}

Dieser Scheitelfaktor beträgt für Sinussignale \(C_S=\sqrt {2}\), für Dreiecksignale \(C_D=\sqrt {3}\) und für Rechtecksignale \(C_R=1\). Somit beträgt der Effektivwert einer Sinusspannung etwa \(70,7\) Prozent des Scheitelwerts der Amplitude. Neben dem Scheitelfaktor als Zusammenhang zwischen Scheitelwert und Effektivwert findet noch der Formfaktor \(F\) Anwendung. Der Formfaktor wird als Quotient aus dem Effektivwert und dem Gleichrichtwert definiert.

4 Effektivwert

Der Effektivwert, beispielsweise einer Sinusspannung, soll für die Leistungsaufnahme als ein Momentanwert verwendet werden, welcher die gleiche Leistungsaufnahme bewirkt, die dem Leistungswert einer Gleichspannung unter vergleichbaren Gegebenheiten entsprechen würde. Der Effektivwert ist auch beim Ohm’schen Gesetz und bei den Kirchhoffschen Gesetzen anwendbar und somit für alle grundlegenden Gesetze geeignet.

Anhand eines Wechselstromsignales \(i(t)\) soll die Berechnung des Effektivwertes erläutert werden. Wird die Definition des Stromsignales in die Gleichung 4 eingesetzt, so ergibt sich:

\begin {equation} f(t) = i(t) = \hat {I} \cdot \sin (\omega t) \quad \rightarrow \quad I_\mathrm {Eff}=\sqrt {\frac {1}{T}\int _{0}^T {\hat {I}}^2 \cdot \sin ^2(\omega t) dt} \label {GleichungEff3} \end {equation}

Die Quadratur des Scheitelwerts ist nicht zeitabhängig und kann vor das Integralzeichen gezogen werden. Außerdem kann der Faktor aus dem Additionstheorem aus dem Integral gezogen werden, sodass die nochfolgende Gleichung 5 entsteht:

\begin {equation} I_\mathrm {Eff}=\sqrt {\frac {\hat {I}^2}{2T}\int _{0}^T {1-\cos (2\omega t) dt}} \label {GleichungEff4} \end {equation}

Nach der Differenzregel können Differenzen in einem Integranden gesondert bestimmt werden. Auf diese Weise werden in der nachfolgenden Gleichung 6 die Integrale für die beiden Operanden der Differenz seperat bestimmt.

\begin {equation} \text {mit} \quad \int _0^T 1 dt = T \quad \text {und} \quad \int _0^T \cos (2 \omega t) dt = 0 \label {GleichungEff5} \end {equation}

Durch das Auflösen des Integrals entsteht:

\begin {equation} I_\mathrm {Eff} = \sqrt {\frac {\hat {I}^2}{2T}\cdot (T - 0)} \label {GleichungEff6} \end {equation}

Hier lässt sich die Periodendauer \(T\) aus dem Zähler und dem Nenner kürzen, sodass folgender Zusammenhang entsteht:

\begin {equation} I_\mathrm {Eff} = \sqrt {\frac {\hat {I}^2}{2}} \label {GleichungEff7} \end {equation}

Nun wird noch aus dem Zähler und dem Nenner getrennt die Wurzel gezogen. Der selbe Zusammenhang lässt sich so auch für die Spannung definieren:

\begin {equation} I_\mathrm {Eff} = \frac {\hat {I}}{\sqrt {2}} \qquad \text {und} \qquad U_\mathrm {Eff} = \frac {\hat {U}}{\sqrt {2}} \label {GleichungEff8} \end {equation}

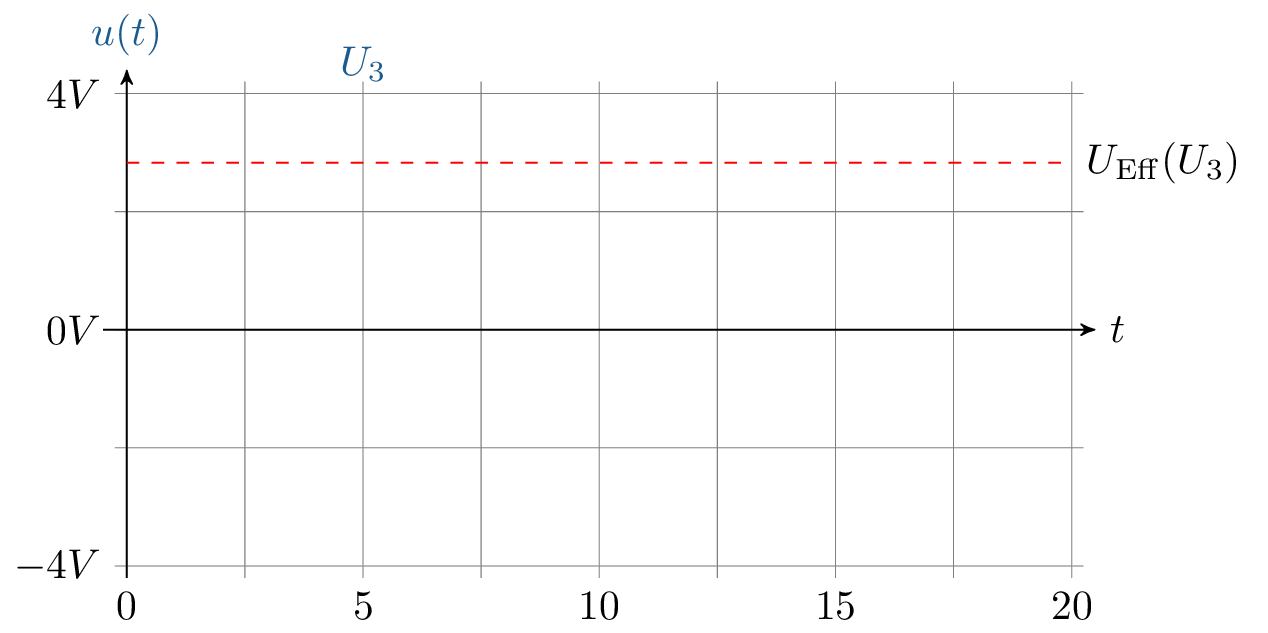
In der Abbildung 2 wird eine Sinusspnnung mit einem Amplitudenwert von \(4\,V\) dargestellt. Dazu wird der zu der Sinusspannung zugehörige Effektivwert bei \(4\,V/\sqrt {2}\) eingezeichnet. Vergleichbar verhält es sich mit den Spannungen im Haushalt. So würde bei einer Spannungsmessung im Haushalt ein Effektivwert von \(230\,V\) angezeigt werden. Der Amplitudenwert der eigentlich anliegenden Wechselspannung beträgt dabei allerdings \(230\,V\cdot \sqrt {2}\) also \(325\,V\).