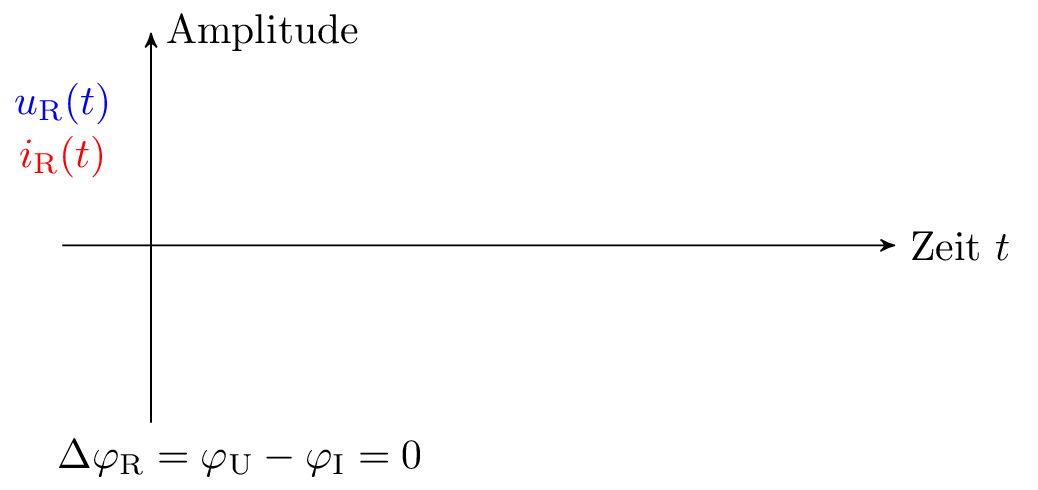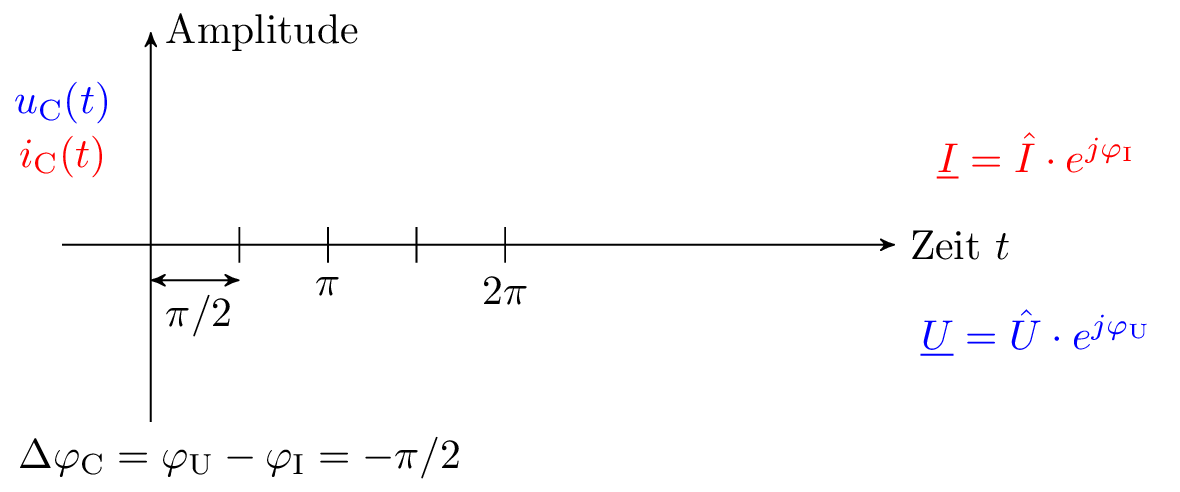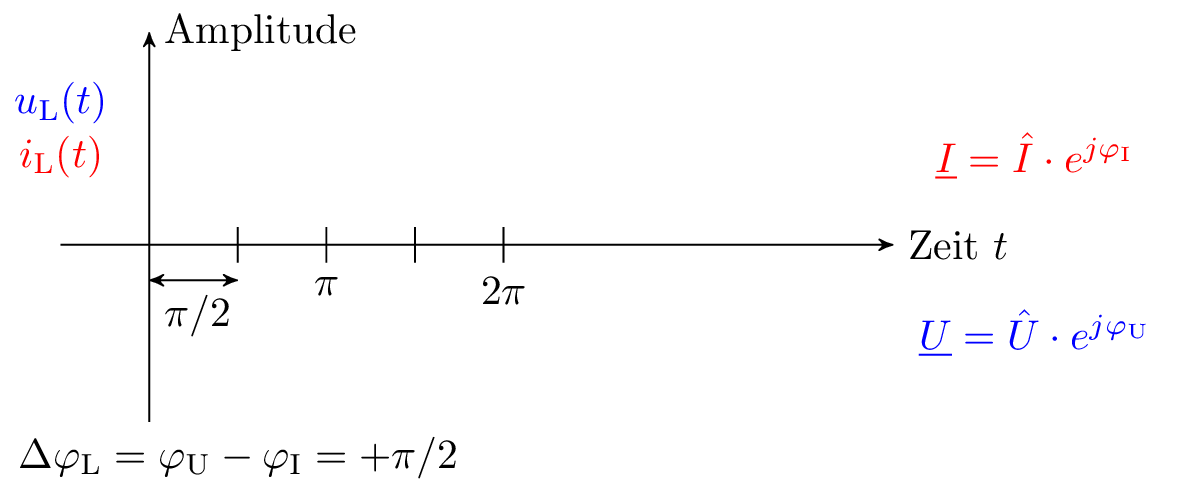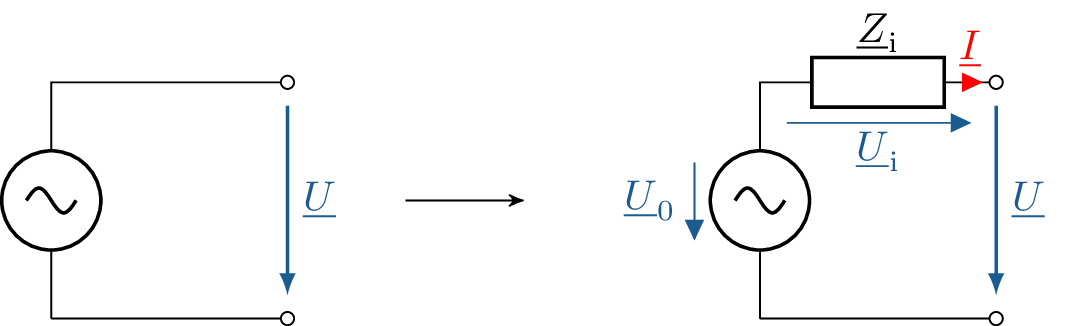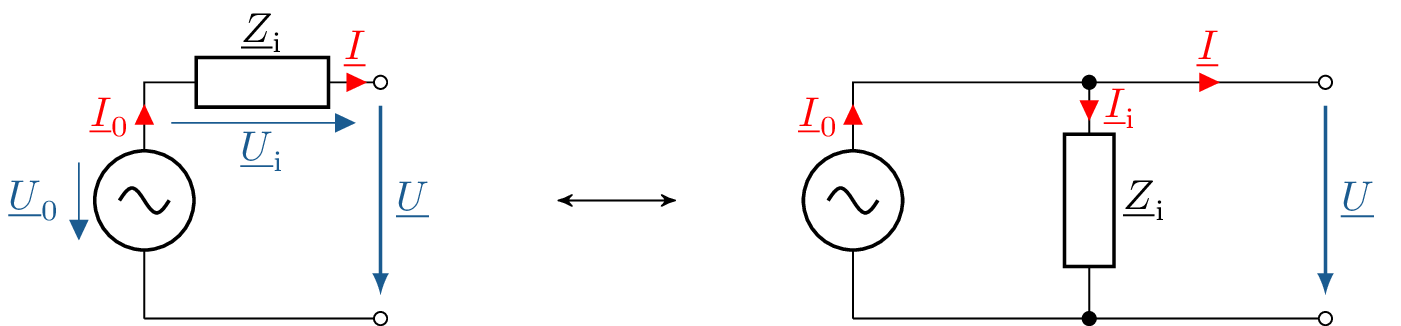Komplexe Wechselstromrechnung
In Gleichstromnetzwerken wird mit konstanten Spannungsquellen und Stromquellen gearbeitet. Im Gegensatz dazu kommen bei der komplexen Wechselstromrechnung Quellen mit sinusförmigen Wechselgrößen zum Einsatz. Die elektrische Analyse von Komponenten in einem Wechselspannungsnetzwerk erfolgt komplex. Die komplexen Spannungen U und Ströme I erzeugen zeitabhängige Spannungswerte u(t) und Stromwerte i(t). Die Gleichung 1 beschreibt den angegebenen Zusammenhang zwischen komplexen und zeitabhängigen Strom- und Spannungswerten für einen ohmschen Widerstand.
\begin {equation} \underline {U} = \underline {Z}_\mathrm {R} \cdot \underline {I} \quad \rightarrow \quad u(t) = R \cdot i(t) \label {GleichungURIKomplex} \end {equation}
Abgesehen von der komplexität der Wechselstromrechnungen, gelten weiterhin die Regeln zur Berechnung elektrischer Netzwerke, wie Maschen- und Knotenregeln, das Verhalten von Reihen- und Paralellschaltungen und die Knotenpotentialanalyse sowie die Maschenstromanalyse. Bei all diesen Beispielen ist darauf zu achten, mit den komplexen Wechselgrößen zu rechnen. Für die Erläuterung von elektrische Netzwerken mit komplexen Wechselgrößen werden im Folgenden diese Tehmengebiete näher betrachtet:
Lernziele: Wechselstromrechnung
Die Studierenden
- kennen die komplexe Impedanz und die komplexe Attmitanz.
- verstehen das Verhalten eines Widerstandes, eines Kondensators und einer Spule an einer Wechselspannung.
- kennen Wechselquellen und die dazugehörigen Umwandlungsvorschriften.
1 Impedanz und Attmitanz in der komplexen Ebene
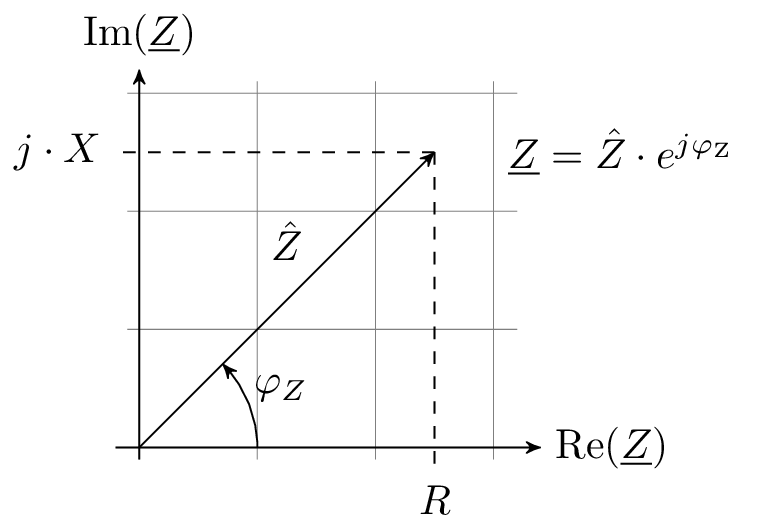
Durch eine Phasenverschiebung zwischen der Spannung und dem Strom kommt es zu einer Erzeugung eines Blindanteils der Impedanz. Der Blindanteil lässt sich jedoch auf der reellen Achse nicht darstellen, weshalb die reelle Achse um eine imaginäre Achse erweitert wird, welche gemeinsam die komplexe Ebene bilden. Die Abbildung 1 zeigt den Zeiger der komplexen Impedanz in der komplexen Ebene mit Imaginäranteil und Realanteil.
So besteht auch die komplexe Impedanz Z nach Gleichung 2 aus einem Realteil und aus einem Imaginärteil. Der Realteil besteht aus dem ohmschen Anteil, welcher den Wirkwiderstand einer Impedanz darstellt. Der Wirkwiderstand wird auch als Resistanz R bezeichnet. Zweiter Bestandteil der Impedanz ist der Imaginärteil, welcher auch als Reaktanz X bezeichnet wird. Die Reaktanz eines elektrischen Netzwerkes setzt sich beisplielsweise aus den kapazitiven und induktiven Auswirkungen zusammen und wird mit der imaginären Einheit j versehen. Die Einheit der komplexen Impedanz ist wie in der Gleichstromtechnik Ohm \(\Omega \).
\begin {equation} Impedanz = Resistanz + j \cdot Reaktanz \quad \rightarrow \quad \underline {Z} = R + j \cdot X \label {GleichungImpedanz} \end {equation} \begin {equation} [\underline {Z}] = 1\ Ohm = 1\ \Omega \nonumber \end {equation}
Wie in der Gleichstromtechnik existiert ein Leitwert des elektrischen Widerstandes in der komplexen Wechselstromtechnik. Dieser Kehrwert der komplexen Impedanz wird als Admittanz Y bezeichnet (vlg. Gleichung 4). Die Einheit des komplexen Leitwertes bleibt wie in der Gleichstromtechnik Siemens S.
\begin {equation} R = \frac {1}{G} \quad \rightarrow \quad \underline {Z} = \frac {1}{\underline {Y}} \label {GleichungImpedanzAttmitanz} \end {equation}
Auch die Admittanz lässt sich in einen Wirkleitwert und einen Blindleitwert differenzieren. Der Wirkleitwert G der Admittanz wird als Konduktanz und der Blindleitwert B der Admittanz wird als Suszeptanz bezeichnet (vgl. Gleichung 5 ).
\begin {equation} Admittanz = Konduktanz + j \cdot Suszeptanz \quad \rightarrow \quad \underline {Y} = G + j \cdot B \label {GleichungAdmittanz} \end {equation}
\begin {equation} [\underline {Y}] = 1\ Siemens = 1\ S \nonumber \end {equation}
Merke: Komplexe Impedanz und komplexe Admittanz
Der Gleichstromwiderstand wird bei einer Wechselspannung zur komplexen Impedanz Z. Der Kehrwert des Widerstandes, der Leitwert, wird bei einer Wechselspannung zur komplexen Admittanz Y.
2 Komplexer Widerstand
Der komplexe Widerstand eines ohmschen Verbrauchers besteht aus dem Wirkannteil R und dem Blindanteil des des ohmschen Widerstandes. Der ohmsche Widerstand R verkörpert die Eigenschaft leitfähiger Materialien elektrische Leistung in thermische Leistung umzuwandeln. Der Blindanteil des Widerstands wandelt die Leistung der Wechselströme nicht in Wärme um. Der Blindanteil des elektrischen Widerstands wird als \(X_\mathrm {R}\) beziechnet. Da der ideale elektrische Widerstand allerdings rein ohmsch und damit rein Real wirkt, wird in der Regel oft einfach das Formelzeichen R verwendet. Die Gleichung 7 erklärt diese Zusammenhänge.
\begin {equation} \underline {Z}_\mathrm {R} = R + j \cdot X_\mathrm {R} \quad \rightarrow \quad X_\mathrm {R-ideal} = j \cdot 0\ \Omega \quad \rightarrow \quad \underline {Z}_\mathrm {R} = R \label {GleichungWid1} \end {equation}
An den zeitabhängigen Werten für die Spannung und den Strom ergeben sich die Zusammenhänge des idealen ohmschen Widerstandes nach Gleichung 8.
\begin {equation} \underline {U} = \underline {Z}_\mathrm {R} \cdot \underline {I} \quad \rightarrow \quad u(t) = R \cdot i(t) \label {GleichungWid2} \end {equation}
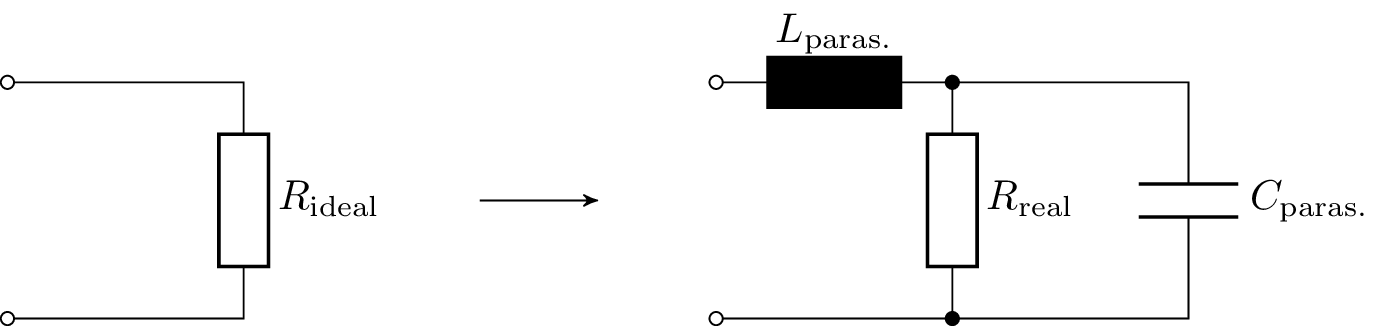
Ein idealer elektrischer Widerstand ist ein reiner Wirkwiderstand und weist keinerlei Blindwiderstandanteile auf. Der reale elektrische Widerstand ist mit parasitären Effekten behaftet. Die Schaltbilder eines idealen und eines realen elektrischen Widerstandes werden in der Abbildung 2 gegenübergestellt. Diese parasitären Effekte wirken sich induktiv, verdeutlicht durch die Spule, und kapazitiv, verdeutlicht durch die Kapazität, auf die Schaltung aus. Neben der Frequenzabhängikeit der parasitären Effekte, werden auch die Spannung und der Strom so aufgeteilt, dass nicht mehr die gesamte Leistung am Widerstand abfällt. die Impedanz des idealen elektrischenWiderstands ist nicht frequenzabhängig.
Zwischen der Spannung und dem Strom existiert beim idealen elektrischen Widerstand keine Phasenverschiebung. In der Abbildung 3 werden die Sinuswellen für die Spannung und den Strom an einem idealen Widerstand aufgetragen. Sie liegen ohne Phasenverschiebung übereinander, somit befinden sie sich in Phase.
Merke: Sinusschwingung an einem Widerstand
Der elektrische Widerstand weist zwischen der Wechselspannung und dem zugehörigen Wechselstrom keine Phasenverschiebung auf.
3 Kapazität
Der Kondesnator als Bauteil in der Elektrotechnik weist die Fähigkeit auf Energie zwischen den zwei Platten in dem elektrischen Feld zu speichern. Die Größe eines Kondensators wird in der Kapazität C angegeben. Die Einheit der Kapazität ist das Farad F. Die komplexe Impedanz eines Kondensators lässt sich nach Gleichung 9 berechnen. Im Gegensatz zum idealen Widerstand wirkt der ideale Kondensator im Wechselstromkreis nicht lediglich als Wirkwiderstand. Der reale Kondensator wirkt sowohl durch einen Wirkwanteil, als auch durch einen Blindanteil. Die Kreisfrequenz \(\omega \) ist frequenzabhängig. So ergeben sich bei hohen Frequenzen niedrige Impedanzwerte für den Kondensator. Andersherum ergeben sich hohe Impedanzwerte bei niedrigen Frequenzen. Der Blindanteil des Kondensators wirkt sich als kapazitive Reaktanz aus. Es kann beim Kondensator auch mit der komplexen Admittanz gerechnet werden. Die komplexe Admittanz ergibt sich aus dem kehrwert der komplexen Impedanz des Kondensators.
\begin {equation} \underline {Z}_\mathrm {C} = \frac {1}{j \omega C} \quad \rightarrow \quad \underline {Y}_\mathrm {C} = j \omega C \label {GleichungKap1} \end {equation}
Der ideale Kondensator wirkt rein im Blindanteil, so wird nach Gleichung 10 aus der komplexen Notation \(Z_C\) der Blindanteil des Kondensators \(X_C\) mit zeitabhängiger Spannung und Strom.
\begin {equation} \underline {U} = \underline {Z}_\mathrm {C} \cdot \underline {I} \qquad \qquad u(t) = \underline {X}_\mathrm {C} \cdot i(t) \label {GleichungKap2} \end {equation}
Es Wird davon ausgegangen, dass die Wechselspannung an einem Kondensator mit der Phasenverschiebung von 0° anliegt. Mit dieser Feststellung kann die verursachte Phasenverschiebung des Stromes am Kondensator nach Gleichung 11 festgelegt werden. Durch die Phasenverschiebung des Stromes gleicht der Verlauf einer Cosinusfunktion im Gegensatz zur Sinusfunktion der Spannung. Sollen sowohl die Spannung als auch der Strom durch die Sinusfunktion beschrieben werden, wird die Phasenverschiebung \(\Delta \varphi \) von \(\pi /2\) ins Argument mit aufgenommen.
\begin {equation} u(t) = \hat {U} \cdot \sin (\omega t) \qquad i(t) = \hat {I} \cdot \cos (\omega t) = \hat {I} \cdot \sin (\omega t + \pi /2) \label {GleichungKap3} \end {equation}
Bei Induktivitäten und Kapazitäten kommt es zu einer Phasenverschiebung zwischen der Wechselspannung und dem Wechselstrom. Beim Kondensator bedeutet dies, dass der Strom der Spannung um 90° (Gradmaß) voreilt. Der beschriebene Sachverhalt der Phasenverschiebung wird in der Abbildung 4 verdeutlicht. Der in rot dargestellte Strom an einem Kondensator erreicht den Maximalwert um \(2\pi \) (Bogenmaß) früher als der blau gefärbte Maximalwert der Spannung.
Merke: Sinusschwingung an einem Kondensator
An der idealen Kapazität eilt der Wechselstrom der Wechselspannung um 90° vor.
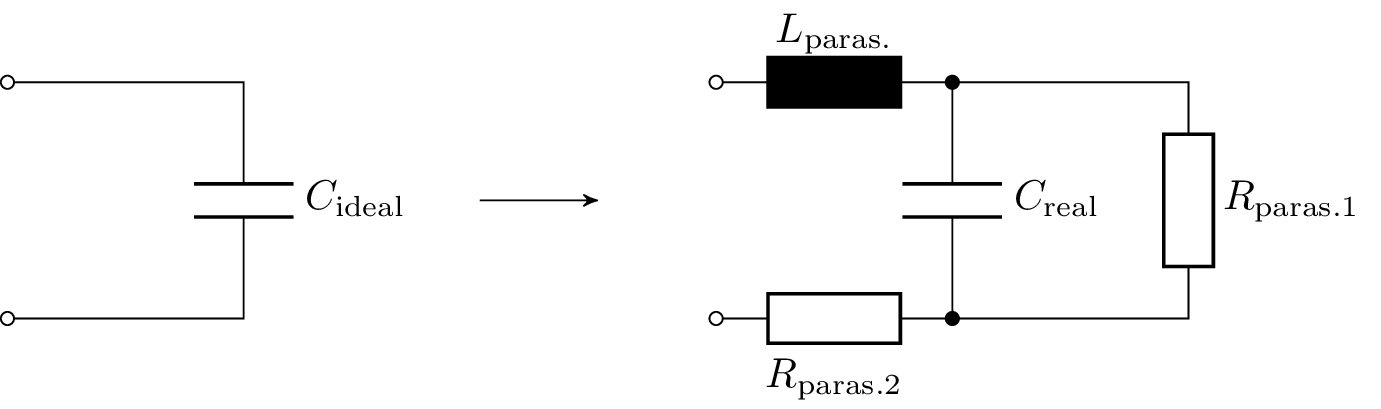
In der Regel wird mit idealen Bauteilen und deren Eigenschaften gerechnet. Jedoch weist der reale Kondensator, wie auch der zuvor beschriebene reale Widerstand, induktive und ohmsche parasitäre Effekte auf. Der ideale Kondensator wird in der Abbildung 5 dem realen Kondensator gegenübergestellt. Die Zu- und Ableitungen weisen induktive (\(L_\mathrm {paras.}\)) und ohmsche (\(R_\mathrm {paras.2}\)) Anteile auf. Außerdem ist der Kondensator einer ständigen Selbstentladung ausgesetzt. Diese Selbstentladung erfolgt symbolisch über den Paralellwiderstand \(R_\mathrm {paras.1}\).
4 Induktivität
Die Spule stellt ebenso einen Energiespeicher dar, wie der Kondensator. Nur wird bei der Spule die Energie nicht in einem elektrischen Feld gespiechert, sondern in einem magnetischen Feld nach den Gegebenheiten der Induktionsgesetze. Die Größe einer Spule wird in der Induktivität L angegeben. Die Einheit der Induktivität ist Henry H. Die komplexe Impedanz einer Spule ergibt sich aus der Imaginären Einheit j, der Kreisfrequenz \(\omega \) und der Induktivität L (vgl. Gleichung 12). die komplexe Admittanz wird durch den Kehrwert der Spulenimpedanz berechnet. Das führt zu Zusammenhängen, welche sich entgegen der Impedanzberechnungen bei Kapazitäten entwickeln. Bei hohen frequenzen werden die Impedanzen bei Spulen entsprechend ihrer Induktivität ebenfalls groß und bei niedrigen Frequenzen entsprechend gering.
\begin {equation} \underline {Z}_\mathrm {L} = j \omega L \quad \rightarrow \quad \underline {Y}_\mathrm {L} = \frac {1}{j \omega L} \label {GleichungInd1} \end {equation}
Ebenso wie beim Kondensator wirkt die ideale Spule rein als Blindanteil der Impedanz. In der Gleichung 13 wird auf der linken Seite die komplexe Notation der Spulenimpedanz \(Z_L\) verwendet. Auf der rechten Seite wird die Zeitfunktion lediglich mit der Schreibweise des Blindanteils der Spule \(X_L\) dargestellt.
\begin {equation} \underline {U} = \underline {Z}_\mathrm {L} \cdot \underline {I} \qquad \qquad u(t) = \underline {X}_\mathrm {L} \cdot i(t) \label {GleichungInd2} \end {equation}
Prinzipiell verhalten sich die Zeitfunktionen von Induktivitäten für die Spannung und den Strom vergleichbar, mit denen Zeitfunktionen von Kapazitäten. Lediglich die Phasenverschiebung des Stromes an Spulen ist der Phasenverschiebung der Kapazitäten entgegengesetzt. Die Phasenverschiebung \(\Delta \varphi \) zwischen der Spannung und dem Strom beträgt an einer Induktivität \(\pi /2\).
\begin {equation} u(t) = \hat {U} \cdot \cos (\omega t) = \hat {U} \cdot \sin (\omega t + \pi /2) \qquad i(t) = \hat {I} \cdot \sin (\omega t) \label {GleichungInd3} \end {equation}
Äquivalent zu der Phasenverschiebung an einem Kondensator existiert an der Induktivität ebenfalls eine Phasenverschiebung. Jedoch ist diese Phasenverschiebung des Stromes an der Induktivität der Phasenverschiebung der Kapazität entgegengerichtet. Im konkreten Fall in der Abbildung 6 wird gezeigt, dass der der Strom (rot) an einer Induktivität der Spannung (blau) nacheilt.
Merke: Sinusschwingung an einer Spule
Bei einer idealen Induktivität folgt der Wechselstrom der Wechselspannung um 90° nach.
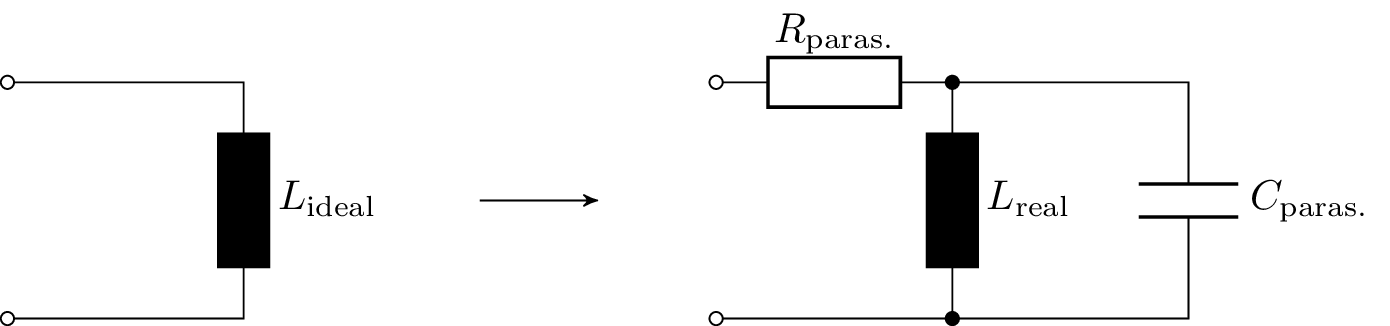
Wie auch der ohmsche Widerstand und der Kondensator weist die reale Spule parasitäre Effekte auf. Über den Spulendraht wirkt ein ohmscher Anteil (\(R_\mathrm {paras.}\)) auf die komplexe Impedanz der Spule ein. Zusätzlich erzeugt die Wicklung der Spule kapazitive Effekte (\(C_\mathrm {paras.}\)). In der Abbildung 7 wird das Ersatzschaltbild einer idealen Spule und einer realen Spule dargestellt.
5 Quellen von Wechselgrößen
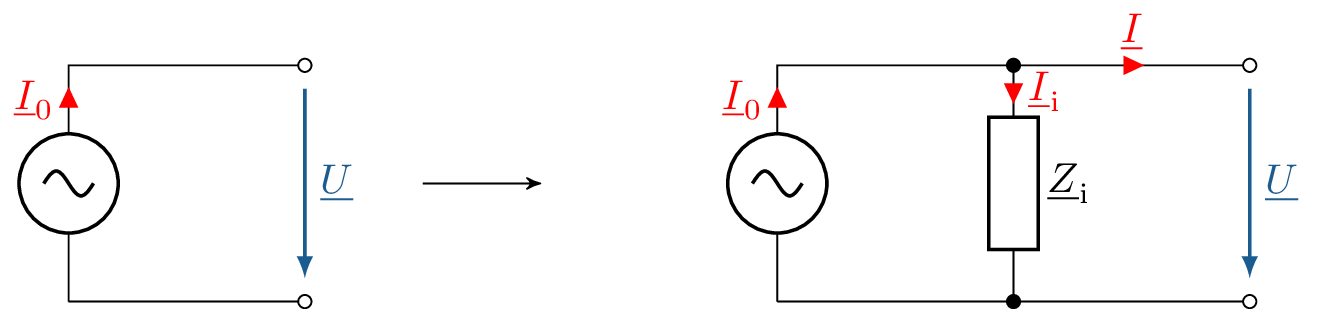
Wie bei Quellen von Gleichströmen und Gleichspannungen existieren Wechselquellen mit vergleichbaren Merkmalen. Bei der idealen Wechselspannungsquelle ist die Spannung eingeprägt. Die Wechselspannung ändert sich nicht mit der Abhängigkeit des Stromes, welcher durch sie hindurchfließt. Die ideale Wechselstromquelle stellt einen eingesprägten Strom zur Verfügung. Dieser wird nicht durch die angeschlossene Last beeinflusst. Die Schaltungssymbole einer idealen Wechselspannungsquelle und einer idealen Wechselstromquelle werden in der Abbildung 8 dargestellt.
Bei den beiden vorgestellten Wechselquellen werden ideale Quellen abgebildet. Reale Wechselquellen weisen wie auch die Quellen von Gleichspannungen und Gleichströmen Innenwiderstände auf. Diese Innenwiderstände prägen sich bei Quellen von Wechselgrößen als komplexe Impedanzen aus. Die reale Wechselspannungsquelle hat also eine komplexe Innenimpedanz \(\underline {Z}_\mathrm {i}\), welche mit einer idealen Wechselspannungsquelle in Serie geschaltet ist. Bei realen Wechselspannungsquellen ist die Ausgangsspannung \(\underline {U}\) von der angeschlossenen Last abhängig. Die Gegenüberstellung einer idealen und einer realen Wechselspannungsquelle ist in der Abbildung 9 dargestellt.
Die Ausgangsspannung einer realen Wechselspannungsquelle lässt sich nach Gleichung 15 bestimmen. Hier liegt die Wechselspannung der Wechselspannungsquelle nicht direkt an den Klemmen an. Sie wird durch die Spannung über die Innenimpedanz \(Z_\mathrm {i}\) reduziert.
\begin {equation} \underline {U} = \underline {U}_\mathrm {0} - \underline {Z}_\mathrm {i} \cdot \underline {I} \label {GleichungQuel1} \end {equation}
Reale Wechselspannungsquellen weisen gewisse Charakteristika ohne Last beim Leerlauf und bei einem Kurzschluss auf. Beim Leerlauf liegt zwischen den Klemmen eine unendlich große Impedanz. Es wird kein geschlossener Stromkreis gebildet und es stellt sich kein Stromfluss ein (Gleichung 16). Die gesamte Spannung der Wechselspannungsquelle liegt an den offenen Klemmen an, siehe Gleichung 17.
\begin {equation} \underline {I} = 0 \qquad \rightarrow \qquad \underline {U}_\mathrm {i} = \underline {I} \cdot \underline {Z}_\mathrm {i} = 0 \label {GleichungQuel2} \end {equation} \begin {equation} \underline {U}_\mathrm {0} - \underline {U}_\mathrm {i} - \underline {U} = 0 \qquad \rightarrow \qquad \underline {U} = \underline {U}_\mathrm {0} \label {GleichungQuel3} \end {equation}
Beim Kurzschluss geht die Impedanz zwischen den Klemmen gegen null und es fällt dort keine Spannung ab. So stellt sich ein größter möglicher Kurzschlussstrom ein, welcher lediglich durch die Innenimpedanz begrenzt wird (Gleichung 18). Die Spannungs der Wechselspannungsquelle wirkt so in Gänze über die Innenimpedanz (Gleichung 19). Der Kurzschlussstrom lässt sich nach Gleichung 20 aus dem Verhältnis aus der Spannung über die Innenimpedanz \(\underline {U}_\mathrm {i}\) und der Innenimpedanz \(\underline {Z}_\mathrm {i}\) bestimmen.
\begin {equation} \underline {U} = 0 \qquad \rightarrow \qquad \underline {I} = \underline {I}_\mathrm {k} \label {GleichungQuel4} \end {equation} \begin {equation} \underline {U}_\mathrm {0} - \underline {U}_\mathrm {i} - \underline {U} = 0 \qquad \rightarrow \qquad \underline {U}_\mathrm {i} = \underline {U}_\mathrm {0} \label {GleichungQuel5} \end {equation} \begin {equation} \underline {I}_\mathrm {k} = \frac {\underline {U}_\mathrm {i}}{\underline {Z}_\mathrm {i}} \label {GleichungQuel6} \end {equation}
Beispiel 1: Reale Spannungsquelle
-
Eine Reale Spannungsquelle (230 V, 50 Hz) verfügt nach der unten stehenden Abbildung über eine Innenimpedanz \(\underline {Z}_\mathrm {i}\), welche sich aus einer Spule \(L=20\ mH\) und einem ohmschen Widerstand \(R=10\ m\Omega \) zusammensetzt.
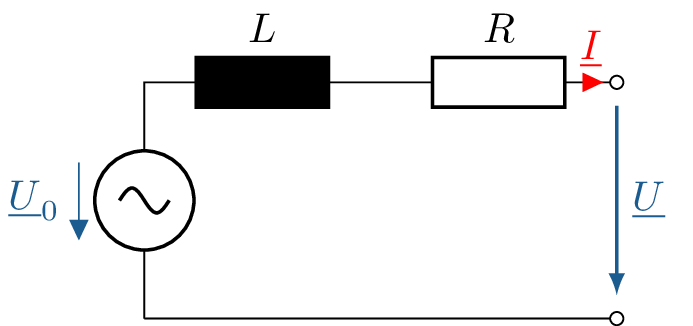
Abbildung 10: Beispiel. Wechselspannungsquelle mit einer Innenimpedanz aus einer Spule und einem Widerstand. Bestimmen Sie die Leerlaufspannung und den Kurzschlussstrom der Wechselspannungsquelle.
- \begin {align} \underline {U}_\mathrm {0} &= 230\ V \cdot e^{\mathrm {j}0^o} \nonumber \\ \underline {Z}_\mathrm {i} &= R + j X_L \nonumber \\ \underline {Z}_\mathrm {i} &= 0,01\ \Omega + j \cdot 2\pi \cdot 50\ Hz \cdot 20\ mH \nonumber \\ \underline {Z}_\mathrm {i} &= 0,01\ \Omega + j 6,28\ \Omega \nonumber \end {align}
Leerlaufspannung: \begin {align} \underline {U} &= \underline {U}_\mathrm {0} \nonumber \\ \underline {U} &= 230\ V \cdot e^{\mathrm {j}0^o} \nonumber \end {align}
Kurzschlussstrom: \begin {align} \underline {I}_\mathrm {k} &= \frac {\underline {U}_\mathrm {0}}{\underline {Z}_\mathrm {i}} \nonumber \\ \underline {I}_\mathrm {k} &= \frac {230\ V \cdot e^{\mathrm {j}0^o}}{0,01\ \Omega + j 6,28\ \Omega } \nonumber \\ \underline {I}_\mathrm {k} &= (0,058 - j36,6)\ A = 36,6\ A \cdot e^{-\mathrm {j}89,9^o} \nonumber \end {align}
Die reale Wechselstromquelle in der Abbildung 11 verfügt wie die Wechselspannungsquelle über eine Innenimpedanz \(\underline {Z}_\mathrm {i}\), wobei diese Innenimpedanz nicht wie bei der Wechselspannungsquelle in serie geschlatet ist, sondern parallel zu einer idealen Wechselstromquelle liegt. Der sich ergebende Ausgangsstrom \(\underline {I}\) der Quelle ist von der angeschlossenen Last, bzw. von der Ausgangsspannung \(\underline {U}\) abhängig.
Der Wechselstrom der idealen Wechselstromquelle wird durch einen Anteil durch die Innenimpedanz reduziert. Der Ausgangsstrom der realen Wechselstromquelle lässt sich über die Gleichung 21 bestimmen. Hier wird ausgehend vom Quellstrom \(\underline {I}_\mathrm {0}\) der ausgangsspannungsabhängige (\(\underline {U}\)) Wechselstromanteil \(\underline {I}_\mathrm {i}\) durch die Innenimpedanz \(\underline {Z}_\mathrm {i}\) abgezogen.
\begin {equation} \underline {I} = \underline {I}_\mathrm {0} - \underline {I}_\mathrm {i} = \underline {I}_\mathrm {0} - \frac {\underline {U}}{\underline {Z}_\mathrm {i}} \label {GleichungQuel7} \end {equation}
Wechselquellenumwandlung
Wechselstrom- und Wechselspannungsquellen können ineinander umgewandelt werden, wenn beide Wechselquellen den identischen Kurzschlussstrom und die gleiche Leerlaufspannung aufweisen.
Beide Wechselquellen sind äquivalent, wenn nach Gleichung 22 und Gleichung 23 das ohmsche Gesetz mit identischen Innenimpedanzen für die Wechselspannungsquelle und die Wechselstromquelle gilt.
\begin {equation} \underline {U}_\mathrm {0} = \underline {Z}_\mathrm {0} \cdot \underline {I}_\mathrm {0} \label {GleichungQuel8} \end {equation} \begin {equation} \underline {Z}_\mathrm {i} = \underline {Z}_\mathrm {0} \label {GleichungQuel9} \end {equation}
Hierbei soll der Kurzschlussstrom \(\underline {I}_\mathrm {K}\) gleich dem Quellstrom \(\underline {I}_\mathrm {0}\) der Wechselstromquelle sein, welcher identisch zu dem Ausgangsstrom \(\underline {I}\) ist. Die Ausgangswechselspannung \(\underline {U}\) der Wechselquellen enspricht der Leerlaufspannung \(\underline {U}_\mathrm {L}\).
\begin {equation} \underline {I} = \underline {I}_\mathrm {k} = \underline {I}_\mathrm {0} \qquad \text {und} \qquad \underline {U} = \underline {U}_\mathrm {L} = \underline {U}_\mathrm {0} \label {GleichungQuel10} \end {equation}
Beispiel 2: Wechselquellenumwandlung
- Gegeben ist eine reale Wechselspannungsquelle mit \(\underline {U}_\mathrm {0} = 20\ kV \cdot \mathrm {e}^{\mathrm {j}30^o}\) und \(\underline {Z}_\mathrm {0} = (0,01 + j \cdot 2)\ \Omega \). Wandeln Sie die
Wechselspannungsquelle in eine äquivalente Wechselstromquelle um, berechnen Sie
hierzu den Kurzschlussstrom.
- Kurzschlussstrom:
\begin {equation} \underline {I}_\mathrm {0} = \frac {\underline {U}_\mathrm {0}}{\underline {Z}_\mathrm {0}} = \frac {20\ kV \cdot \mathrm {e}^{\mathrm {j}30^o}}{(0,01 + j \cdot 2)\ \Omega } = (5,04 + j \cdot 8,64)\ kA \nonumber \end {equation}
6 Komplexer Spannungsteiler und komplexer Stromteiler
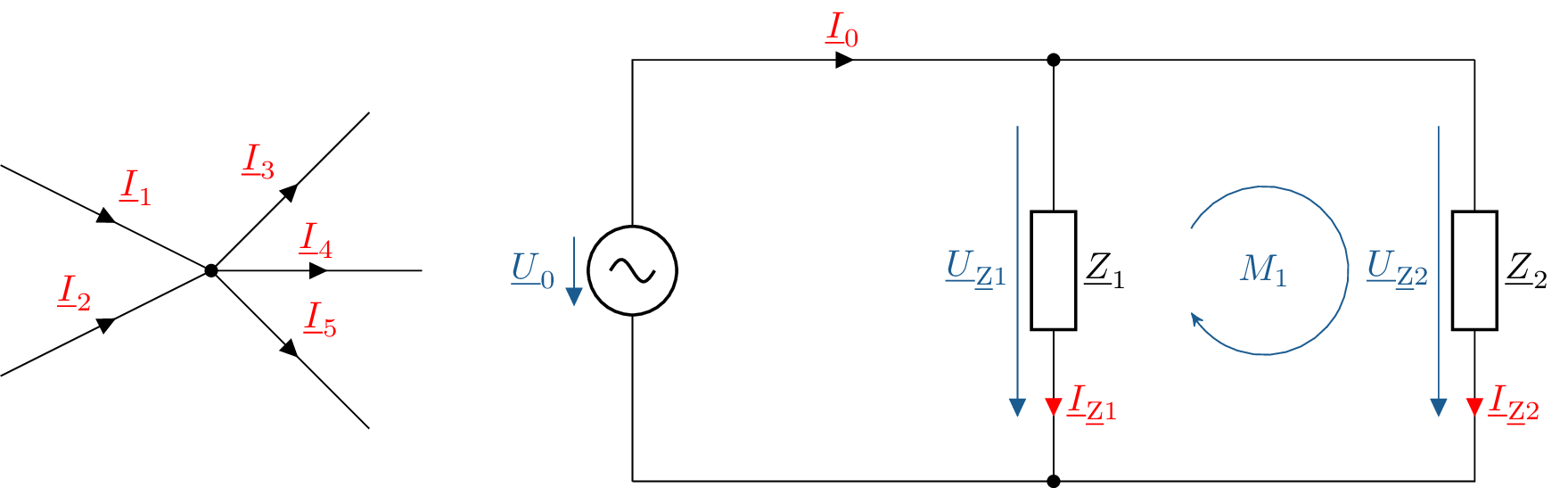
Wie bei der Betrachtung von Gleichstromnetzwerken gelten die Grundgesetze zur Analyse von Wechselstromnetzen. Die Knotenregel und die Maschenregel sind hier äquivalent anzuwenden. Der bereits vorgestellte Beispielknoten und die Beispielmasche werden in der Abbildung 13 mit komplexen Wechselgrößen noch einmal dargestellt. Hieraus resultiert die Ausformulierung der folgenden Gleichung 26 als Beispiel der komplexen Knotenregel:
\begin {equation} \sum _{k = 1}^{N}{\underline {I}_\mathrm {k}} = 0 = \underline {I}_\mathrm {1} + \underline {I}_\mathrm {2} - \underline {I}_\mathrm {3} - \underline {I}_\mathrm {4} - \underline {I}_\mathrm {5} \label {KnotenregelKomplex} \end {equation}
Sowie die Gleichung 27 als Beispiel der komplexen Maschenregel:
\begin {equation} \sum _\mathrm {k = 1}^{N}{\underline {U}_\mathrm {k}} = \underline {U}_\mathrm {Z2} - \underline {U}_\mathrm {Z1} = 0 \label {MaschengleichungKomplex} \end {equation}
Hier ist im Gegensatz zur Gleichstrombetrachtung, wo ausschließlich mit reellen Werten gerechnet wird, lediglich darauf zu achten, dass mit komplexen Wechselgrößen gearbeitet wird.
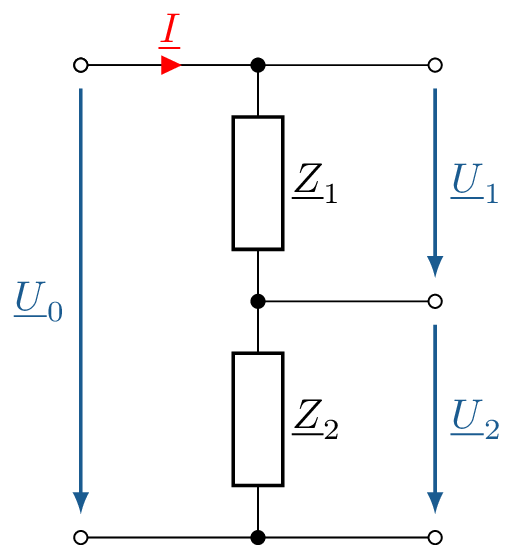
Der komplexe Spannungsteiler dient der Reduzierung einer Gesamtspannung z.B. der Anpassung eines Signalpegels an dem Eingangsspannungsbereich einer Messschaltung. In der Abbildung 14 wird ein komplexer Spannungsteiler aus zwei komplexen Impedanzen dargestellt. Die komplexe Gesamtspannung \(\underline {U}_\mathrm {0}\) wird über die beiden Impedanzen \(\underline {Z}_\mathrm {1}\) und \(\underline {Z}_\mathrm {2}\) in die Teilspannungen \(\underline {U}_\mathrm {1}\) und \(\underline {U}_\mathrm {2}\) aufgeteilt.
Die Gesamtspannung teilt sich im Verhältnis der komplexen Impedanzen auf (vgl. Gleichung 28). Basierend auf dem komplexen Strom \(\underline {I}\), welcher die gesamte Serienschaltung durchströmt, lassen sich die komplexen Teilspannungen \(\underline {U}_\mathrm {1}\) und \(\underline {U}_\mathrm {2}\) und ihre komplexen Impedanzen \(\underline {Z}_\mathrm {1}\) und \(\underline {Z}_\mathrm {2}\) im Verhältnis zu der komplexen Gesamtspannung \(\underline {U}_\mathrm {0}\) und der gesamten komplexen Impedanz \(\underline {Z}_\mathrm {1} + \underline {Z}_\mathrm {2}\) bestimmen.
\begin {equation} \underline {I} = \frac {\underline {U}_\mathrm {0}}{\underline {Z}_\mathrm {1} + \underline {Z}_\mathrm {2}} = \frac {\underline {U}_\mathrm {1}}{\underline {Z}_\mathrm {1}} = \frac {\underline {U}_\mathrm {2}}{\underline {Z}_\mathrm {2}} \label {GleichungTeiler1} \end {equation}
Durch das Umstellen der Gleichung 28 kann das komplexe Teilverhältnis \(\underline {T}\) für die Gleichung 29 aufgestellt werden:
\begin {equation} \underline {T} = \frac {\underline {U}_\mathrm {2}}{\underline {U}_\mathrm {0}} = \frac {\underline {Z}_\mathrm {2}}{\underline {Z}_\mathrm {1} + \underline {Z}_\mathrm {2}} \label {GleichungTeiler2} \end {equation}
Hier entspricht das Verhältnis aus der komplexen Teilspannung \(\underline {U}_\mathrm {2}\) und der komplexen Gesamtspannung \(\underline {U}_\mathrm {0}\) dem Verhältnis aus der komplexen Impedanz \(\underline {Z}_\mathrm {2}\) und der gesamten komplexen Impedanz der Serienschaltung \(\underline {Z}_\mathrm {1} + \underline {Z}_\mathrm {2}\). Das Aufstellen des komplexen Teilverhältnises funktioniert in gleicher Weise für die komplexe Teilspannung \(\underline {U}_\mathrm {1}\).
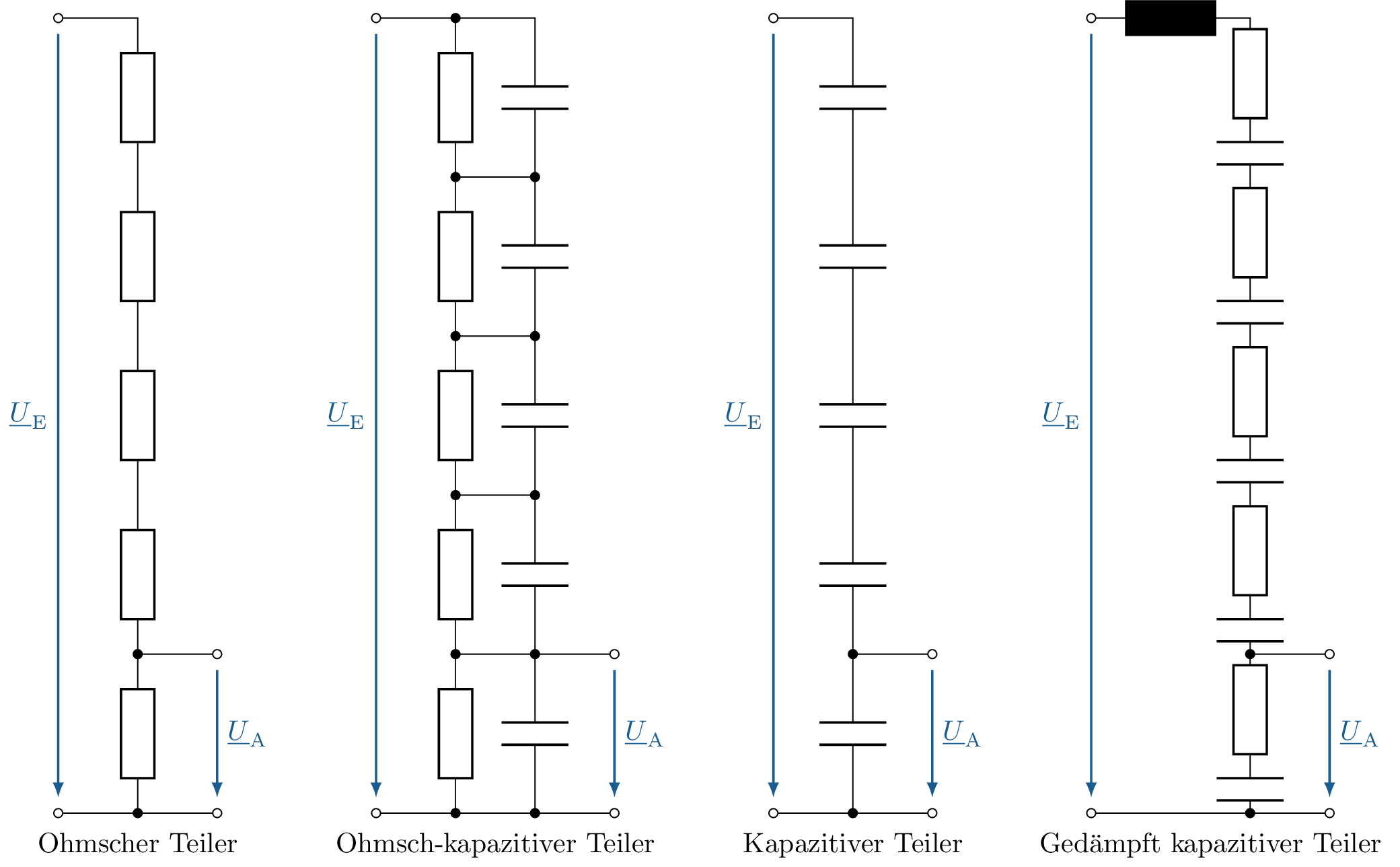
Der komplexe Spannungsteiler findet beispielsweise im ohmsch-kapazitiven Teiler in der Hochspannungstechnik Anwendung. In der Abbildung 15 werden vier verschiedene Teiler dargestellt, welche beispielsweise in der Hochspannungstechnik verwendet werden.
Neben dem ohmsch-kapazitiven Teiler werden noch der ohmsche Teiler, der kapazitive Teiler und der gedämpft kapazitive Teiler vorgestellt. Der ohmsche Teiler besteht rein aus ohmschen Widerständen, welche seriell verschaltet sind und der kapazitive Teiler besteht rein aus Kondensatoren. Der gedämpft kapazitive Teiler besteht aus mehreren Modulen mit einer vorgeschalteten Spule. Die Module setzten sich aus Reihenschaltungen aus einem ohmschen Widerstand und einem Kondensator zusammensetzten.
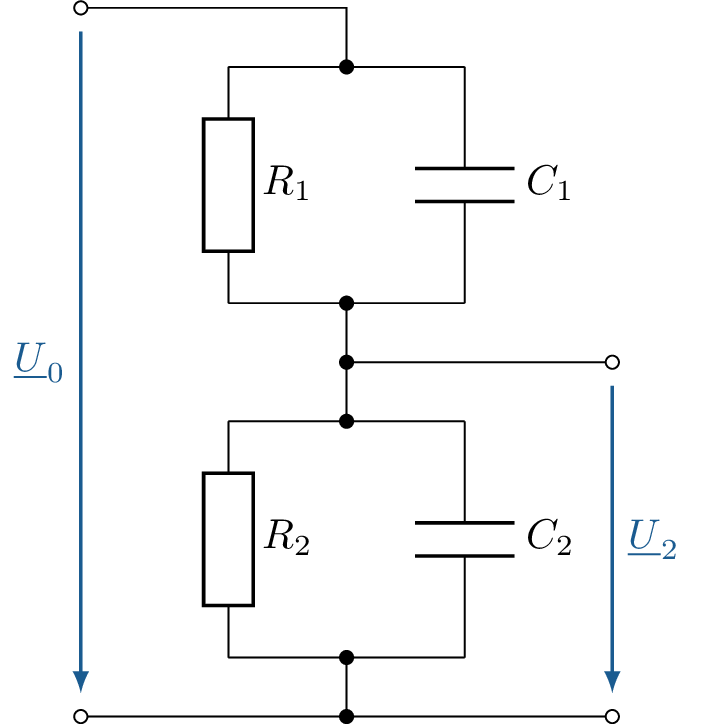
Das Einfache Beispiel eines solchen ohmsch-kapazitiven Teilers wird in der Abbildung 16 gezeigt. Der ohmsch-kapazitive Teiler setzt sich aus mindestens zwei in serie geschlateten Parallelschaltungen aus einem ohmschen Widerstand und einem Kondensator, einem sogennanten RC-Glied zusammen. In der Abbildung 16 besteht das erste RC-Glied aus dem Widerstand \(R_1\) und dem Kondensator \(C_1\). Das zweite RC-Glied besteht aus dem Widerstand \(R_2\) und Kondensator \(C_2\). Die komplexe Gesamtspannung \(\underline {U}_\mathrm {0}\) liegt über beide RC-Glieder an. Die komplexe Teilspannung \(\underline {U}_\mathrm {2}\) liegt über dem zweiten RC-Glied an. Das Teilverhältnis hat somit ohmsche und kapazitive Anteile. So liegt durch die Kapazität des Kondensators ein frequenzabhängiges Teilverhältnis vor.
Ein besonderer Zustand liegt vor, wenn der komplexe Spannungsteiler abgeglichen ist. Dieser Zustand beschreibt das identische Verhältnis der Bauteile zueinander. Dieser Zustand wird durch die Gleichung 30 beschrieben. Hier muss das Produkt aus dem Widerstand \(R_1\) und dem Kondensator \(C_1\) identisch mit dem Produkt aus dem Widerstand \(R_2\) und dem Kondensator \(C_2\) sein. Diese Abgleichbedingung lässt sich in der Praxis durch veränderliche Bauteile, wie Trimmkondensatoren, realisieren.
\begin {equation} R_1 \cdot C_1 = R_2 \cdot C_2 \label {GleichungTeiler3} \end {equation}
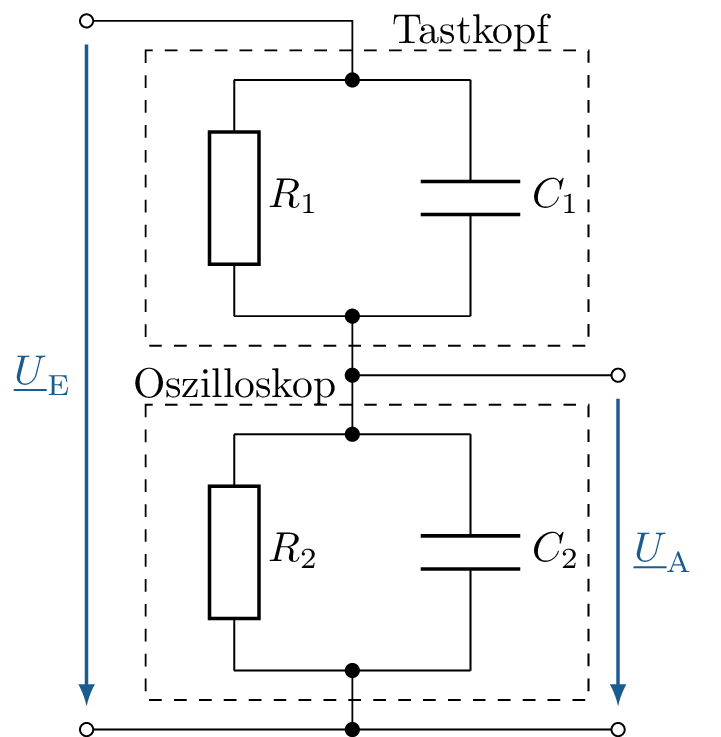
Ein weiteres Anwedungsbeispiel für einen ohmsch-kapazitiven Teiler ist der Tastkopf eines Oszilloskops. Solch ein Teiler wird in der Abbildung 17 vorgestellt. Im Prinzip unterscheid sich das Bild nicht erheblich vom ohmsch-kapazitiven Teiler. Jedoch sind hier das erste und das zweite RC-Glied von einander räumlich getrennt und mit einem Gehäuse umgeben. So steht das erste RC-Glied für den Tastkopf und das zweite RC-Glied für die beschaltung im Oszilloskop. Mit dem ohmsches Teilverhältnis: \begin {equation} \frac {\underline {U}_\mathrm {A}}{\underline {U}_\mathrm {E}} = \frac {R_\mathrm {2}}{R_\mathrm {1}+R_\mathrm {2}} \end {equation}
und dem kapazitiven Teilverhältnis: \begin {equation} \frac {\underline {U}_\mathrm {A}}{\underline {U}_\mathrm {E}} = \frac {C_\mathrm {2}}{C_\mathrm {1}+C_\mathrm {2}} \end {equation}
kann zum Abgleichen des Tastkopfes das ohmsche und das kapazitive Teilerverhältnis gleichgesetzt werden, da die Teilerverhältniss identisch sein müssen: \begin {equation} \frac {R_\mathrm {2}}{R_\mathrm {1}+R_\mathrm {2}} = \frac {C_\mathrm {2}}{C_\mathrm {1}+C_\mathrm {2}} \end {equation}
Die Abgleichbedingung nach Gleichung 30 gilt weiterhin. Über die verstellbare Kapazität \(C_1\) wird der Abgleich des Teilers vorgenommen.
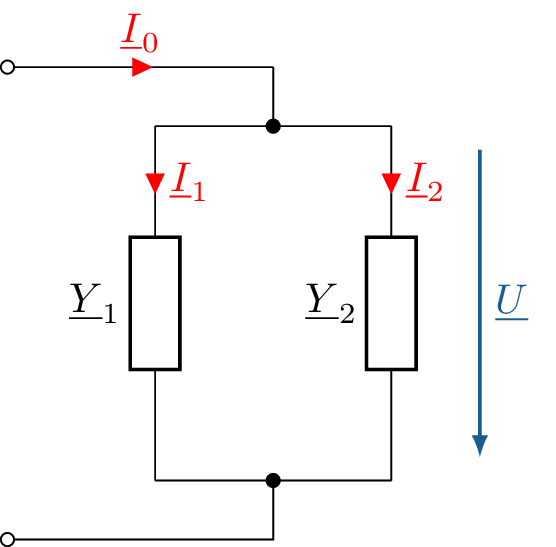
Der komplexe Stromteiler, wie er in der Abbildung 18 vorgestellt wird, teilt den komplexen Gesamtstrom \(\underline {I}\) auf in die Teilströme \(\underline {I}_\mathrm {1}\) und \(\underline {I}_\mathrm {2}\) auf. Die beiden Teilströme \(\underline {I}_\mathrm {1}\) und \(\underline {I}_\mathrm {2}\) durchfließen die Admittanzen \(\underline {Y}_\mathrm {1}\) und \(\underline {Y}_\mathrm {2}\).
Die komplexe Spannung \(\underline {U}\) lässt sich nach Gleichung 34 über das Verhältnis aus dem Gesamtstrom \(\underline {I}\) und der Gesamtadmittanz \(\underline {Y}_\mathrm {1} + \underline {Y}_\mathrm {2}\) oder aus den Verhältnissen der einzelnen Stromzweige:
\begin {equation} \underline {U} = \frac {\underline {I}_\mathrm {0}}{\underline {Y}_\mathrm {1}+\underline {Y}_\mathrm {2}} = \frac {\underline {I}_\mathrm {1}}{\underline {Y}_\mathrm {1}} = \frac {\underline {I}_\mathrm {2}}{\underline {Y}_\mathrm {2}} \label {GleichungStromteiler1} \end {equation}
Das Teilerverhältnis lässt sich nach Gleichung ?? für die beiden Stromzweige definieren:
\begin {align} \underline {T}_\mathrm {i1} = \frac {\underline {I}_\mathrm {1}}{\underline {I}_\mathrm {0}} = \frac {\underline {Y}_\mathrm {1}}{\underline {Y}_\mathrm {1}+\underline {Y}_\mathrm {2}} \label {GleichungStromteiler2} \\ \underline {T}_\mathrm {i2} = \frac {\underline {I}_\mathrm {2}}{\underline {I}_\mathrm {0}} = \frac {\underline {Y}_\mathrm {2}}{\underline {Y}_\mathrm {1}+\underline {Y}_\mathrm {2}} \label {GleichungStromteiler3} \end {align}
...