Im Modul 9
Aufgaben
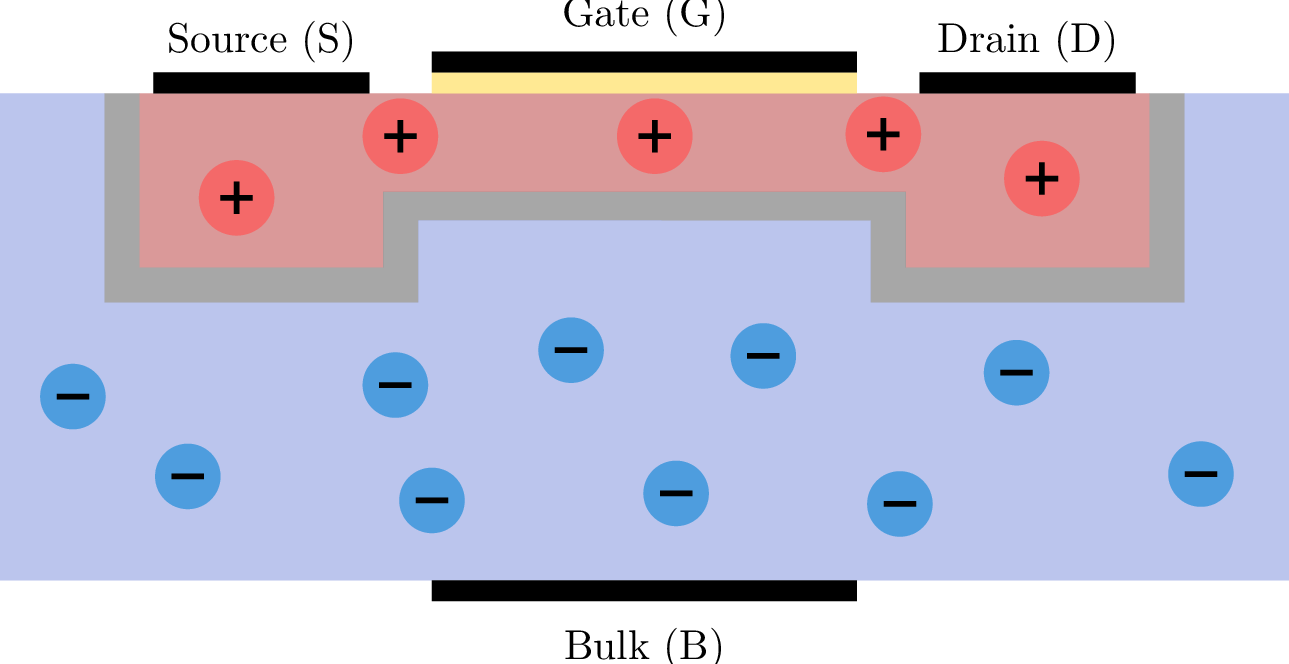
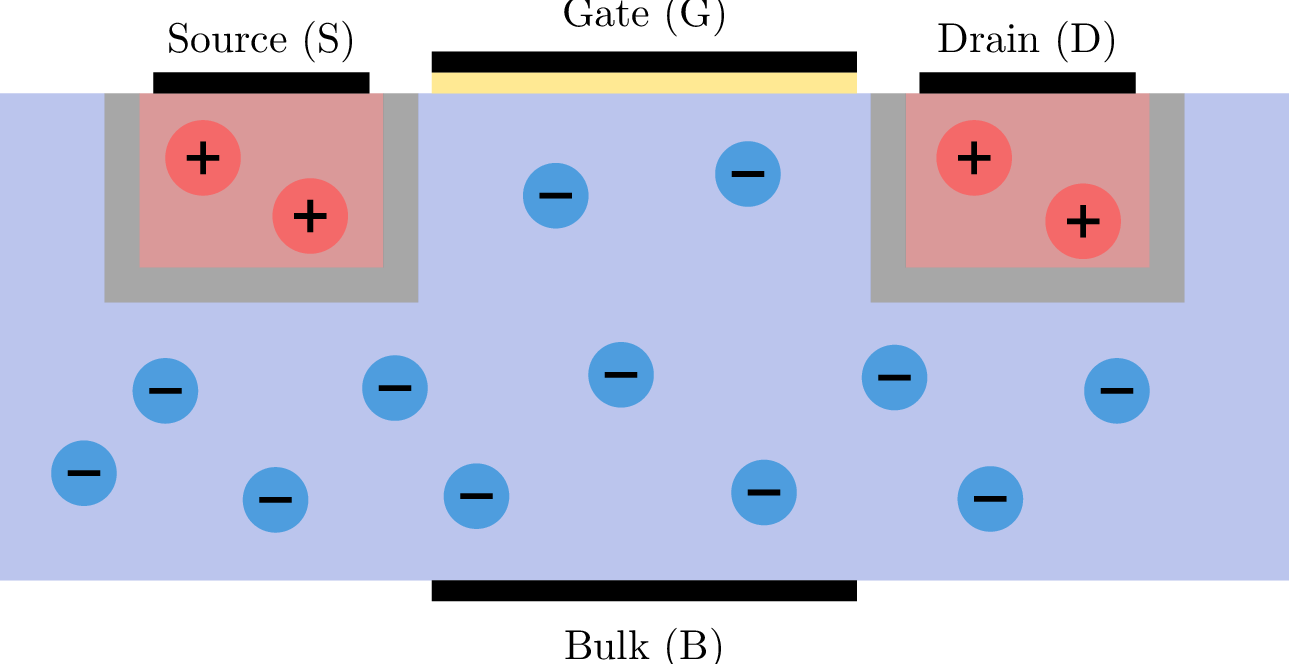
EinführungBeschreiben Sie ausführlich das Bändermodell von Festkörpern und seine Bedeutung für die Unterscheidung zwischen Leiter, Halbleiter und Isolator. Gehen Sie dabei insbesondere auf die folgenden Aspekte ein:
relevante Bänder und deren Besetzung mit Ladungsträgern.
die Bedeutung der Bandlücke und wie diese die elektrischen Eigenschaften von Materialien beeinflusst.
Einfluss von Temperaturänderungen auf die Leitfähigkeit.
Das Bändermodell erklärt die Energiezustände, die Elektronen in Festkörpern einnehmen können. In einem einzelnen Atom sind die Elektronenzustände diskrete Energielevel. Siehe: Abschnitt ??
Untersuchen Sie die Eigenschaften und die Bildung der Raumladungszone in pn-Übergängen von Halbleitern. Beantworten Sie die folgenden Aspekte in Ihrer Ausarbeitung:
Was ist die Raumladungszone und wie entsteht diese im pn-Übergang?
Wie ist der Verlauf des elektrischen Feldes im Halbleiter?
Welche inneren Vorgänge wirken auf die freien Ladungsträger?
Wie verändert sich die Raumladungszone bei einer angelegten Spannung in Durchlass- und Sperrrichtung?
Die RLZ ist eine schmale Region um den pn-Übergang herum, in der positive Ionen aus der n-Schicht und negative Ionen aus der p-Schicht verbleiben, nachdem die Diffusion abgeschlossen ist. In dieser Zone gibt es keine freien Ladungsträger, da die positiven und negativen Ladungen sich gegenseitig neutralisieren. Dadurch entsteht ein elektrisches Feld (\(\vec {E}\)), das sowohl einen Driftstrom erzeugt als auch die Diffusion von weiteren Ladungsträgern unterdrückt. Die Raumladungszone wirkt wie eine Sperrschicht und verhindert den Stromfluss in Sperrrichtung. Siehe: Abschnitt ??
Gegeben ist eine Reihenschaltung aus einer Gleichspannungsquelle, einem Widerstand und einer Siliziumdiode mit einer Schleusenspannung von \(U_\mathrm {S}=0,7\,\mathrm {V}\). Welche Spannung fällt näherungsweise über dem Widerstand \(R\) ab, wenn die Versorgungsspannung \(U_0=5\,\mathrm {V}\) beträgt?
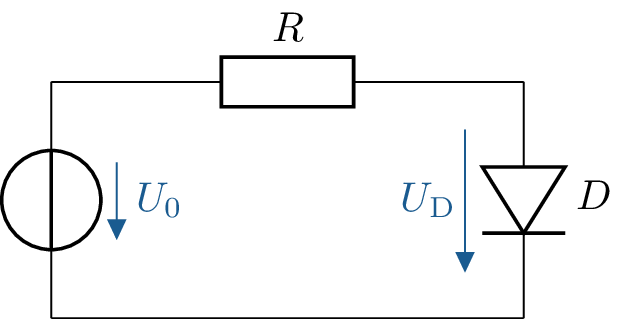
Da es sich um eine Siliziumdiode handelt, beträgt die Schleusenspannung und der daraus resultierende Spannungsabfall am Bauteil ungefähr \(0,6 \text { bis } 0,7\,\mathrm {V}\).
In der Reihenschaltung ergibt sich der folgende Zusammenhang: \begin {equation*} U_0 = U_\mathrm {R} + U_\mathrm {D} \end {equation*} \begin {equation*} U_\mathrm {R} = U_0 - U_\mathrm {D}= 5\,\mathrm {V} - 0,7\,\mathrm {V} = 4,3\,\mathrm {V} \end {equation*} Siehe: Abschnitt ??
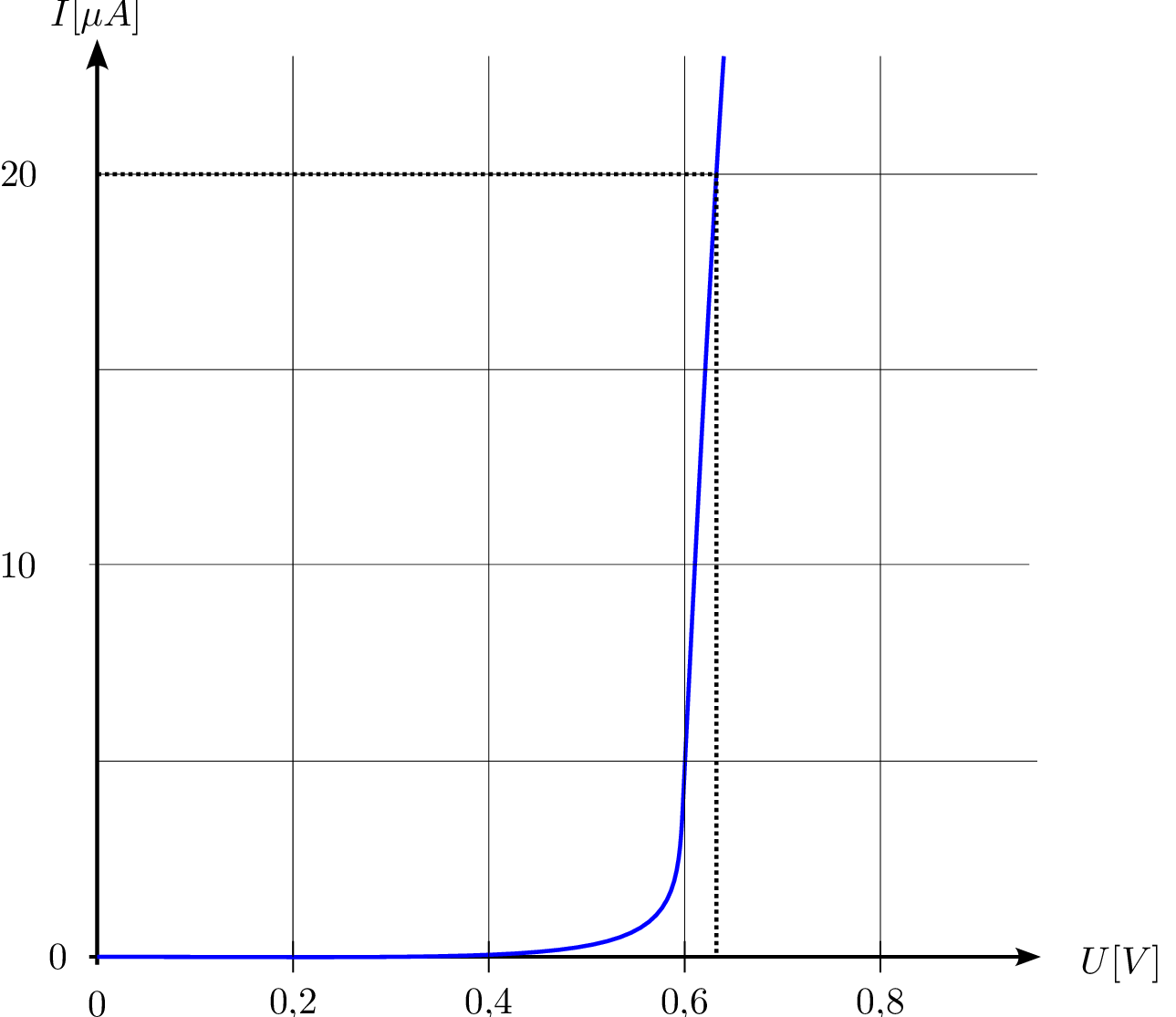
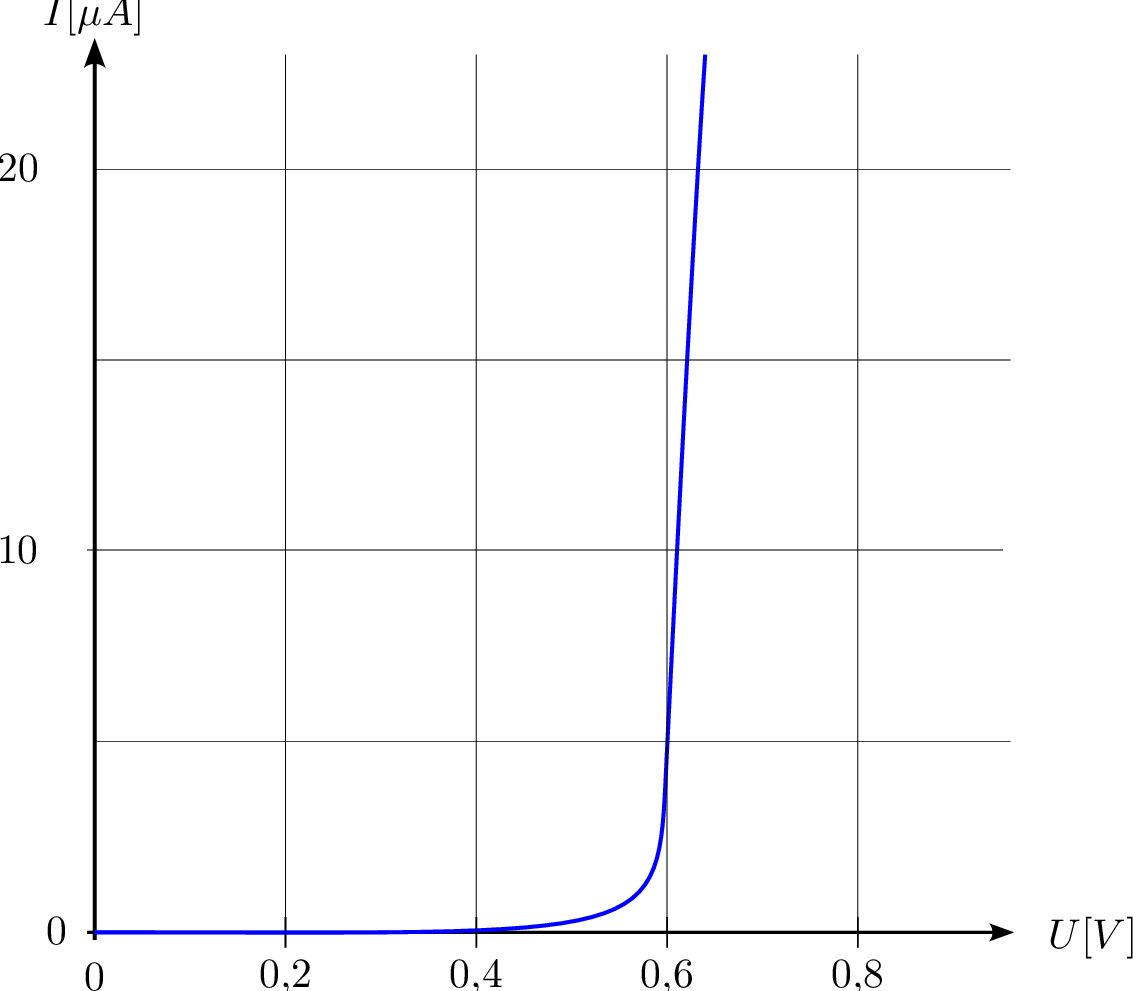
Eine Diode hat die folgende Kennlinie im Durchlassbereich. Sie wird in Reihe mit einer idealen Spannungsquelle \(U_0=1\,\mathrm {V}\) und einem Widerstand mit dem Wert von \(R=200\,\Omega \) geschaltet.
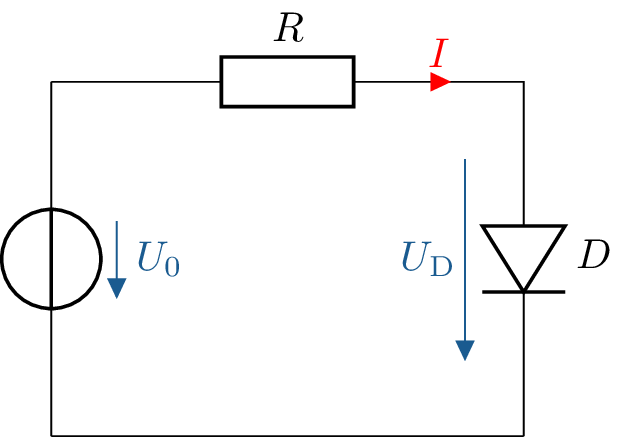
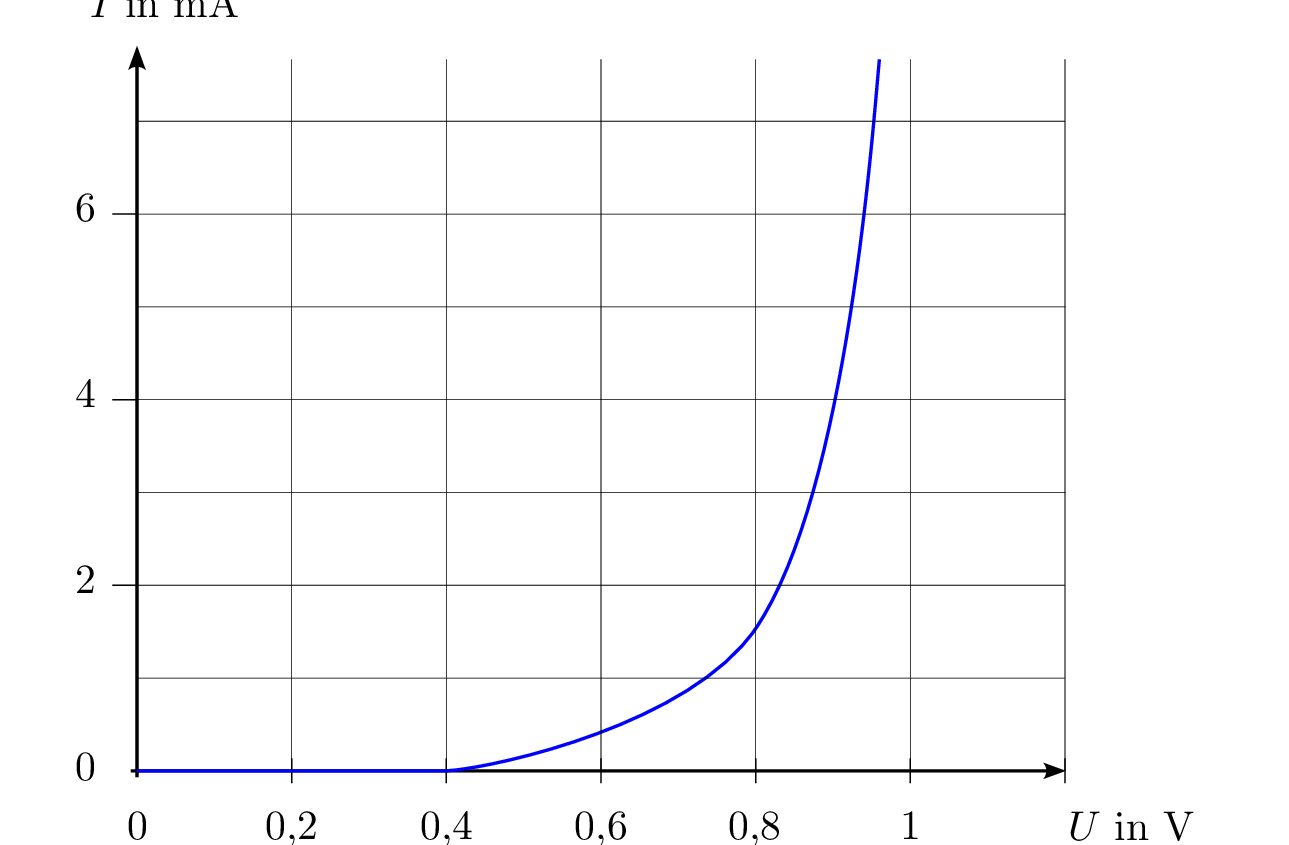
Welcher Strom \(I\) und welche Spannung \(U_\mathrm {D}\) stellen sich ein? Lösen Sie das Problem graphisch.
Welche elektrische Leistung wird an der Diode umgesetzt?
Wie muss \(R\) gewählt werden, damit sich ein Strom von \(3\,\mathrm {mA}\) einstellt?
Im ersten Schritt wird die Wirkung der Spannungsquelle auf den Widerstand \(R\) betrachtet. Bei
\(U_0=1\,\mathrm {V}\) fließen durch den Widerstand \(R\) ein Strom von \(I_\mathrm {R}=\frac {U_0}{R}=\frac {1\,\mathrm {V}}{200\,\Omega }=5\,\mathrm {mA}\). Es kann die Widerstandgerade vom Ursprung
aus zu dem Punkt (\(1\,\mathrm {V}\), \(5\,\mathrm {mA}\)) eingezeichnet werden (linke Abbildung).
Gemäß des Aufbaus der Schaltung muss die Widerstandsgerade im nächsten Schritt gespiegelt
werden, es entsteht die rechte Darstellung. Der Schnittpunkt beider Linien entspricht dem
Arbeitspunkt (\(U_\text {AP}\), \(I_\text {AP}\)), dieser lautet: (\(0,75\,\mathrm {V}\), \(1,2\,\mathrm {mA}\)).
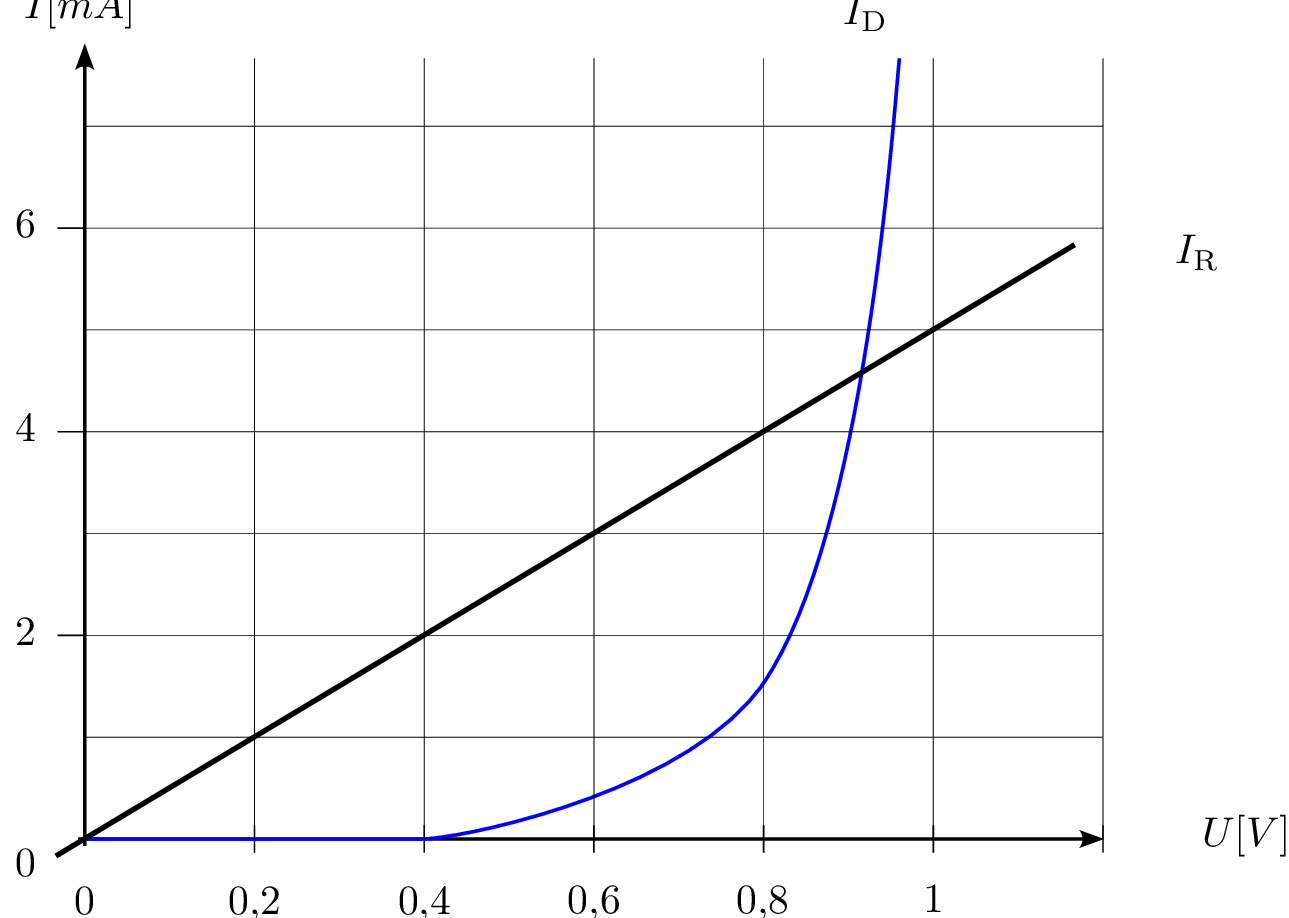
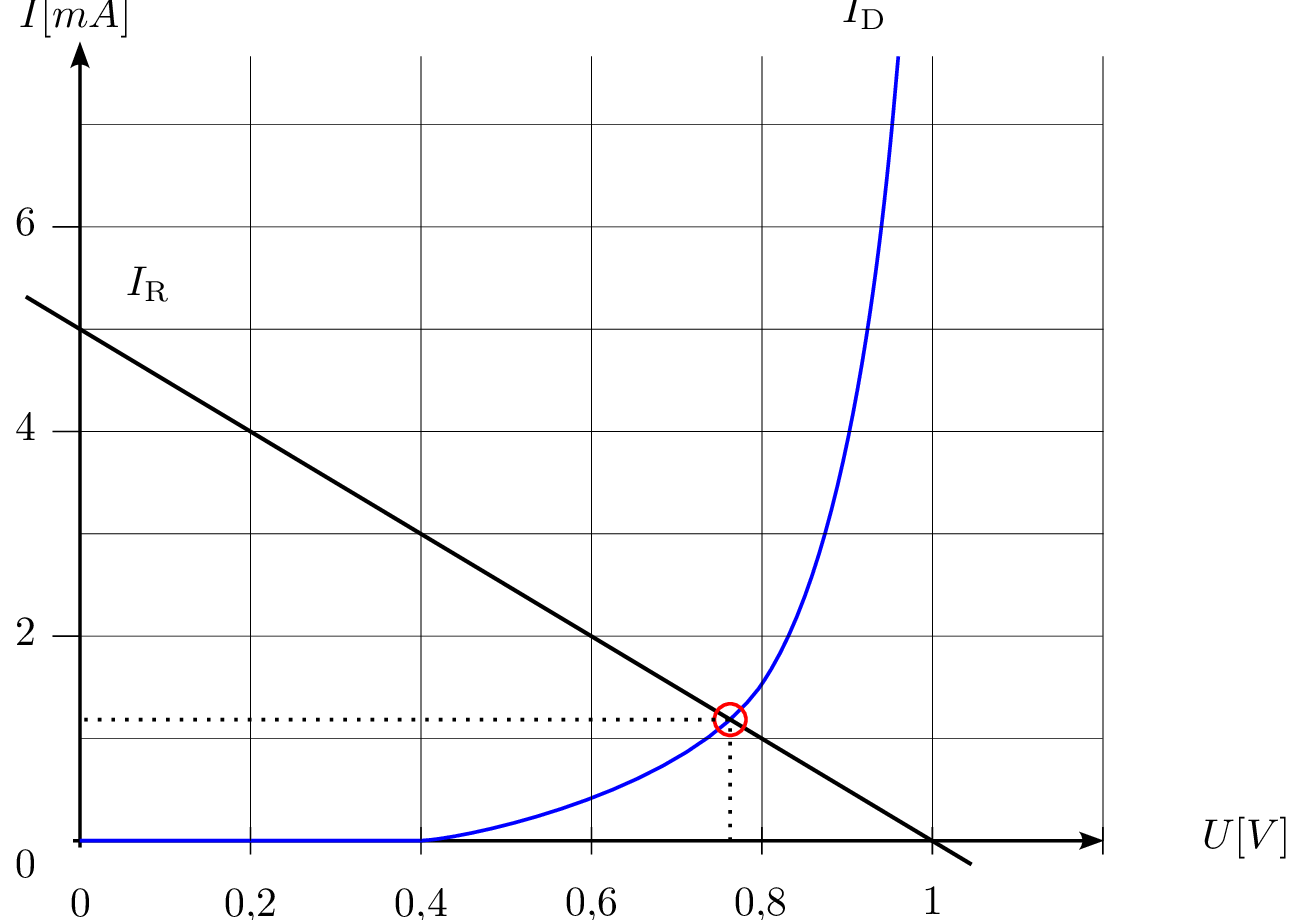
Die Leistung ergibt sich aus dem zuvor ermittelten Arbeitspunkt. \begin {equation*} P = U_\text {AP} \cdot I_\text {AP} = 0,75 \, \text {V} \cdot 1,2 \, \text {mA} = 0,9 \, \text {mW} \end {equation*}
Ausgehend vom Punkt (\(1\,\mathrm {V}, 0\,\mathrm {mA}\)) zum Schnittpunkt mit der Diodenkennlinie bei \(I=3\,\mathrm {mA}\) ergibt sich die gesuchte Widerstandsgerade.
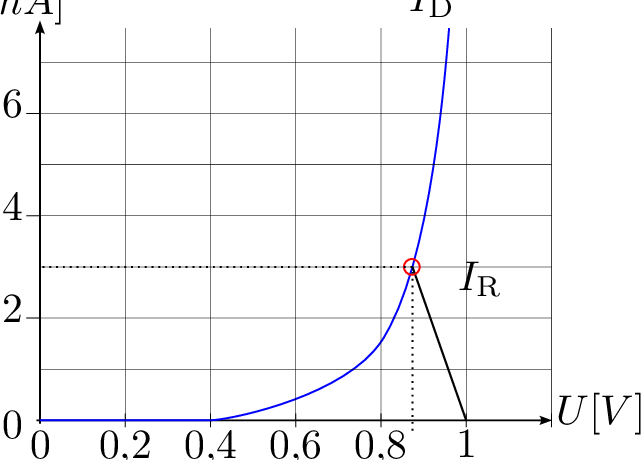
Es kann der Schnittpunkt (\(0,86\,\mathrm {V}, 3\,\mathrm {mA}\)) abegelesen werden.
\begin {gather*} U_\mathrm {R} = U_0 - U_\mathrm {D} = 1 \, \mathrm {V} - 0,86 \, \mathrm {V} = 0,14 \, \mathrm {V} \\ I = 3 \, \mathrm {mA} \\ R = \frac {U_{\text {R}}}{I} = \frac {0,14 \, \text {V}}{3 \, \text {mA}} = 46,67 \, \Omega \end {gather*}
Siehe: Abschnitt ??
Die Zenerspannung der Diode beträgt \(U_\mathrm {D}=6\,\mathrm {V}\) und die Diode darf eine maximale Verlustleistung von \(P_\mathrm {tot}=\mathrm {400\,mW} \) nicht
überschreiten. Die maximale Eingangsspannung beträgt \( U_0 = \mathrm {12\,V} \).
Wie groß muss der Widerstand \( R \) mindestens sein, damit die Diode nicht zerstört wird?
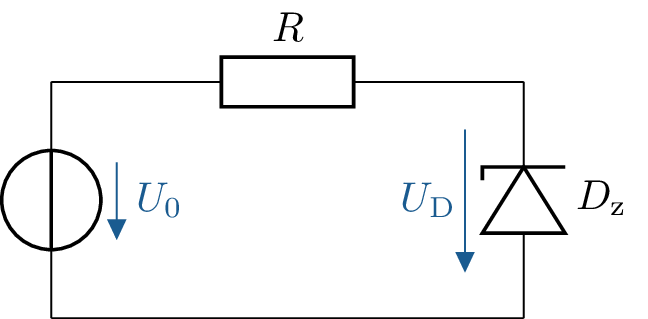
Die Spannung am Widerstand ergibt sich zu: \begin {align*} U_\mathrm {R} &= U_0 - U_\mathrm {D} = \mathrm {12\,V} - \mathrm {6\,V} = \mathrm {6\,V} \end {align*}
Die maximale Verlustleistung der Diode ist: \begin {align*} P_\mathrm {tot} &= U_\mathrm {D} \cdot I = \mathrm {400\,mW} \end {align*}
Daraus folgt der maximale Strom durch die Diode: \begin {align*} I &= \frac {\mathrm {400\,mW}}{\mathrm {6\,V}} = \mathrm {66{,}7\,mA} \end {align*}
Um diesen Strom nicht zu überschreiten, ergibt sich der Mindestwert für den Widerstand: \begin {align*} R &= \frac {U_\mathrm {R}}{I} = \frac {\mathrm {6\,V}}{\mathrm {66{,}7\,mA}} \approx \mathrm {90\,\Omega } \end {align*}
Siehe: Abschnitt ??
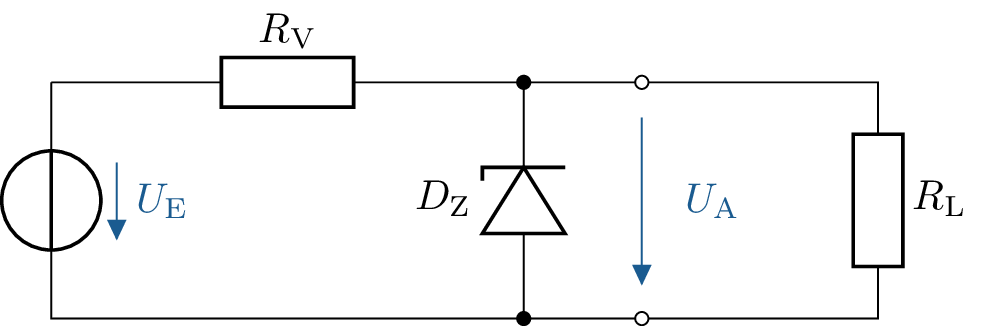
Mit Hilfe einer Zenerdiode soll ein Lastwiderstand \( R_\mathrm {L} = \mathrm {160\,\Omega } \) mit einer stabilisierten Spannung von \( U_\mathrm {A} = \mathrm {8\,V} \) versorgt werden.
Dem Datenblatt der Zenderdiode ist zu entnehmen, dass bei einer Zenerspannung von \( \mathrm {-8\,V} \) ein Zenerstrom von \( \mathrm {-0{,}45\,A} \)
fließt.
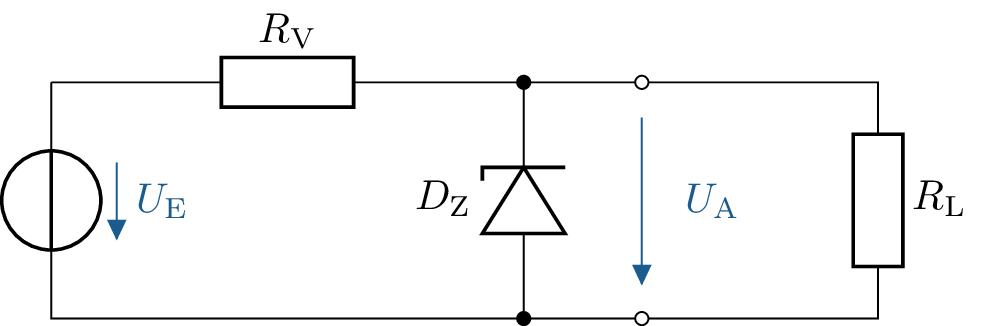
Berechnen Sie den Vorwiderstand \( R_\mathrm {V} \), sodass sich bei einer Eingangsspannung von \( U_\mathrm {E} = \mathrm {10\,V} \) eine Ausgangsspannung von \( U_\mathrm {A} = \mathrm {8\,V} \) einstellt.
Wie groß sind die Leistungen, die an \( R_\mathrm {V} \), \( R_\mathrm {L} \) und an der Diode \( D_\mathrm {Z} \) umgesetzt werden?
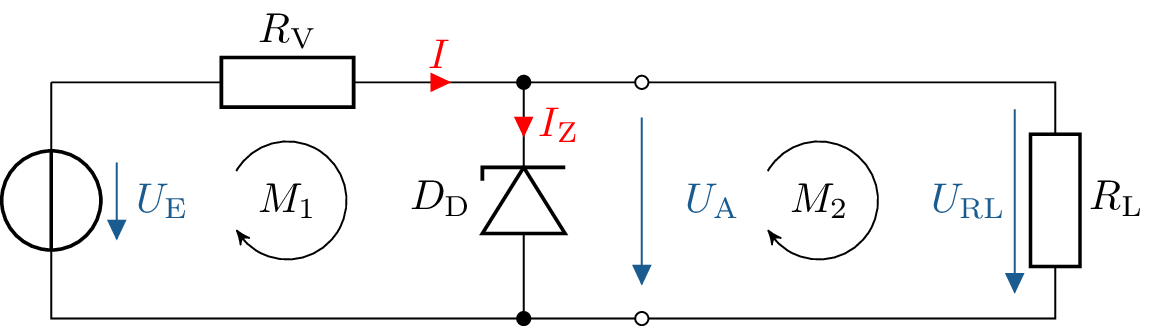
\begin {gather*} I_\mathrm {RL} = \frac {\mathrm {8\,V}}{\mathrm {160\,\Omega }} = \mathrm {0{,}05\,A} \\ I = \mathrm {0{,}05\,A} + \mathrm {0{,}45\,A} = \mathrm {0{,}5\,A} \\ U_\mathrm {RV} = \mathrm {10\,V} - \mathrm {8\,V} = \mathrm {2\,V} \\ R_\mathrm {V} = \frac {\mathrm {2\,V}}{\mathrm {0,5\,A}} = \mathrm {4\,\Omega } \end {gather*}
\begin {gather*} P_\mathrm {RV} = \mathrm {2\,V} \cdot \mathrm {0{,}5\,A} = \mathrm {1\,W} \\ P_\mathrm {RL} = \mathrm {8\,V} \cdot \mathrm {0{,}05\,A} = \mathrm {0{,}4\,W} \\ P_\mathrm {DZ} = \mathrm {8\,V} \cdot \mathrm {0{,}45\,A} = \mathrm {3{,}6\,W} \end {gather*}
Siehe: Abschnitt ??
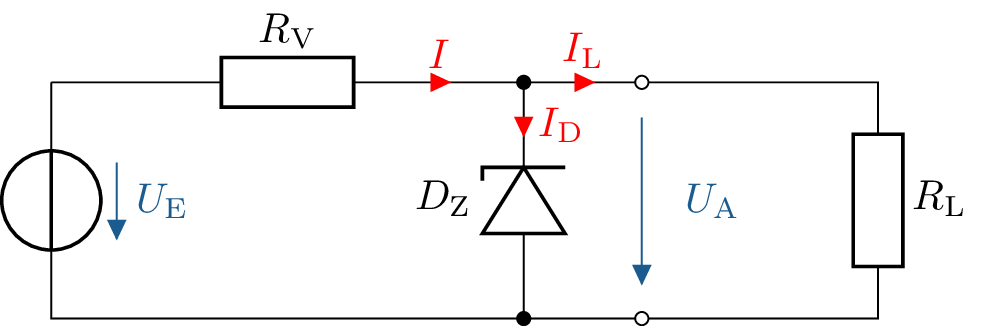
Gegeben ist die folgende Schaltung mit einer Zenerdiode und zwei Widerständen. Die eingesetzte
Zenerdiode besitzt eine Zenerspannung von \( U_\mathrm {Z} = \mathrm {8\,V} \). Die maximale Verlustleistung der Diode beträgt \( P_\mathrm {tot}=\mathrm {8\,W} \). Die Diode
arbeitet im stabilisierenden Bereich, wenn der Strom durch sie mindestens \( \mathrm {5\,mA} \) beträgt. Zusätzlich sind die
folgenden Werte gegeben: \(U_\mathrm {E}=20\,\mathrm {V}\pm 10\%\) und \(R_\mathrm {V} = 10\,\Omega \).
Welchen minimalen und maximalen Widerstandswert darf der Lastwiderstand \( R_\mathrm {L} \) nicht unter- bzw.
überschreiten, damit die Diode einerseits im stabilisierenden Bereich arbeitet und andererseits nicht
überlastet wird?
Gegeben sind: \begin {equation*} U_\mathrm {max} = \mathrm {22\,V} \text { und } U_\mathrm {min} = \mathrm {18\,V} \end {equation*}
Fall 1: Bei \( U_\mathrm {max} = \mathrm {22\,V} \) \begin {gather*} U_\mathrm {RV} = \mathrm {22\,V} - \mathrm {8\,V} = \mathrm {14\,V} \\ I = \frac {\mathrm {14\,V}}{\mathrm {10\,\Omega }} = \mathrm {1{,}4\,A} \\ I = I_\mathrm {D} + I_\mathrm {L} \\ I_\mathrm {D,\ max} = \frac {\mathrm {8\,W}}{\mathrm {8\,V}} = \mathrm {1\,A} \\ I_\mathrm {L} = \mathrm {1{,}4\,A} - \mathrm {1\,A} = \mathrm {0{,}4\,A} \\ R_\mathrm {L} = \frac {\mathrm {8\,V}}{\mathrm {0{,}4\,A}} = \mathrm {20\,\Omega } \Rightarrow R_\mathrm {L,\ max} = \mathrm {20\,\Omega } \end {gather*}
Fall 2: Bei \( U_\mathrm {min} = \mathrm {18\,V} \) \begin {gather*} U_\mathrm {RV} = \mathrm {18\,V} - \mathrm {8\,V} = \mathrm {10\,V} \\ I = \frac {\mathrm {10\,V}}{\mathrm {10\,\Omega }} = \mathrm {1\,A} \\ I_\mathrm {D,\ min} = \mathrm {5\,mA} \\ I_\mathrm {L} = \mathrm {1\,A} - \mathrm {5\,mA} = \mathrm {0{,}995\,A} \\ R_\mathrm {L} = \frac {\mathrm {8\,V}}{\mathrm {0{,}995\,A}} \approx \mathrm {8\,\Omega } \Rightarrow R_\mathrm {L,\ min} \approx \mathrm {8\,\Omega } \end {gather*}
Siehe: Abschnitt ??
In einer einfachen Schaltung wird eine Diode zur Leistungsreduktion eingesetzt. Der Widerstand \(R_\mathrm {L} = 1\,\mathrm {k\Omega }\) stellt eine Heizlast dar. Die Netzspannung beträgt \(230\,\mathrm {V}\) Effektivwert bei einer Frequenz von \(50\,\mathrm {Hz}\).
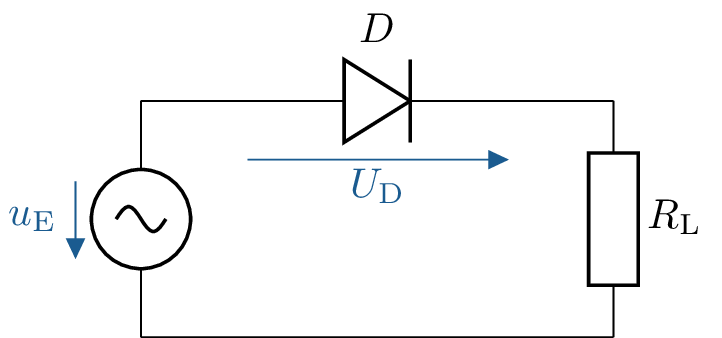
Welche mittlere Leistung wird in \(R_\mathrm {L}\) und in der Diode umgesetzt, wenn die Diode als idealer Gleichtrichter wirkt (d.h. nur eine Halbwelle durchlässt)?
Wie groß wäre die mittlere Leistung bei überbrückter Diode (volle Netzspannung an \(R_\mathrm {L}\))?
Bei einem idealen Ventil: Nach dem Erreichen der Flussspannung verhält sich die Diode wie ein
perfekter Leiter ohne Widerstand.
Da nur eine Halbwelle der Wechselspannung durchgelassen wird, halbiert sich die Leistung im
Lastwiderstand. Die Diode selbst setzt keine Leistung um: \begin {align*} P_\mathrm {D} &= 0\,\mathrm {W} \end {align*}
Die mittlere Leistung im Lastwiderstand beträgt: \begin {align*} P_\mathrm {RL} &= \frac {1}{2} \cdot \frac {(U_\mathrm {eff})^2}{R_\mathrm {L}} = \frac {1}{2} \cdot \frac {(230\,\mathrm {V})^2}{1\,\mathrm {k\Omega }} = 26,45\,\mathrm {W} \end {align*}
Bei überbrückter Diode liegt die volle Wechselspannung am Lastwiderstand an: \begin {align*} P_\mathrm {RL} &= \frac {U_\mathrm {eff}^2}{R_\mathrm {L}} = \frac {230\,\mathrm {V}^2}{1\,\mathrm {k\Omega }} = 52,9\,\mathrm {W} \end {align*}
Siehe: Abschnitt ??
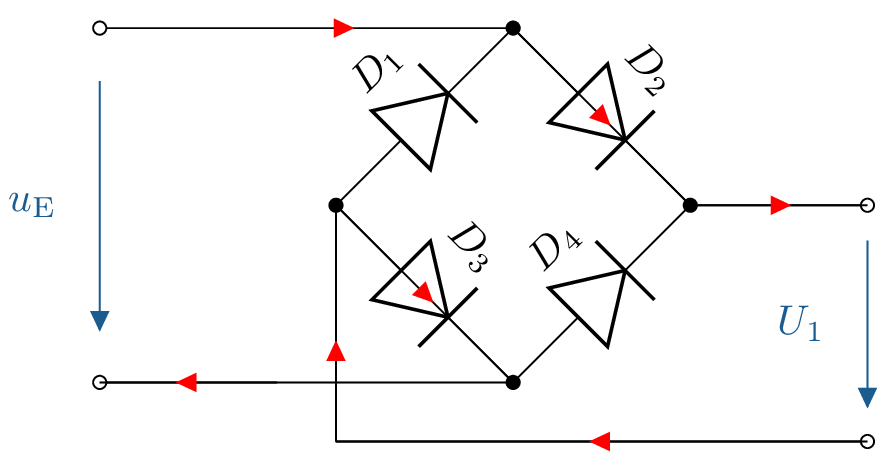
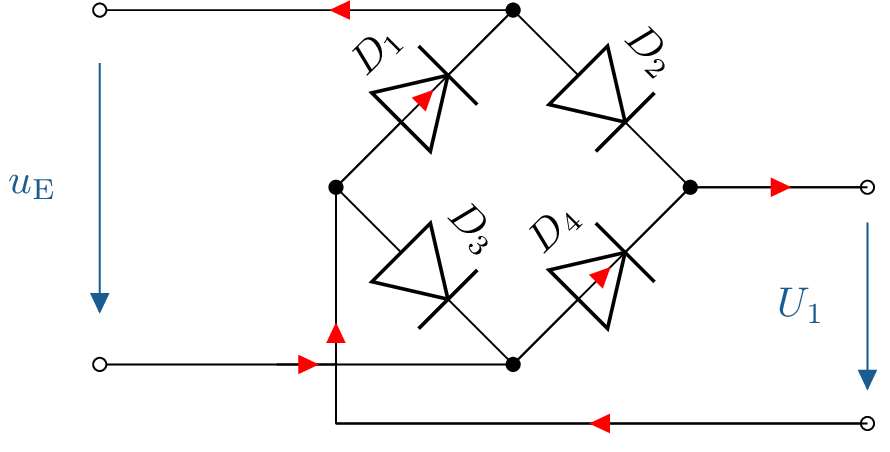
Skizzieren Sie die Spannung \(U_1\) der gegebenen Schaltung. Beachten Sie, dass es sich bei \(u_\mathrm {E}\) um eine Wechselspannung handelt.
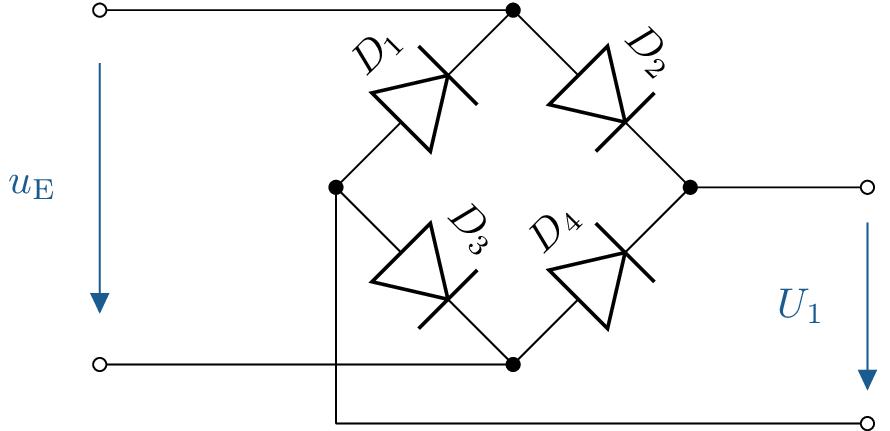
Bei einer negativen Halbwelle fließt der Strom über \(D_{\text {2}}\) und \(D_{\text {3}}\).
Bei einer positiven Halbwelle fließt der Strom über \(D_{\text {4}}\) und \(D_{\text {1}}\).
Siehe: Abschnitt ??
Wie bei allen Dioden muss auch bei Leuchtdioden (LEDs) der Strom begrenzt werden. Dazu wird ein
Vorwiderstand in Reihe geschaltet, wie in der unten gezeigten Schaltung.
Die eingesetzte LED besitzt eine Durchlassspannung von \(U_\mathrm {D} = 2,2\,\mathrm {V}\). Die ideale Helligkeit wird bei einem Strom von \(I_\mathrm {D} = 30\,\mathrm {mA}\)
erreicht. Die Eingangsspannung beträgt \(U_\mathrm {0} = 5\,\mathrm {V}\).
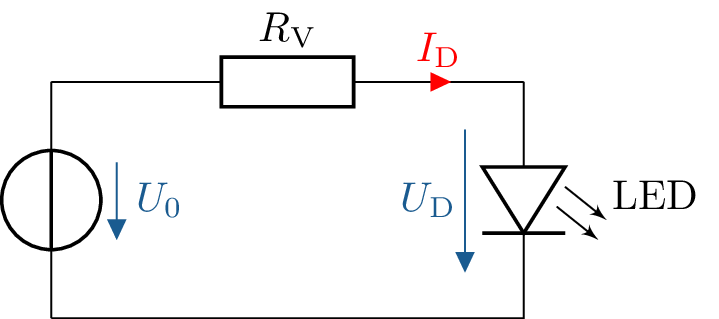
Welchen der folgenden Widerstandswerte würden Sie für \(R\) verwenden, um die LED möglichst nahe an ihrem
optimalen Betriebspunkt (d.h. mit optimaler Helligkeit) zu betreiben?
\(15\,\Omega \), \(33\,\Omega \), \(68\,\Omega \), \(150\,\Omega \), \(180\,\Omega \)
Berechnung der Spannung am Vorwiderstand: \begin {equation*} U_\mathrm {V} = U_\mathrm {0} - U_\mathrm {D} = 5\,\mathrm {V} - 2,2\,\mathrm {V} = 2,8\,\mathrm {V} \end {equation*}
Berechnung des optimalen Vorwiderstands für \( I_\mathrm {D} = \mathrm {30\,mA} \): \begin {equation*} R_\mathrm {V} = \frac {U_\mathrm {V}}{I_\mathrm {D}} = \frac {2,8\,\mathrm {V}}{30\,\mathrm {mA}} = 93,3\,\Omega \end {equation*}
Berechnung des Stroms bei Auswahl eines konkreten Widerstandswertes: \begin {equation*} I_\mathrm {D} = \frac {U_\mathrm {V}}{R} = \frac {2,8\,\mathrm {V}}{150\,\Omega } = 18,7\,\mathrm {mA} \end {equation*}
Berechnung bei zwei Widerständen in Parallelschaltung mit zusätzlichem Serienwiderstand: \begin {gather*} R_\mathrm {ges} = \frac {150\,\Omega \cdot 180\,\Omega }{150\,\Omega + 180\,\Omega } + 15\,\Omega = 96,8\,\Omega \\ I_\mathrm {D} = \frac {2,8\,\mathrm {V}}{96,8\,\Omega } =28,9\,\mathrm {mA} \end {gather*}
Alternative Reihenschaltung: \begin {equation*} R_\mathrm {ges} = 4 \cdot 15\,\Omega + 33\,\Omega = 93\,\Omega \end {equation*}
Fazit: Ein kombinierter Widerstand aus \(4 \cdot 15\,\Omega + 33\,\Omega = 93\,\Omega \) oder eine Parallelschaltung mit \(150\,\Omega \,\|\, 180\,\Omega + 15\,\Omega = 96,8\,\Omega \) führt zu einem Strom nahe dem
optimalen Wert von \(30\,\mathrm {mA}\).
Empfohlene Wahl: Kombination mit Gesamtwiderstand nahe \(93\,\Omega \).
Siehe: Abschnitt ??
Was für ein Bauelement wird mit folgendem Symbol gekennzeichnet?
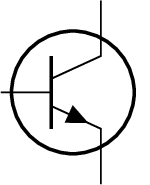
Beim dargestellten Bauelement handelt es sich um einen npn-Transistor. Siehe: Abschnitt ??
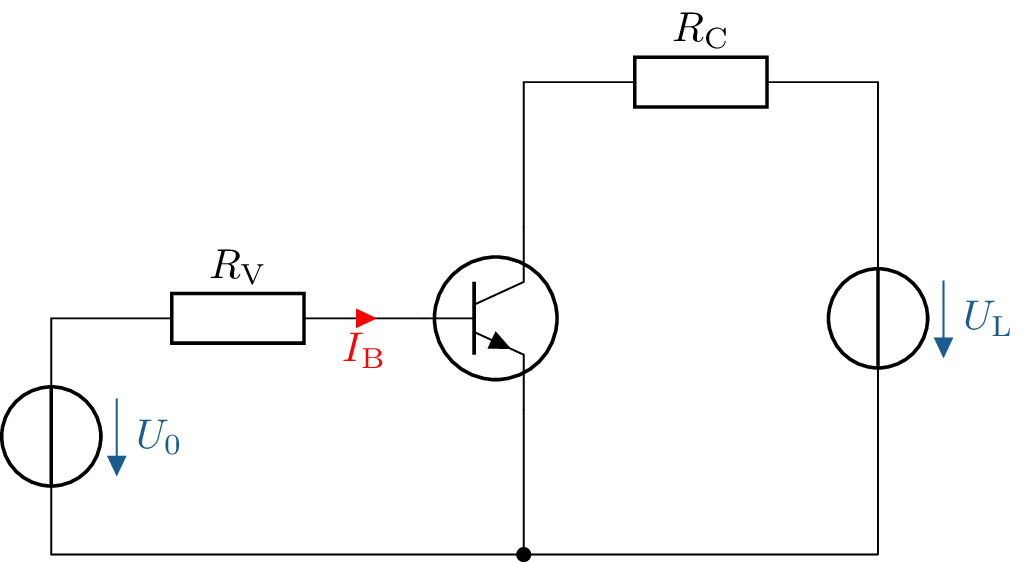
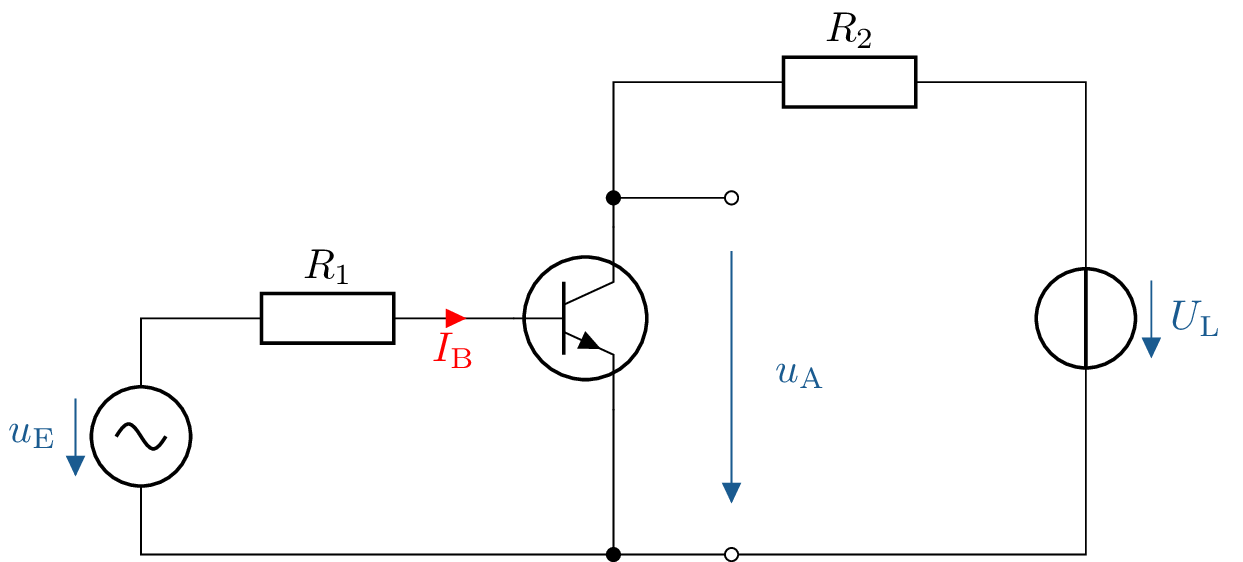
Gegeben ist die abgebildete Transistorschaltung mit den folgenden Parametern: \(U_0=\mathrm {5\,V}\) , \(U_L=\mathrm {15\,V}\), \(R_\mathrm {V}=\mathrm {100\,k\Omega }\) und \(R_\mathrm {V}=\mathrm {500\,\Omega }\).
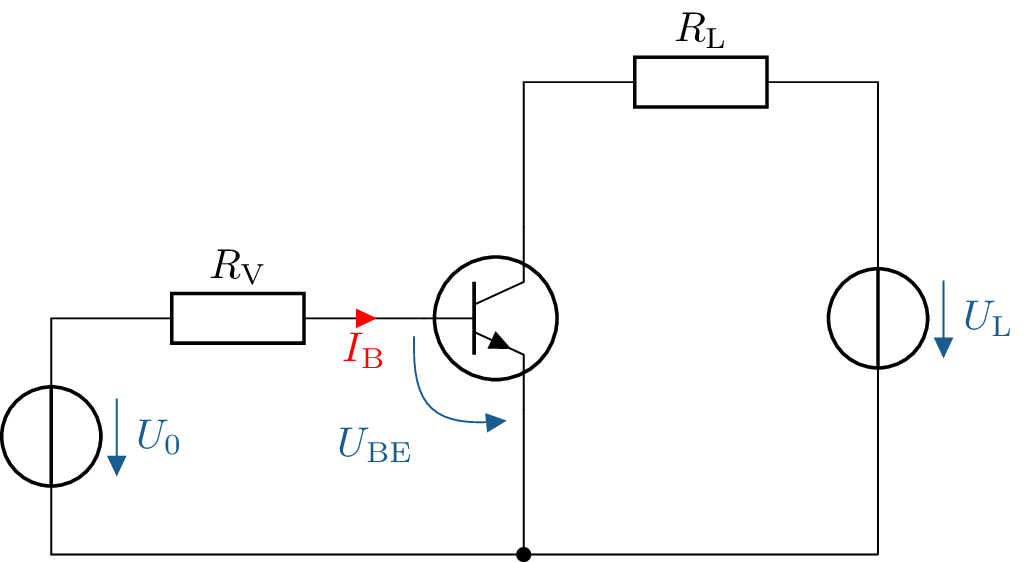
Wie groß ist die Spannung \(U_\mathrm {BE}\) näherungsweise, wenn es sich um einen Siliziumtransistor handelt?
Wie groß ist der Strom \(I_\mathrm {B}\)?
Diese Spannung ist eine materialbedingte Eigenschaft des Silizium-Transistors und bleibt nahezu konstant, unabhängig von der Basisspannung \( U_\text {B} \). Ein npn-Transistor hat im leitenden Zustand eine typische Basis-Emitter-Spannung von: \begin {equation*} U_\text {BE} \approx 0,6\,\text {V} \text { bis } 0,7\,\text {V} \end {equation*}
Obwohl \( U_\text {0} = 5\,\text {V} \) ist, begrenzt der Transistor die Spannung \( U_{BE} \) auf ca. \( 0,6\,\text {V} \), sobald der Transistor leitend ist. Der überschüssige Spannungsabfall wird durch andere Ströme und Bauteile der Schaltung ausgeglichen.
\begin {align*} I_\text {B} = \frac {5\,\text {V} - 0,6\,\text {V}}{100\,\text {k}\Omega } = 44\,\mu \text {A} \end {align*}
Siehe: Abschnitt ?? und ??
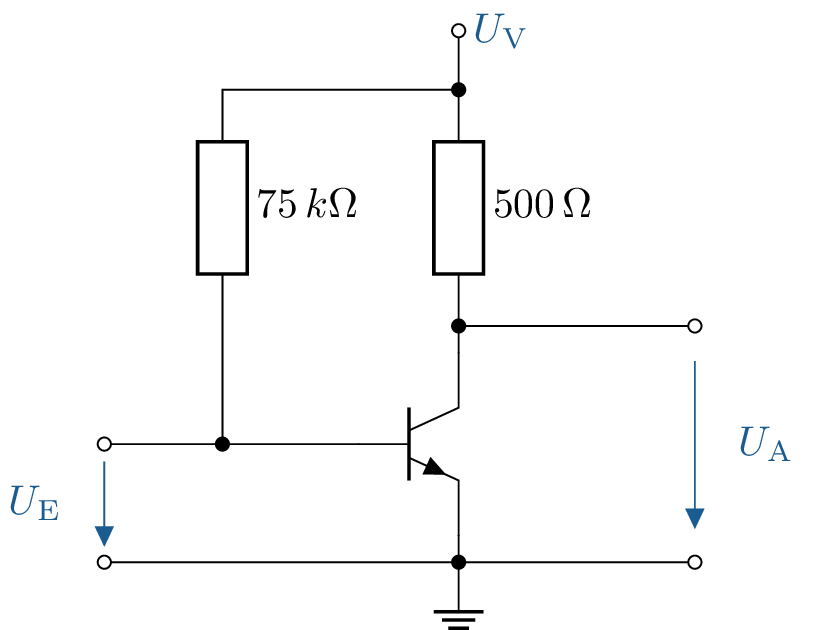
Gegeben ist die abgebildete Transistorschaltung mit den folgenden Parametern: \(U_0=\mathrm {5\,V}\) , \(U_\mathrm {R1}=\mathrm {0,6\,V}\), \(U_\mathrm {L}=\mathrm {15\,V}\), \(R_\mathrm {1}=\mathrm {300\,\Omega }\), \(R_\mathrm {2}=\mathrm {2\,k\Omega }\) und \(R_\mathrm {V}=\mathrm {500\,\Omega }\). Damit der gezeichnete Siliziumtransistor schaltet, braucht er einen Basisstrom von \(50 \, \mathrm {\mu A}\) um durchzuschalten.
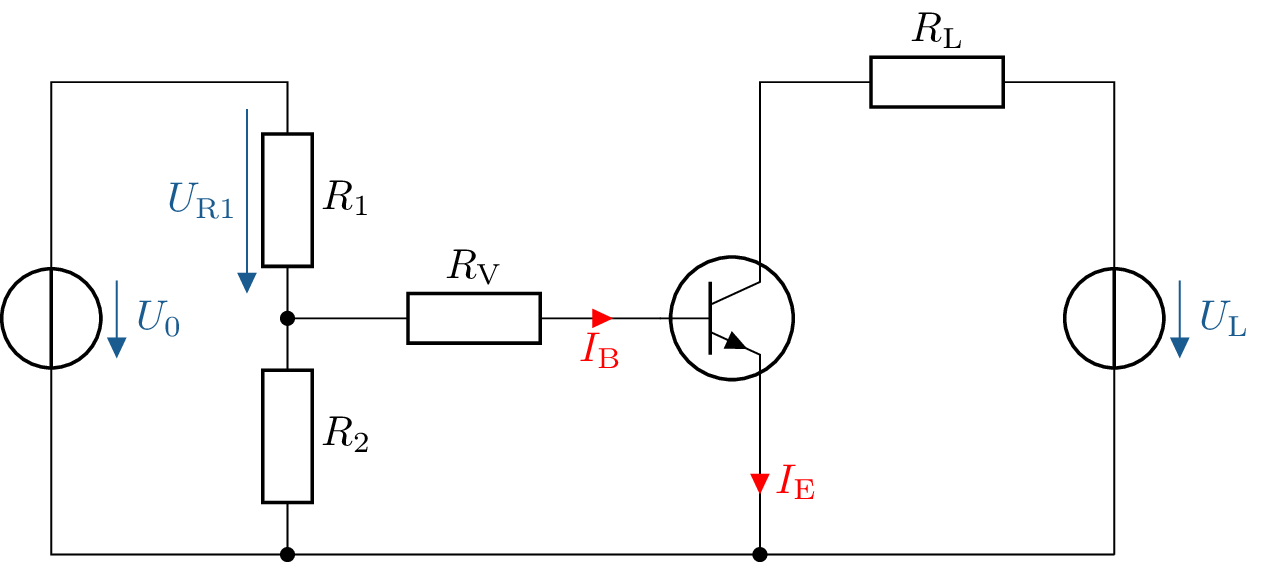
Wie groß muss der Widerstand \(R_\mathrm {V}\) gewählt werden, damit der Transistor durchschaltet?
Angenommen der Spannungsabfall des Transistors \(U_\mathrm {CE}\) beträgt \(7,5 \, \mathrm {V}\), wie groß ist der Strom durch \(I_\mathrm {E}\)?
\[ \frac {5\,\text {V}}{2\,\text {k}\Omega + 0,3\,\text {k}\Omega } = \frac {U_1}{300\,\Omega } \Rightarrow U_\text {1} = 300\,\Omega \cdot \frac {5\,\text {V}}{2\,\text {k}\Omega + 0,3\,\text {k}\Omega } = 0,65\,\text {V} \] \[ 5\,\text {V} = 0,65\, \text {V} + U_\text {RV} + 0,6\,\text {V} \] \[ U_\text {RV} = 5\,\text {V} - 0,65\,\text {V} - 0,6\,\text {V} = 3,75\,\text {V} \] \[ R_\text {V} = \frac {3,75\,\text {V}}{50\,\mu \text {A}} = 75\,\text {k}\Omega \]
\[ I_\text {C} = \frac {15\,\text {V} - 7,5\,\text {V}}{500\,\Omega } = 15\,\text {mA} \] \[ I_\text {E} = I_\text {C} + I_\text {B} = 15\,\text {mA} + 50\,\mu \text {A} = 15,05\,\text {mA} \] \[ \frac {I_\text {C}}{I_\text {B}} = \beta = 300 \]
Siehe: Abschnitt ?? und ??
Gegeben ist die abgebildete Transistorschaltung mit den folgenden Parametern: \(U_0=\mathrm {5\,V}\) und \(U_L=\mathrm {15\,V}\). Damit der gezeigte Siliziumtransistor schaltet, benötigt er einen Basisstrom von \( I_\mathrm {B}=\mathrm {50\,\mu A} \), um in den leitenden Zustand zu gelangen.
Wie groß muss der Vorwiderstand \( R_\mathrm {V} \) gewählt werden, damit der Transistor durchschaltet?
Der Transistor hat einen Stromverstärkungsfaktor \( \beta = 180 \) und einen Kollektorwiderstand \( R_\mathrm {C} = \mathrm {200\,\Omega } \). Wie groß sind der Kollektorstrom \( I_\mathrm {C} \) und der Spannungsabfall zwischen Kollektor und Emitter \( U_\mathrm {CE} \)?
Berechnung des Vorwiderstands für den Basisstrom: \begin {equation*} R_\mathrm {V} = \frac {U}{I} = \frac {\mathrm {5\,V} - \mathrm {0{,}6\,V}}{\mathrm {50\,\mu A}} = \frac {\mathrm {4{,}4\,V}}{\mathrm {50\,\mu A}} = \mathrm {88\,k\Omega } \end {equation*}
Berechnung des Kollektorstroms mit Stromverstärkungsfaktor: \begin {gather*} \beta = \frac {I_\mathrm {C}}{I_\mathrm {B}} \\ I_\mathrm {C} = \beta \cdot I_\mathrm {B} = 180 \cdot \mathrm {50\,\mu A} = \mathrm {9\,mA} \end {gather*}
Berechnung des Spannungsabfalls am Kollektorwiderstand: \begin {equation*} U_\mathrm {RC} = I_\mathrm {C} \cdot R_\mathrm {C} = \mathrm {9\,mA} \cdot \mathrm {200\,\Omega } = \mathrm {1{,}8\,V} \end {equation*}
Berechnung der Spannung zwischen Kollektor und Emitter: \begin {equation*} U_\mathrm {CE} = \mathrm {15\,V} - \mathrm {1{,}8\,V} = \mathrm {13{,}2\,V} \end {equation*}
Siehe: Abschnitt ?? und ??
Mithilfe eines Bipolartransistor soll eine LED betrieben werden. Dabei muss durch die LED ein Strom von \(I_\mathrm {D}=30\,\mathrm {mA}\)
fließen, damit sie ihre optimale Leuchtkraft erreicht.
Der verwendete Transistor besitzt einen Stromverstärkungsfaktor von \(\beta = 50\) und im durchgeschalteten Zustand
eine Kollektor-Emitter-Spannung von \(U_\mathrm {CE} = 0,3\,\mathrm {V}\). Zusätzlich sind die folgenden Parameter gegeben: \(R_1=3,3\,\mathrm {k\Omega }\), \(R_2=270\,\mathrm {\Omega }\) und
\(U_\mathrm {L}=9\,\mathrm {V}\).
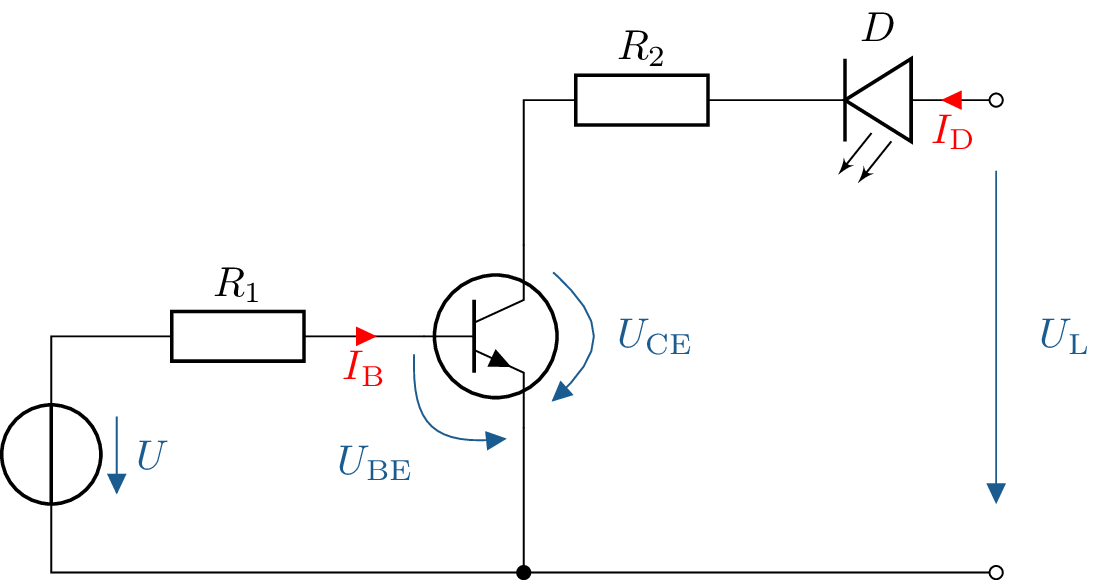
Welche Spannung \(U\) muss an der Basis anliegen, damit der Transistor durchschaltet?
Berechnung des Kollektorstroms bei bekannter Spannung und Lastwiderstand: \begin {align*} I_\mathrm {C} & = \frac {U}{R}\\ I_\mathrm {C} & = \frac {9\,\mathrm {V} - 0,3\,\mathrm {V}}{270\,\Omega } = 32,2\,\mathrm {mA} \end {align*}
Berechnung des benötigten Basisstroms mit dem Stromverstärkungsfaktor \(\beta = 50\): \begin {align*} I_\mathrm {B} & = \frac {I_\mathrm {C}}{\beta }\\ I_\mathrm {B} & = \frac {32,2\,\mathrm {mA}}{50} = 0,644\,\mathrm {mA} \end {align*}
Spannungsabfall am Vorwiderstand: \begin {align*} U_\mathrm {V} = 0,644\,\mathrm {mA} \cdot 3,3\,\mathrm {k\Omega } = 2,12\,\mathrm {V} \end {align*}
Gesamte Basisspannung (inkl. \( U_\mathrm {BE} \)): \begin {align*} U = U_\mathrm {V} + U_\mathrm {BE} = 2,12\,\mathrm {V} + 0,6\,\mathrm {V} = 2,72\,\mathrm {V} \end {align*}
Antwort: Die Basisspannung muss \( 2{,}72\,\mathrm {V} \) betragen, damit der Transistor durchschaltet.
Siehe: Abschnitt ?? und ??
Der Stromverstärkungsfaktor des verwendeten Siliziumtransistors beträgt \( \beta = 150\) und die Versorgungsspannung liegt bei \(U_\mathrm {V} = 15\,\mathrm {V}\). Die Schaltung soll so dimensioniert werden, dass der Kollektorstrom \(I_\mathrm {C} = 2\,\mathrm {mA}\) beträgt.
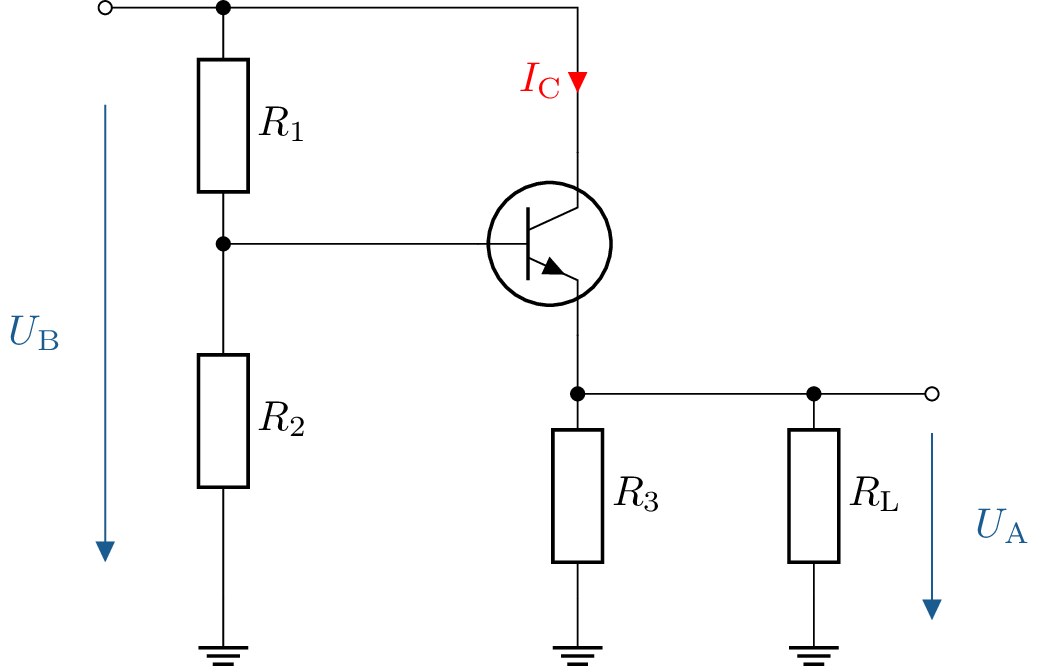
Dimensionieren Sie den Widerstand \(R_3\) so, dass bei einer Spannung am Ausgang von \(U_\mathrm {A}=3\,\mathrm {V}\) der Strom durch \(R_3\) genau \(75\%\) des Emitterstroms beträgt.
Bestimmen Sie die Widerstände \(R_1\) und \(R_2\), unter der Annahme, dass die Kollektor-Basis-Spannung \(U_\mathrm {BE} = 0,6\,\mathrm {V}\) beträgt und durch \(R_2\) etwa das 9-fache des Basisstroms \(I_\mathrm {B}\) fließt.
Berechnung des Basisstroms über den Stromverstärkungsfaktor: \begin {gather*} I_\mathrm {B} = \frac {I_\mathrm {C}}{\beta } = \frac {\mathrm {2\,mA}}{150} = \mathrm {13,3\,\mu A} \\ I_\mathrm {E} = I_\mathrm {C} + I_\mathrm {B} = \mathrm {2\,mA} + \mathrm {13,3\,\mu A} = \mathrm {2,013\,mA} \\ I_\mathrm {R_3} = 0,75 \cdot I_\mathrm {E} = 0,75 \cdot \mathrm {2{,}013\,mA} = \mathrm {1,51\,mA} \\ R_3 = \frac {\mathrm {3\,V}}{\mathrm {1,51\,mA}} = \mathrm {1,99\,k\Omega } \end {gather*}
Berechnung des Stroms durch \( R_2 \): \begin {gather*} I_{R_2} = 9 \cdot I_\mathrm {B} = 9 \cdot \mathrm {13,3\,\mu A} = \mathrm {0,12\,mA} \\ R_2 = \frac {U_\mathrm {a} + U_\mathrm {BE}}{I_\mathrm {R_2}} = \frac {\mathrm {3\,V} + \mathrm {0,6\,V}}{\mathrm {0,12\,mA}} = \mathrm {30\,k\Omega } \end {gather*}
Berechnung des Stroms durch \(R_1\), welcher gleich \(I_\mathrm {R_2}\) ist: \begin {gather*} R_1 = \frac {U_\mathrm {BE}}{I_\mathrm {R_1}} = \frac {0,6\,\mathrm {V}}{0,12\,\mathrm {mA}} = 5,6\,\mathrm {k\Omega } \end {gather*}
Siehe: Abschnitt ??
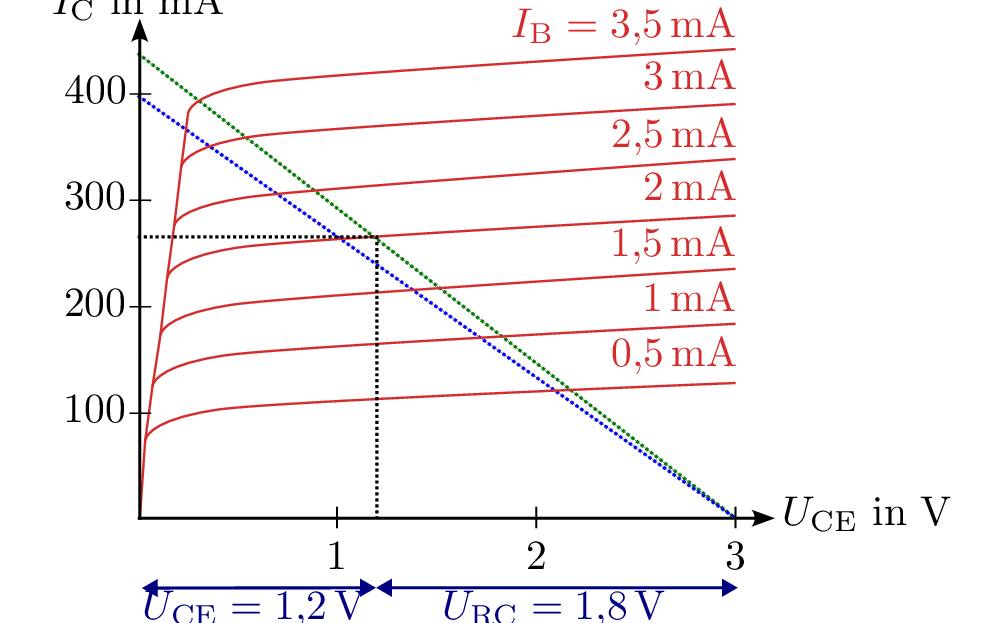
Gegeben ist die folgende Schaltung mit dem Ausgangskennlinienfeld eines Transistors.
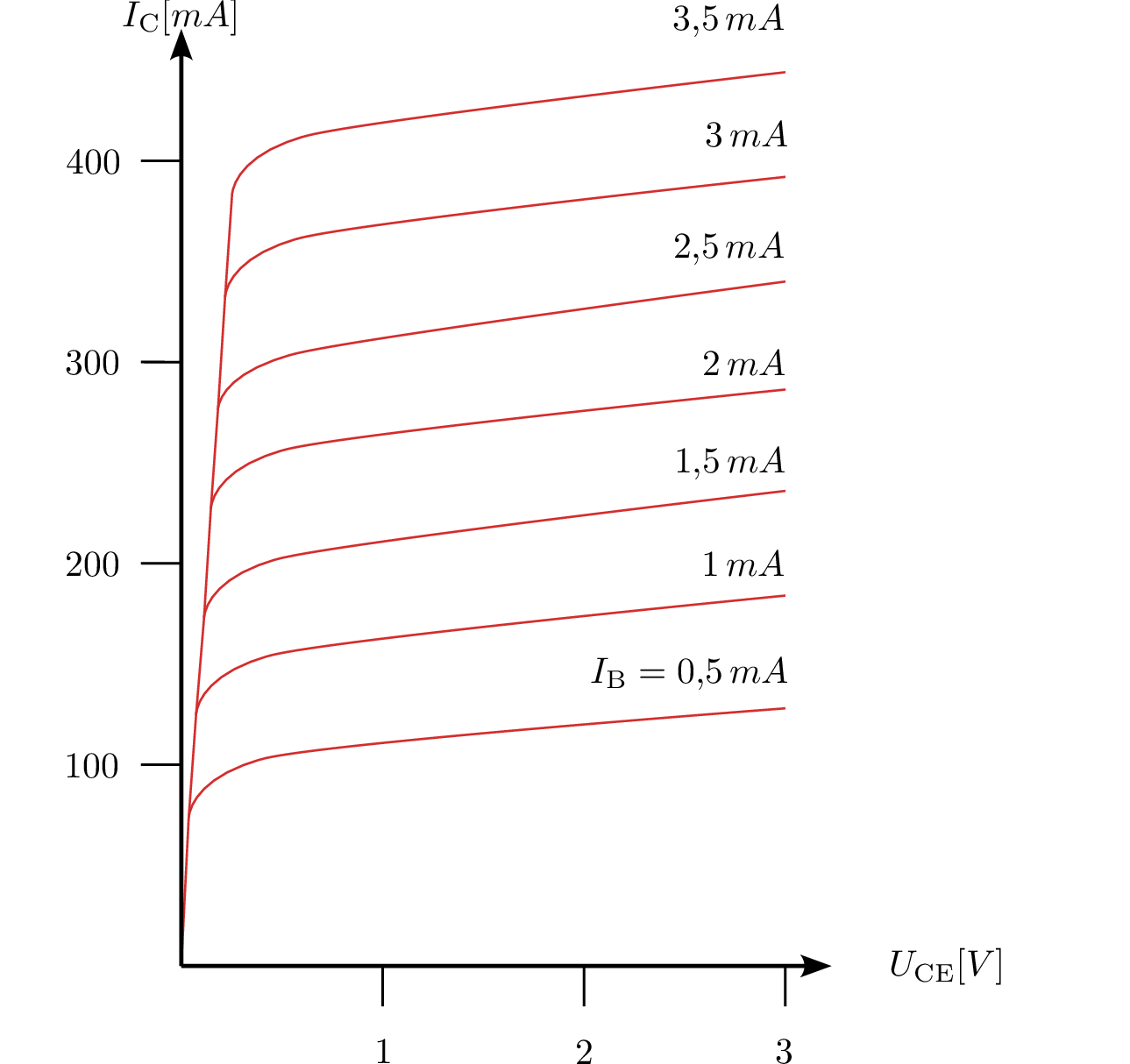
Wie groß ist der maximale Kollektorstrom des idealen Transistors (bei \(R_\mathrm {CE} = 0\,\Omega \)), wenn der Kollektorwiderstand \(R_\mathrm {C} = 7,5\,\Omega \) beträgt und die Versorgungsspannung \(U_\mathrm {V} = 3\,\mathrm {V}\) ist?
Bestimmen Sie \(U_\mathrm {CE}\), \(U_\mathrm {RC}\) und \(I_\mathrm {C}\) des realen Transistors bei einem Basisstrom von \( I_\mathrm {B} = \mathrm {2\,mA} \). Tragen Sie dazu die Widerstandsgerade in das Kennlinienfeld ein.
Für einen neuen Arbeitspunkt fallen nur noch \(1,7\,\mathrm {V}\) über dem Kollektorwiderstand \(R_\mathrm {C}\) ab, der Basisstrom beträgt weiterhin \(2\,\mathrm {mA}\). Bestimmen Sie den neuen Widerstand \(R_\mathrm {C}\).
Berechnung des maximalen Kollektorstroms bei idealem Transistor (\( R_\mathrm {CE} = 0 \)): \begin {equation*} I_\mathrm {C} = \frac {U_\mathrm {V}}{R_\mathrm {C}} = \frac {3\,\mathrm {V}}{7,5\,\Omega } = 400\,\mathrm {mA} \end {equation*}
Bestimmung der Spannungen und des Kollektorstroms laut Kennlinienfeld:
\begin {gather*} U_\mathrm {CE} = 1,2\,\mathrm {V} \\ U_\mathrm {RC} = 1,8\,\mathrm {V} \\ I_\mathrm {C} = \frac {U_\mathrm {RC}}{R_\mathrm {C}} = \frac {1,8\,\mathrm {V}}{7,5\,\Omega } = 240\,\mathrm {mA} \end {gather*}
Berechnung des neuen Widerstandswerts bei gleichem \(I_\mathrm {C}\) und neuer Spannung \(U_\mathrm {RC} = 1,7\,\mathrm {V}\): \begin {equation*} R_\mathrm {C} = \frac {U_\mathrm {RC}}{I_\mathrm {C}} = \frac {1,7\,\mathrm {V}}{240\,\mathrm {mA}} = 7,08\,\Omega \end {equation*}
Siehe: Abschnitt ??
Gegeben ist die folgende Schaltung mit dem Kennlinienfeld des Transistors. Die Versorgungsspannung
beträgt \( U_\mathrm {V} = \mathrm {6\,V} \). Der Arbeitspunkt liegt bei der halben Betriebsspannung.
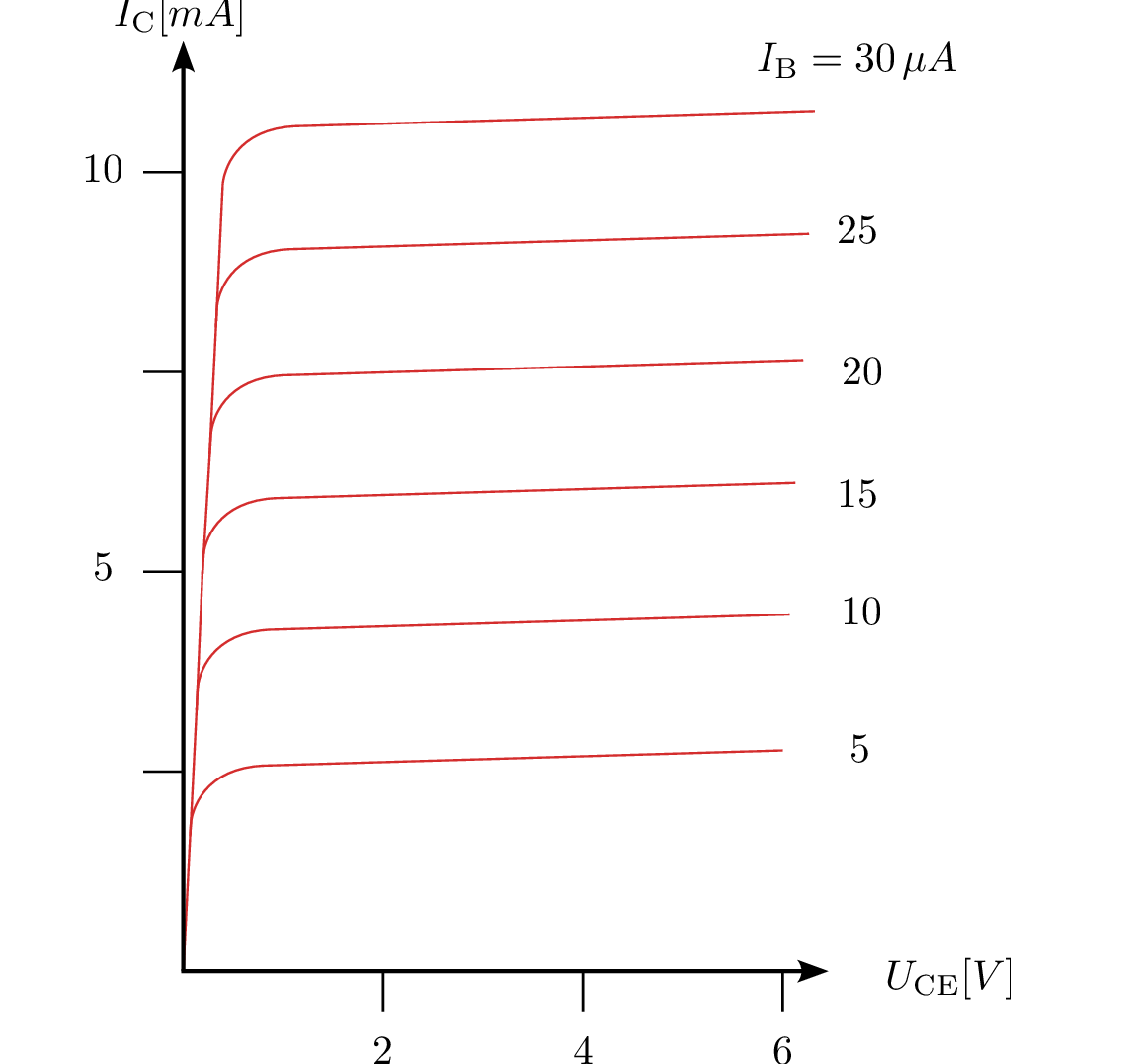
Bestimmen Sie die folgenden Werte aus dem Kennlinienfeld:
Die Paare \( I_\mathrm {B} / U_\mathrm {BE} \) und \( I_\mathrm {C} / U_\mathrm {CE} \) im Arbeitspunkt
Die Stromverstärkung \( \beta \)
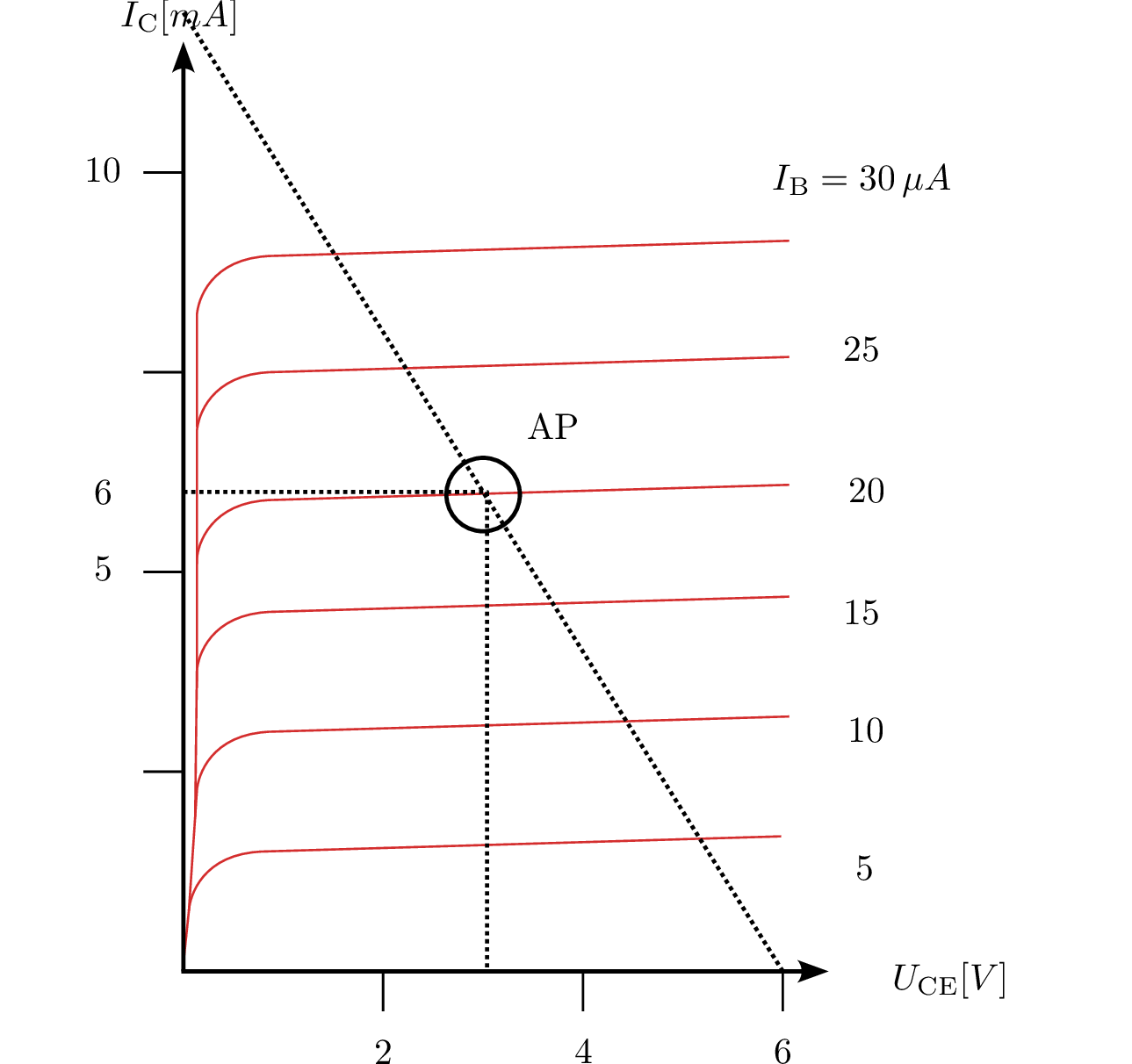
Gegeben sind folgende Werte im Arbeitspunkt: \begin {gather*} U_\mathrm {CC} = \mathrm {6\,V} \\ U_\mathrm {CE} = \mathrm {3\,V} \\ I_\mathrm {C} = \mathrm {6\,mA} \\ U_\mathrm {BE} = \mathrm {0{,}62\,V} \\ I_\mathrm {B} = \mathrm {20\,\mu A} \end {gather*}
Berechnung der Stromverstärkung \( \beta \): \begin {equation*} \beta = \frac {I_\mathrm {C}}{I_\mathrm {B}} = \frac {\mathrm {6\,mA}}{\mathrm {20\,\mu A}} = \mathrm {300} \end {equation*}
Siehe: Abschnitt ??
Was passiert wenn an einen Transistor eine reine Wechselspannung angelegt wird?
Wenn an einen Transistor eine reine Wechselspannung angelegt wird, tritt kein kontinuierlicher Verstärkungsbetrieb auf.
Das führt zu folgenden Effekten:
Verzerrungen im Ausgangssignal, da nur die positiven Halbwellen verstärkt werden.
Die negative Halbwelle wird abgeschnitten, was einer Gleichrichtung des Signals ähnelt.
Es erfolgt keine lineare Verstärkung, da der Transistor zwischen Sperr- und Sättigungszustand wechselt.
Siehe: Abschnitt ??
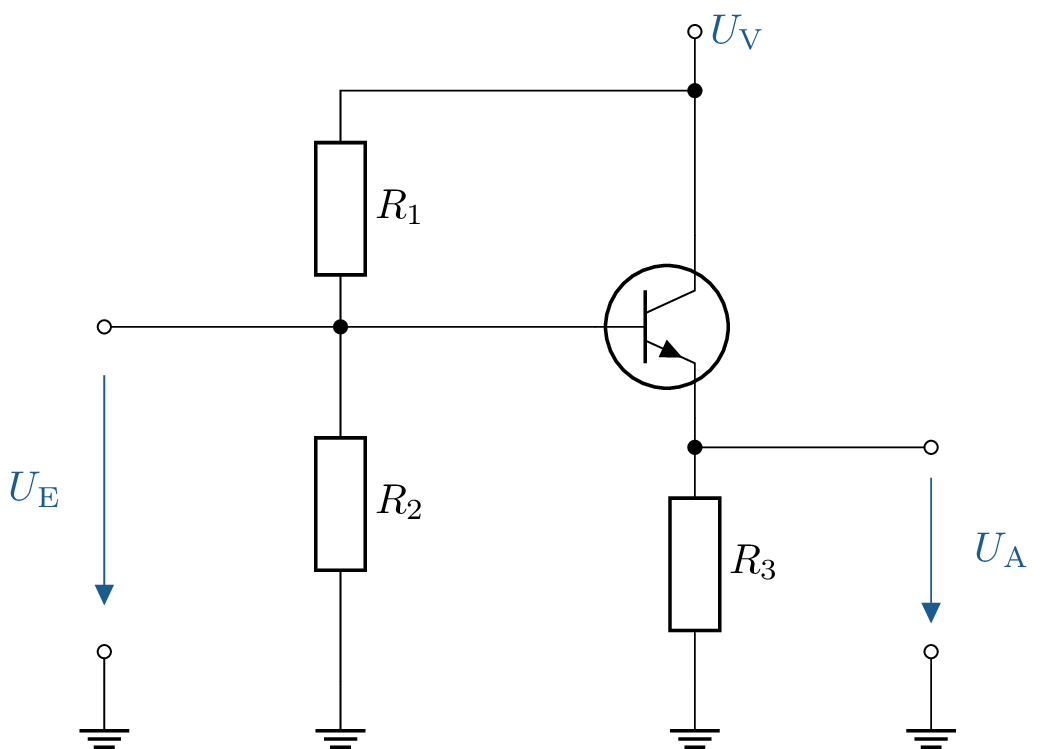
Zeichnen Sie das Kleinsignalersatzschaltbild der gegebenen Schaltung.
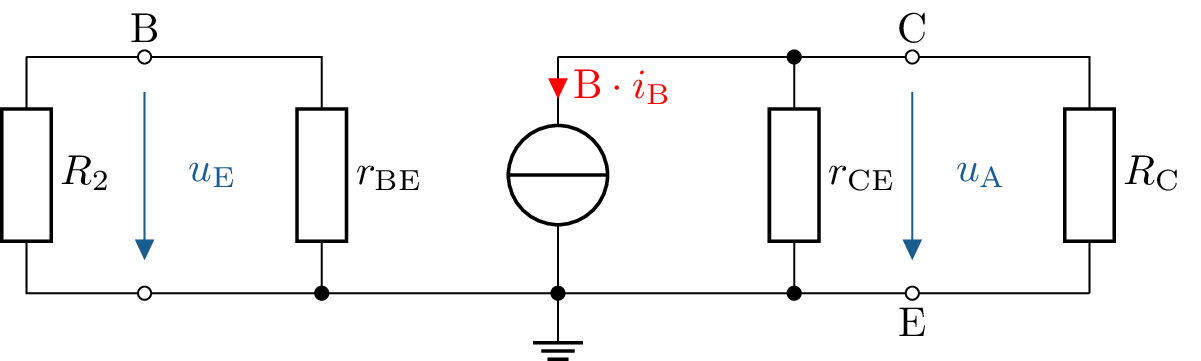
Siehe: Abschnitt ?? und ??.
Zeichnen Sie das Kleinsignalersatzschaltbild der gegebenen Schaltung.
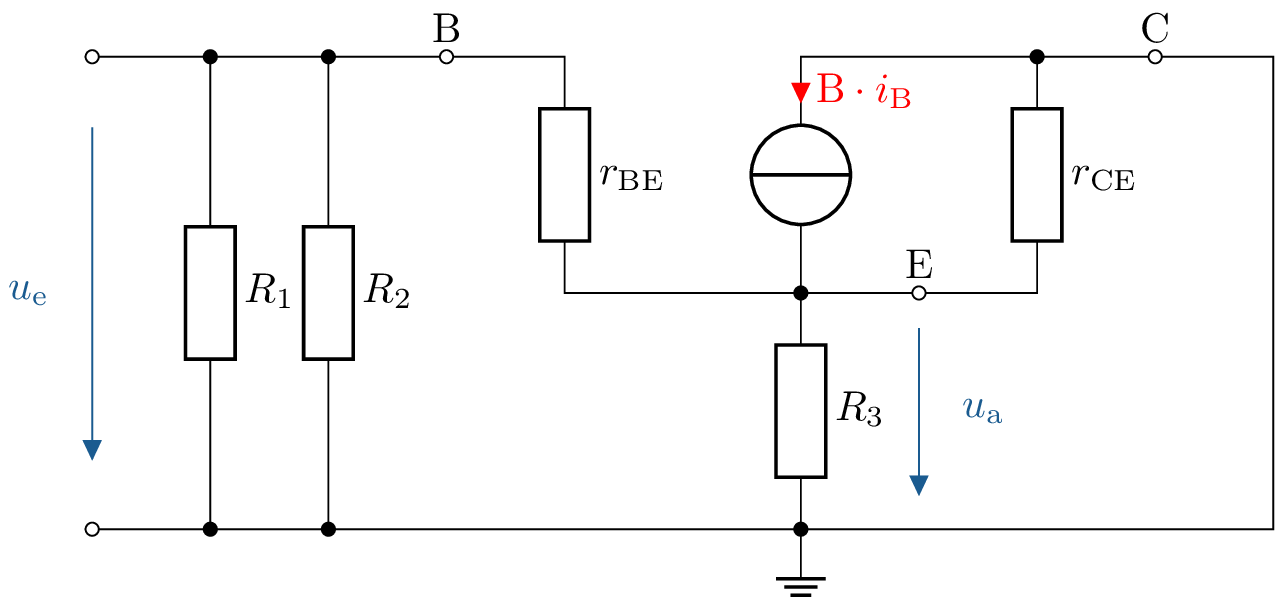
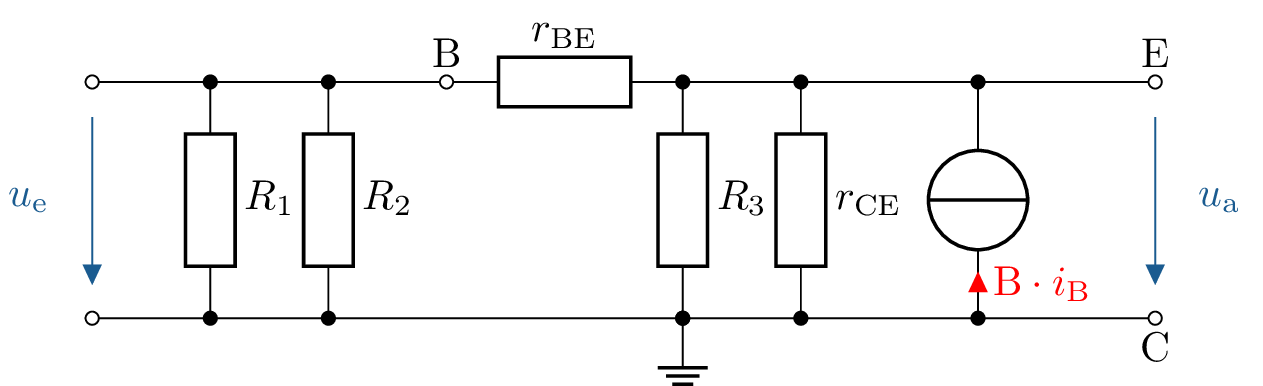
Siehe: Abschnitt ?? und ??.
Bei welcher Spannung an Source-Gate leitet ein Sperrschichttransistor den meisten Strom?
In der Regel beträgt \(U_\mathrm {BE}=0,7\, \mathrm {V}\).
Siehe: Abschnitt ??
Wo fließt bei dem dargestellten Transistor der meiste Strom?
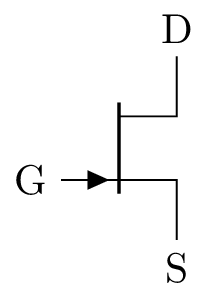
Zwischen Gate und Source.
Siehe: Abschnitt ??
In welche zwei Bereiche lässt sich die Ausgangskennlinie des Sperrschichttransistors unterteilen?
In Sättigungs- und Widerstandsbereich.
Siehe: Abschnitt ??
Ohne das Anlegen einer Spannung ergeben sich die folgenden Verteilungen von p- und n-Gebieten. Um was für einen Typ von Transistor handelt es sich?
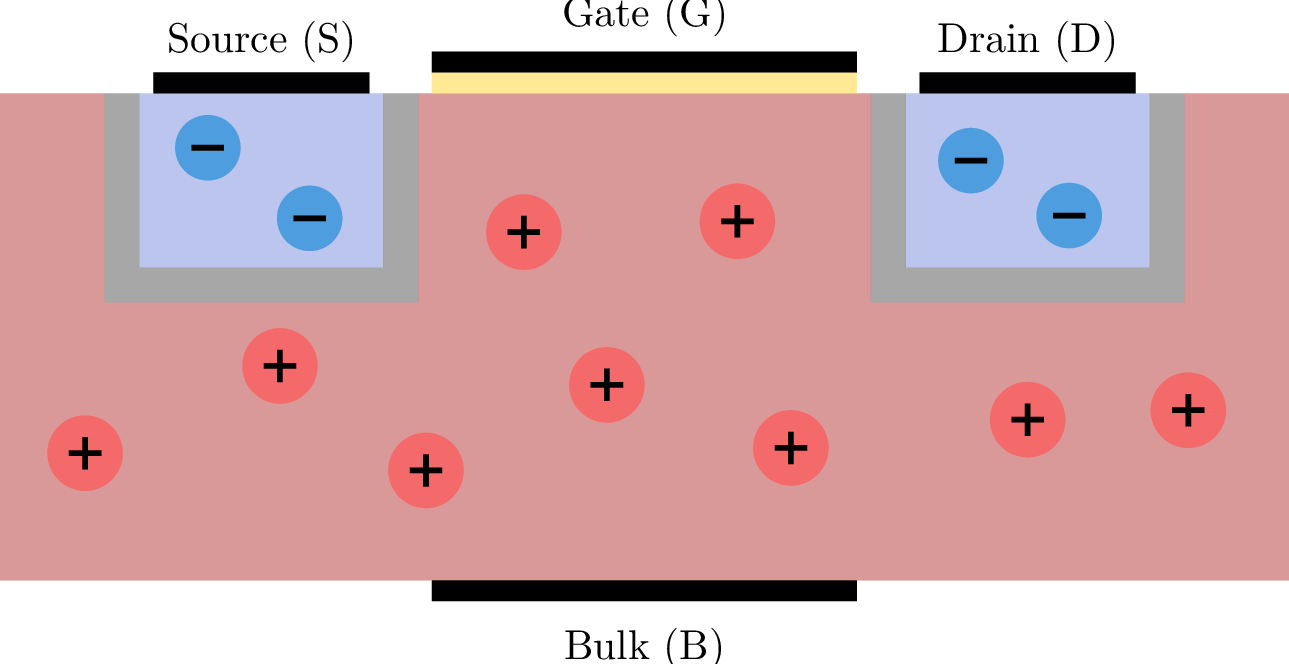
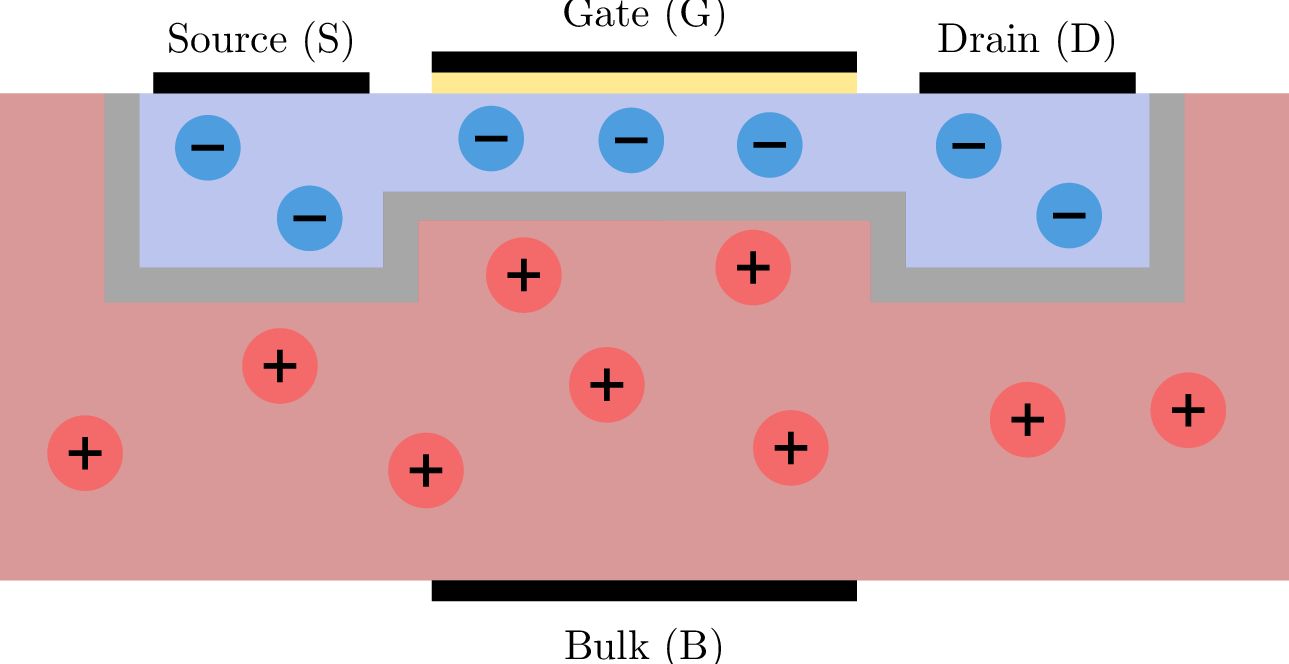
n-Kanal selbstsperrend (Verarmungstyp) Siehe: Abschnitt ??
p-Kanal selbstsperrend (Verarmungstyp) Siehe: Abschnitt ??
n-Kanal selbstleitend (Anreicherungstyp) Siehe: Abschnitt ??
p-Kanal selbstleitend (Anreicherungstyp) Siehe: Abschnitt ??
Was sagt das C in CMOS aus?
Unterscheidung von Anreicherungs- und Verarmungstyp
Die Verwendung von JFETs und MOSFETS in einer Schaltung
Spiegelt den Verlauf der Transferkennlinie wieder
Weißt auf die Spannungsempfindlichkeit von MOSFETs hin
In einer Schaltung werden sowohl p- als auch n-Kanal Transistoren verwendet
In einer Schaltung werden sowohl p- als auch n-Kanal Transistoren verwendet
Siehe: Abschnitt ??
Zwei npn-Bipolartransistoren bilden zusammen einen rauscharmen Verstärker für Signale im Bereich unter \(1\, \mathrm {\mu V}\). Die Versorgungsspannung beträgt \(U_1=10\,\mathrm {V}\). Am Kollektor des Transistors \(\mathrm {T_2}\) liegt eine Spannung von \(4\,\mathrm {V}\) gegenüber Masse an. Im Arbeitspunkt von \(T_1\) und \(T_2\) kann für die Basis-Emitter-Spannungen jeweils \(U_\mathrm {BE}=600\,\mathrm {mV}\) angenommen werden. Die Kollektorströme \(\mathrm {I_{C}}\) sind sehr groß gegenüber den Basisströmen \(I_\mathrm {B}\) anzunehmen, daher gilt näherungsweise \(I_\mathrm {C} = I_\mathrm {E}\). Zusätzlich sind die folgenden Parameter gegeben:
\(R_1 = 10\, \mathrm {k\Omega }\), \(R_2 = 10\, \mathrm {k\Omega }\), \(R_3 = 2\, \mathrm {k\Omega }\), \(R_4 = 300\, \mathrm {k\Omega }\), \(R_5 = 10\, \mathrm {M\Omega }\)
\(C_1 = 1\, \mathrm {\mu F}\), \(C_2 = 1\, \mathrm {\mu F}\)
\(U_1 = 10\, \mathrm {V}\), \(\hat {u}_\mathrm {E} = 0,1\, \mathrm {mV}\)
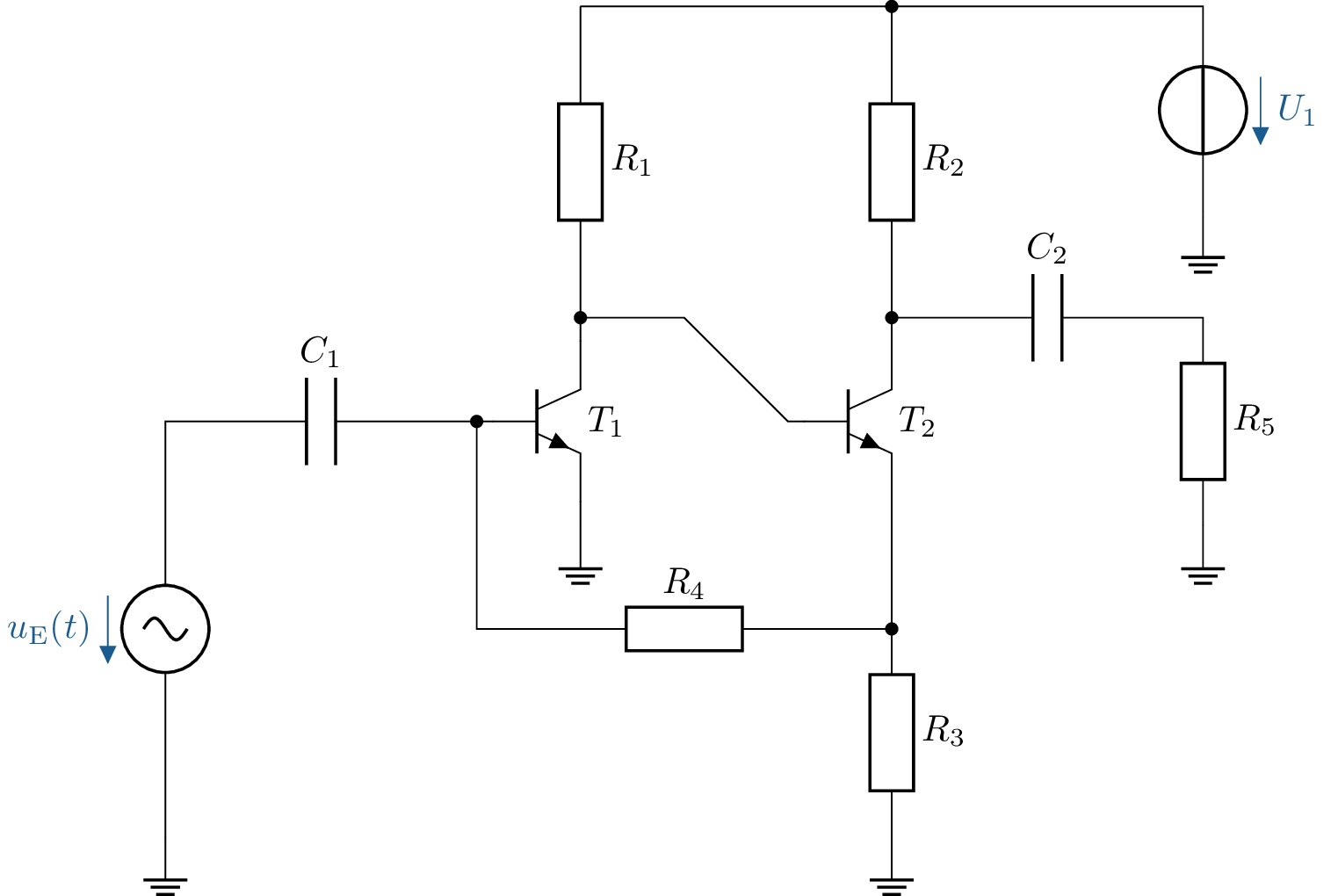
Wie groß ist der maximale Strom durch \(R_2\) im Arbeitspunkt (\(I_\mathrm {R2}=I_\mathrm {C,\,T2}\))?
Wie groß ist der Strom durch \(R_3\) näherungsweise, wenn \(R_4 >> R_3\)?
Wie groß ist die Spannung, die über \(R_3\) abfällt?
Wie groß ist die Gleichspannung an der Basis von \(T_2\) (\(U_\mathrm {B,\,T2}=U_\mathrm {CE,\,T1}\))?
Wie groß ist der Strom durch \(R_1\) (\(I_\mathrm {R1}=I_\mathrm {C,\,T1}\))?
Erläutern Sie die Arbeitspunktstabiliserung der gesamten Schaltung auf Grund der Gegenkopplung über \(R_4\).
Wie groß ist die Steilheit \(S\) von \(T_\mathrm {1}\), wenn zusätzlich \(U_\mathrm {T} = 26\, \mathrm {mV}\) gegeben ist?
Wie groß ist die Spannungsverstärkung \(A_\mathrm {V} = \frac {\Delta U_\mathrm {CE}}{\Delta U_\mathrm {BE}}\), der ersten Transistorstufe?
Wie groß ist die Spannungsverstärkung \(A_\mathrm {V}\) der zweiten Transistorstufe, unter Verwendung der Definition \(A_\mathrm {V,T2}=\frac {\Delta U_\mathrm {C}}{\Delta U_\mathrm {B}}\)? Zur Lösung müssen zusätzlich die Widerstände \(R_2\) und \(R_3\) berücksichtigt werden.
Wie groß ist die Spannungsverstärkung der beiden Stufen \(T_\mathrm {1}\) und \(T_\mathrm {2}\) zusammen?
Zeichnen Sie das Kleinsignal-Ersatzschaltbild der gesamten Schaltung. Ersetzen Sie darin die beiden Transistoren im Arbeitspunkt jeweils durch eine steuerbare Stromquelle \(S=\beta \cdot i_\mathrm {B}\) und einen differentiellen Eingangswiderstand \(r_\mathrm {BE}\).
\begin {align*} I_\mathrm {C} & = \frac {6\,\mathrm {V}}{10\,\mathrm {k\Omega }} = 0,6\,\mathrm {mA} \end {align*}
\begin {align*} I_\mathrm {C,T2} & = 0,6\,\mathrm {mA} \end {align*}
\begin {align*} U_{\mathrm {R3}} & = 0,6\,\mathrm {mA} \cdot 2\,\mathrm {k\Omega } = 1,2\, \mathrm {V} \end {align*}
\begin {align*} 1,2\, \mathrm {V} + 0,6\,\mathrm {V} = 1,8\,\mathrm {V} \end {align*}
\begin {align*} I_\mathrm {C,T1} & = \frac {8,2\,\mathrm {V}}{10\,\mathrm {k\Omega }} = 0,82\,\mathrm {mA} \end {align*}
Eine Erhöhung von \(I_\mathrm {C}\) führt zu einem Spannungsanstieg über \(R_4\), dadurch sinkt die Basisspannung von \(T_\mathrm {1}\), was \(I_\mathrm {C}\) wieder reduziert. Die negative Rückkopplung stabilisiert den Arbeitspunkt.
\begin {align*} S & = \frac {I_\mathrm {C,T1}}{U_\mathrm {T}} = \frac {0,82\,\mathrm {mA}}{26\,\mathrm {mA}} = 31,54\, \frac {\mathrm {mA}}{\mathrm {V}} \end {align*}
\begin {align*} A_\mathrm {V} & = S \cdot (-R_\mathrm {C}) = -315 \end {align*}
\begin {align*} A_\mathrm {V} & = -\frac {R_\mathrm {C}}{R_\mathrm {E}} = \frac {10\,\mathrm {k\Omega }}{2\,\mathrm {k\Omega }} = -5 \end {align*}
\begin {align*} -5 \cdot -315 = 1575 \approx 1600 \end {align*}
Ersatzschaltbild
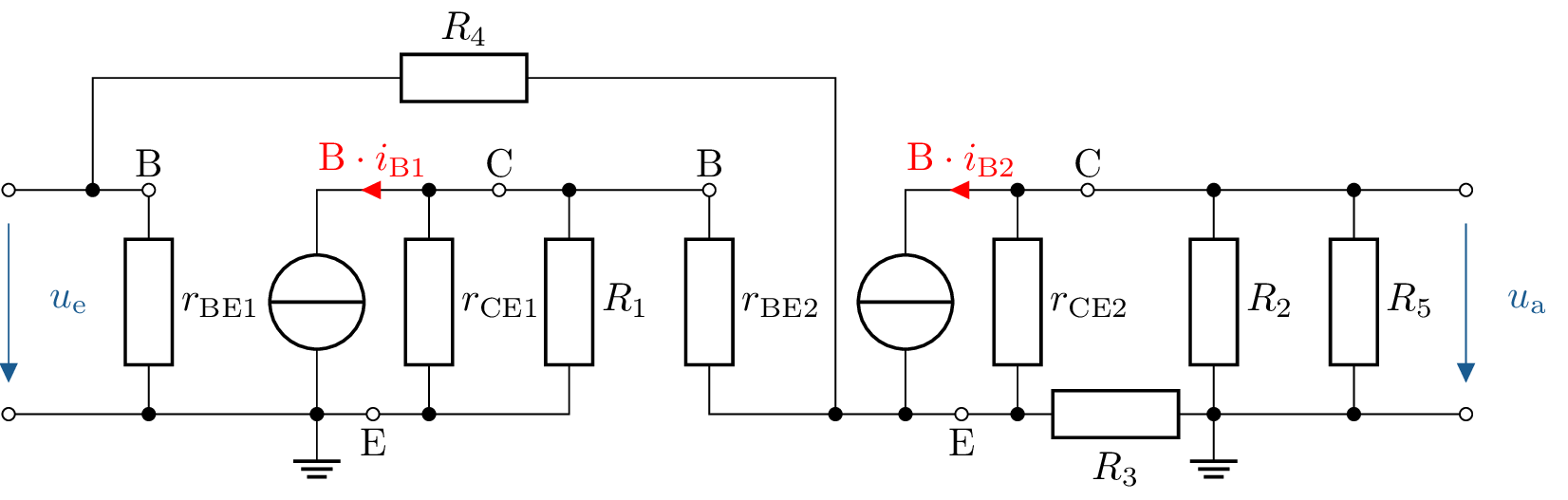
Siehe: Abschnitt ??
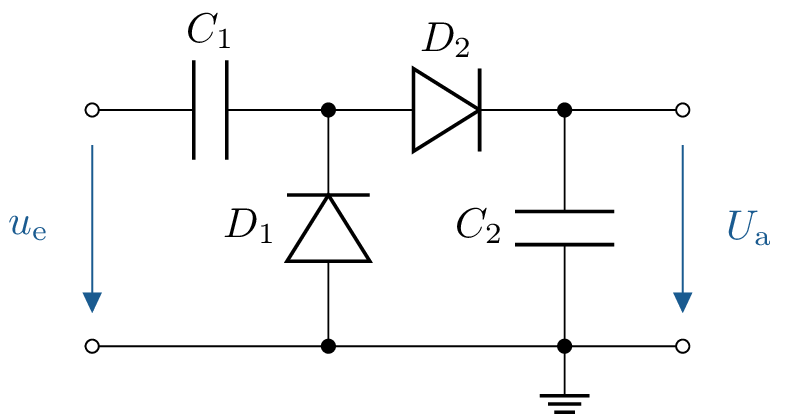
Hier eine Gleichrichterschaltung mit pn-Silizium-Dioden. Die Spannungsquelle \(V_1\) liefert sinusförmige \(50 \, \mathrm {Hz}\) Wechselspannung mit einer Amplitude von \(5\, \mathrm {V}\).
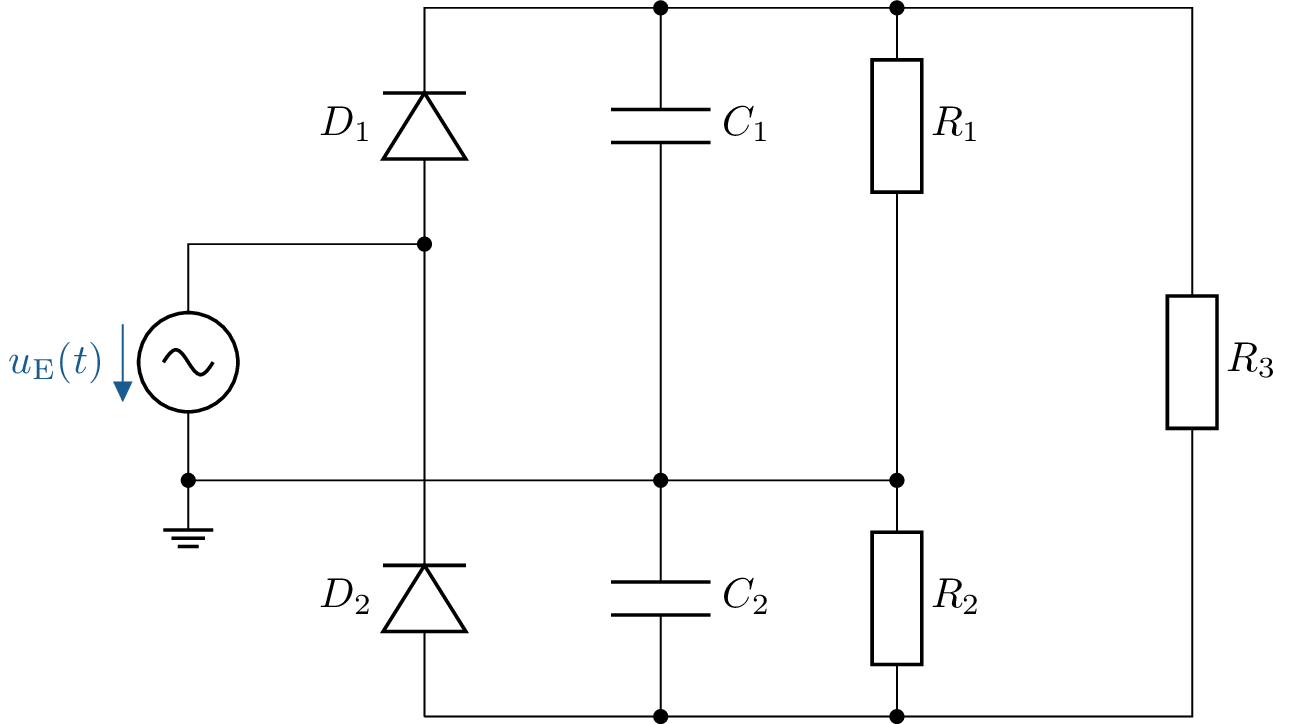
Welche Gleichspannungen treten über \(R_1\),\(R_2\) und \(R_3\) auf?
Welche Funktionen haben die Kondensatoren \(C_1\) und \(C_2\)?
Was ist der besondere Vorteil dieser Gleichrichterschaltung, z.B. für Anwendungen mit Operationsverstärkern?
Skizzieren Sie eine andere Spannungs-Verdopplungs-Schaltung, bei der die maximale positive Gleichsspannung (Ausgangsspannung) gegenüber Massepotential der speisenden Wechselspannung \(V_1\) zur Verfügung steht.
\(U_\mathrm {R1} = 4,3 \, \mathrm {V} \Rightarrow \) da \(0,7 \,\mathrm {V}\) über \(D_1\) abfallen
\(U_\mathrm {R2} = -4,3 \, \mathrm {V} \Rightarrow \) da gleiches für die negative Halbwelle
\(U_\mathrm {R3} = 8,6 \,\mathrm {V} \Rightarrow \) da \(R_3\) beide Spannungswerte aufnimmt
Die Kondensatoren \(C_1\) und \(C_2\) haben einerseits die Funktionen die Signale zu glätten, sowohl von der negativen als auch der positiven Halbwelle.
Der Vorteil dieser Gleichrichtung ist, das sowohl positive als auch negative Spannungen abgegriffen werden können.
Schaltung
Siehe: Abschnitt ??
Analysieren Sie den folgenden Gleichrichter. Zusätzlich sind die folgenden Parameter gegeben:
\(\hat {u}_\mathrm {E} = 5\,\mathrm {V}\), \(R_\mathrm {L} = 1\,\mathrm {k\Omega }\) und eine Durchlassspannung von \(U_\mathrm {f} = 0,7\,\mathrm {V}\).
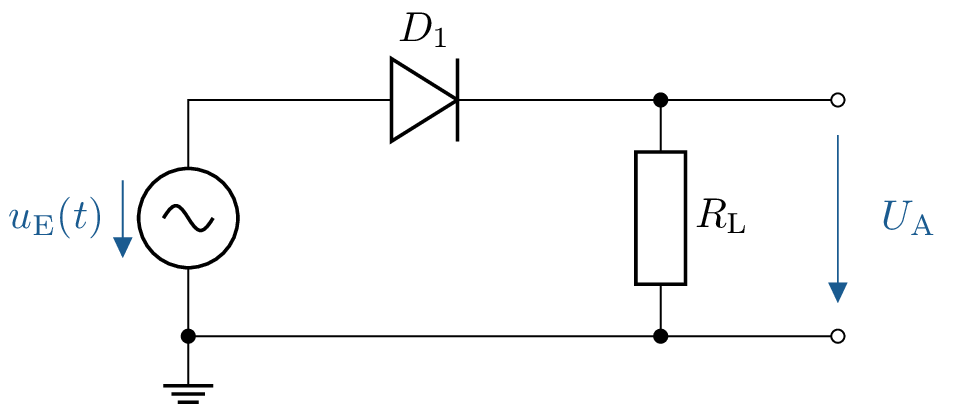
Berechnen Sie die Ausgangsspannung \(U_\mathrm {A}\).
Bestimmen Sie den durch den Lastwiderstand \(R_\mathrm {L}\) fließenden Strom \(I_\mathrm {L}\).
Berechnung der Ausgangsspannung \(U_\mathrm {A}\)
Die gegebene Schaltung besteht aus einer Diode in Vorwärtsrichtung und einem
Lastwiderstand. Die Ausgangsspannung \(U_\mathrm {A}\) entspricht der Eingangsspannung abzüglich der
Durchlassspannung: \[ U_\mathrm {A} = U_\mathrm {E} - U_\mathrm {f} \] Einsetzen der Werte: \[ U_\mathrm {A} = 5\,\mathrm {V} - 0{,}7\,\mathrm {V} = 4{,}3\,\mathrm {V} \]
Bestimmung des Laststroms \(I_\mathrm {L}\)
Der durch den Lastwiderstand \(R_\mathrm {L}\) fließende Strom berechnet sich nach dem Ohmschen Gesetz: \[ I_\mathrm {L} = \frac {U_\mathrm {A}}{R_\mathrm {L}} \]
Einsetzen der Werte: \[ I_\mathrm {L} = \frac {4{,}3\,\mathrm {V}}{1\,\mathrm {k\Omega }} = 4{,}3\,\mathrm {mA} \]
Siehe: Abschnitt ??
Analysieren Sie die Funktion der dargestellten Delon-Schaltung zur Spannungsverdopplung und berechnen Sie die Ausgangsspannung für verschiedene Eingangsspannungen. Zusätzlich sind die folgenden Parameter gegeben:
\(U_\mathrm {E1,eff}=110\,\mathrm {V}\), \(U_\mathrm {E2,eff}=230\,\mathrm {V}\) und der Durchlassspannung von \(U_\mathrm {f} = 0,7\,\mathrm {V}\).
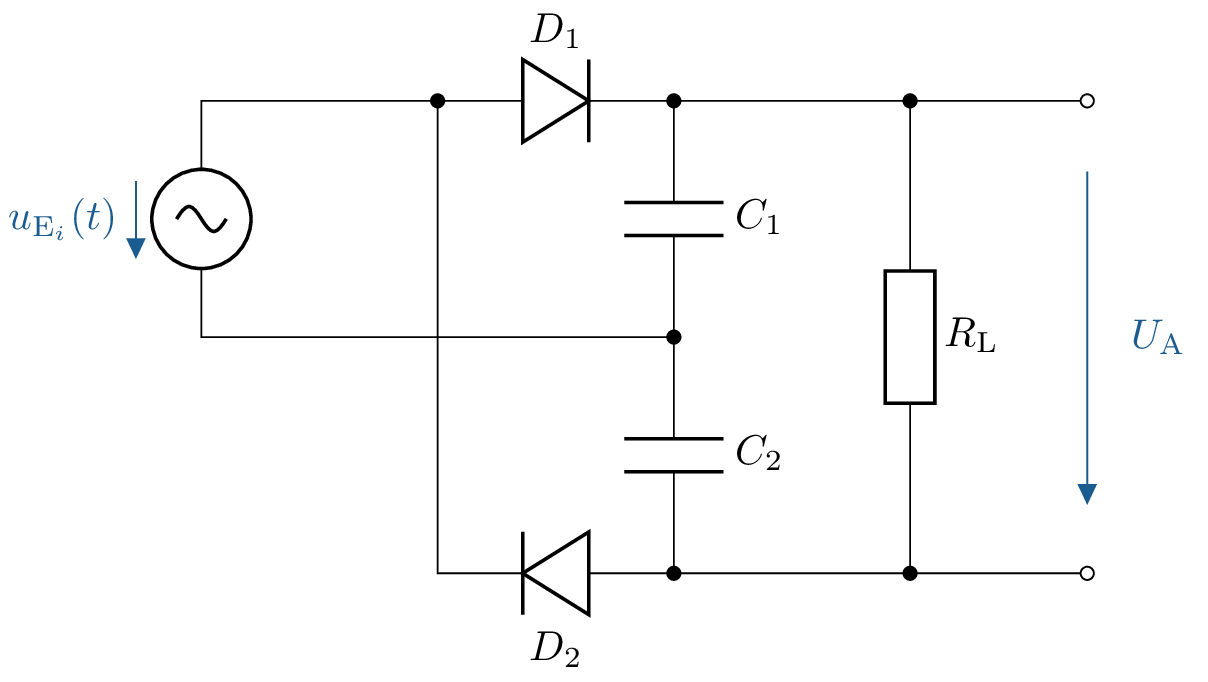
Erklären Sie das Funktionsprinzip der Delon-Schaltung und wie diese die Eingangsspannung verdoppelt.
Berechnen Sie die theoretische Leerlauf-Ausgangsspannung \(U_\mathrm {A}\) für die gegebenen Eingangsspannungen.
Diskutieren Sie, wie sich die Ausgangsspannung \(U_\mathrm {A}\) unter Lastbedingungen verhält und welche Faktoren die Spannungsstabilität beeinflussen.
Funktionsprinzip der Delon-Schaltung
Die Schaltung arbeitet als Kaskaden-Gleichrichter. Während der positiven Halbwelle der
Wechselspannung lädt sich \(C_1\) über \(D_1\) auf die Eingangsspitzen-Spannung \(\hat {U}_\mathrm {E}\) auf. Während der
negativen Halbwelle lädt sich \(C_2\) über \(D_2\) auf. Dadurch addieren sich die Spannungen von \(C_1\) und \(C_2\),
wodurch am Ausgang eine theoretische Gleichspannung von ca. \(2 \cdot \hat {U}_\mathrm {E}\) entsteht.
Berechnung der Leerlauf-Ausgangsspannung \(U_\mathrm {A}\) Die Eingangsspannung ist als Effektivwert \(U_\mathrm {E}\) gegeben. Die Spitzenwertspannung beträgt: \[ \hat {U}_\mathrm {E} = \sqrt {2} \cdot U_\mathrm {E} \] Da die Schaltung eine Spannungsverdopplung erzeugt, ergibt sich die Leerlauf-Ausgangsspannung: \[ U_\mathrm {A} = 2 \cdot (\hat {U}_\mathrm {E} - U_\mathrm {D}) = 2 \cdot (\sqrt {2} \cdot U_\mathrm {E} - 0{,}7\,\mathrm {V}) \] Für \( U_\mathrm {E} = 110\, \mathrm {V} \): \[ U_\mathrm {A} = 2 \cdot (\sqrt {2} \cdot 110\, \mathrm {V} - 0{,}7\, \mathrm {V}) \approx 308\, \mathrm {V} \] Für \( U_\mathrm {E} = 230\,V \): \[ U_\mathrm {A} = 2 \cdot (\sqrt {2} \cdot 230\,\mathrm {V} - 0{,}7\, \mathrm {V}) \approx 644\, \mathrm {V} \]
Verhalten unter Lastbedingungen Im Leerlauf bleibt die Ausgangsspannung hoch. Unter Last fällt die Spannung ab, abhängig vom Innenwiderstand der Kondensatoren, der Belastung \(R_\text {Last}\) und den Diodenverlusten. Der Spannungsabfall hängt von der Restwelligkeit ab, die durch die Lade- und Entladezeiten der Kondensatoren beeinflusst wird. Ein großer Laststrom reduziert die Spannung, da die Kondensatoren sich schneller entladen.
Faktoren, die die Spannung beeinflussen:
Innenwiderstand der Dioden
Kapazität der Kondensatoren \(C\)
Belastung durch \(R_\text {Last}\)
Netzfrequenz (\(50\, \text {Hz}\) oder \(60 \, \text {Hz}\))
Analysieren Sie das Grundverhalten eines Bipolartransistors in einer Basisschaltung. Der npn-Transistor weist einen Stromverstärkungsfaktor von \(\beta = 100\) auf, es wird ein Basisstrom von \(I_\mathrm {B} = 20\,\mathrm {\mu A}\) angenommen.
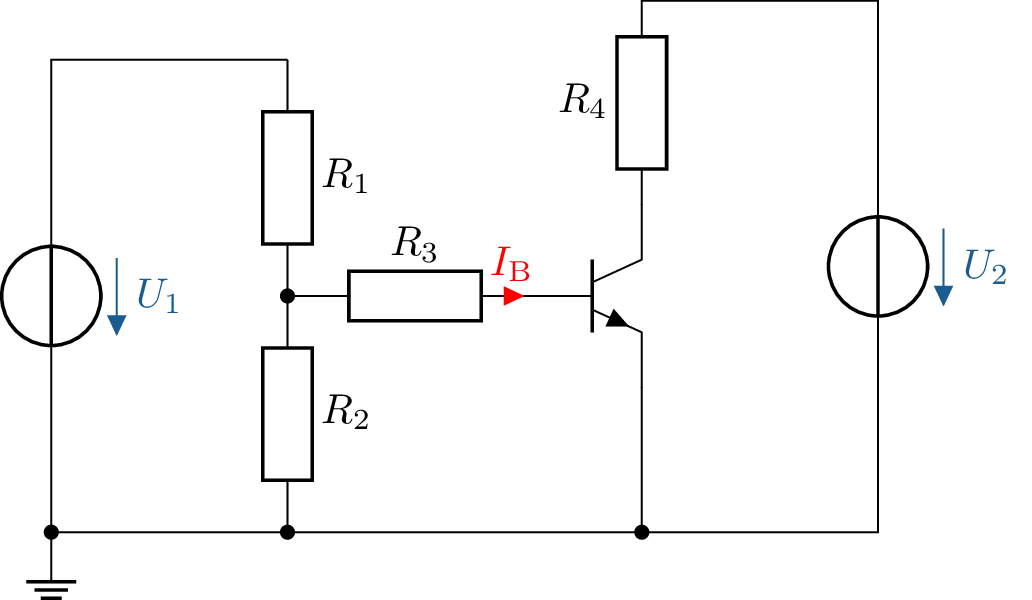
Berechnen Sie den Kollektorstrom \(I_\mathrm {C}\).
Bestimmen Sie die Kollektor-Emitter-Spannung \(U_\mathrm {CE}\), wenn der Kollektorwiderstand \(R_\mathrm {4} = 1\,\mathrm {k\Omega }\) und die Versorgungsspannung \(U_\mathrm {2} = 12\,\mathrm {V}\) beträgt.
Berechnung des Kollektorstroms \(I_\mathrm {C}\) Der Kollektorstrom eines Bipolartransistors ergibt sich aus der Beziehung: \[ I_\mathrm {C} = \beta \cdot I_\mathrm {B} \] mit den gegebenen Werten: \begin {equation*} I_\mathrm {C} = 100 \cdot 20\,\mathrm {\mu A} = 2\,\mathrm {mA} \end {equation*}
Bestimmung der Kollektor-Emitter-Spannung \(U_\mathrm {CE}\) Die Kollektor-Emitter-Spannung ergibt sich aus der Gleichung: \[ U_\mathrm {CE} = U_\mathrm {CC} - I_\mathrm {C} \cdot R_\mathrm {4} \] Einsetzen der Werte: \begin {equation*} U_\mathrm {CE} = 12\,\mathrm {V} - (2\,\mathrm {mA} \cdot 1\,\mathrm {k\Omega }) = 12\,\mathrm {V} - 2\,\mathrm {V} = 10\,\mathrm {V} \end {equation*}
Siehe: Abschnitt ??
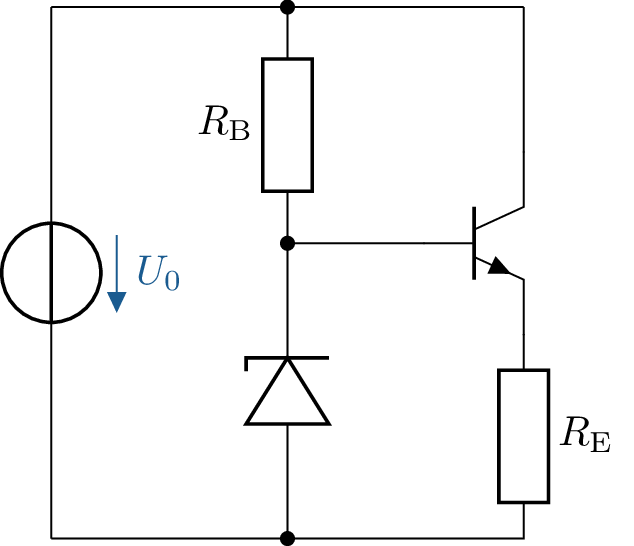
Zeichnen Sie die folgende Schaltung: Beschalten Sie einen npn-Transistor mit einem
Basisvorwiderstand von \(R_\mathrm {B} = 4,7\,\mathrm {k\Omega }\), einem Emitterwiderstand von \(R_\mathrm {E} = 1\,\mathrm {k\Omega }\) und einer Spannungsversorgung von \(U_\mathrm {0} = 15\,\mathrm {V}\).
Schalten Sie eine \(10 \,\mathrm {V}\)-Z-Diode in Sperrrichtung von der Basis auf Masse.
Verwenden Sie nur eine Spannungsversorgung, welche sowohl die Basis als auch den Kollektor
versorgt.
Berechnen Sie die Emitterspannung \(U_\mathrm {E}\), und den Emitterstrom \(I_\mathrm {E}\).
Berechnen Sie die Leistung am Emitterwiderstand \(P_\mathrm {RE}\).
Schaltung:
Berechnung der Emitterspannung \(U_\mathrm {E}\)
Die Zenerdiode fixiert die Basisspannung des Transistors auf \(U_\mathrm {Z} = 10\,\mathrm {V}\). Die Basis-Emitter-Spannung beträgt \(U_{BE} = 0,7\,\mathrm {V}\).
\begin {gather*} U_\mathrm {E} = U_\mathrm {Z} - U_\mathrm {BE} = 10\,\mathrm {V} - 0,7\,\mathrm {V} = 9,3\,\mathrm {V} \\ I_\mathrm {E} = \frac {U_\mathrm {E}}{R_\mathrm {E}} = \frac {9,3\,\mathrm {V}}{1\,\mathrm {k\Omega }} = 9,3\,\mathrm {mA} \end {gather*}
Berechnung der Leistung am Emitterwiderstand \(P_{RE}\)
\[ P_\mathrm {RE} = I_\mathrm {E}^2 \cdot R_\mathrm {E} = (9,3\,\mathrm {mA})^2 \cdot 1\,\mathrm {k\Omega } = 86,49\,\mathrm {mW} \]
Siehe: Abschnitt ??
...
 b)
b)