Einführung
Halbleiterbauelemente bilden das Rückgrat der modernen Elektronik und sind entscheidend für die Funktionsweise zahlreicher elektronischer Geräte wie Computer, Mobiltelefone und Solarzellen. Diese Bauelemente nutzen die besonderen Eigenschaften von Materialien, die weder gute Leiter noch gute Isolatoren sind, sondern dazwischen liegen – den sogenannten Halbleiter. Im Folgenden wird auf ihre Funktionsweise eingegangen, beginnend mit dem Bändermodell, welches die Energiezustände in Festkörpern beschreibt. Auf Grundlage verschiedener Eigenschaften werden weitere Halbleitermaterialien sowie deren Anwendungen erläutert. Ein grundlegendes Konzept, das eine Schlüsselrolle spielt, ist der pn-Übergang, der die Basis für eine Vielzahl von Bauelementen bildet. In diesem Kontext werden im zweiten Teil verschiedene Halbleiterbauelemente wie Dioden und Transistoren thematisiert sowie ihre Funktionen erläutert.
Lernziele: Halbleiter
Die Studierenden können
- Zusammenhänge zwischen Festkörpern und dem Bändermodell erklären.
- Vorgänge innerhalb von Halbleitern beschreiben.
- verschiedene Halbleitermaterialen und deren Eigenschaften bennen.
1 Bändermodell
Das Bändermodell ist ein grundlegendes Konzept in der Festkörperphysik, das die physikalischen Eigenschaften von Festkörpern beschreibt. Es bietet eine theoretische Grundlage für das Verständnis der elektrischen, optischen und magnetischen Eigenschaften von Materialien. Das Modell organisiert die Energiezustände von Elektronen in sogenannten Energiebändern. Diese Bänder beeinflussen maßgeblich das elektronische Verhalten des Materials. Das Bändermodell ermöglicht es, komplexe Phänomene wie Leitung, Isolation, Halbleiterverhalten und die Bildung von Oberflächen- und Grenzflächenzuständen zu verstehen und zu erklären. Im Folgenden Abschnitt werden die Grundprinzipien erläutert und ein Blick auf den Ladungsträgertransport geworfen.
Um das Bändermodell zu verstehen, soll zunächst der Bezug zum aus der Schulphysik bekannten Bohrschen Atommodell hergestellt werden. Im Bohrschen Atommodell werden die Energieniveaus von Elektronen in einem Atom als diskrete Werte angenommen. Nach diesem Modell befinden sich Elektronen auf definierten Bahnen um den Atomkern, die als Schalen bezeichnet werden. Jede Schale hat ein charakteristisches Energieniveau. Diese Energieniveaus sind quantisiert und hängen vom Abstand zum Atomkern ab. Dabei weisen Elektronen in den inneren Schalen niedrigere Energieniveaus auf als Elektronen in den äußeren Schalen. Der Zusammenhang zwischen dem Bohrschen Atommodell und dem Bändermodell ist in Abbildung 2 dargestellt.
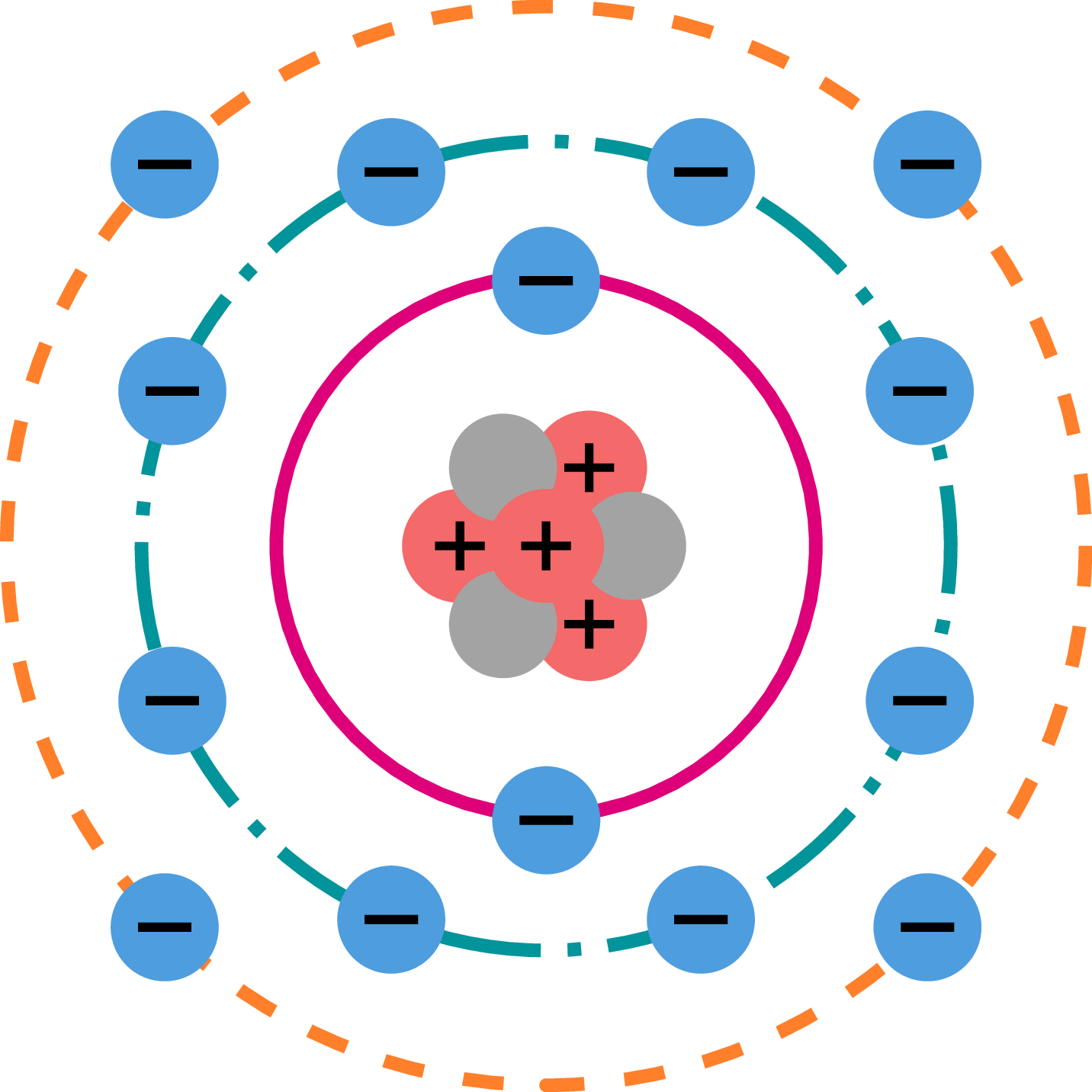

Bei einem einzelnen Atom sind die möglichen Energiezustände eindeutig definiert. Werden mindestens zwei Atome zusammengeführt, sodass sie elektrisch miteinander wechselwirken, überlappen sich deren Energiezustände. Aufgrund des Pauli-Prinzips, welches auch Ausschlussprinzip genannt wird, können zwei Elektronen allerdings nicht genau denselben Zustand annehmen, weshalb sich die Zustände minimal zueinander verschieben. Mit steigender Anzahl an Atomen steigt auch die Anzahl der verschiedenen Energiezustände in einem Festkörper. Da diese Niveaus sehr nahe beieinander liegen, werden sie zu den Energiebändern zusammengefasst. Dieser Zusammenhang ist in Abbildung 3 dargestellt.
Elektronen können nur feste Werte innerhalb der Energiebänder annehmen. In den Lücken zwischen den Bändern können sich keine Ladungsträger frei bewegen. Diese Lücken werden als „verbotener Bereich“ oder Bandlücke bezeichnet. Die Größe dieser Lücken bestimmt die elektrischen Eigenschaften des Materials. Die Energiedifferenz zwischen den Bändern entspricht der Energie, die bei Absorption oder Emission von Photonen aufgenommen oder abgegeben wird.
1.1 Einteilung von Materialien
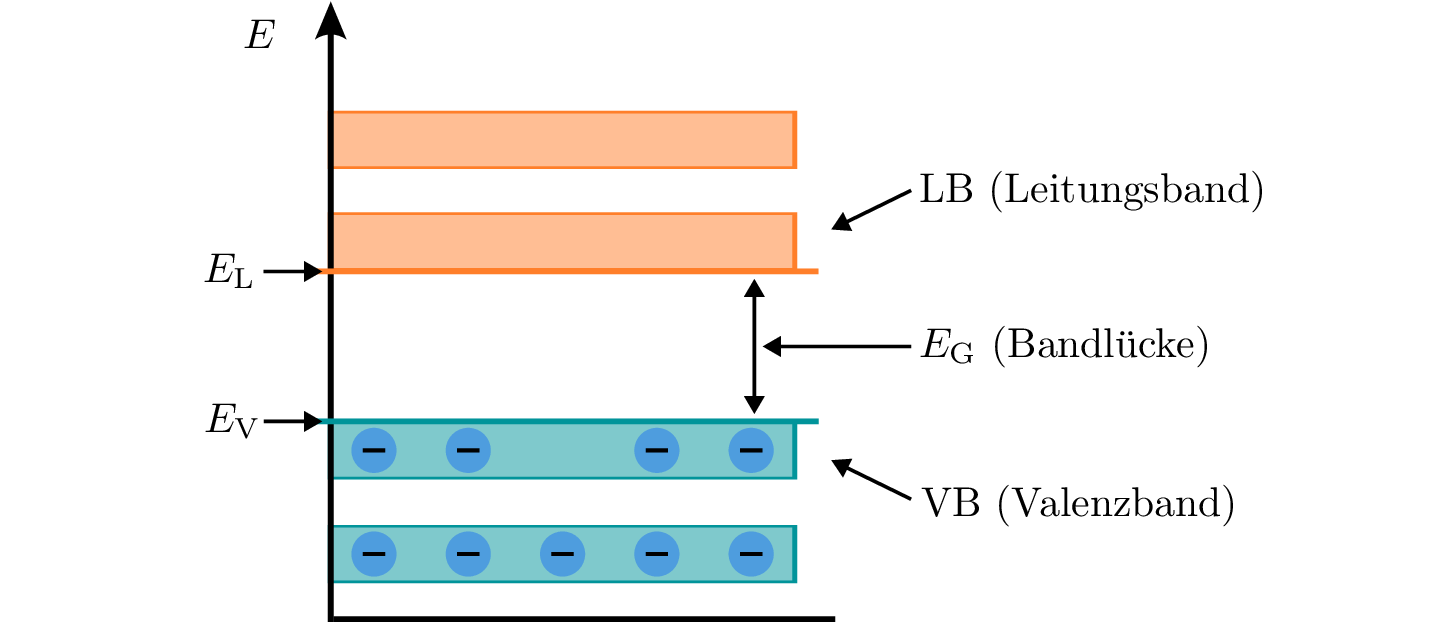
Zwei Bänder sind besonders relevant für den Ladungstransport und somit für die elektrischen Eigenschaften: das Valenzband (VB) und das Leitungsband (LB). Das Valenzband ist das Band, das die höchsten Energieniveaus enthält, die von Elektronen besetzt sind, wenn das Material bei einer Temperatur von \({0}\,\mathrm {K}\) vorliegt. Diese Elektronen sind eng an die Atomkerne gebunden und tragen nicht zum elektrischen Strom bei. Das Leitungsband liegt oberhalb des Valenzbands und enthält leere Zustände, in denen Elektronen leicht angeregt werden können, beispielsweise durch eine Erhöhung der Temperatur. Elektronen im Leitungsband können sich relativ frei durch das Material bewegen und ermöglichen somit den elektrischen Stromfluss. Die drei grundlegenden Klassen Leiter, Halbleiter und Isolatoren lassen sich durch den Abstand (Bandlücke) dieser beiden relevanten Bänder definieren. In der folgenden Abbildung ist das Bändermodell eines Materials bei \({0}\,\mathrm {K}\) dargestellt, mit den relevanten Größen und Bezeichnungen.
Die Besetzung der Bänder mit Elektronen hängt neben der Temperatur von weiteren Faktoren ab. Vor allem durch gezielte Verunreinigung mit Fremdatomen, sogenannter Dotierung, kann die Leitfähigkeit beeinflusst werden. Die Fremdatome bringen freie Ladungsträger ein und führen zu zusätzlichen Energieniveaus innerhalb der Bandlücke, von denen aus zum Beispiel leichter Ladungsträger das Band wechseln können (siehe Abschnitt 3). Neben den bisher gezeigten Energieniveaus ist das Ferminiveau eine weitere wichtige Größe. Dieses gibt den Energiewert an, bei dem Elektronen eine Aufenthaltswahrscheinlichkeit von \(1/{1}{2}\) aufweisen. Bei einem undotierten Halbleiter liegt das Niveau mittig zwischen Valenz- und Leitungsband, bei dotierten Halbleitern verschiebt sich das Niveau in Richtung des jeweiligen Dotierbands.
Leiter sind Materialien, deren Valenz- und Leitungsbänder aneinandergrenzen oder überlappen, was bedeutet, dass Elektronen leicht zwischen den Bändern wechseln können. Diese Nähe ermöglicht eine hohe Leitfähigkeit, da Elektronen sich frei durch das Material bewegen können. Metalle wie Kupfer und Aluminium sind typische Beispiele für Leiter.
Halbleiter haben eine kleine Bandlücke, die zwischen der des Leiters und der des Isolators liegt. Diese Bandlücke ist so groß, dass in dem Material bei niedrigen Temperaturen kein elektrischer Strom fließt, da Elektronen nicht genügend Energie haben, um ins Leitungsband angeregt zu werden. Mit steigender Temperatur oder durch das Einbringen von Fremdatomen kann die Leitfähigkeit jedoch deutlich erhöht werden. Halbleiter wie Silizium und Germanium sind häufig eingesetzte Materialien in der Elektronikindustrie.
Isolatoren haben eine große Bandlücke, die dazu führt, dass das Valenzband vollständig besetzt ist und das Leitungsband leer ist. Dadurch können Elektronen nur schwer ins Leitungsband angeregt werden, selbst bei hohem Energieeintrag. Isolatoren wie Glas und Keramik zeigen daher eine sehr geringe Leitfähigkeit.
Im Folgenden sind beispielhaft die Bändermodelle mit den Valenz- und Leitungsbändern der drei genannten Klassen dargestellt.
Merke:
- Ladungsträger können nur definierte Energieniveaus im Festkörper besetzen.
- Bei \(T=\mathrm {0\,K}\) ist das Valenzband das höchste besetzte Energieniveau, das darüberliegende Leitungsband beinhaltet keine freien Ladungsträger.
- Materialien können über die Bandlücke, in Leiter, Halbleiter und Isolatoren kategorisiert werden.
2 Halbleitermaterialien
Die Gitterstrukturen von Halbleitermaterialien spielen eine entscheidende Rolle in Bezug auf deren elektronischen und mechanischen Eigenschaften. Im Folgenden werden die Gitterstrukturen von Silizium und Galliumarsenid (GaAs) betrachtet. Silizium ist aufgrund seiner hohen Verfügbarkeit und dem damit verbundenen geringen Preis das am weitesten verbreitete Halbleitermaterial. Darüber hinaus lässt es sich sehr gut verarbeiten und seine elektrischen Eigenschaften lassen sich gut beeinflussen. Galliumarsenid hingegen dient als Beispiel für einen Verbindungshalbleiter aus Elementen der III. und V. Hauptgruppe des Periodensystems, entsprechend wird ein solcher Halbleiter auch als III/V-Verbindungshalbleiter bezeichnet. Die einzelnen Elemente weisen kein Halbleiterverhalten auf, erst bei besonderer Anordnung und besonderem Atomverhältnis bildet sich das Halbleiterverhalten aus.
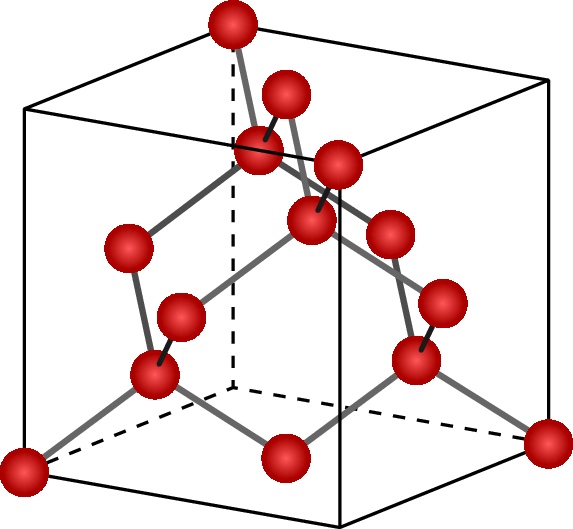
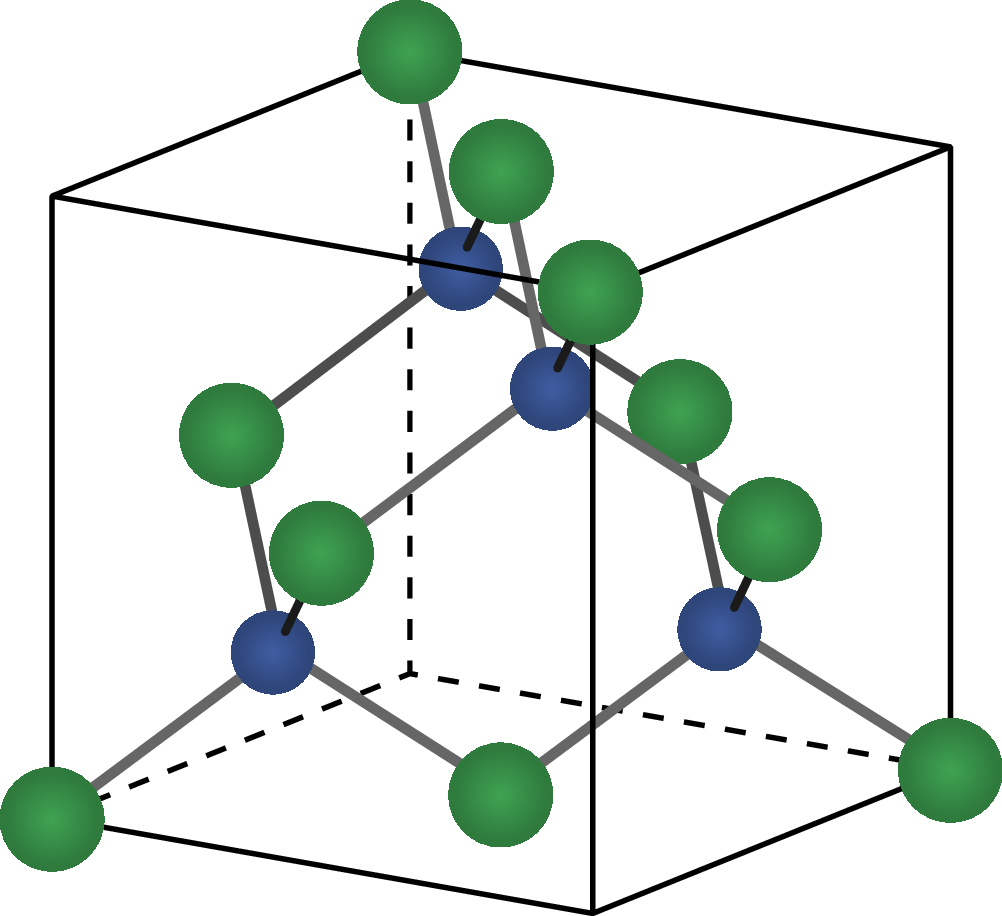
Silizium hat eine Diamantgitterstruktur, bei der jedes Siliziumatom von vier benachbarten Atomen in einer tetraedrischen Anordnung umgeben ist. Diese Struktur führt zu einer stabilen und robusten Kristallstruktur, die eine hohe mechanische Stabilität aufweist. Darüber hinaus ermöglicht die Anordnung eine hohe Beweglichkeit der freien Elektronen in alle Raumrichtungen.
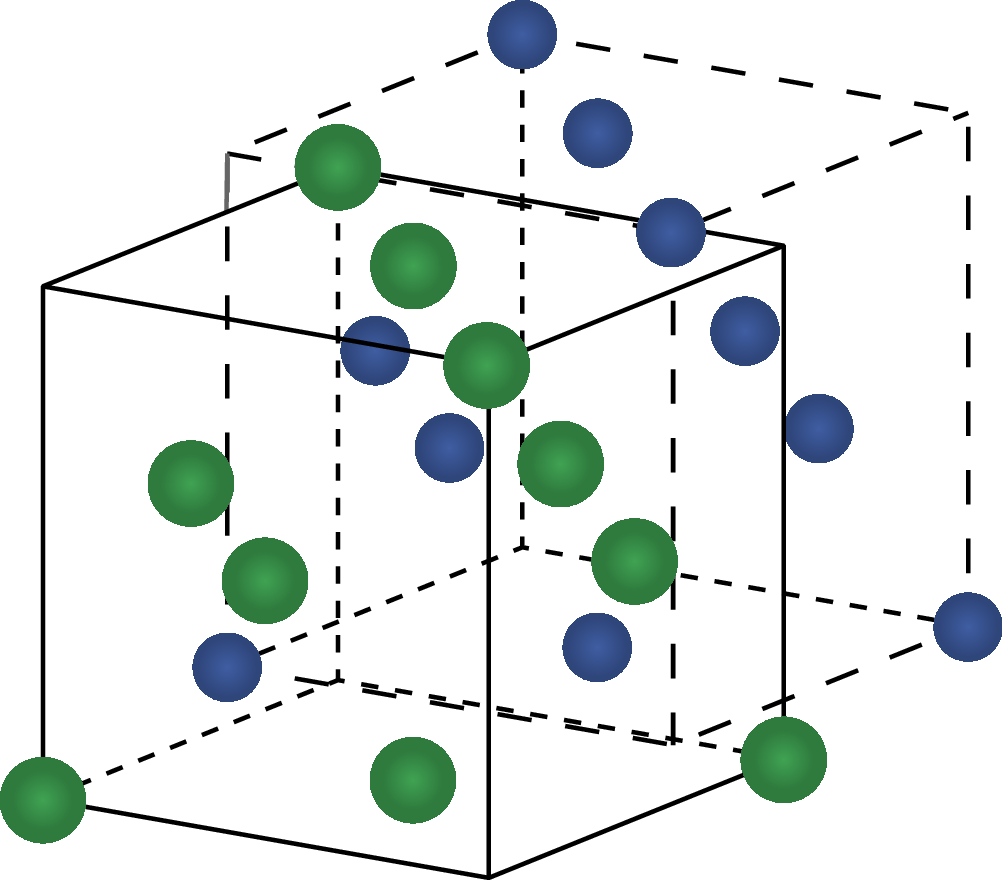
Im Gegensatz dazu sind bei Galliumarsenid die Gallium- und Arsenatome so angeordnet, dass sie zwei ineinander verschobene kubisch flächenzentrierte Gitter darstellen, die sogenannte Zinkblende-Gitterstruktur. Die resultierende Anordnung ist identisch mit der Diamantgitterstruktur, jedoch mit dem regelmäßigen Wechsel zwischen zwei Ionenarten. Diese Struktur ermöglicht eine geringe Bandlücke, was zu einer geringen Anregungsenergie führt, die notwendig ist, um Elektronen zwischen Valenz- und Leitungsband zu verschieben.
Merke:
- Silizium ist das am weitesten verbreitete Halbleitermaterial.
- Verbindungshalbleiter bestehen aus zwei Materialen, die in bestimmter Kombination Halbleiterverhalten aufweisen.
- Silizium ist aus der IV. Hauptguppe des Periodensystem, Verbindungshalbleiter typischerweise aus der III. und V. Hauptgruppe.
Die folgende Tabelle bietet einen Überblick über einige der wichtigsten Halbleitermaterialien und Verbindungshalbleiter sowie ihre wesentlichen Eigenschaften und Anwendungen. Diese Materialien spielen eine entscheidende Rolle in der modernen Elektrotechnik und werden in einer Vielzahl von Anwendungen eingesetzt, von Mikrochips und Solarzellen bis hin zu Hochfrequenzschaltungen und LED-Beleuchtung. Die Tabelle enthält Informationen über die Bandlücke, Ladungsträgerdichte (Eigenleitungsdichte), Elektronen- und Löcherbeweglichkeit sowie charakteristische Eigenschaften und Anwendungen jedes Materials. Die Beweglichkeit beschreibt die Geschwindigkeit, mit der sich Ladungsträger unter Einfluss eines elektrischen Feldes durch das Material bewegen. Bei Löchern handelt es sich um quasi-partielle Zustände, die als positive Ladungsträger betrachtet werden. Es handelt sich hierbei nicht um tatsächliche positive Ladungsträger, sondern um lokale Bereiche, die aufgrund eines fehlenden Elektrons als positiv geladen betrachtet werden können.
| Material | \(\boldsymbol {E_\mathrm {G}}\) | \(\boldsymbol {n}\) | \(\boldsymbol {\mu _\mathrm {e}}\) | \(\boldsymbol {\mu _\mathrm {p}}\) | Eigenschaften | Anwendungen |
| Silizium (Si) | \(1,1\) | \(1\cdot 10^{10}\) | \(1500\) | \(450\) | Häufigste Halbleitermaterial | Mikrochips, |
| Germanium (Ge) | \(0,7\) | \(2\cdot 10^{13}\) | \(3900\) | \(1900\) | Früher häufig in elektronischen Geräten verwendet | Transistoren, Infarot-Detektoren |
| Gallium- arsenid (GaAs) | \(1,43\) | \(2\cdot 10^6\) | \(8500\) | \(400\) | Direkter Bandübergang, Einsatz bei hohen Frequenzen | Hochfrequenzschaltungen,
LEDs, |
| Indium- phosphid (InP) | \(1,35\) | \(1\cdot 10^{16}\) | \(5000\) | \(200\) | Direkter Bandübergang, Hohe Lichtabsorption bei Wellenlängen im Bereich von \(\mathrm {1,3-1,55\,\mu m}\) | Optoelektronik, Solarzellen |
| Gallium- nitrid (GaN) | \(3,4\) | \(1\cdot 10^{-10}\) | \(380\) | \(-\) | Hohe thermische und chemische Stabilität, Hohe elektronische Durchbruchsfeldstärke | Leistungselektronik, LED-Beleuchtung, Displays |
| Silizium- karbid (SiC) | \(3,0\) | \(1\cdot 10^{-7}\) | \(500\) | \(-\) | Extrem hohe thermische Stabilität, Hohe elektronische Durchbruchsfeldstärke | Leistungs- elektronik, Hochtemperaturanwendung |
3 Ladungsträgertransport
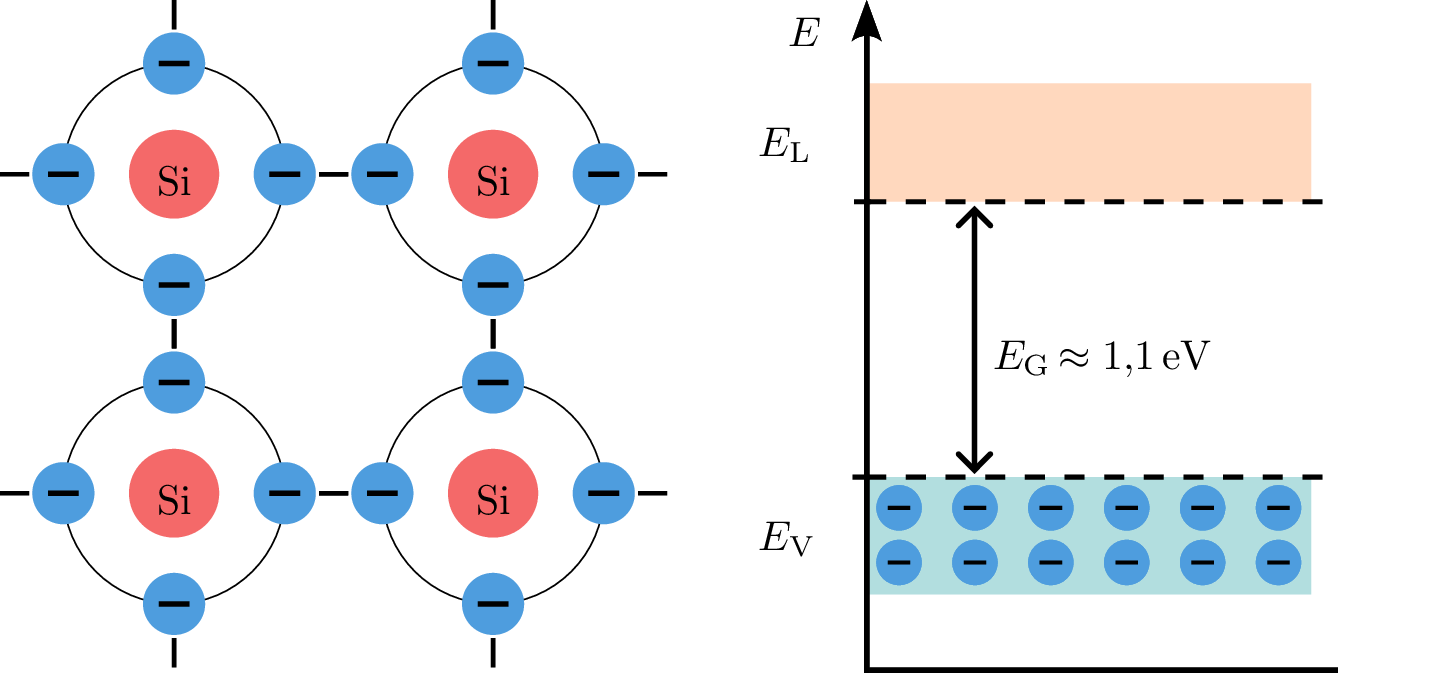
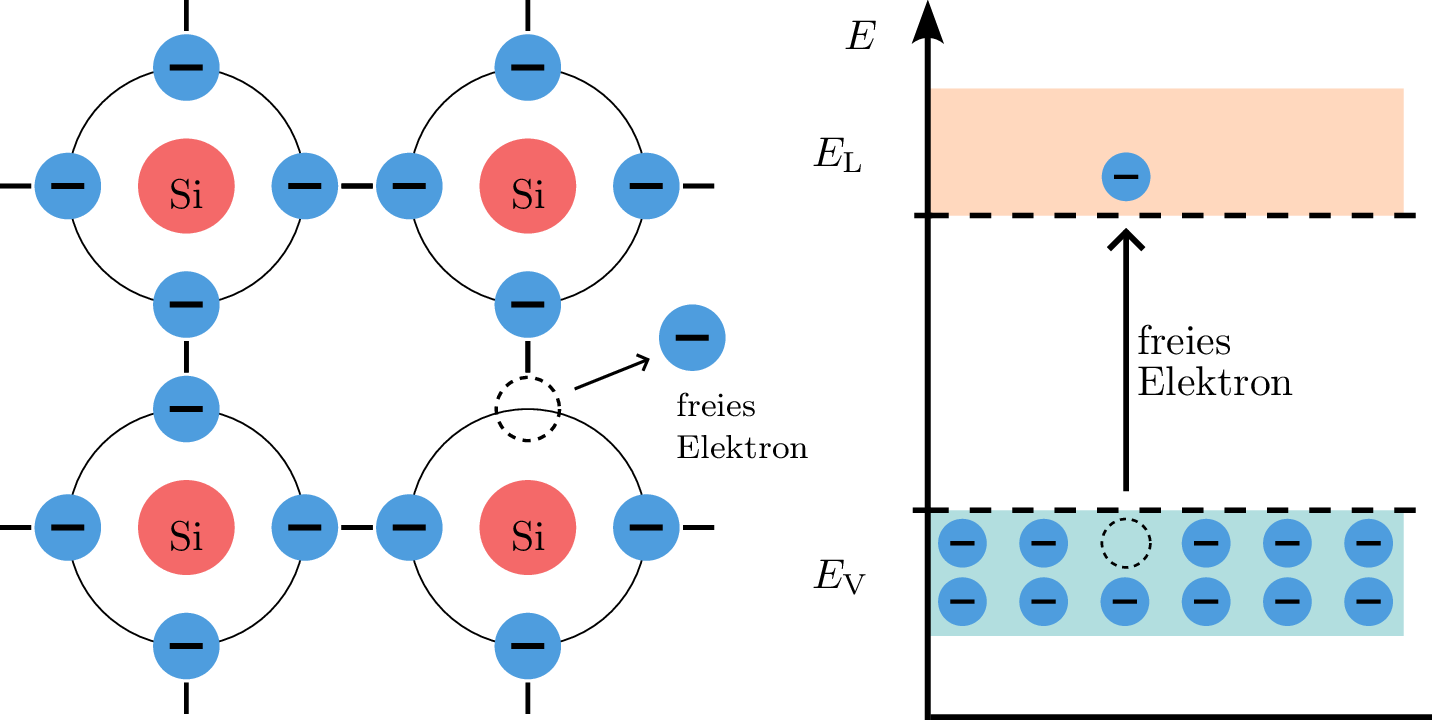
Bei einer Temperatur von \(\mathrm {0\,K}\) (absoluter Nullpunkt) weisen Halbleiter wie Silizium ein vollständig besetztes Valenzband mit dem Energieniveau \(E_\mathrm {V}\) und ein leeres Leitungsband mit dem Energieniveau \(E_\mathrm {L}\) auf. Dies bedeutet, dass alle Elektronen im Valenzband gebunden und keine freien Ladungsträger vorhanden sind. Das Bändermodell zeigt eine deutliche Bandlücke zwischen dem Valenz- und dem Leitungsband. Wenn die Temperatur über \(\mathrm {0\,K}\) erhöht wird, steigt die Beweglichkeit der Elektronen im Kristallgitter. Einige Elektronen im Valenzband können durch thermische Anregung Energie erhalten und in das Leitungsband übergehen, wodurch freie Elektronen und Löcher erzeugt werden. Diese freien Ladungsträger tragen zur Leitfähigkeit des Halbleiters bei.
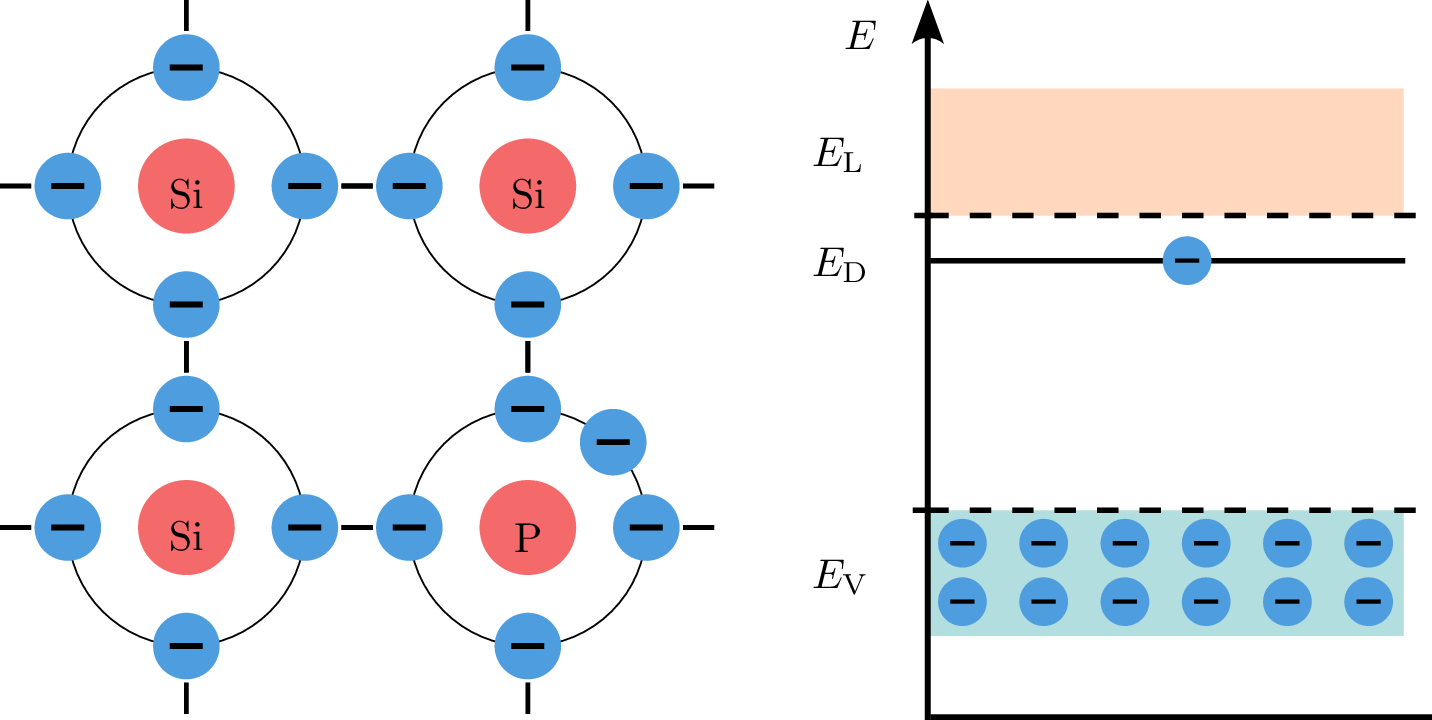
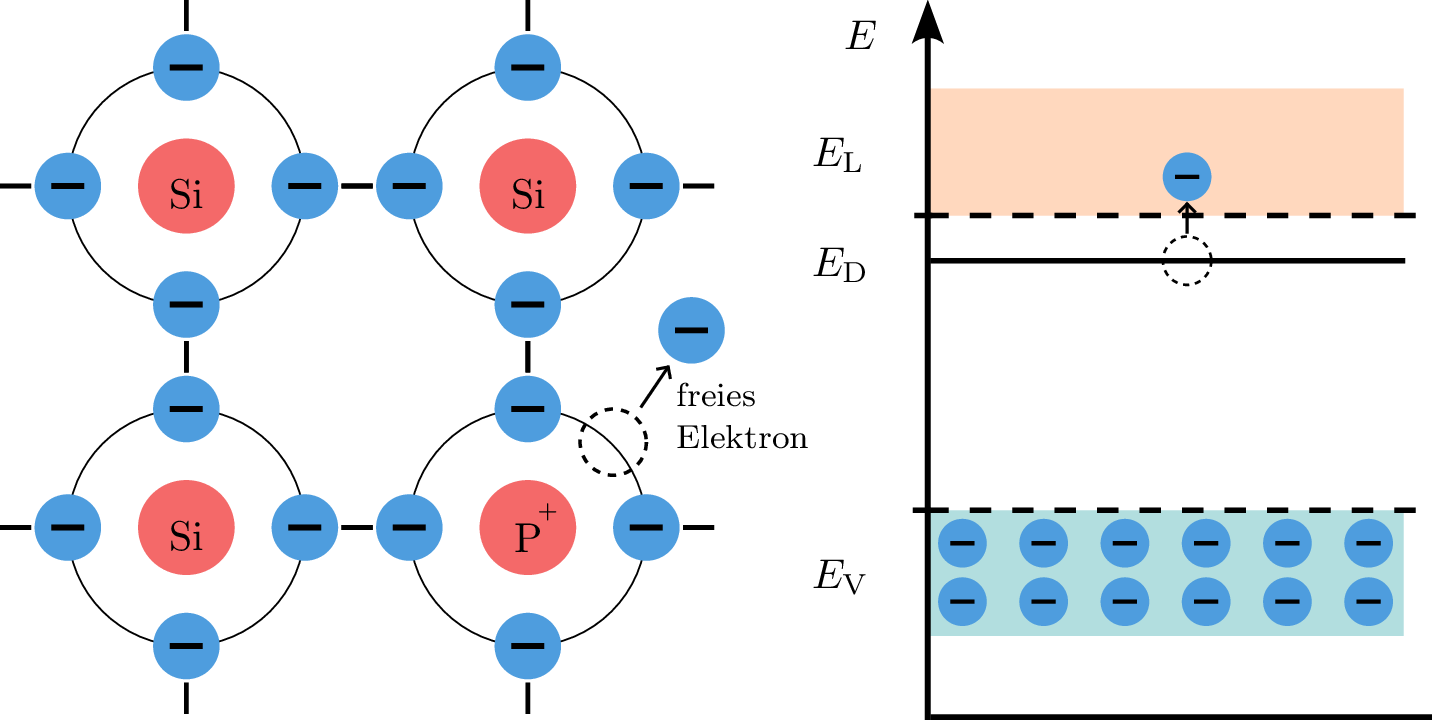
Bei der Zugabe von Phosphor zu Silizium führt dies dazu, dass das Phosphoratom fünf Valenzelektronen einbringt (n-dotiert), eins mehr als Silizium. Das in diesem Fall überschüssige Elektron wird locker an das Kristallgitter gebunden und kann leicht von äußeren Energiequellen entfernt werden, wodurch es zu einem Donator von freien Elektronen wird. Diese Elektronen befinden sich im Donatorband (\(E_\mathrm {D}\)), unmittelbar unterhalb des Leitungsbands. Bei einer Temperatur über \(\mathrm {0\,K}\) verfügen die Elektronen aufgrund der thermischen Anregung über ausreichend Energie, um die Bandlücke zu überwinden und ins Leitungsband zu gelangen. Die durch den Phosphor bereitgestellten Elektronen erleichtern diesen Prozess. Daher erhöht sich die Leitfähigkeit des Materials.
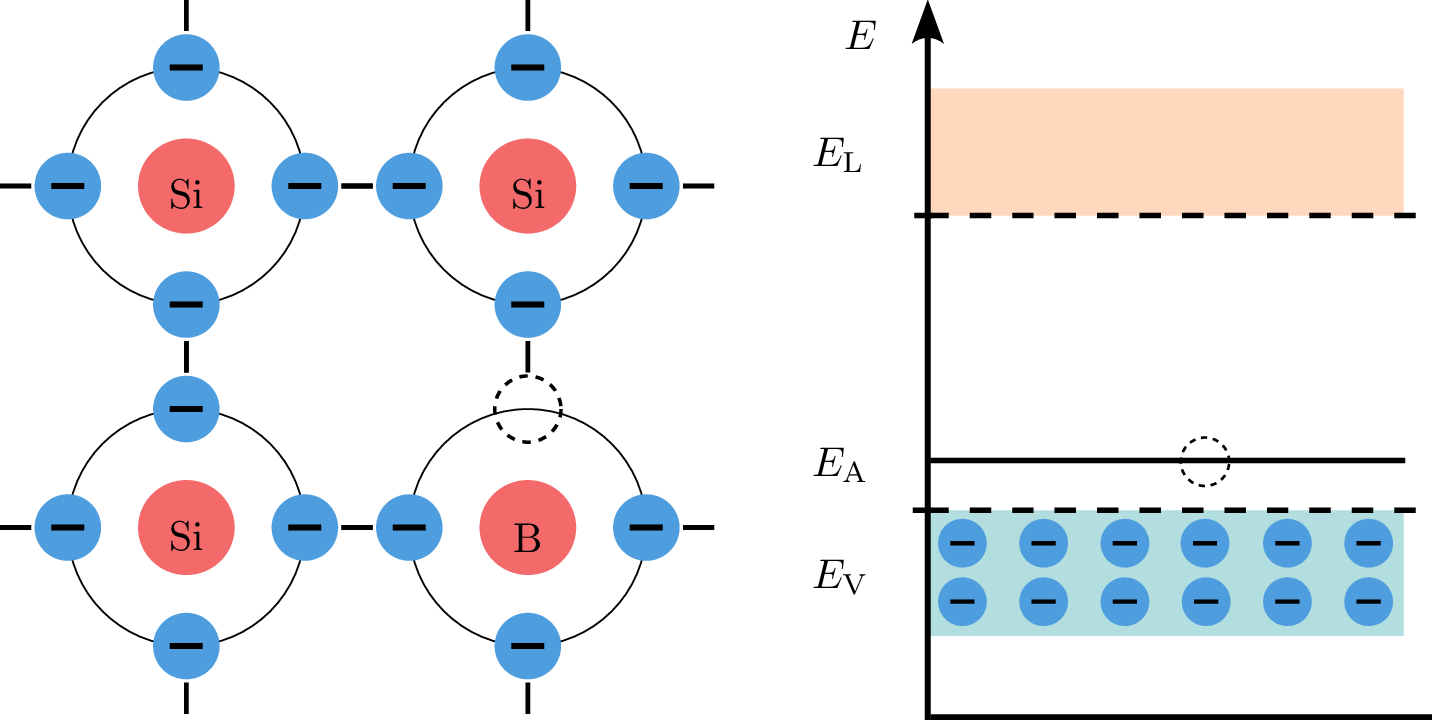
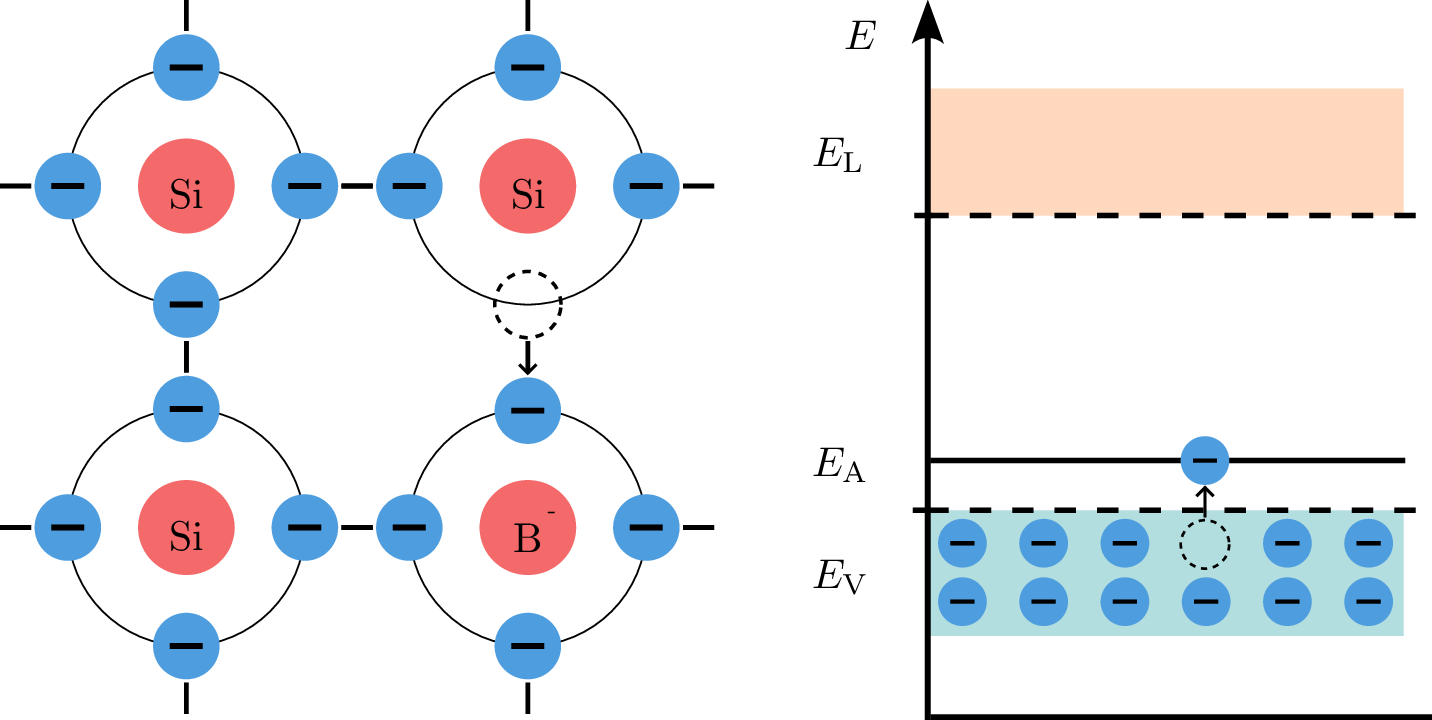
Bei der Zugabe von Bor zu Silizium (p-Dotierung) hat das Boratom nur drei Valenzelektronen, eins weniger als Silizium. Dadurch entsteht im Kristallgitter ein Loch im Valenzband, das als Akzeptor von Elektronen wirkt. Bei \({0}\,\mathrm {K}\) sind jedoch keine thermisch erzeugten Löcher vorhanden. Bei einer Temperatur über \({0}\,\mathrm {K}\) führt die thermische Energie dazu, dass Elektronen aus dem Valenzband ins Akzeptorband (\(E_\mathrm {A}\)) gelangen, wodurch Löcher im Valenzband zurückbleiben. Diese Löcher wirken wie positive Ladungsträger und erhöhen die Leitfähigkeit des Materials.
Merke:
- Durch thermische Anregung können freie Elektronen entstehen, die zum Ladungsträgertransport beitragen.
- Dotierung ist das gezielte Einbringen von Fremdatomen mit mehr oder weniger Valenzelektronen als das Ausgangsmaterial.
- Für n-Dotierung kann Phosphor und für p-Dotierung Bor genutzt werden.
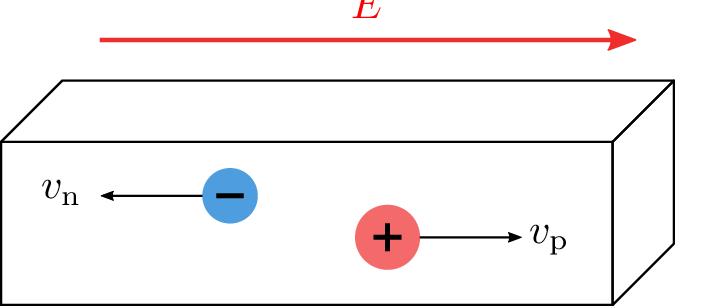
Neben den zuvor genannten Vorgängen innerhalb des Kristallgitters, die den Ladungsträgertransport durch zusätzliche Ladungsträger ermöglichen, sind zwei weitere wichtige Größen der Driftstrom und der Diffusionsstrom. Driftstrom in einem Halbleiter tritt aufgrund der Bewegung geladener Teilchen unter dem Einfluss eines äußeren elektrischen Feldes auf. Wenn ein elektrisches Feld an einem Halbleiter angelegt wird, wirkt eine Kraft auf die freien Ladungsträger (Elektronen und Löcher), die sie, je nach Vorzeichen oder Ladung, in Feldrichtung beschleunigt oder deren Bewegung verlangsamt. Für Elektronen im Leitungsband bedeutet dies, dass sie unter dem Einfluss des elektrischen Feldes in Richtung der positiven Elektrode (Anode) driften. Für Löcher im Valenzband bedeutet dies eine Drift in Richtung der negativen Elektrode (Kathode). Für eine bessere Vergleichbarkeit wird in der folgenden Abbildung das Loch als positiver Ladungsträger dargestellt. Die Driftgeschwindigkeit der Ladungsträger hängt von der Stärke des angelegten elektrischen Feldes und von der Beweglichkeit der Ladungsträger im Halbleitermaterial ab. Es ist wichtig zu beachten, dass der Driftstrom nur einen Teil des Gesamtstroms in einem Halbleiter ausmacht.
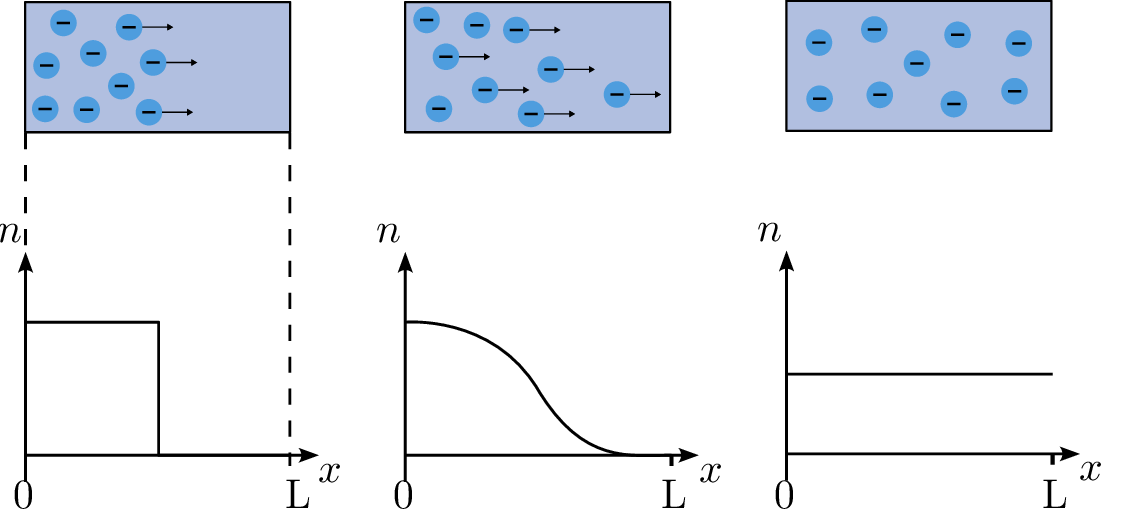
Der andere Teil des Stroms entsteht durch Diffusion, was die Bewegung von Ladungsträgern aufgrund von Konzentrationsunterschieden darstellt. In vielen Halbleiterbauelementen wie Dioden und Transistoren wirken Drift- und Diffusionsströme zusammen, um das Verhalten des Bauelements zu bestimmen. Beim Diffusionsstrom bewegen sich freie Elektronen oder Löcher von Bereichen hoher Konzentration zu Bereichen niedriger Konzentration, ähnlich wie bei der Diffusion von Teilchen in einem Konzentrationsgradienten. Elektronen im n-dotierten Halbleiter diffundieren von Regionen hoher zu Regionen niedriger Elektronenkonzentration. Umgekehrt bewegen sich bei einem p-dotierten Halbleiter Löcher von Regionen hoher Lochkonzentration zu Regionen niedriger Konzentration.
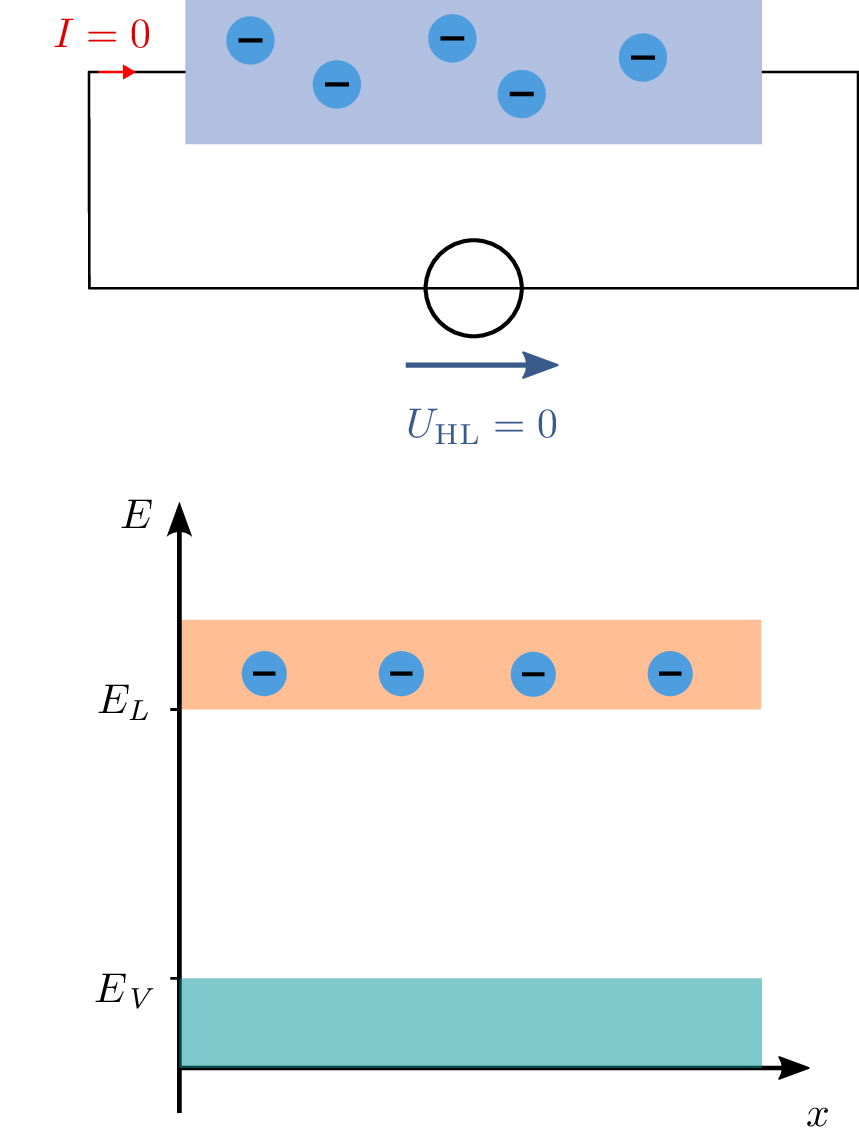
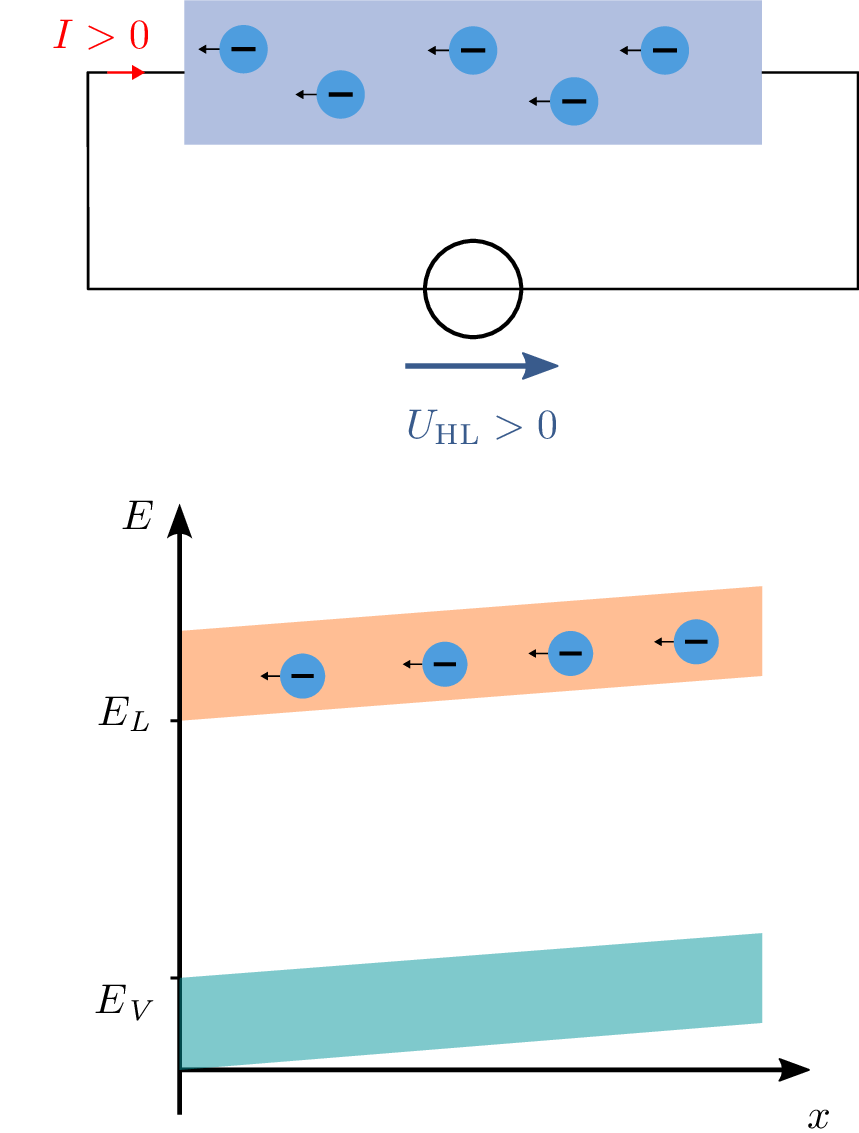
Abschließend wird in diesem Abschnitt der Ladungstransport im Bänderdiagramm bei einer angelegten Spannung betrachtet. Bislang wurde das Bänderdiagramm ausschließlich im Zustand des thermodynamischen Gleichgewichts analysiert. Es wird der allgemeine Fall betrachtet, in dem ein Strom durch den Halbleiter fließt. Als Beispiel dient ein homogener, n-dotierter Halbleiter. Anfänglich liegt keine Spannung am Halbleiter an, wodurch auch kein elektrischer Strom fließt. Das Bänderdiagramm über den Ort x zeigt daher einen Verlauf ähnlich dem in Abbildung 13 links, wobei mögliche Randeffekte an den Kontakten nicht berücksichtigt sind. Die Bänder eines Halbleiters ohne angelegte Spannung sind horizontal ausgerichtet. Sobald jedoch eine Spannung angelegt wird, verschiebt sich das Bänderdiagramm, was dazu führt, dass die Elektronen in Richtung niedrigerer Energie wandern.
Merke:
- Driftstrom ist der Ladungsträgertransport aufgrund eines elektrischen Feldes.
- Diffusionsstrom ist die Bewegung von Ladungsträgern aufgrund eines Konzentrationsunterschiedes.
- Drift- und Diffusionsstrom ergeben zusammen den Gesamtstrom.
- Eine externe Spannung führt zu einer Verschiebung des Bändermodells.
4 pn-Übergang
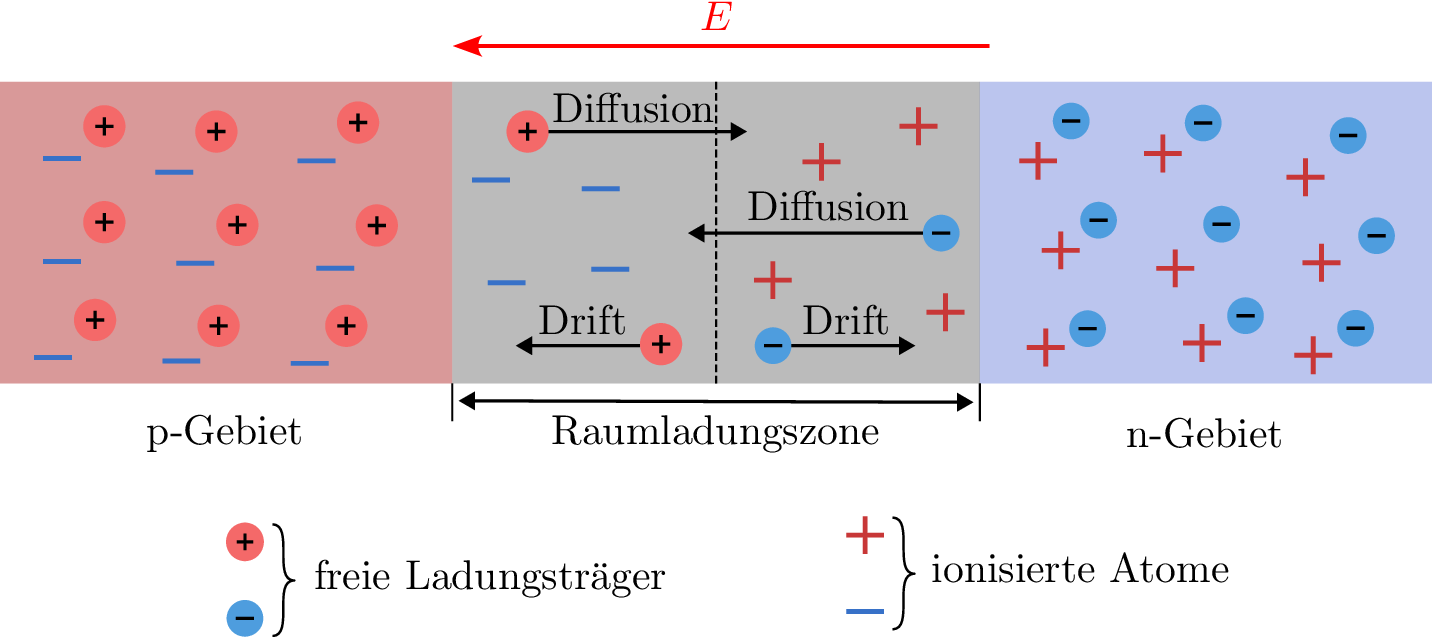
Der pn-Übergang ist das zentrale Element von Halbleiterbauelementen wie Dioden und Transistoren. Er entsteht durch die Verbindung von zwei unterschiedlich dotierten Halbleiterschichten, einer p-dotierten und einer n-dotierten Schicht. Der Übergang zwischen diesen Schichten wird als pn-Übergang bezeichnet. Im pn-Übergang kommt es zur Diffusion von freien Ladungsträgern: Elektronen aus der n-dotierten Schicht diffundieren zur p-dotierten Schicht und Löcher aus der p-dotierten Schicht diffundieren zur n-dotierten Schicht. Dieser Diffusionsprozess führt dazu, dass sich im Übergangsbereich eine sogenannte Raumladungszone (RLZ) bildet. In Abbildung 14 ist dieser Vorgang dargestellt. Die RLZ ist eine schmale Region um den pn-Übergang herum, in der positive Ionen aus der n-Schicht und negative Ionen aus der p-Schicht verbleiben, nachdem die Diffusion abgeschlossen ist. In dieser Zone gibt es keine freien Ladungsträger, da die positiven und negativen Ladungen sich gegenseitig neutralisieren. Dadurch entsteht ein elektrisches Feld (\(\vec {E}\)), das sowohl einen Driftstrom erzeugt als auch die Diffusion von weiteren Ladungsträgern unterdrückt. Die Raumladungszone wirkt wie eine Sperrschicht und verhindert den Stromfluss in Sperrrichtung.
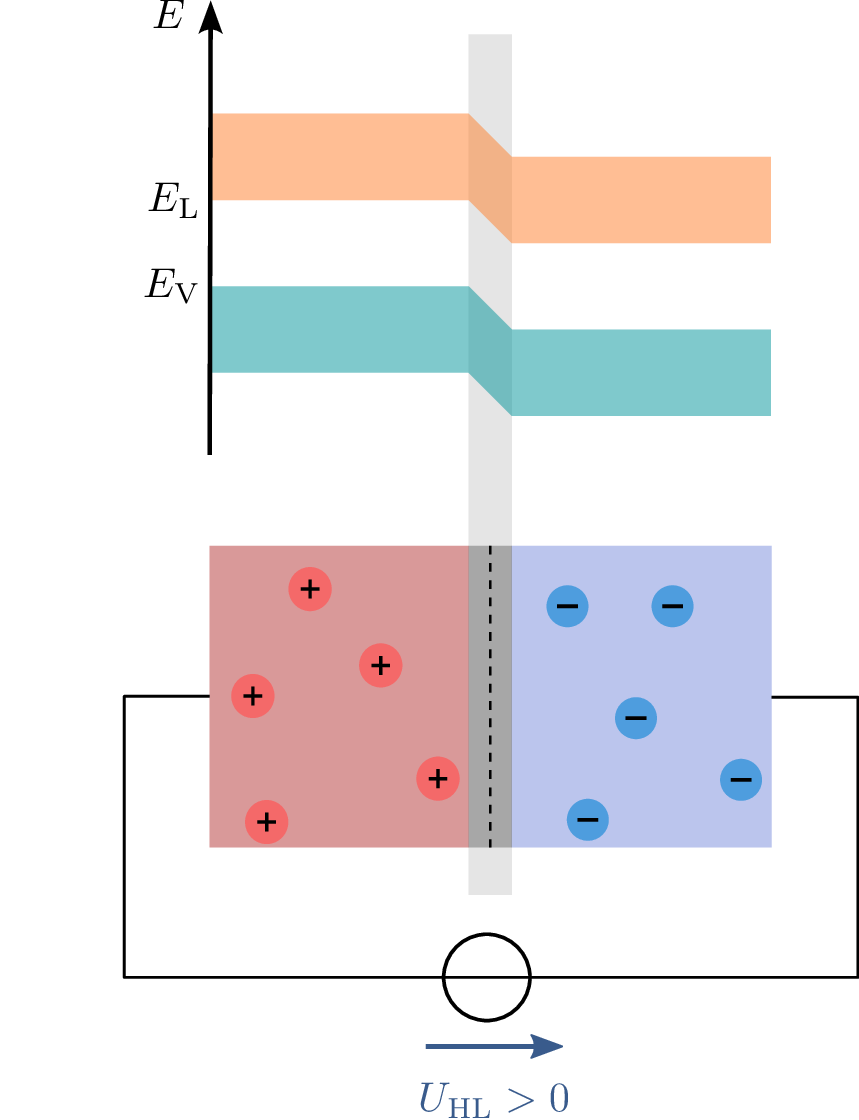
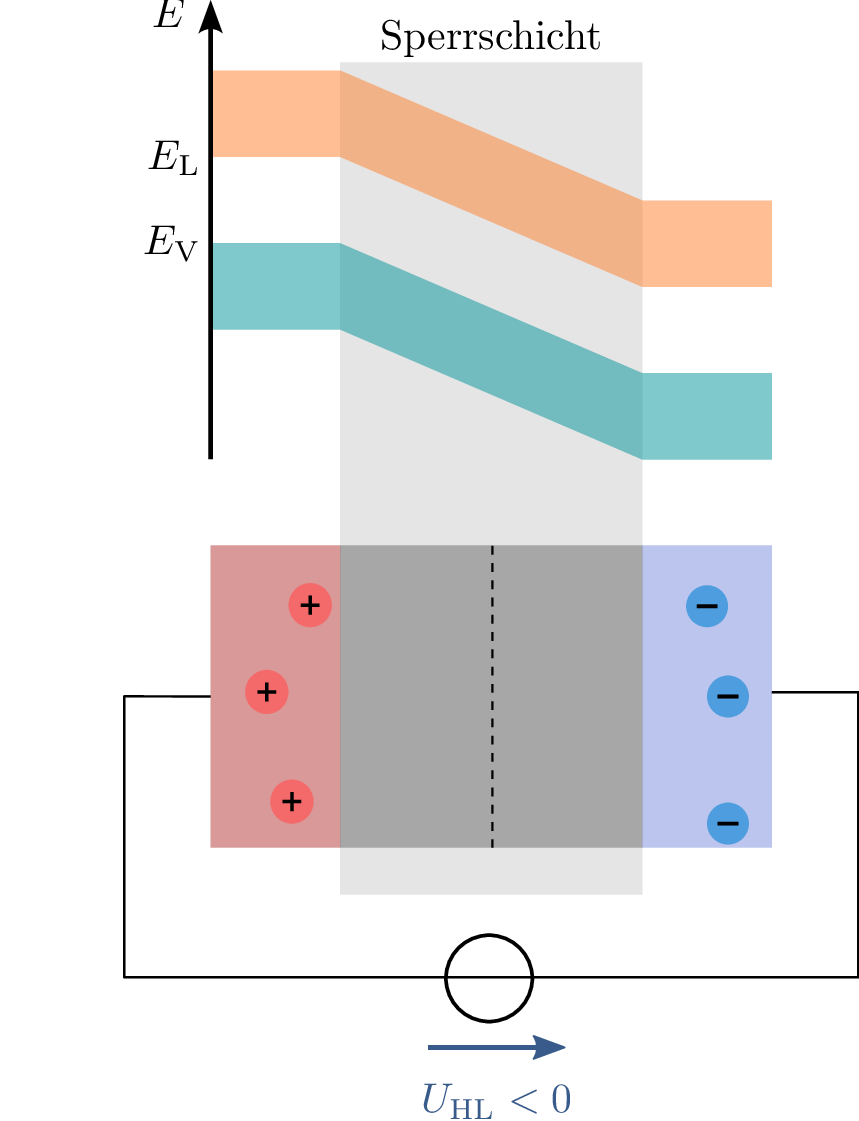
Wenn eine Spannung in Durchlassrichtung angelegt wird (siehe Abbildung 15 links), wird die RLZ verkleinert und der Übergang wird leitend. Elektronen aus der n-dotierten Seite wandern zur p-dotierten Seite, während Löcher von der p-dotierten Seite zur n-dotierten Seite diffundieren. Dadurch entsteht ein Stromfluss durch den pn-Übergang. Andersherum vergrößert eine Spannung entgegen der Durchlassrichtung die RLZ (siehe Abbildung 15 rechts). Die freien Ladungsträger werden durch die Spannungsquelle ausgeglichen. Der pn-Übergang ist daher ein Schlüsselelement in Halbleiterbauelementen, das die Richtung und Stärke des Stromflusses steuert. Seine Eigenschaften werden durch die Dotierungskonzentration, die Größe der Raumladungszone und die angelegte Spannung beeinflusst.
Merke:
- Der pn-Übergang kombiniert eine p- und n-dotierte Halbleiterschicht.
- Im Übergangsbereich, Raumladungszone genannt, sind keine freien Ladungsträger.
- In Durchlassrichtung wird die RLZ verkleinert, in Sperrrichtung wird diese vergrößert.