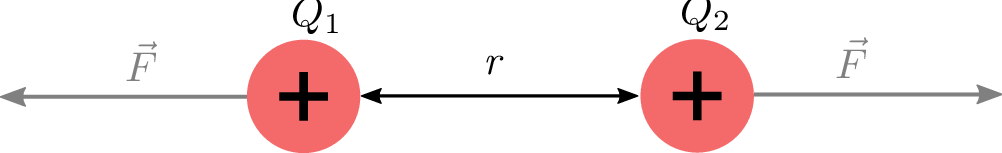Die elektrische Ladung

1 Der Atomaufbau

Viele physikalische Prozesse sind nur durch klassische Phönomene aus der Mechanik nicht zu erklären. Bereits etwa 600 v. Chr. entdeckte der griechische Philosoph Thales von Milet, dass Bernstein, wenn er an einem Fell gerieben wird, leichte Objekte wie Federn anzieht. In weiteren Experimenten konnte bedeutend später nachgewiesen werden, dass es neben der Gravitationskraft eine weitere, sogenannte elektrische Kraft gibt. Diese kann sowohl anziehend als auch abstoßend wirken. Als Ursache dieser Kraftwirkungen werden elektrische Ladungen postuliert und als (historisch willkürlich) positiv und negativ festgelegt. Gleichnamige Ladungen stoßen sich ab, ungleichnamige Ladungen hingegen ziehen sich an.

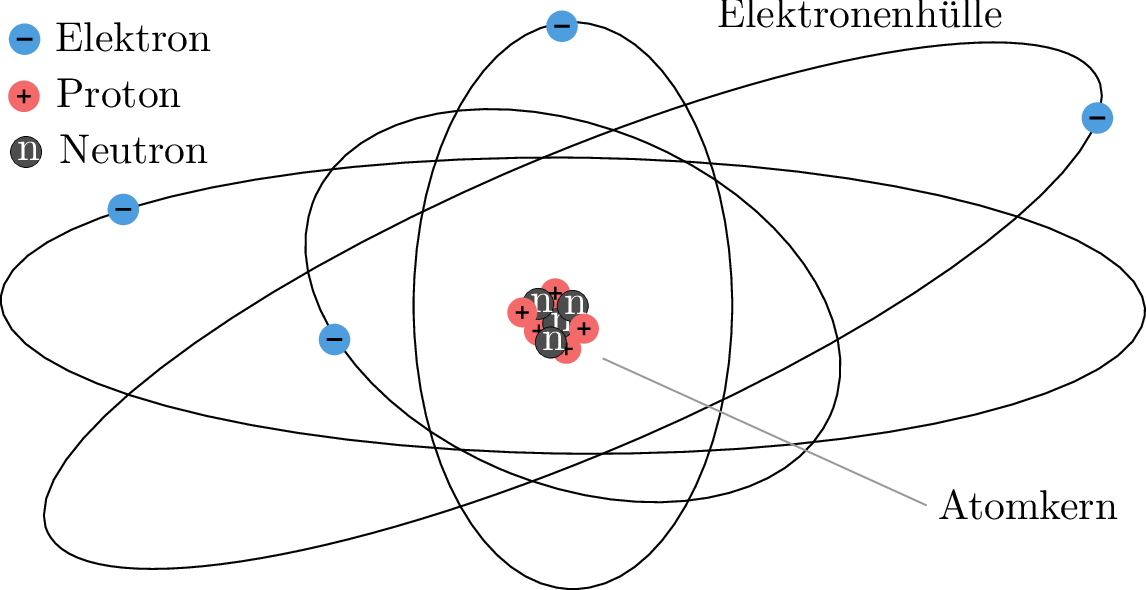
Eine einfache, den beobachteten Effekten zu Grunde liegende Modellvorstellung entwickelte Nils Bohr 1913. Laut diesem in Abbildung 1 dargestellten Atommodell besteht jedes Atom aus einen Atomkern und einer Elektronenhülle. Der Atomkern wiederum besteht aus dicht gepackten Protonen (positive Ladungsträger) und Neutronen (elektrisch neutral). Die Hülle besteht aus Elektronen (negative Ladungsträger), die den Atomkern auf konzentrischen Bahnen mit unterschiedlichen Radien umkreisen.

Die Ladung \(Q\) eines Protons und eines Elektrons ist betragsmäßig gleich und wird als Elementarladung \(e\) bezeichnet. Ihr experimentell bestimmter Wert beträgt \(e = 1,6 \cdot 10^{-19} \, \mathrm {C}\). Das Proton ist positiv und das Elektron negativ geladen. Ein Atom hat im Regelfall die identische Anzahl Protonen wie Elektronen und ist daher von außen gesehen elektrisch neutral.

Das Coulomb ist die Einheit der elektrischen Ladung und wird wie folgt beschrieben:

\begin {equation*} \mathit {[Q]} = \rm { 1 \, Coulomb = 1 \, C = 1 \, As} \end {equation*}

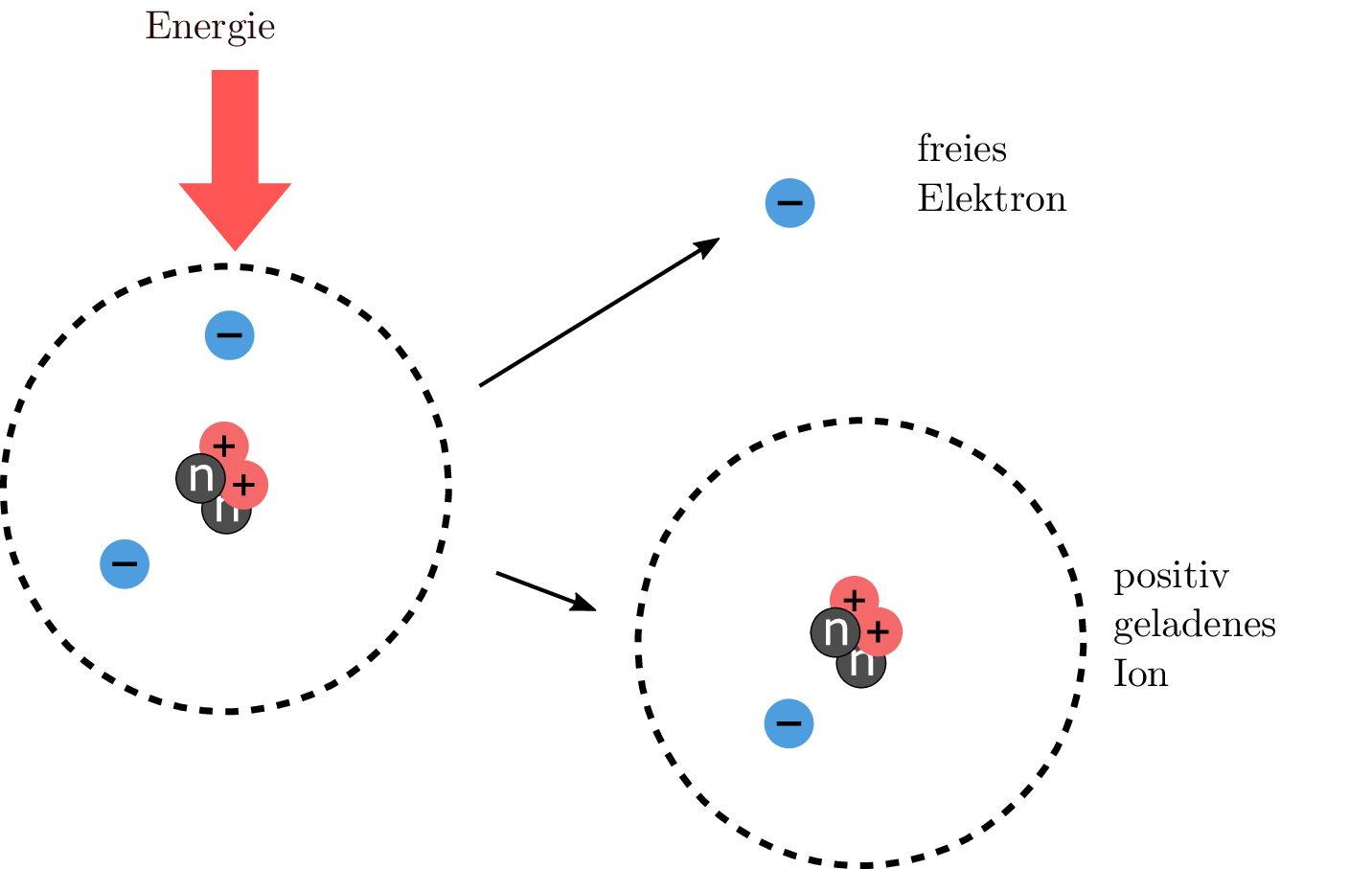
Durch Zufuhr von Energie oder durch Wechselwirkung mit anderen Teilchen (beispielsweise durch Reibung eines Plastikstabes an einem Stück Stoff, Reibung von Kleidung an einer Kunststoffrutsche, UV-Strahlung) kann sich die Elektronenanzahl eines Atoms verändern. Bekommt ein Atom ein oder mehrere zusätzliche Elektronen, liegt also ein Elektronenüberschuss vor, wird es negativ geladen. Verliert es Elektronen, also bei einem Elektronenmangel, wird es positiv geladen. In beiden Fällen wird es als Ion bezeichnet. Da jeweils nur ganze Elektronen dem Ion hinzugefügt oder abgezogen werden können, ist die entsprechende Ladung \(Q\) eines Ions (und damit auch jedes anderen Objektes) immer ein Vielfaches der Elementarladung \(e\).

Die Masse der sich im Kern befindenden Protonen und Neutronen ist um viele Größenordnungen höher als die der Elektronen. Folglich sind die aus dem Atomverband befreiten Elektronen als kleinste, leichteste und beweglichste Ladungsträger für die Elektrotechnik von großer Bedeutung.

2 Ladungsdichten

Nicht nur die Anzahl, sondern auch die Verteilung der elektrischen Ladungsträger spielt in der Elektrotechnik eine wichtige Rolle. So ist es beispielsweise für die Gestaltung und Funktionsweise von elektrischen Bauelemente (wie Widerständen, Kondensatoren oder Halbleiterbauelementen) entscheidend zu wissen, wie sich die Ladungen entlang von Linien, auf Oberflächen oder innerhalb von Volumina verteilen. Dabei wird in diesem Modul von einer gleichmäßigen Ladungsträgerverteilung ausgegangen.

Die Punktladung dient als idealisiertes Modell einer Ladungsverteilung auf einen Punkt ohne räumliche Ausdehnung. Ist die reale räumliche Verteilung an der entsprechenden Stelle nicht weiter relevant, werden Ladungen meist als Punktladungen betrachtet.

Die Linienladungsdichte \(\lambda \) (lambda), angegeben in C/m, beschreibt die Verteilung der elektrischen Ladung entlang einer Linie, wie sie beispielsweise in einem sehr dünnen Draht vorkommt, der nur in einer Dimension ausgedehnt ist (siehe Abbildung 3).

Da die Ladungsträger sowie ihre atomaren Strukturen im Vergleich zu den in Bauteilen verwendeten Strukturen vernachlässigbar klein sind, kann statt der diskreten eine kontinuierliche Verteilung angenommen werden. Folglich lässt sich die Linienladungsdichte als Ableitung der Ladung pro Linienlänge beschreiben.

\begin {equation*} \lambda = \lim \limits _{l \to 0} \frac {\Delta Q}{\Delta l} = \frac {\mathrm {d}Q}{\mathrm {d}l} \end {equation*}

Die Ladung \(Q\) ist analog dazu das Integral der Linienladungsdichte \(\lambda \) über die Länge \(l\).

\begin {equation*} Q = \int \limits _l \lambda \, \mathrm {d}l \end {equation*}

Die Flächenladungsdichte \(\sigma \) (sigma) in \(\mathrm {C/m^2}\) beschreibt die Verteilung der Ladung \(Q\), die pro Flächeneinheit \(A\) verteilt ist (siehe Abbildung 4). Sie wird beispielsweise bei der Berechnung von Kondensatoren, welche zu einem späteren Zeitpunkt eingeführt werden, benötigt.

Vergleichbar zur Linienladungsdichte kann auch \(\sigma \) über eine Grenzwertbetrachtung und damit über eine Ableitung beschrieben werden:

\begin {equation*} \sigma = \lim \limits _{A \to 0} \frac {\Delta Q}{\Delta A} = \frac {\mathrm {d}Q}{\mathrm {d}A} \end {equation*}

\begin {equation*} Q = \iint \limits _A \sigma \, \mathrm {d}A \end {equation*}

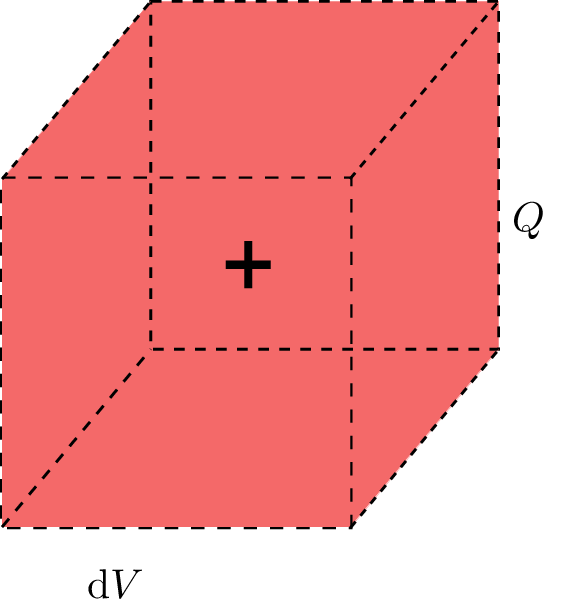
Die Raumladungsdichte \(\rho \) (rho) in \(\mathrm {C/m^3}\) gibt die Anzahl der freien Ladungsträger im betrachteten Volumen an. Hierbei kann es sich beispielsweise um Elektronen in einem Leiter oder geladene Ionen in einem Gasgemisch handeln.

\begin {equation*} \rho = \lim \limits _{V \to \infty } \frac {\Delta Q}{\Delta V} = \frac {\mathrm {d}Q}{\mathrm {d}V} \end {equation*} \begin {equation*} Q = \iiint \limits _V \rho \, \mathrm {d}V \end {equation*}

3 Elektrische Leiter - Metalle

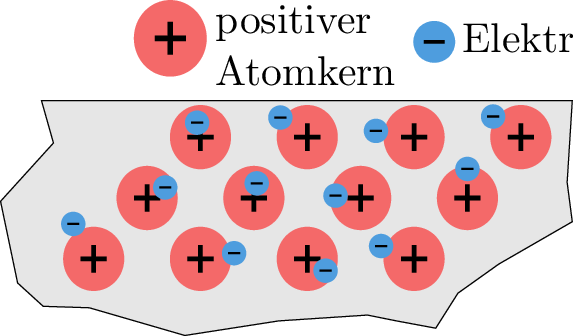
Diese Aufteilung der Ladungsträger ist beispielsweise in Metallen gut zu sehen. Viele Metalle weisen einen besonderen Atomverband auf. Die Atome ordnen sich bei ihnen in einer regelmäßigen Gitterstruktur an. Dadurch sind die äußersten Elektronen eines jeden Atoms innerhalb des Metallkörpers nahezu frei beweglich. Diese freien Elektronen verleihen Metallen ihre elektrisch leitende Eigenschaft. In Abbildung 6 wird diese Struktur dargestellt. Häufig werden Metalle in der Elektrotechnik deshalb kurz als (elektrische) Leiter bezeichnet. Im Allgemeinen sind Leiter elektrisch neutral, da in jedem Atom die Summe aller Elektronen der Summe aller Protonen entspricht.

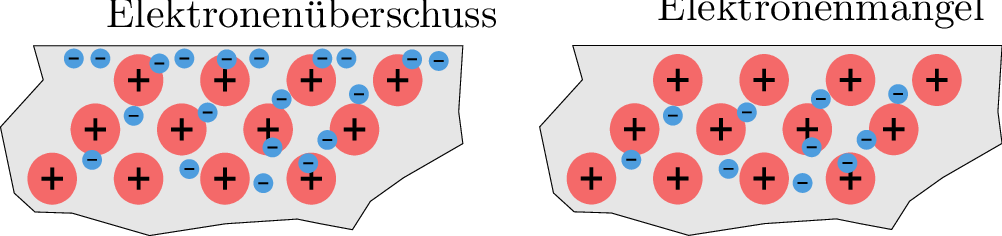
Durch das Hinzuführen von Elektronen entsteht ein Elektronenüberschuss, wodurch der Leiter negativ geladen wird. Werden Elektronen entzogen entsteht ein Elektronenmangel und der Leiter wird positiv geladen (Abbildung 7).

4 Das Coulombsche Gesetz

Geladene Teilchen beeinflussen sich gegenseitig, wobei sich Ladungen gleichen Vorzeichens abstoßen und unterschiedlichen Vorzeichens anziehen. Bereits um 1785 konnte Charles Augustin de Coulomb experimentell nachweisen, dass sich der Betrag der Kraft proportional zu jeder der kugelsymmetrischen Ladungen \(Q_1\) und \(Q_2\), aber antiproportional zum Quadrat des Abstandes \(r\) der beiden Ladungen voneinander verhält.

Die proportionale Wechselwirkung zwischen den Ladungen \(Q_1\) sowie \(Q_2\) und dem Abstandsquadrat \(r^2\) führt mit der Proportionalitätskonstante \(\frac {1}{4 \pi \varepsilon _0}\) zur Kraft zwischen den Ladungen. Dieser proportionale Zusammenhang ist in Abbildung 8 dargestellt.

Durch das Einführen eines Proportionalitätstermes kann aus dem zuvor bestimmten proportionalen Zusammenhang die resultierende Kraft \(F\) direkt errechnet werden. Die resultierende Gleichung 1 wird Coulombsches Gesetz genannt.

\begin {equation} F \sim \frac {Q_1 Q_2}{r^2} \rightarrow F = \frac {1}{4 \pi \varepsilon _0} \frac {Q_1 Q_2}{r^2} \label {eq:coulomb} \end {equation}

Der Faktor \(\varepsilon _0\) wird als elektrische Feldkonstante (auch Dielektrizitätskonstante des Vakuums) bezeichnet, während die 4 \(\pi \) ihren Ursprung in geometrischen Betrachutngen der Anordnung haben.

Der Wert der elektrischen Feldkonstante beträgt etwa:

\begin {equation*} \varepsilon _0 = 8,854 \cdot 10^{-12} \rm {As/Vm} \end {equation*}

Gibt es mehr als zwei Ladungen, kann die resultierende Kraft auf jede der einzelnen Ladungen durch die Addition aller Einzelkräfte errechnet werden, die sich aus jeder Zweierkombination von Ladungen ergibt, an der die Zielladung beteiligt ist. Dieser Effekt wird als Superpositionsprinzip bezeichnet, welches auch im Modul 5 Erweiterte Gleichstromnetzwerke zur Berechnung von sich ergebenden Spannungen verwendet wird.

In der Praxis wird dieser Effekt unter anderem beim elektrostatischen Aufspannen von Papier auf Plottern, bei Laserdruckern zur Übertragung des Tonerpulvers auf das Papier, bei Touchscreens zur Bestimmung des Berührungspunktes oder bei Plasmabildschirmen zur kontrollierten Gasentladung von Ionen zur Lichterzeugung genutzt.