Das elektrische Feld

1 Charakterisierung des elektrischen Feldes

Wie gezeigt haben elektrische Ladungen einen direkten Einfluss auf andere Ladungen. Dies geschieht dadurch, dass sie die Eigenschaften des Raums um sich herum verändern. Diese Veränderungen können durch ein Feldmodell beschrieben werden. Der Feldbegriff ist in der Physik von fundamentaler Bedeutung. Beispiele hierfür sind das Temperaturfeld, in dem die Temperatur abhängig von seinem Ort durch eine skalare Größe beschrieben wird. Neben solchen skalaren Feldern gibt es auch Vektorfelder, in denen jedem Ort neben einer Größe auch eine Richtung, in die sie wirkt, zugeschrieben wird. Beispiele hierfür sind das Gravitationsfeld oder ein Strömungsfeld, welches beispielsweise die Richtung und Geschwindigkeit von Wasserteilchen beschreibt.

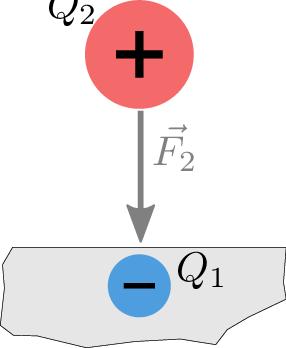
Das elektrische Feld wird durch Größe (in Newton) sowie die Richtung der Kraft \(\vec {F_\mathrm {E}}\) auf eine positive Probeladung \(Q_2\) beschrieben und durch Feldlinien charakterisiert. Dargestellt wird diese Anordnung in Abbildung 1.

Die elektrische Feldstärke ist also:

\begin {equation} \vec {E_1} = \frac {\vec {F_2}}{Q_2} \left [ \frac {\mathrm {N}}{\mathrm {C}} = \frac {\frac {\mathrm {kg \cdot m}}{\mathrm {s}}}{\mathrm {A \cdot s}} = \frac {\mathrm {V}}{\mathrm {m}} \right ] \label {eq:e_feld} \end {equation}

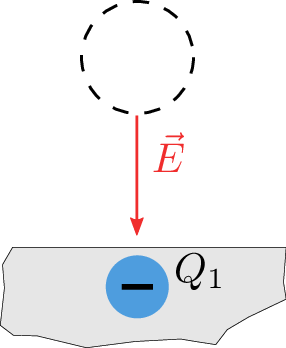
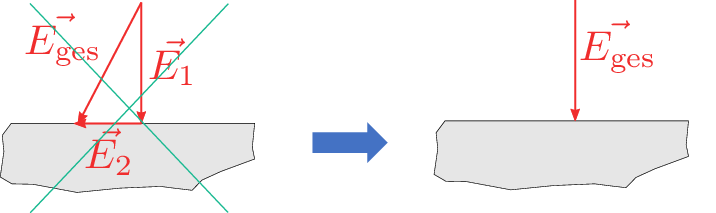
Nachteilig an dieser Definition erscheint auf den ersten Blick, dass die elektrische Feldstärke von der Probeladung \(Q_2\) abhängig zu sein scheint. Durch Einsetzen des Coulombschen Gesetzes (Gleichung ??) in Gleichung 1 lässt sich jedoch zeigen, dass die Kraft \(F_2\) immer proportional zur Probeladung \(Q_2\) steigt. Ihr Verhältnis liefert also immer den gleichen Betrag für die elektrische Feldstärke, und diese wird, wie in Abbildung 2 gezeigt, unabhängig von der Probeladung:

\begin {equation} \vec {E_1} = \frac {\vec {F_2}}{Q_2} =\frac {1}{4 \pi \varepsilon _0} \cdot \frac {Q_1 \cdot Q_2}{r^2} \cdot \frac {1}{Q_2} = \frac {1}{4 \pi \varepsilon _0} \cdot \frac {Q_1}{r^2} \label {e_feld2} \end {equation}

2 Elektrische Leiter und elektrostatische Felder I

Im vorherigen Kapitel wird die Wirkung von Punktladungen auf das elektrische Feld untersucht. Da im Alltag elektrische Felder jedoch häufig von geladenen, elektrischen Leitern (wie Metallen) ausgehen, werden sie hier gesondert aufgeführt.

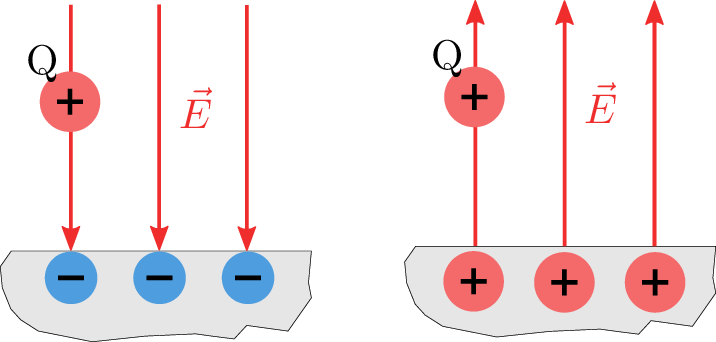
Liegt ein Elektronenüberschuss vor, wird - wie in Abbildung ?? dargestellt - die positive Probeladung \(Q\) in Richtung der Plattenoberflächen angezogen. Auch die Feldlinien \(\vec {E}\) des elektrischen Feldes verlaufen in Richtung der Leiteroberfläche. Im Falle eines Elektronenmangels wird die Probeladung abgestoßen, auch die Feldlinien führen vom positiven Leiter weg.

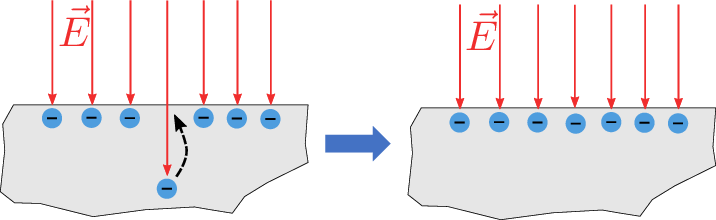
Da die Elektronen innerhalb eines Leiters frei beweglich sind, würden diese im Falle eines elektrischen Feldes innerhalb eines Leiters durch dieses Feld angezogen (oder abgestoßen) werden, bis sich das Feld innerhalb des Leiters ausgeglichen hat (siehe Abbildung 4). Folglich kann in diesem Fall kein elektrisches Feld innerhalb eines Leiters existieren

Dies führt zu der Erkenntnis, dass die elektrischen Feldlinien zwangsläufig senkrecht auf der Oberfläche von Leitern stehen müssen (siehe Abbildung 5). Eine schräg stehende Feldlinie ließe sich sonst vektoriell in eine senkrecht und eine horizontal auf der Leiteroberfläche verlaufende Komponente zerlegen. Da diese horizontale Komponente augenblicklich durch die sich bewegenden Ladungsträger ausgleichen wird, kann sie nicht existieren. Dieser Effekt tritt ausschließlich bei elektrisch leitenden Materialien auf, in nicht leitenden Materialien (sogenannten Isolatoren) gibt es keine beweglichen Ladungsträger, welche die horizontale Komponente ausgleichen können.

3 Beispiele elektrischer Felder

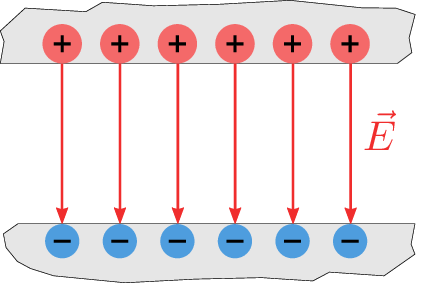
Das einfachste elektrische Feld ist das Homogenfeld. In diesem Feld sind sowohl der Betrag als auch die Richtung der elektrischen Feldstärke \(\vec {E}\) an jedem Punkt konstant. Eine sich in diesem Feld befindliche Probeladung erfährt also an jeder Stelle die gleiche Kraftwirkung. Erzeugen lässt sich ein solches Feld wie in Abbildung 6 dargestellt beispielsweise zwischen zwei parallelen Metallplatten, welche mit unterschiedlichen Ladungen \(Q\) aufgeladen sind. Die Feldlinien verlaufen grundsätzlich von der positiv aufgeladenen zur negativ aufgeladenen Metallplatte. Häufig wird die Dichte, in der die Feldlinien eingezeichnet sind, als Maß für die Stärke des elektrischen Feldes verwendet. Je dichter die Feldlinien eingezeichnet sind, desto stärker ist das elektrische Feld an dieser Stelle.

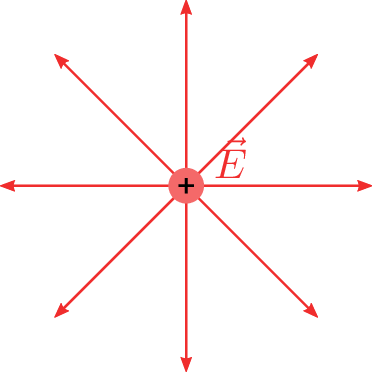
Das elektrische Feld einer Punktladung wird auch als Radialfeld (siehe Abbildung 7) bezeichnet. Unter der idealisierten Annahme, dass sich unendlich weit entfert eine Hülle mit entgegengesetzter Ladung befindet, breiten sich die Feldlinien geradelinig aus. In ihrer symmetrischen Anordnung zeigen sie bei positiven Punktladungen in Richtung der negativen Hülle, bei negativen Punktladungen in Richtung der Punktladung.

Die elektrische Feldstärke \(\vec {E}\) ist direkt proportional zur Ladung \(Q\), verringert sich jedoch mit zunehmendem Abstand \(r\) von ihr quadratisch. Errechnet werden kann ihr Betrag über:

\begin {equation} E = \frac {1}{4 \pi \varepsilon _0} \frac {Q}{r^2} \end {equation}

Die mit zunehmendem Abstand \(r\) von der Punktladung schwächer werdende elektrische Feldstärke zeigt sich neben dem mathematischen Zusammenhang auch in dem größer werdenden Abstand zwischen den Feldlinien.

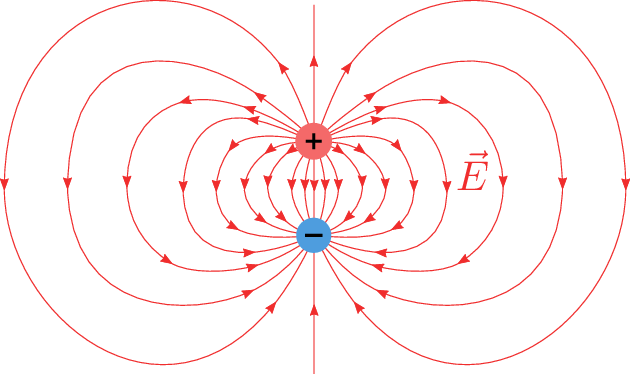
Kompliziertere elektrische Felder ergeben sich schon beim Hinzufügen einer zweiten Punktladung. Im Fall von zwei betragsgleichen Ladungen unterschiedlichen Vorzeichens (Abbildung 8) ergibt sich zwischen den Ladungen ein nahezu gleichmäßiges Feld, während es weiter außen bedeutend schwächer wird.

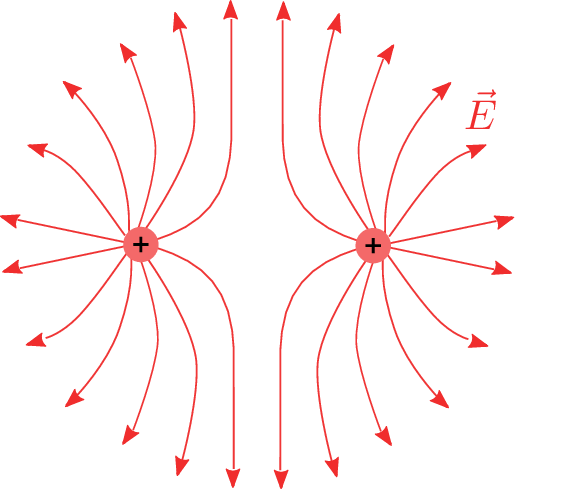
Der Fall mit zwei identischen Punktladungen zeigt wie in Abbildung 9 eine Besonderheit des elektrischen Feldes. Während sich die Feldlinien im Rest des Raumes erwartbar von den positiven Ladungen wegzeigen, gibt es zwischen den Punktladungen einen freien Raum ohne Feldlinien. Dies liegt daran, dass sich die entgegengesetzten Feldlinien in diesem Zwischenraum gegenseitig kompensieren. Im Punkt zwischen beiden Ladungen liegt keine elektrische Feldstärke vor, auf der Ebene zwischen den Ladungen neutralisieren sich die jeweiligen horizontalen Kompenenten, und es liegt lediglich ein elektrisches Feld in der jeweiligen vertikalen Richtung vor.