Die elektrische Stromstärke
Lernziele: Die Elektrische Stromstärke
Die Studierenden können
- die Begriffe der elektrischen Stromstärke und der elektrischen Stromdichte erläutern und anwenden
- die elektrische Stromstärke sowie die elektrische Stromdichte in einfachen Anordnungen berechnen
- die Driftgeschwindigkeit von Elektronen in einfachen Anordnungen bestimmen
1 Das elektrische Strömungsfeld
Die vorherigen Kapitel beziehen sich ausschließlich auf ruhende Ladungsträger. Folglich wird dieser Teilbereich der Elektrotechnik als Elektrostatik bezeichnet.
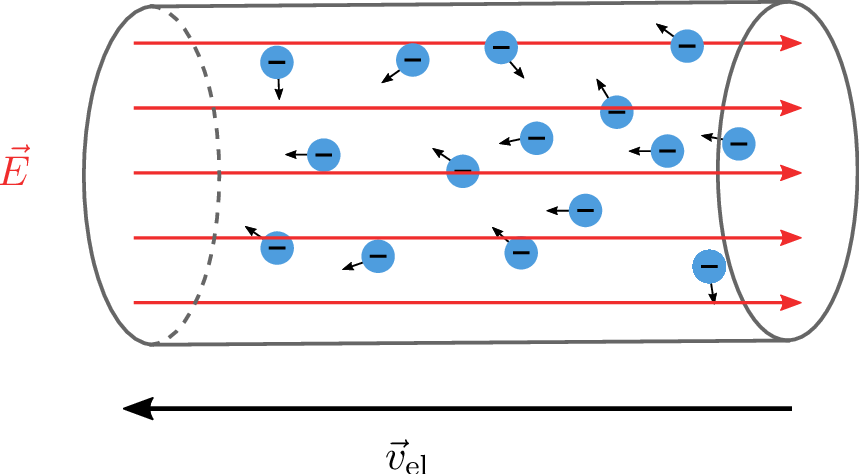
Auf molekularer Ebene bewegen sich die freien Elektronen in einem elektrischen Leiter ständig in zufällige Richtungen. Im Mittel gleicht sich die Bewegung der einzelnen Elektronen jedoch aus. Liegt an einem Leiter ein elektrisches Feld \(\vec {E}\) an, so werden die frei beweglichen Elektronen in diesem in Richtung der positiv geladenen Elektrode angezogen (siehe Abbildung 1). Zusätzlich zur zufälligen, ungerichteten Bewegung wird eine gerichtete Bewegungskomponente hinzugefügt. Liegt eine solche gerichtete Bewegung von Teilchen vor, wird von einem Strömungsfeld gesprochen.
Neben Elektronen in Leitern kann ein elektrisches Strömungsfeld auch durch geladene Ionen in Gasen oder Flüssigkeiten hervorgerufen werden.
Im Fall einer im zeitlichen Mittel konstanten Ladungsträgerbewegung, was im abgebildeten Leiter durch ein konstantes elektrisches Feld erreicht wird, liegt ein stationäres elektrisches Strömungsfeld vor.
2 Der elektrische Strom
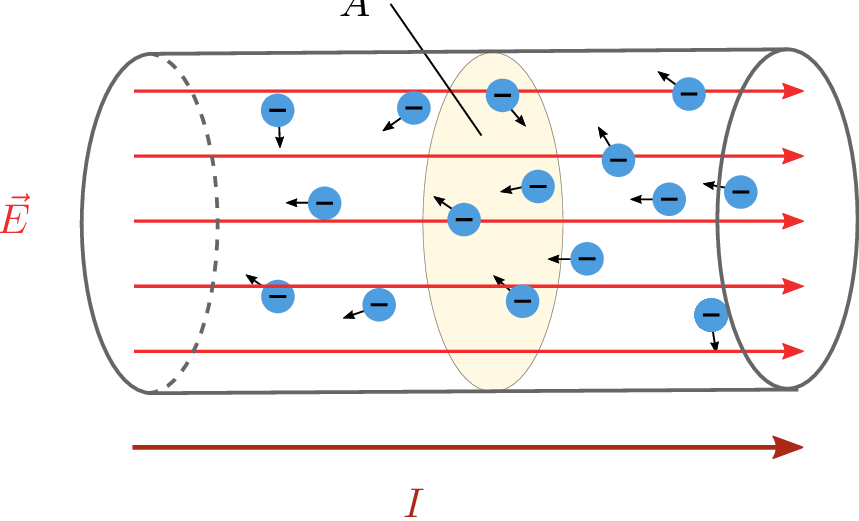
Als elektrische Stromstärke \(I\) wird die gerichtete Bewegung (Driftbewegung) von elektrischen Ladungsträgern bezeichnet. Die Richtung der elektrischen Stromstärke ist so definiert, dass sie vom höheren Potential (positiv geladene Elektrode) zum niedrigeren Potential verläuft. Damit verläuft sie in die gleiche Richtung wie die elektrische Feldstärke, jedoch in die zur Driftgeschwindigkeit der Elektronen entgegengesetzen Richtung (siehe Abbildung 2).
Die Elektronen erreichen eine feldstärkeabhängige Driftgeschwindigkeit \(\vec {v}_\mathrm {el}\). Zusammenstöße mit den Metallatomen aus der Gitterstruktur behindern die freie Bewegung der Elektronen, und wirken dieser als eine Art Widerstand entgegen.
\begin {equation} \vec {v}_\mathrm {el} = - b_\mathrm {el} \cdot \vec {E} \label {eq:driftgeschw} \end {equation}
\begin {equation*} [ \vec {v}_\mathrm {el} ] = \frac {\mathrm {m}}{\mathrm {s}} \end {equation*}
Der Proportionalitätsfaktor \(b_\mathrm {el}\) zwischen der Driftgeschwindigkeit \(\vec {v}_\mathrm {el}\) und der elektrischen Feldstärke \(\vec {E}\) wird als Elektronenbeweglichkeit bezeichnet.
\begin {equation*} [b_\mathrm {el}] = \frac {\mathrm {m}^2}{\mathrm {Vs}} \end {equation*}
Neben der Driftgeschwindigkeit \(\vec {v}_\mathrm {el}\) ist auch die Anzahl der Elektronen \(N_\mathrm {el}\) sowie deren Ladungsmenge \(\Delta Q\) zur Ermittlung der elektrischen Stromstärke \(I\) relevant.
Die Ladungsmenge \(\Delta Q\) entspricht
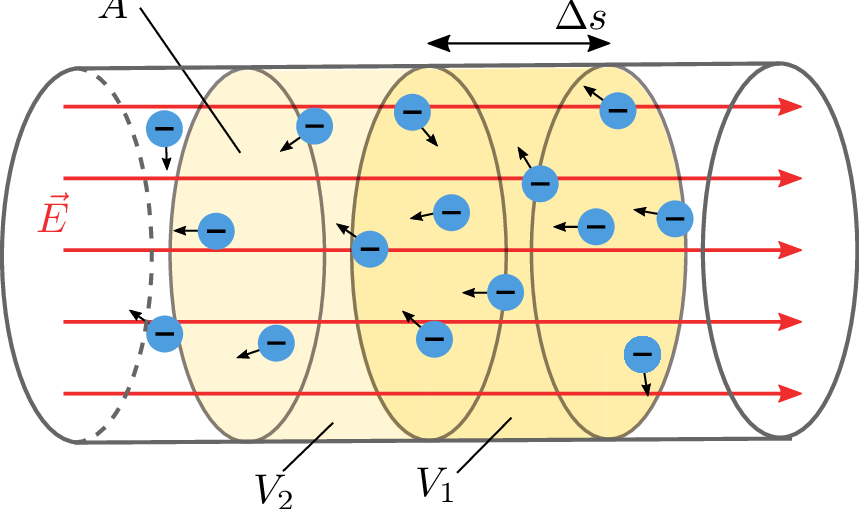
\begin {equation*} \Delta Q = e \cdot N_\mathrm {el} = e \cdot n_\mathrm {el} \cdot V_1 \, \end {equation*}
wobei \(n_\mathrm {el}\) die Dichte der Ladungsträger im Volumen \(V_1\) angibt.
Mit \(V_1 = \Delta s \cdot A\) und \(\Delta s = v_\mathrm {el} \cdot \Delta t\) ergibt sich:
\begin {equation*} \Delta Q = e \cdot n_\mathrm {el} \cdot v_\mathrm {el} \cdot \Delta t \cdot A \end {equation*}
Über die Definition der Driftgeschwindigkeit (1) führt dies zu:
\begin {equation*} \Delta Q = e \cdot n_\mathrm {el} \cdot b_\mathrm {el} \cdot E \cdot \Delta t \cdot A \, , \end {equation*}
woraus sich die Änderung der Ladungsmenge \(\Delta Q\) pro Zeiteinheit \(\Delta t\) herleiten lässt:
\begin {equation*} \frac {\Delta Q}{\Delta t} = e \cdot n_\mathrm {el} \cdot b_\mathrm {el} \cdot E \cdot A \end {equation*}
3 Definition der elektrischen Stromstärke
Diese so ermittelte Ladungsänderung über die Zeit wird als elektrische Stromstärke \(I\) bezeichnet:
\begin {equation} I = \frac {\Delta Q}{\Delta t} \label {eq:stromdef} \end {equation}
\begin {equation*} [I] = \mathrm {Ampere} = \mathrm {A} \end {equation*}
Aus dieser Definition der Stromstärke folgt, dass eine über einen Zeitraum aufaddierte elektrische Stromstärke die in dieser Zeit transporte Ladungsmenge \(Q\) ergibt:
\begin {equation} Q = \int _{t_1}^{t_2} i(t) \, \mathrm {d} t \end {equation} Neben der gesamten elektrischen Stromstärke \(I\) ist oft auch der auf den Leiterquerschnitt bezogene Strom von Interesse. Zur Berechnung dieser Stromdichte \(J\) wird die Stromstärke \(\Delta I\) durch ein elementar kleines Flächenelement \(\Delta A\) betrachtet:
\begin {equation} J = \frac {\Delta I}{\Delta A} \end {equation}
Ist die elektrische Stromstärke \(I\) über eine Fläche gleichmäßig verteilt, lässt sich dies vereinfachen:
\begin {equation} J = \frac {I}{A} \end {equation}
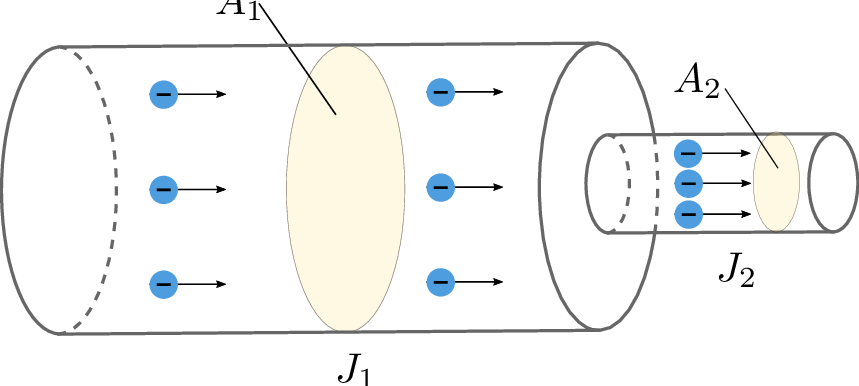
Da die Stromstärke \(I\) über den gesamten Leiter hinweg identisch bleibt, ändert sich bei einer Querschnittsverkleinerung des Leiters auch die resultierende elektrische Stromdichte \(J\) (siehe Abbildung 4).
Hier gilt:
\begin {equation*} J_1 \cdot A_1 = J_2 \cdot A_2 = I \end {equation*}
Beispiel 1
Durch eine Kupferleitung mit dem Querschnitt \(A = 1 \mathrm {mm}^2\) fließt ein Strom von \(I = 8 \mathrm {A}\). Ein \(\mathrm {mm}^3\) enthält etwa \( 8,5 \cdot 10^{19}\) Atome. Jeweils 1 Elektron pro Atom sei am Ladungstransport beteiligt.
Mit welcher Driftgeschwindigkeit bewegen sich die Elektronen im Mittel durch die Leitung?
\begin {equation*} \vec {v}_\mathrm {el} = - b_\mathrm {el} \cdot \vec {E} \end {equation*}
Da sich die negativ geladenen Elektronen entgegen der Feldrichtung \(\vec {E}\) (und somit auch entgegen der technischen Stromrichtung \(I\)) bewegen, ist die Richtung der Driftgeschwindigkeit ausreichend beschrieben, und es genügt, den Betrag \(v_\mathrm {el}\) zu berechen.
mit dem Zusammenhang
\begin {equation*} I = e \cdot n_\mathrm {el} \cdot b_\mathrm {el} \cdot E \cdot A\\ \rightarrow E = \frac {I}{e \cdot n_\mathrm {el} \cdot b_\mathrm {el} \cdot A} \end {equation*}
ergibt sich:
\begin {equation*} v_\mathrm {el} = \cancel {b_\mathrm {el}} \cdot \frac {I}{e \cdot n_\mathrm {el} \cdot \cancel {b_\mathrm {el}} \cdot A} \end {equation*}
Einsetzen der Zahlenwerte:
\begin {equation*} v_\mathrm {el} = \frac {8 \mathrm {A}}{1,602 \cdot 10^{-19} \, \mathrm {As} \cdot 8,5 \cdot 10^{19} \, \mathrm {mm}^{-3} \cdot 1 \, \mathrm {mm}^2 } \end {equation*}
\begin {equation*} v_\mathrm {el} = 0,59 \frac {\mathrm {mm}}{s} \end {equation*}
Die Elektronen bewegen sich im Mittel also mit 0,59 mm/s. Da sich innerhalb des Leiters die elektrische Feldstärke jedoch mit Lichtgeschwindigkeit fortbewegt, setzen sich alle Elektronen des Leiters praktisch gleichzeitig in Bewegen. Vergleichbar ist dies mit einem vollständig mit Murmeln gefüllten Rohr. Im Moment des hereinschiebens einer weiteren Murmel fällt auf der anderen Seite eine Murmel heraus, obwohl sich die einzelnen Murmeln nur langsam bewegen.