Die Arbeit

In diesem Kapitel wird zur Unterscheidung zwischen Arbeit und Energie das Symbol \(E\) für Energie (ohne Vektorpfeil) und \(W\) für Arbeit (vom englischen Wort ”work”) verwendet. Obwohl das Formelzeichen \(W\) umgangssprachlich häufig sowohl für Arbeit als auch für Energie benutzt wird, ist Arbeit im Wesentlichen eine Veränderung der Energie. Beide Größen, Arbeit und Energie, werden in der Einheit Joule (J) gemessen. Wie im Abschnitt über die Energieerhaltung beschrieben, besagt der Energieerhaltungssatz, dass Energie weder erzeugt noch vernichtet werden kann. Sie ändert lediglich ihre Form. Diesen Zusammenhang beschreibt die folgende Formel:

\begin {equation} W = \Delta E \quad \quad [W] = \text {1 Joule = 1 J = 1 Nm} \end {equation}

Diese Änderung der Energiemenge kann durch verschiedene physikalische Aktionen hervorgerufen werden, einschließlich der Verschiebung eines Objekts in einem Kraftfeld. Um diese Konzepte weiter zu veranschaulichen, ist im Folgenden die allgemeine Formel 2 für die Arbeit dargestellt:

\begin {equation} W = - \int _{P_\mathrm {1}}^{P_\mathrm {2}} \vec {F} \cdot \mathrm {d}\vec {s} \label {eq:WFds} \end {equation}

Die Gleichung berechnet Arbeit durch Integration der Kraft entlang eines Weges, wobei die Kraftausrichtung zur Bewegungsrichtung des Objekts entscheidend ist. Ein Vorzeichenwechsel in der Formel deutet darauf hin, dass Energie aus einem Energiespeicher für Arbeit verwendet wird. Dieses Vorzeichen ist kontextabhängig und ändert sich je nach Perspektive. Wird Energie entnommen, gilt die Arbeit als negativ, da sie von der gespeicherten Gesamtenergie abgezogen wird, was eine Verringerung der Systemenergie signalisiert.

1 Die elektrische Arbeit

In der Elektrostatik sind die Kräfte \(\vec {F}_{\mathrm {el}}\), die zwischen Ladungsträgern \(Q\) und elektrischen Feldern \(\vec {E}\) wirken, zentral. Diese Kräfte entstehen, wenn elektrische Felder auf Ladungsträger wirken. Das elektrische Feld \(\vec {E}\) wird als Kraft pro Ladung definiert und beschreibt, wie groß die Kraft \(\vec {F}_{\mathrm {el}}\) im Verhältnis zur eingebrachten Ladung \(Q\) ist.

\begin {equation} \vec {E} = \frac {\vec {F}_\mathrm {el}}{Q} \quad \Rightarrow \quad \vec {F}_\mathrm {el} = Q \cdot \vec {E} \end {equation}

Wenn nun die Formel für die elektrische Kraft \(\vec {F}_\mathrm {el}\) in die Formel 2 für die allgemeine Arbeit eingesetzt wird, ergibt das die elektrische Arbeit \(W_\mathrm {el}\). Da sich die Ladung \(Q\) über die Strecke \(s\) nicht verändert, kann diese vor das Integral gezogen werden. Da das elektrische Feld \(\vec {E}\) ein Vektor ist und somit einen Betrag und eine Richtung hat, ist das Produkt aus \(\vec {E}\) und \(\mathrm {d}\vec {s}\) in jedem Fall von der gewählten Strecke \(s\) abhängig. Daher muss über das Produkt \(\vec {E}\) und \(\mathrm {d}\vec {s}\) ein Linienintegral gebildet werden.

\begin {equation} W_\mathrm {el} = \int _{P_\mathrm {1}}^{P_\mathrm {2}} - Q \cdot \vec {E} \cdot \mathrm {d}\vec {s} \quad \Rightarrow \quad W_\mathrm {el} = - Q \int _{P_\mathrm {1}}^{P_\mathrm {2}} \vec {E} \cdot \mathrm {d}\vec {s} \end {equation}

Aus Modul 1 ist bekannt, dass das Integral über \(\vec {E} \cdot \mathrm {d}\vec {s}\) im konstanten Fall die Spannung \(U\) ergibt. Für eine verbraucherunabhängige Darstellung wird in der folgenden Formel das negative Vorzeichen weggelassen, sowie für den konstanten Fall durch Einsetzen der Spannung \(U\) vereinfacht dargestellt.

\begin {equation} W_\mathrm {{el}} = Q \int _{P_\mathrm {1}}^{P_\mathrm {2}} \vec {E} \cdot \mathrm {d}\vec {s} \quad \Rightarrow \quad W_\mathrm {{el}} = Q \cdot U\label {eq:WQU} \end {equation}

Da für einen elektrischen Energietransport eine elektrische Stromstärke notwendig ist, kann nun der aus Modul 1 bekannte Zusammenhang zwischen elektrischer Stromstärke \(I\) und der Ladung \(Q\) verwendet und umgestellt werden, um die Ladung \(Q\) in der Formel 5 auszutauschen. Ein konstanter Stromfluss \(I\) ergibt sich aus einer gleichmäßigen Bewegung der Ladungsträger \(Q\) über die Zeit \(t\). In diesem Fall kann auf den Differentialoperator (\(\mathrm {d}\)) verzichtet werden. Durch Umstellung nach \(Q\) ergibt sich folgende Formel:

\begin {equation} I = \frac {\mathrm {d}Q}{\mathrm {d}t} \quad \Rightarrow \quad Q = I \cdot t \end {equation}

Eingesetzt ergibt dies nun folgenden Ausdruck, welcher verdeutlicht, dass das Verrichten oder Aufbringen von Arbeit einen Stromfluss voraussetzt.

\begin {equation} W_\mathrm {{el}} = U \cdot I \cdot t \quad \quad [W_\mathrm {el}] = \text {1 Joule = 1 J = 1 Ws}\label {eq:WUIt} \end {equation}

2 Wegintegral der elektrischen Arbeit

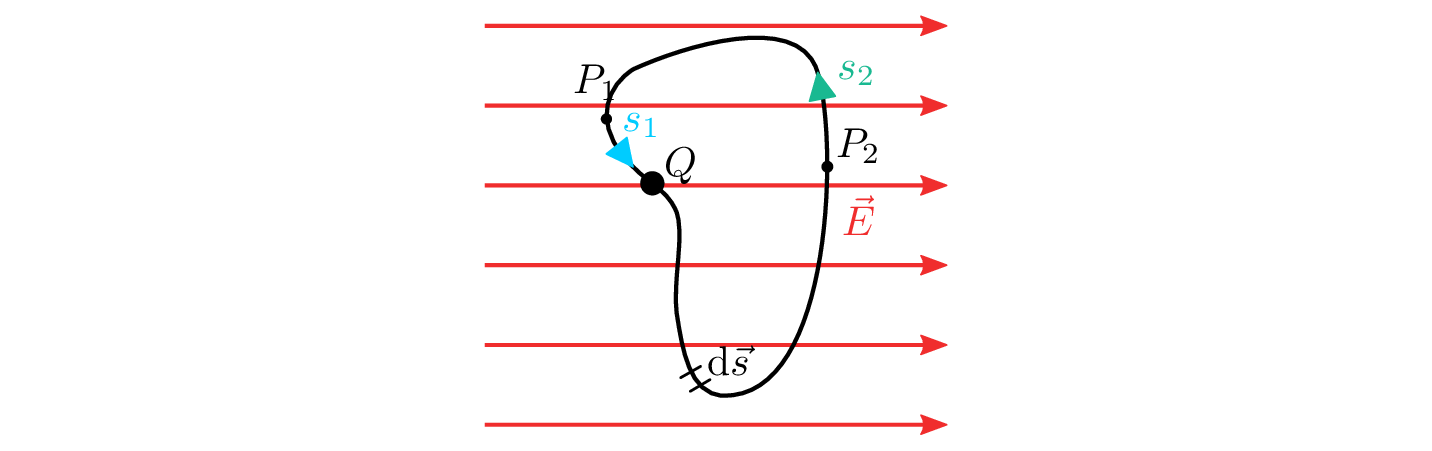
Die Bewegung einer Ladung im elektrischen Feld ist lediglich abhängig von der Positionsänderung entlang der elektrischen Feldlinien. Abhängig von der Bewegungsrichtung entlang oder entgegen der Feldlinien ergibt das entsprechende Vorzeichen. Bewegungen entlang einer Äquipotentialfläche (Fläche mit identischem elektrischen Potential) haben keinen Einfluss auf die elektrische Arbeit. In Abbildung 1 sind die Punkte \(P_\mathrm {1}\) und \(P_\mathrm {2}\) auf je unterschiedlichen Potentialen dargestellt, welche jeweils durch zwei unterschiedliche Strecken \(s_\mathrm {1}\) und \(s_\mathrm {2}\) verbunden sind.

Die Beträge zweier äquidistanter Positionsänderungen in entgegengesetzen Richtungen entlang der elektrischen Feldlinien sind identisch. Diese Eigenschaften führen dazu, dass die Positionsänderung einer Ladung \(Q\) von einem Punkt \(P_\mathrm {1}\) zu einem Punkt \(P_\mathrm {2}\) betragsmäßig gleich einer beliebig anderen Strecke von \(P_\mathrm {2}\) zu \(P_\mathrm {1}\) entspricht.

\begin {equation} \left | W_\mathrm {el} \right | = \left | -Q \cdot \int _{s_\mathrm {1}} \vec {E} \cdot \mathrm {d}\vec {s}\; \right | = \left | -Q \cdot \int _{s_\mathrm {2}}\vec {E} \cdot \mathrm {d}\vec {s}\; \right | \end {equation}

Dieses Verhalten spiegelt wider, dass die Arbeit gleich groß ist, jedoch in einem Fall Arbeit aufgewendet und im anderen Fall Arbeit verrichtet wird. Dies führt zu entgegengesetzten Vorzeichen, was dazu führt, dass sich die Summe beider Arbeiten aufhebt. Mathematisch kann dies auch so ausgedrückt werden, dass das Ringintegral entlang einer beliebigen Kontur zurück zum Ausgangspunkt Null ergibt. Da sich die Ladung \(Q\) außerhalb des Umlaufintegral befindet, ist das Ergebnis somit unabhängig von der Ladungsmenge.

\begin {equation} W_\mathrm {el} = - Q \cdot \int _{s_\mathrm {1}} \vec {E} \cdot \mathrm {d}\vec {s} -Q \cdot \int _{s_\mathrm {2}}\vec {E} \cdot \mathrm {d}\vec {s} = - Q \cdot \oint _{s}\vec {E} \cdot \mathrm {d}\vec {s} = 0 \rightarrow \oint _{s}\vec {E} \cdot \mathrm {d}\vec {s} = 0 \end {equation}

Das Ergebnis des Ringintegrals verdeutlicht ein fundamentales Prinzip der Physik: In einem statischen Feld ist die über einen geschlossenen Weg verrichtete Arbeit immer Null. Dies bestätigt die Wegunabhängigkeit der Arbeit in diesen Feldern und zeigt, dass die verrichtete Arbeit ausschließlich von den Anfangs- und Endpunkten abhängt und nicht vom spezifischen Weg zwischen diesen Punkten.