Der Wirkungsgrad

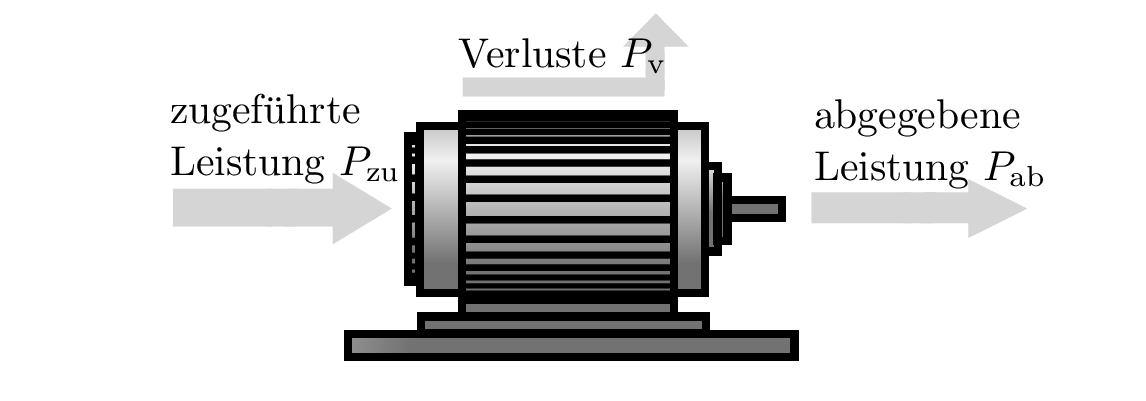
Der Wirkungsgrad beschreibt das Verhältnis von abgegebener Leistung (Nutzleistung) zu aufgenommener Leistung (zugeführte Energie) in einem System und ist ein Maß für die Effizienz, mit der ein System Energie umwandelt. Am Beispiel eines Elektromotors zeigt Abbildung 1 wie sich dessen Leistungsbilanz zusammensetzt.

Der Elektromotor wird am Eingang mit elektrischer Energie versorgt, welche er in einer Eingangsleistung \(P_\mathrm {zu}\) aufnimmt. Die gewünschte Leistung am Ausgang \(P_\mathrm {ab}\) ist in diesem Fall rotatorischer Natur. Die durch den Motor verursachte Abwärme, aber auch die verursachten Geräusche oder Reibung, ergeben zusammen die Verlustleistung \(P_\mathrm {v}\).

1 Berechnung des Wirkungsgrades

Der Wirkungsgrad wird typischerweise als Prozentsatz ausgedrückt. Ein Wirkungsgrad von 100 % bedeutet, dass die gesamte zugeführte Energie effektiv in Nutzenergie umgewandelt wird. Dies ist jedoch in der Praxis aufgrund von Verlusten, meist in Form von Wärme, Reibung oder Schall, nicht erreichbar. Mathematisch wird der Wirkungsgrad \(\eta \) (eta) wie folgt definiert:

\begin {equation} \eta = \frac {P_\mathrm {{ab}}}{P_\mathrm {{zu}}} \cdot 100 \% \end {equation}

Im realen Fall wird der Wirkungsgrad nie 100 % betragen, da eine Energiewandlung grundsätzlich mit Verlusten behaftet ist. Um die Verluste möglichst gering zu halten ist es wichtig sich der Verlustmechanismen bewusst zu werden und diese nach Möglichkeit zu reduzieren. Der nachfolgende Abschnitt erläutert das Prinzip der Verlustmechanismen anhand eines Leuchtmittels.

2 Verlustmechanismen eines Leuchtmittels

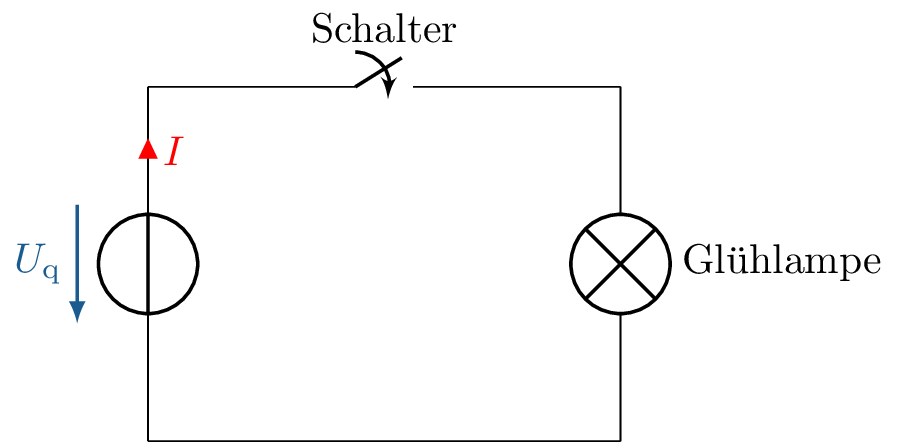
Ein Paradebeispiel für die Relevanz des Wirkungsgrades ist die klassische Glühlampe. Sie erzeugt Licht, indem Strom durch einen Draht fließt, der sich dabei so stark erhitzt, dass er zu leuchten beginnt. Dabei werden weniger als 5 % der eingesetzten Energie in Licht umgewandelt. Mehr als 95 % der Energie werden in Wärme umgewandelt. Aufgrund der schlechten Effizienz wurden Glühlampen seit 2009 in der EU schrittweise verboten. Abbildung 2 zeigt links eine klassische Glühlampe und rechts eine Energiesparlampe.

Ein hoher Wirkungsgrad ist in vielen Anwendungen erstrebenswert, da dies bedeutet, dass weniger Energie in i.d.R. nicht gewünschte Energieformen gewandelt wird, sondern dem System als Nutzenergie zur Verfügung steht. In der Praxis sind jedoch viele Faktoren wie Materialbeschaffenheit, Bauweise und Betriebsbedingungen entscheidend für die Maximierung des Wirkungsgrades. In der Umwelt- und Energietechnik spielt der Wirkungsgrad eine entscheidende Rolle, da er direkt mit dem Energieverbrauch und den Umweltauswirkungen zusammenhängt. Effizientere Systeme können dazu beitragen, den Energiebedarf zu reduzieren und Treibhausgasemissionen zu verringern.