Einleitung

Elektrische Netzwerke sind in der heutigen Welt omnipräsent. Sie bestehen aus Zusammenschaltungen von verschiedenen elektrischen Bauteilen, welche durch Verbindungsleitungen miteinander verknüpft sind. In der Realität kommen sie in den verschiedensten Funktionen und Größenordnungen vor. So kann ein elektrisches Netzwerk sowohl eine kleine elektronische Schaltung innerhalb eines Mikrocontrolers mit einer Größe von einigen Mikrometern darstellen, als auch ein elektrisches Energieverteilungsnetz mit Ausdehnungen von bis zu einigen 1000 Kilometern abbilden, wie sie symbolisch in den Abbildungen 1 bzw. 2 angedeutet sind.

Dieses Kapitel bietet eine Einführung zu grundlegenden Berechnungen in elektrischen Gleichstromnetzwerken. Ziel dieser Berechnung ist es in der Regel, die Spannungen und Ströme in allen Bauteilen des Netzwerkes zu berechnen. Reale Bauteile werden dazu in der Regel vereinfacht als Kombination idealer Zweipole dargestellt (Beispiele: Tabelle 1). Aus der Verschaltung dieser Zweipole lässt sich ein vereinfachtes Modell der realen Schaltung aufbauen, welches das grundlegende Verhalten der Schaltung nachbildet. Dieses Modell bildet die Grundlage zur mathematischen Berechnung der Schaltung.

Da in diesem Kapitel ausschließlich lineare Bauteile wie Widerstände oder ideale Gleichspannungsquellen verwendet werden, ist eine analytische Berechnung grundsätzlich immer möglich. In fortgeschrittenen Modulen werden hingegen nichtlineare Bauelemente wie reale Operationsverstärker oder Dioden eingeführt. In diesem Fall ist oft eine iterative bzw. numerische Herangehensweise notwendig.

Zweipole und Zählpfeilsysteme

1 Zweipole

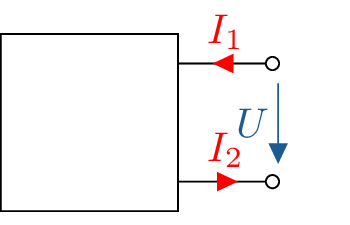
Als Zweipol (Abb. 1) wird ein Bauelement mit zwei äußeren Anschlussklemmen bezeichnet. Der innere Aufbau dieser Zweipole kann dabei von gänzlich unterschiedlicher Art und Komplexität sein. Beispielsweise ist ein einfacher elektrischer Widerstand, aber auch eine Spannungsquelle (beispielsweise eine Autobatterie) oder ein Haartrockner (sofern dieser nur zwei Anschlussleitungen besitzt) als Zweipol zu sehen. Bauteile mit mehr Anschlussleitungen werden entsprechend als Dreipol (z.B. Kühlschrank mit Schutzleiter), Vierpol (z.B. Transformator) oder gar Fünfpol (elektrischer Herd mit Drehstromanschluss, Schutzleiter und Neutralleiter) bezeichnet.

Unabhängig von der inneren Komplexität kann ein Zweipol im elektrischen Netzwerk vollständig durch die Beziehung von Strom und Spannung an seinen Anschlusspunkten, dem sogenannten Klemmenverhalten, charakterisiert werden. Zu beachten ist dabei, dass der in Abbildung 1 eingezeichnete Strom \(I_1\) eines Zweipols stets genauso groß wie der Strom \(I_2\) ist.

Die praktische Realisierung der Bauteile wie reale Baumaße, Materialeigenschaften, parasitäre Effekte oder interne inhomogene Feldstärkeverteilungen werden in der Netzwerkberechnung mit Zweipolen vernachlässigt.

Einige der bereits aus vorherigen Kapiteln bekannte Zweipole sind in Tabelle 1 beispielhaft aufgeführt.

Zweipol	Schaltzeichen
ideale Spannungsquelle
ideale Stromquelle
Kondensator (Kapazität)
ohmscher Widerstand
Spule (Induktivität)

2 Zählpfeilsysteme

Die Wahl der Zählrichtungen von Strom und Spannung ist grundsätzlich beliebig. Bei der Berechnung elektrischer Netzwerke wird häufig versucht, die Zählrichtungen so einzuführen, dass die Ströme und Spannungen positiv sind. Das ist für von vornherein bekannte Größen durchaus sinnvoll. Für unbekannte Größen muss die Zählrichtung hingegen willkürlich festgelegt werden. Es wird dadurch nicht ausgedrückt, dass der Strom tatsächlich in der Pfeilrichtung fließt bzw. eine positive Spannung in Pfeilrichtung anliegt. Die tatsächliche Richtung wird dann durch das Vorzeichen der Spannung ausgedrückt. Für eine vorzeichengerechte Beschreibung von Strömen und Spannungen ist also eine Bemaßung mit Zählpfeilen zwingend notwendig.

Bei Zweipolen wird zwischen den in Tabelle 2 vorgestellten zwei unterschiedlichen Zählpfeilsystemen unterschieden:

Zählpfeilsystem	Erzeugte Leistung	Verbrauchte Leistung	Zählpfeile am Verbraucher
VPS	P = -UI	P = UI ¿ 0
EPS	P = UI ¿ 0	P = -UI

3 Der Grundstromkreis

Die zuvor eingeführten Zweipole (oder auch Mehrpole) lassen sich zu einem elektrischen Netzwerk zusammenschließen.

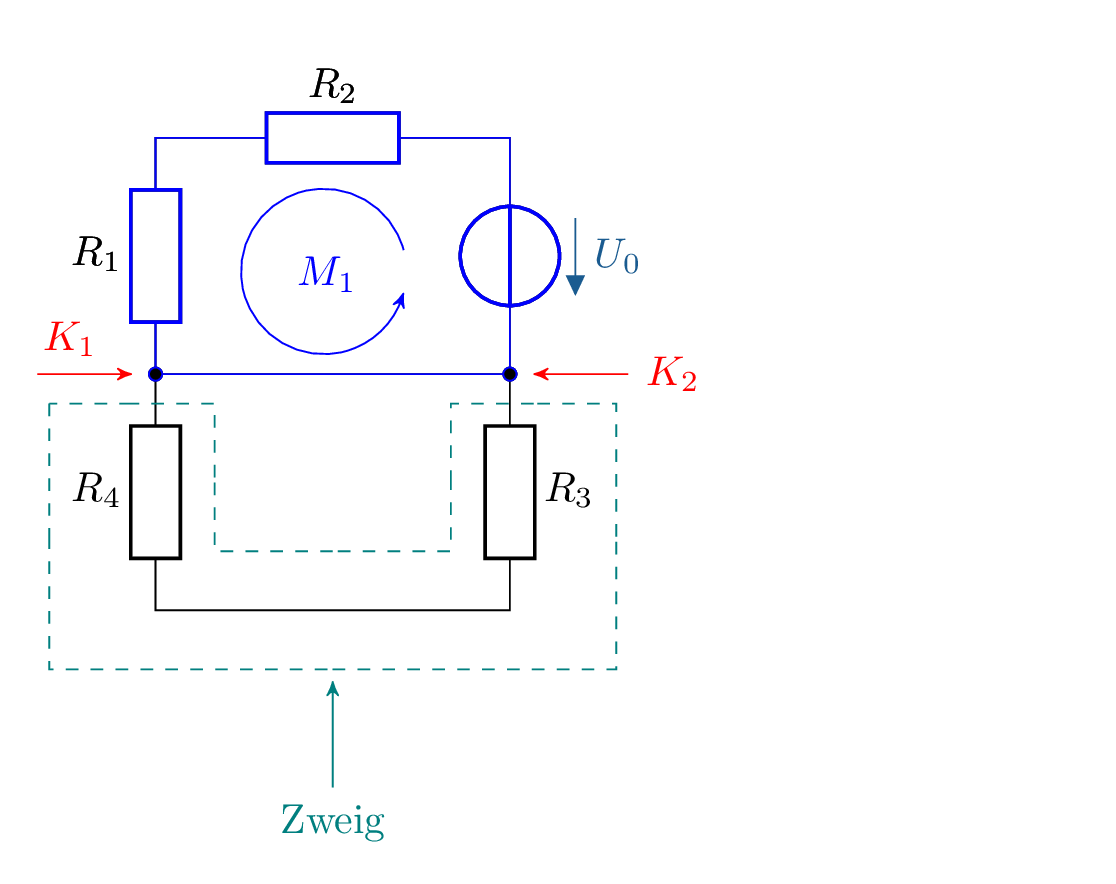
Dabei bilden die idealisierten Zweipole Zweige, die wie in Abb. 2 auch aus mehreren direkt hintereinandergeschalteten Zweipolen bestehen können. Durch alle Elemente eines Zweiges fließt der gleiche Strom. Neben dem in Abbildung 2 grün markierten Zweig bilden auch die Zweipolgruppe \(R_1\), \(R_2\) und \(U_0\) sowie der Kurzschluss in der der Zeichnung jeweils einen weiteren Zweig.

Die Verbindungspunkte, an denen sich jeweils mindestens drei Zweige treffen, werden als Knoten oder Knotenpunkte bezeichnet. Ein fließender elektrischer Strom kann sich hier auf die verschiedenen Zweige aufteilen. Das elektrische Potential ist jedoch für alle verbundenen Anschlüsse identisch. Ein Knoten wird im Schaltplan durch einen ausgefüllten Kreis gekennzeichnet und mit \(K_n\) genannt. Geschlossene Pfade von mindestens zwei sich aneinanderreihenden Zweigen innerhalb eines Netzwerkes werden Maschen genannt und mit \(M_n\) abgekürzt. Im Schaltplan wird neben der Bezeichnung der Masche häufig auch eine Umlaufrichtung mit einem Pfeil angedeutet, der die Umlaufrichtung der Masche angibt. Im hier gezeichneten Grundstromkreis lassen sich neben der eingezeichneten Masche \(M_1\) bestehend aus \(R_1\), \(R_2\), \(U_0\) und dem Kurzschluss zwischen den Knoten \(K_1\) und \(K_2\) zwei weitere Maschen finden: Der grün eingezeichnete Zweig zusammen mit dem Kurzschluss zwischen \(K_1\) und \(K_2\) bilden eine Masche \(M_2\). Eine weitere Masche \(M_3\) außen herum führt außen um die Schaltung herum und enthält alle eingezeichneten Zweipole, nicht jedoch den Kurzschluss zwischen \(K_1\) und \(K_2\).