Kirchhoffsche Sätze
Die im vorherigen Modul eingeführten Bauteilgleichungen, welche den Zusammenhang zwischen Spannung und Strom an den einzelnen Bauteilen aufzeigen, reichen nicht aus, um sämtliche Spannungen und Ströme innerhalb eines Netzwerkens zu berechnen. Die Kirchhoffschen Regeln, auch Maschen- bzw. Knotenregel genannt, liefern die hierzu benötigten Gleichungen.
Lernziele: Kirchhoffsche Regeln
Die Studierenden können
- die Kernaussagen der Kirchhoffschen Regeln wiedergeben
- die Kirchhoffschen Regeln auf einfache Widerstandsnetzwerke anwenden
1 Knotenregel (1. Kirchhoffsche Regel)
Die Knotenregel sagt aus, dass die Summe aller in einen Knoten hereinfließenden Ströme identisch zu Summe aller herausfließenden Ströme ist:
Merke:
Summe der zufließenden Ströme
=
Summe der abfließenden Ströme
Mathematisch ausgedrückt resultiert dies in folgendem Zusammenhang: \begin {equation} \sum I_\mathrm {zu} = \sum I_\mathrm {ab} \end {equation}
Dabei ist zu beachten, dass die Ströme entsprechend ihrer Zählpfeilrichtung gewertet werden. In den Knoten hereinfließende Ströme werden positiv, aus dem Knoten herausfließende Ströme werden negativ gezählt. Falls die tatsächliche Richtung eines Stromes im Vorfeld nicht bekannt ist, kann die Zählpfeilrichtung willkürlich festgelegt werden. Die tatsächliche Stromrichtung ergibt sich aus dem Zahlenwert als Rechenergebnis. Ist dieses für einen Strom negativ, sprich \(I < 0\), fließt der reale Strom in die entgegengesetzte Richtung.
Alternativ lässt sich dieser Zusammenhang auch dadurch ausdrücken, dass die Summe aller Ströme in einem Knoten gleich 0 ist:
\begin {equation} \sum _{i=1}^{n} = 0 \end {equation}
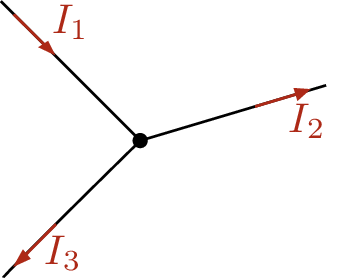
Auf den beispielhaften Knoten in Abbildung 1 angewendet ergeben sich folgende Gleichungen:
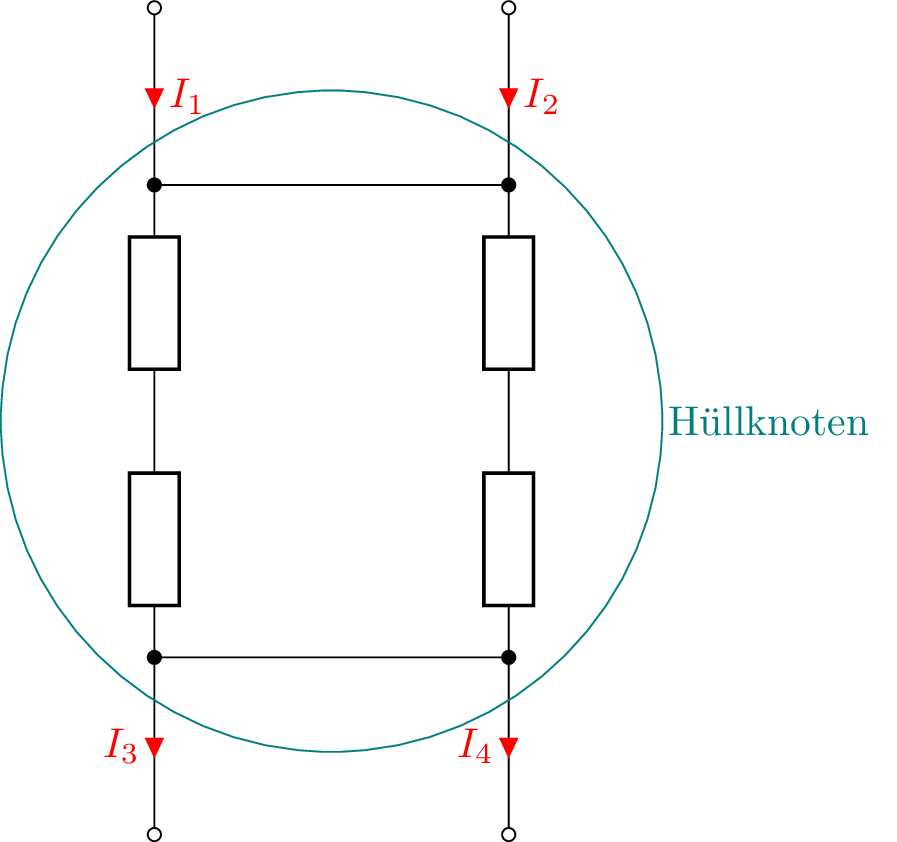
\begin {equation*} I_1 = I_2 + I_3 \end {equation*} \begin {equation*} I_1 - I_2 - I_3 = 0 \end {equation*} Der Knoten, auf den sich die Regel bezieht, muss jedoch nicht nur aus einem Punkt bestehen. Vielmehr ist möglich, sogenannte Hüllknoten zu definieren, die einen Bereich innerhalb einer Schaltung vollständig umschließen. Angewendet auf den in Abbildung 2 gezeigten Hüllknoten ergibt sich die Gleichung
\begin {equation*} I_1 + I_2 - I_3 - I_4 = 0 \end {equation*}
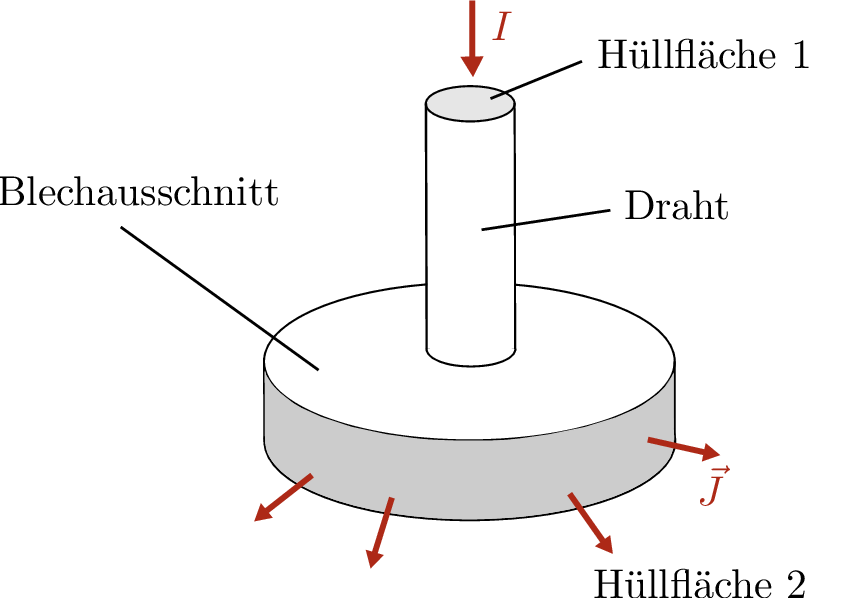
Die Knotenregel ist durch die Verallgemeinerung des Ladungserhaltungssatzes für quellenfreie Strömungsfelder nicht nur auf diskrete Bauelemente anwendbar. Vielmehr kann sie auf jede reale Struktur angewendet werden. In Abbildung 3 ist die in den Draht hereinfließende Stromstärke \(I\) folglich genauso hoch wie die gesamte Stromstärke, welche aus der Hüllfläche des Blechausschnitts heraustritt.
Allgemein lässt sich dieser Zusammenhang über das geschlossene Flächenintegral über die Hüllfläche \(\vec {A}\) beschreiben:
\begin {equation} \iint _A \vec {J} \cdot d\vec {A} = 0 \end {equation}
2 Anwendungsfall Knotenregel: Parallelschaltung von Widerständen
Ein grundlegender Anwendungsfall für die Knotenregel ist die Parallelschaltung von Widerständen. Dabei teilt sich der Strom in einem gemeinsamen Knoten und jeweils ein Teilstrom durchfließt die einzelnen Widerstände. Nach dem Passieren der jeweiligen Wiederstände vereinigen sich die Teilströme wieder, und fließen als Gesamtstrom weiter. Dargestellt ist dies in Beispiel ??.
Beispiel 1: Parallelschaltung von Widerständen
Bei der Parallelschaltung teilen sich die Ströme an den gemeinsamen Knoten auf. Wie groß
ist die Stromstärke \(I_3\) im Verhältnis zu den Stromstärken \(I_0\) bzw. \(I_1\) und \(I_2\)?
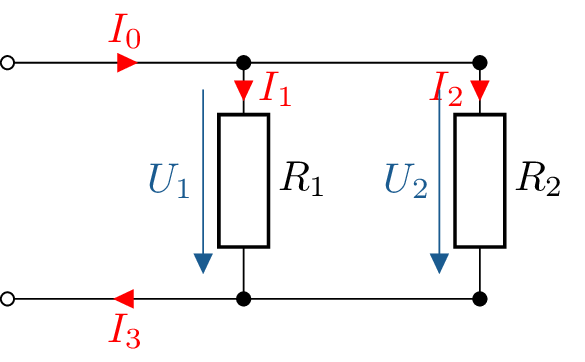
\begin {equation*} I_0-I_1-I_2 = 0 \end {equation*} \begin {equation*} \rightarrow I_0 = I_1 + I_2 \end {equation*} \begin {equation*} -I_3+I_1+I_2 = 0 \end {equation*} \begin {equation*} \rightarrow I_1+I_2 = I_3 \end {equation*} \begin {equation*} \rightarrow I_3 = I_0 \end {equation*}
Wird einer der Widerstände durch eine ideal leitende Verbindung ersetzt (Leitwert geht gegen unendlich, Widerstand folglich gegen 0), verändert sich der Stromfluss im Bereich zwischen den beiden Knoten (Beispiel ??).
Beispiel 2: Parallelschaltung mit Leiter
Ein Widerstand wird durch eine leitende Verbindung ersetzt. Wie groß sind die Stromstärken
\(I_1\) bzw. \(I_2\)?
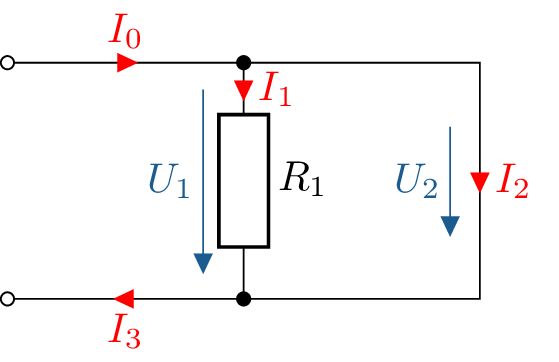
\begin {equation*} I_0=I_1+I_2 \end {equation*} \begin {equation*} \mathrm {mit} \, U_1 = R_1 \cdot I_1 \end {equation*} \begin {equation*} U_2 = R_2 \cdot I_2 =0 \stackrel {!}{=} U_1 \end {equation*} \begin {equation*} \rightarrow I_1 = 0 \end {equation*} \begin {equation*} \rightarrow I_0 = I_2 = I_3 \end {equation*}
3 Maschenregel (2. Kirchhoffscher Satz)
Der 2. Kirchhoffsche Satz (Maschenregel) besagt, dass die Summe aller Spannungen in einer Masche Null ergibt. Analog zur Richtung der Ströme muss auch hier zwingend die Richtung der einzelnen Teilspannungen berücksichtigt werden. Zeigt der Richtungspfeil einer Teilspannung entgegen der Umlaufrichtung der Masche, so muss diese Teilspannung mit einem negativen Vorzeichen versehen werden. Ist die Richtung einer anliegenden Spannung nicht bekannt, so kann auch hier eine willkürliche Zählpfeilrichtung angenommen werden. Eine gegensätzlich anliegende Spannung äußert sich in Rechnungen auch hier mit einem negativen Vorzeichen.
Gleichbedeutend mit der obigen Definition lässt sich feststellen, dass die Summe aller gleichsinnig geschalteten Spannungen an Spannungsquellen der Spannung entspricht, welche an den Verbrauchern abfällt.
Merke: Maschenregel 2
Spannungssumme an Spannungsquellen = Spannungssumme an Verbrauchern
Angewendet auf das in Abbildung 4 gezeigte Beispielnetzwerk ergeben sich folgende Maschengleichungen:
\begin {equation*} U_1+U_2-U_3-U_4 =0 \end {equation*} beziehungsweise
\begin {equation*} U_1+U_2 = U_3+U_4 \end {equation*}
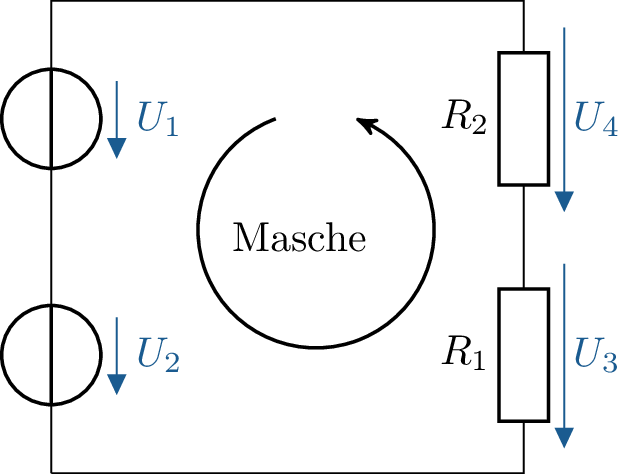
Die Maschengleichung gilt auch, falls in die Masche zusätzliche Ströme eingespeist werden, oder einzelne Zweipole während des Umlaufs um eine geschlossene Masche mehrfach durchlaufen werden.
Der allgemeine Zusammenhang, jegliche aufintegrierte Spannung entlang einer geschlossene Kontur 0 ergibt, kann nach den Maxwell Gleichungen folgendermaßen beschrieben werden:
\begin {equation} \oint _{s} \vec {E} d\vec {s} = 0 \end {equation}
4 Anwendungsfall Maschenregel: Reihenschaltung von Widerständen
Während die Knotenpunkte in elektrischen Netzwerken vor allem für den Strom von Bedeutung sind, sind die Zweige und somit auch Maschen vor allem für die Berechnung der Spannungen von Interesse. Bei einer Reihenschaltung von Widerständen in einem Zweig addieren sich alle Teilspannungen vorzeichenrichtig zu einer Gesamtspannung auf. Ein Anwendungsfall zur Ermittlung einer Teilspannung ist in Beispiel ?? dargestellt.
Beispiel 3: Reihenschaltungen in Netzwerken
Bei der Reihenschaltung addieren sich die Spannungen zu einer Gesamtspannung auf.
Wie groß ist die Spannung \(U_0\)?
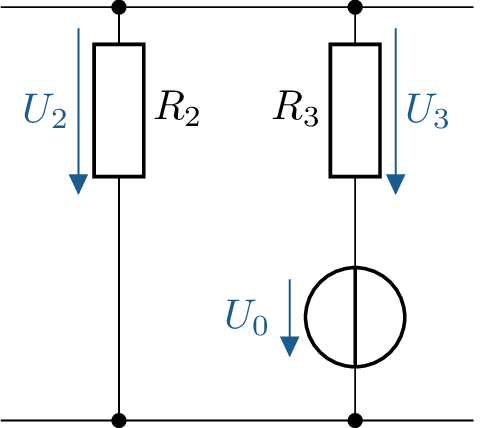
Masche entgegen dem Uhrzeigersinn aufstellen:
\begin {equation*} U_2-U_0-U_3 =0 \end {equation*}
\begin {equation*} \rightarrow U_0 = U_2- U_3 \end {equation*}
Die Maschenregel lässt sich auch anwenden, wenn die Masche, auf die sie angewendet wird, eine Unterbrechungsstelle hat (siehe Beispiel ??).
Beispiel 4: Reihenschaltungen mit Unterbrechungsstelle
Eine Verbindung wird unterbrochen. Wie groß ist die Spannung \(U_1\) an der Unterbrechungsstelle?
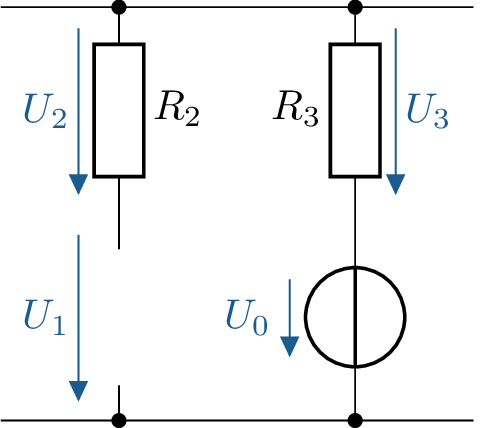
Masche entgegen dem Uhrzeigersinn aufstellen:
\begin {equation*} U_2+U_1-U_0-U_3 = 0 \end {equation*}
Ermitteln der Spannung \(U_2\) mit Hilfes des Ohmschen Gesetzes:
\begin {equation*} U_2=I_2 \cdot R_2 \end {equation*}
\begin {equation*} \rightarrow I_2 = 0 \end {equation*}
\begin {equation*} \rightarrow U_2 = 0 \end {equation*}
Einsetzen in Ausgangsgleichung und nach \(U_1\) auflösen:
\begin {equation*} U_1 = U_0 + U_3 \end {equation*}