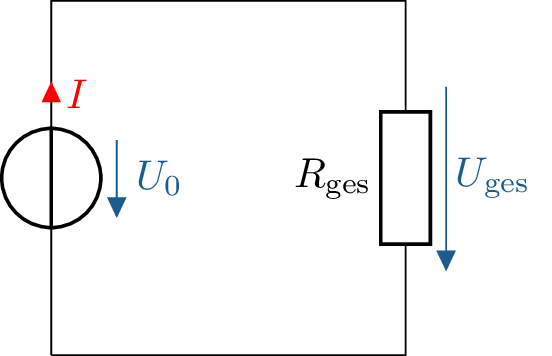GET it digital

Einfache Widerstandsnetzwerke

Elektrische Netzwerke setzen sich häufig aus einfacheren Teilschaltungen zusammen. Oft ist es hilfreich, diese Teilschaltungen zu identifizieren, zu vereinfachen und anschließend zur Gesamtschaltung zusammenzufassen. Solche Zusammenfassungen von Bauelementen sind grundsätzlich zulässig, sofern sich das Klemmverhalten, also das Verhalten zwischen Strom und Spannung zwischen den Anschlusspunkten, nicht ändert.

Lernziele: Einfache Widerstandsnetzwerke

Die Studierenden können

Teilschaltungen in gleichstromnetzwerken identifizieren
Widerstandsnetzwerke vereinfachen und zusammenfassen
Kurzschluss- sowie Leerlaufdaten bestimmen
Überlagerungsverfahren anwenden

1 Reihenschaltung von Widerständen

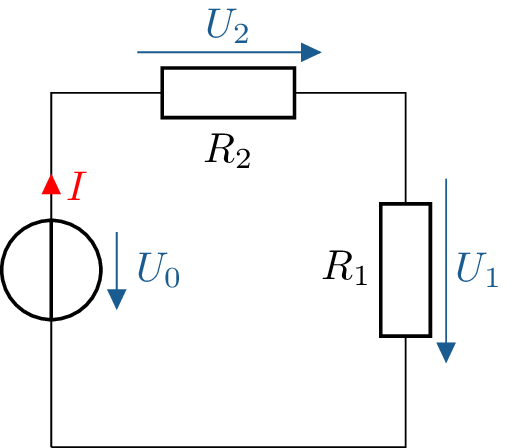
In einer Reihenschaltung werden alle Bauelemente vom gleichen Strom \(I\) durchflossen (siehe Abbildung 1).

Schematische Darstellung einer Reihenschaltung bestehend aus einer Spannungsquelle U0 und zwei
in Serie geschalteten Widerständen R1 und R2. Der elektrische Strom I verläuft im Uhrzeigersinn
durch die Schaltung. — Abbildung 1: Reihenschaltung von zwei Widerständen und einer Spannungsquelle

Das Anwenden der Maschenregel (hier: Umlaufrichtung gegen den Uhrzeigersinn) führt zu folgender Maschengleichnung:

\begin {equation*} U_0 - U_1 - U_2 =0 \end {equation*}

Mit Hilfe des Ohmschen Gesetzes können die Teilspannungen \(U_1\) und \(U_2\) als Produkt aus Stromstärke und Widerstand dargestellt werden:

\begin {equation*} U_0 - R_1 \cdot I - R_2 \cdot I = 0 \end {equation*} \begin {equation*} U_0 - (R_1+R_2) \cdot I = 0 \end {equation*}

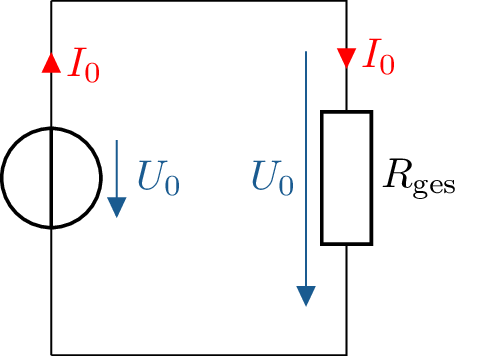
Die Widerstände \(R_1\) und \(R_2\) lassen sich in diesem Beispiel durch Addition ihrer Widerstandswerte zu \(R_1 + R_2 = R_\mathrm {ges}\) zusammenfassen (Abbildung 2).

Darstellung einer elektrischen Schaltung. Eine Spannungsquelle U0 treibt den Strom I im
Uhrzeigersinn durch die Schaltung. Der Gesamtwiderstand Rges ist rechts im Stromkreis
eingezeichnet, über ihm liegt die Spannung Uges, die mit einem Pfeil nach unten gekennzeichnet ist.
Die Spannung U0 der Quelle ist ebenfalls nach unten gerichtet. — Abbildung 2: Zusammenfassen von \(R_1\) und \(R_2\) zu \(R_\mathrm {ges}\)

Allgemein lässt sich die Gesamtspannung \(U_\mathrm {ges}\) nach diesem Prinzip folgendermaßen zusammenfassen:

\begin {equation} U_\mathrm {ges} = \sum _{k=1}^{n} U_k = \sum _{k=1}^{n} R_k \cdot I = R_\mathrm {ges} \cdot I \label {eq:gesamtwiderstand} \end {equation}

Ein Koeffizientenvergleich der letzten beiden Terme von Gleichung 1 liefert das allgemeingültige Ergebnis, um Widerstände in einer Reihenschaltung zusammenzufassen:

Merke: Gesamtwiderstand einer Reihenschaltung

\begin {equation} R_\mathrm {ges} = \sum _{k=1}^{n} R_k \end {equation}

Betrachtet man statt der Widerstandswerte \(R\) die Leitwerte \(G = 1/R\) der Widerstände, ergibt sich für den Gesamtleitwert einer Reihenschaltung:

Merke: Gesamtleitwert einer Reihenschaltung

\begin {equation} \frac {1}{G_\mathrm {ges}} = \sum _{k=1}^{n} \frac {1}{G_k} \end {equation}

2 Parallelschaltung von Widerständen

In einer Parallelschaltung von Widerständen liegt an allen Bauelementen die selbe Spannung an (siehe Abbildung 3):

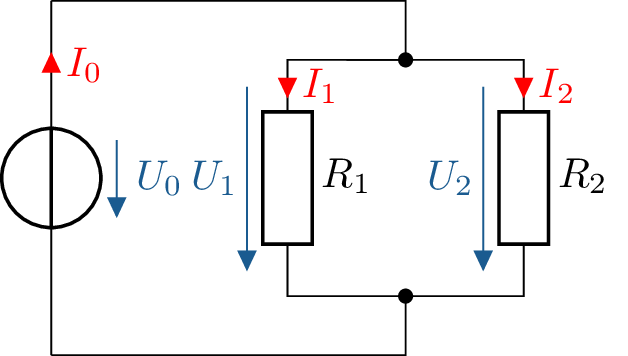
Schaltskizze einer elektrischen Parallelschaltung mit zwei Widerständen R1 und R2, die an eine
Spannungsquelle U0 angeschlossen sind. Der Gesamtstrom I0 teilt sich am oberen Knoten in die
Teilströme I1 durch R1 und I2 durch R2 auf. Beide Widerstände sind parallel zwischen denselben
Knoten verbunden und werden von den Spannungen U1 beziehungsweise U2 durchflossen, die
identisch zur Quellenspannung U0 ausgerichtet sind. Alle Spannungen sind durch Pfeile nach unten
dargestellt. — Abbildung 3: Parallelschaltung von zwei Widerständen und einer Spannungsquelle

\begin {equation*} U_\mathrm {1} = U_\mathrm {2} = U_0 \end {equation*}

Durch das Anwenden der Knotenregel lässt sich zeigen, dass sich der Gesamtstrom \(I_0\) vor den Widerständen in die Teilströme \(I_1\) und \(I_2\) aufteilt:

\begin {equation} I_0 - I_1 - I_2 = 0 \label {eq:gesamtwiderstand2} \end {equation}

Wie bei der Reihenschaltung im Kapitel 4.1 ist es auch bei der Parallelschaltung von Widerständen häufig von Vorteil, diese zu einem Gesamtwiderstand \(R_\mathrm {ges}\) zusammenzufassen (siehe Abbildung 4):

Mit Hilfe des Ohmschen Gesetzes können die unbekannten Teilströme \(I_1\) und \(I_2\) aus der Knotenregel (Gleichung 4) quantifiziert werden:

\begin {equation*} I_1 = \frac {U_0}{R_1}, I_2 = \frac {U_0}{R_2} \end {equation*}

Eingesetzt in Gleichung 4 ergibt sich:

\begin {equation*} I_0 - \frac {U_0}{R_1} - \frac {U_0}{R_2} = 0 \end {equation*}

\begin {equation*} I_0 - \bigg ( \frac {1}{R_1}+\frac {1}{R_2} \bigg ) \cdot U_0 = 0 \end {equation*}

\begin {equation*} \rightarrow I_0 = U_0 \cdot \bigg ( \frac {1}{R_1}+\frac {1}{R_2} \bigg ) \end {equation*}

Ein Koeffizientenvergleich mit dem auf Abbildung 4 angewandten Ohmschen Gesetz ( \(I_0 = U_0 \cdot \frac {1}{R_\mathrm {ges}}\))

liefert für \(R_\mathrm {ges}\) im gezeigten Fall von zwei parallel geschalteten WIderständen:

\begin {equation*} \frac {1}{R_\mathrm {ges}} = \frac {1}{R_1}+\frac {1}{R_2} \end {equation*}

Das Ausmultiplizieren dieses Ausdrucks ergibt die in Rechnungen häufig genutzte Form:

\begin {equation} R_\mathrm {ges} = \frac {R_1\cdot R_2}{R_1 + R_2} \label {eq:r2parallel} \end {equation}

Der Gesamtwiderstand einer Parallelschaltung aus beliebig vielen Widerständen lässt sich mit Hilfe der allgemeinen Formel für Parallelschaltungen ermitteln:

Merke: Gesamtwiederstand einer Parallelschaltung

\begin {equation} \frac {1}{R_\mathrm {ges}} = \sum _{k=1}^{n} \frac {1}{R_k} \label {eq:rparallel} \end {equation}

Da der elektrische Leitwert durch den Kehrwert des Widerstandes \(G=1/R\) beschrieben wird, ist der Gesamtleitwert einer Parallelschaltung von Widerständen oft leichter zu berechnen:

Merke: Gesamtleitwert einer Parallelschaltung

\begin {equation} G_\mathrm {ges} = \sum _{k=1}^{n} G_k \end {equation}

Beispiel 1: Parallelschaltung von Widerständen

Die drei Widerstände \(R_1 = 1 \, \mathrm {k}\Omega \), \(R_2 = 10 \, \mathrm {k}\Omega \), \(R_3 = 100 \, \mathrm {k}\Omega \) werden wie in folgender Abbildung gezeigt parallel geschaltet. Wie groß ist der Gesamtwiderstand \(R_\mathrm {ges}\) dieser Parallelschaltung?

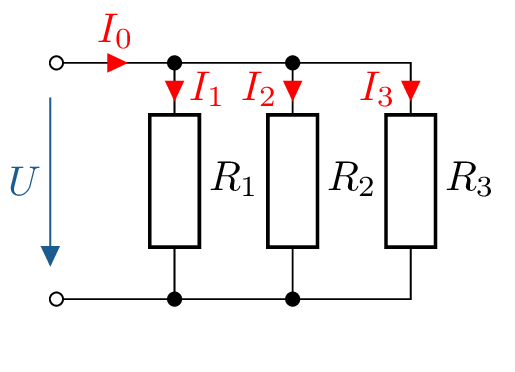
Darstellung einer Parallelschaltung mit drei Widerständen R1, R2 und R3, die an eine
gemeinsame Spannung U angeschlossen sind. Der Gesamtstrom I0 teilt sich am oberen
Knoten in die Teilströme I1, I2 und I3 auf.

Aufstellen der Gleichung für \(R_\mathrm {ges}\) nach Gleichung 6:

\begin {equation*} R_\mathrm {ges} = \frac {1}{\sum _{n} \frac {1}{R_n}} = \frac {1}{\frac {1}{R_1} + \frac {1}{R_2}+ \frac {1}{R_3}} \end {equation*}

Einsetzen der Zahlenwerte und Lösung mittels Taschenrechner:

\begin {equation*} R_\mathrm {ges} = \frac {1}{\frac {1}{1\cdot 10^3 \, \Omega } + \frac {1}{10\cdot 10^3 \, \Omega } + \frac {1}{100 \cdot 10^3 \, \Omega }} \end {equation*}

\begin {equation*} \rightarrow R_\mathrm {ges} = 900,9 \, \Omega \end {equation*}

3 Spannungsteiler an Widerständen

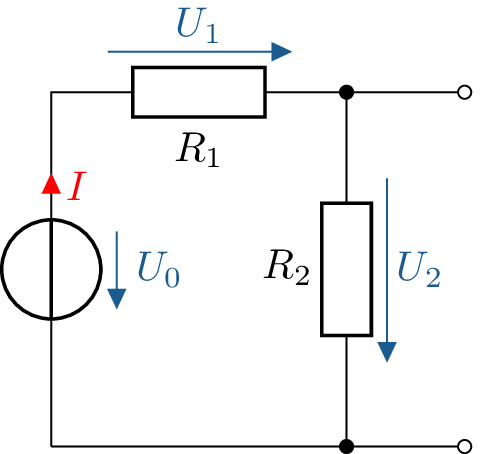
Ein Anwendungsfall der Reihenschaltung von zwei Widerständen ist der Spannungsteiler. Er wird genutzt, um eine Eingangsspannung \(U_0\) in zwei kleinere Teilspannungen aufzuteilen, und so eine genau definierte Ausgangsspannung \(U_2\) bereitzustellen.

3.1 Der unbelastete Spannungsteiler

Zunächst sei der in Abbildung 5 dargestellte Spannungsteiler unbelastet, d.h. es ist kein Lastwiderstand an den offenen Klemmen angeschlossen. Alle Bauelemente werden vom gleichen Strom \(I\) durchflossen:

Schematische Darstellung eines unbelasteten Spannungsteilers mit zwei Widerständen R1 und R2.
Die Spannungsquelle mit der Spannung U0 treibt den Strom I durch den oberen Widerstand R1, an
dem die Teilspannung U1 abfällt. Der zweite Widerstand R2 ist in Reihe geschaltet, über ihm liegt
die Spannung U2. Beide Spannungen U1 und U2 addieren sich zur Gesamtspannung U0. Der
Strompfeil I ist rot eingezeichnet, die Spannungspfeile U0, U1 und U2 sind blau dargestellt. — Abbildung 5: Unbelasteter Spannungsteiler

\begin {equation*} I = \frac {U_1}{R_1} = \frac {U_2}{R_2} \end {equation*}

Durch Zusammenfassen der Reihenschaltung aus Widerständen ergibt sich:

\begin {equation*} I = \frac {U_0}{R_1+R_2} \end {equation*}

Durch Gleichsetzen der beiden Spannungsterme ergibt sich die Verhältnisgleichung:

\begin {equation*} \frac {U_2}{R_2} = \frac {U_0}{R_1+R_2} \end {equation*}

Isolieren der Ausgangsspannung auf der linken Seite des Gleichheitsszeichens führt letztendlich zur allgemeine Gleichung für den unbelasteten Spannungsteiler:

Merke: Unbelasteter Spannungsteiler

\begin {equation} U_2 = U_0 \cdot \frac {R_2}{R_1+R_2} \end {equation}

Beispiel 2: Unbelasteter Spannungsteiler

Eine Eingangsspannung von \(U_0 = 24\) V soll mit einem Spannungsteiler auf \(U_2 = 6\) V reduziert werden. Wie ist das Verhältnis der Widerstände von \(R_2\) zu \(R_1\) zu wählen? Wie groß sind die Widerstände \(R_1\) und \(R_2\) zu wählen, wenn der Gesamtstrom \(I = 10\) mA betragen soll?

\begin {equation*} \frac {U_2}{U_0} = \frac {6 \, \mathrm {V}}{24 \, \mathrm {V}} = 0,25 = \frac {R_2}{R_1+R_2} \end {equation*}

\begin {equation*} \rightarrow R_2 = 0.25 (R_1+R_2) \end {equation*}

\begin {equation*} 0.75 \, R_2 = 0.25 \, R_1 \end {equation*}

\begin {equation*} R_1 = 3 \, R_2 \end {equation*}

Der Widerstand \(R_1\) muss also drei mal so groß wie der Widerstand \(R_2\) gewählt werden.

\begin {equation*} I = \frac {U_2}{R_2} \rightarrow R_2 = \frac {U_2}{I} = \frac {5 \, \mathrm {V}}{0.01 \mathrm {A}} = 500 \, \Omega \end {equation*}

\begin {equation*} R_1 = 3 \cdot R_2 = 3 \cdot 500 \, \Omega = 1500 \, \Omega \end {equation*}

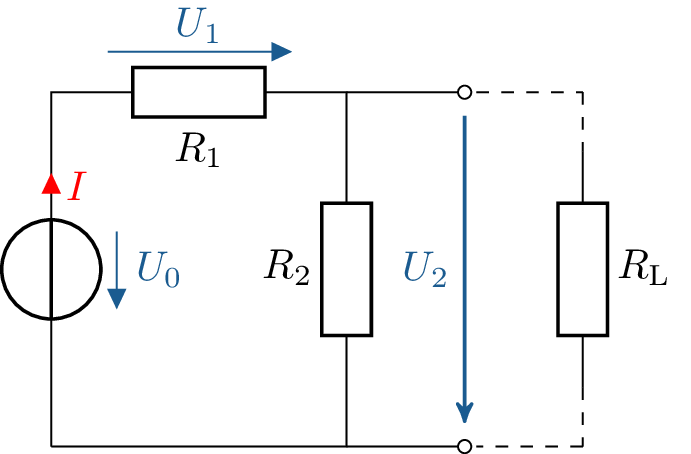
3.2 Der belastete Spannungsteiler

Wird die Ausgangsseite des Spannungsteilers wie in Abbildung 6 belastet, also beispielsweise ein Lastwiderstand \(R_\mathrm {L}\) hinzugefügt, so ergibt sich - von der Spannungsquelle aus gesehen - eine Parallelschaltung der Widerstände \(R_2\) und \(R_\mathrm {L}\).

Wird der Ersatzwiderstand \(R_\mathrm {neu}\) dieser Parallelschaltung über \(\frac {1}{R_\mathrm {neu}} = \frac {1}{R_2} + \frac {1}{R_\mathrm {L}}\) ermittelt, ändert sich das Verhältnis der Widerstände des Spannungsteilers, und folglich auch die Ausgangsspannung. Diese Änderung muss bei der Auslegung eines belasteten Spannungsteilers mit beachtet werden.

Schematische Darstellung eines belasteten Spannungsteilers mit einer Spannungsquelle U0, den
Widerständen R1 und R2 sowie einem zusätzlichen Lastwiderstand RL. Die Spannungsquelle U0
treibt den Strom I durch R1, an dem die Spannung U1 abfällt. Die Spannung U2 liegt über dem
Parallelzweig aus R2 und RL, der durch eine gestrichelte Linie hervorgehoben ist. Der Strompfeil I
ist rot markiert, die Spannungspfeile U0, U1 und U2 sind in Blau dargestellt. — Abbildung 6: Mit dem Widerstand \(R_\mathrm {L}\) belasteter Spannungsteiler

Beispiel 3: Belasteter Spannungsteiler

Ein Spannungsteiler soll eine Eingangsspannung von \(U_0 = 20\) V auf die Ausgangsspannung von \(U_2 = 5\) V reduzieren. Der Spannungsteiler wird mit \(R_\mathrm {L} = 200 \, \Omega \) belastet. Vorgegeben ist der Widerstand \(R_1 = 300 \, \Omega \).

Wie groß muss \(R_2\) dimensioniert werden, um die gewünschte Ausgangsspannung zu erreichen?

Zunächst muss der benötigte Gesamtwert \(R_\mathrm {neu}\) der Parallelschaltung aus \(R_\mathrm {L}\) und \(R_2\) berechnet werden:

\begin {equation*} U_2 = U_0 \cdot \frac {R_\mathrm {neu}}{R_1+R_\mathrm {neu}} \end {equation*}

\begin {equation*} R_\mathrm {neu} = \frac {5 \, \mathrm {V}}{20 \, \mathrm {V}} \cdot (R_1 + R_\mathrm {neu}) \end {equation*}

\begin {equation*} 0.75 \cdot R_\mathrm {neu} = 0.25 \cdot R_1 = 75 \, \Omega \end {equation*}

\begin {equation*} \rightarrow R_\mathrm {neu} = 100 \, \Omega \end {equation*}

Der Widerstand \(R_1\) ist mit Hilfe der Formel für Parallelschaltungen zu berechnen:

\begin {equation*} 100 \, \Omega = \frac {R_\mathrm {L} \cdot R_2}{R_\mathrm {L} + R_2} = \frac {200 \, \Omega \cdot R_2}{200 \, \Omega + R_2} \end {equation*}

\begin {equation} R_2 \cdot \frac {200 \, \Omega }{100 \, \Omega } = 2 \cdot R_2 = 200 \, \Omega + R_2 \end {equation}

\begin {equation*} \rightarrow R_2 = 200 \, \Omega \end {equation*}

4 Stromteiler in Widerstandsnetzwerken

Eine wie in Abbildung 7 dargestellte Parallelschaltung von zwei Widerständen teilt einen in eine Schaltung fließenden Strom \(I_0\) in zwei Teilströme \(I_1\) sowie \(I_2\). Eine solche Schaltung wird als Stromteiler bezeichnet.

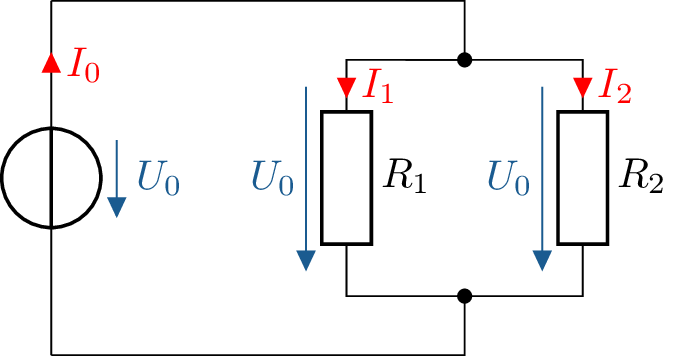
Schaltskizze einer Parallelschaltung mit zwei Widerständen R1 und R2, die an einer gemeinsamen
Spannungsquelle U0 betrieben werden. Der Gesamtstrom I0 teilt sich in die Teilströme I1 und I2
auf, die durch R1 bzw. R2 fließen. Alle Spannungen über den Widerständen sind mit U0 bezeichnet
und verlaufen vertikal nach unten, während die Strompfeile I0, I1 und I2 rot markiert sind. — Abbildung 7: Stromteiler der Stromstärke \(I_0\) in die Teilstromstärken \(I_1\) und \(I_2\), bestehend aus den parallel geschalteten Widerständen \(R_1\) und \(R_2\)

An allen Bauelementen dieser Schaltung liegt die identische Ausgangsspannung \(U_0\) an. Mit Hilfe des Ohmschen Gesetzes lässt sich diese Spannung über den Widerständen \(R_1\) und \(R_2\) auch als Produkt von Widerstandswert und der Stromstärke umschreiben:

\begin {equation*} U_0 = I_1 \cdot R_1 = I_2 \cdot R_2 \end {equation*}

Durch das wie in Abbildung 4 beschriebene Zusammenfassen der Widerstände \(R_1\) und \(R_2\) zu \(R_\mathrm {ges}\) lässt sich der Gesamtstrom \(I_0\) in Abhängigkeit der Ausgangsspannung \(U_0\) ermitteln:

\begin {equation*} U_0 = I_0 \cdot R_\mathrm {ges} \end {equation*}

Durch Gleichsetzen der beiden Stromterme ergibt sich folgendes Verhältnis zwischen \(I_0\) und \(I_2\)

\begin {equation*} I_2 \cdot R_2 = I_0 \cdot R_\mathrm {ges} \end {equation*}

Die Parallelschaltung \(R_\mathrm {ges}\) lässt sich wie in Gleichung 5 gezeigt direkt aus den beiden Widerstandswerten \(R_1\) und \(R_2\) errechnen:

\begin {equation*} I_2 \cdot R_2 = I_0 \cdot \frac {R_1 \cdot R_2}{R_1 + R_2} \end {equation*}

Das Kürzen von \(R_2\) resultiert im Teilungsverhältnis der elektrischen Stromstärke am Stromteiler:

Merke: Stromteiler einer Parallelschaltung

\begin {equation} I_2 = I_0 \cdot \frac {R_1}{R1 + R_2} \end {equation}

5 Besondere Betriebszustände aktiver Zweipole

Aktive Zweipole lassen sich zu Ersatzspannungsquellen beziehungsweise Ersatzstromquellen zusammenfassen. Dies kann vor allem zur Vereinfachung von elektrischen Netzwerken dienlich sein.

5.1 Kurzschluss- und Leerlaufversuch an der Ersatzspannungsquelle

Die reale Spannungsquelle

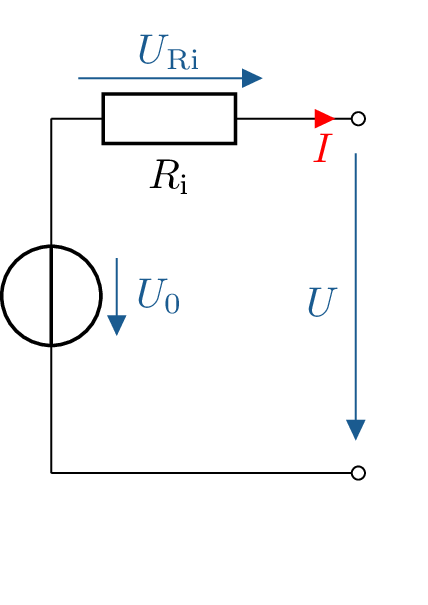
Eine reale Spannungsquelle besteht wie bereits aus Modul 3 Elektrische Bauelemente bekannt aus einer idealen Spannungsquelle \(U_0\) sowie einem Innenwiderstand \(R_\mathrm {i}\).

Schaltskizze einer realen Spannungsquelle,
bestehend aus einer idealen Spannungsquelle
U0 und einem in Reihe geschalteten
Innenwiderstand Ri. Über dem
Innenwiderstand liegt die Spannung URi an,
und der Strom I fließt nach rechts zum
Ausgang der Quelle. Die Klemmenspannung
U wird zwischen dem Ausgangspunkt und
dem unteren Anschluss gemessen. — Abbildung 8: Aus einer idealen Spannungsquelle \(U_0\) und einem Innenwiderstand \(R_\mathrm {i}\) bestehende reale Spannungsquelle

Schaltskizze einer realen Spannungsquelle
mit angeschlossenem Lastwiderstand Ra. Die
ideale Spannungsquelle U0 ist in Reihe mit
dem Innenwiderstand Ri geschaltet. Über Ri
fällt die Spannung URi = R·I ab, während
der Strom I durch den Lastwiderstand Ra
fließt. Die Klemmenspannung U wird
parallel zu Ra gemessen. — Abbildung 8: Aus einer idealen Spannungsquelle \(U_0\) und einem Innenwiderstand \(R_\mathrm {i}\) bestehende reale Spannungsquelle

Ist die reale Spannungsquelle unbelastet, also kein Bauteil an den Ausgangsklemmen angeschlossen, fließt kein Strom \(I\)(siehe Abbildung 8).

\begin {equation*} I = 0 \end {equation*}

\begin {equation*} \rightarrow U_\mathrm {Ri} = R_\mathrm {i} \cdot I = 0 \end {equation*}

Da die Spannung über dem Innenwiderstand \(R_\mathrm {i}\) 0 Volt beträgt, gilt für die Klemmspannung \(U\):

\begin {equation*} U = U_0 \end {equation*}

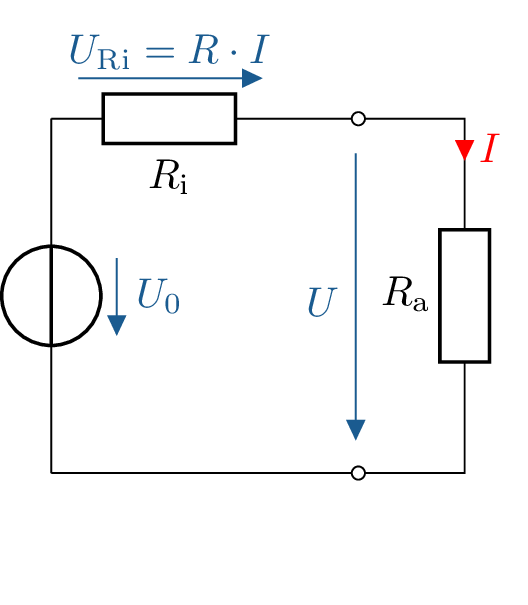
Wird die reale Spannungsquelle wie in Abbildung 9 gezeigt mit einem Widerstand \(R_\mathrm {a}\) belastet, fließt ein Strom \(I > 0\) durch die Leitung.

Folglich fällt an dem Innenwiderstand \(R_\mathrm {i}\) eine Spannung \(U_\mathrm {Ri} = R_\mathrm {i} \cdot I\) ab, und die Klemmspannung beträgt

\begin {equation*} U = U_0 - U_\mathrm {Ri} \end {equation*}

Um den Spannungsabfall innerhalb der Spannungsquelle zu reduzieren, sollte der Innenwiderstand \(R_\mathrm {i}\) möglichst klein gehalten werden:

\begin {equation*} U_0 << I \cdot R_\mathrm {i} \end {equation*}

Die Ersatzspannungsquelle

Jeder aktive Zweipol mit mindestens einer Quelle und beliebig vielen Widerständen kann zu einer Ersatzspannungsquelle (Abbildung 10) zusammengefasst werden. Wie bei einer realen Spannungsquelle genügt die Bestimmung einer idealen Spannungsquelle \(U_0\) sowie eines zusammengefassten Innenwiderstandes \(R_\mathrm {i}\), um die Ersatzspannungsquelle vollständig zu charakterisieren. Sie verfügt nach außen hin über ein vollständig gleichwertiges Klemmverhalten wie die originale Schaltung an ihren zwei Anschlussklemmen.

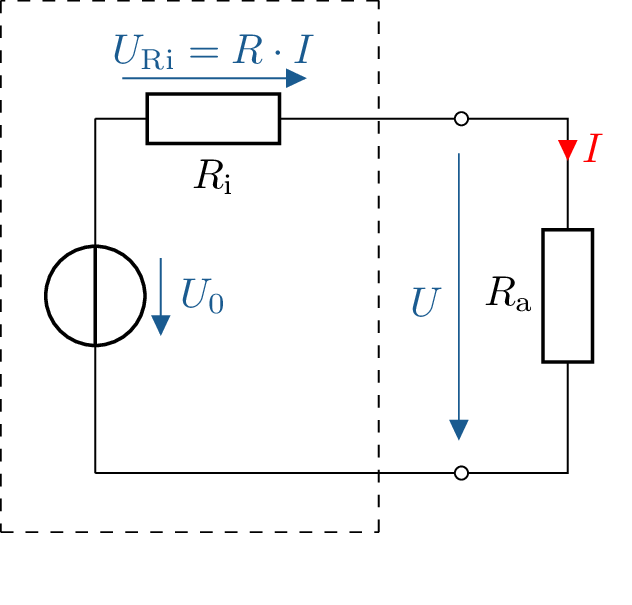
Schaltskizze einer Ersatzspannungsquelle, deren Aufbau einer realen Spannungsquelle entspricht.
Die ideale Spannungsquelle U0 und der Innenwiderstand Ri befinden sich innerhalb eines
gestrichelten Kastens, der die Ersatzspannungsquelle kennzeichnet. Über Ri fällt die Spannung URi
= R·I ab. Der Strom I fließt durch den angeschlossenen Lastwiderstand Ra, über dem die
Klemmenspannung U anliegt. — Abbildung 10: Die Ersatzspannungsquelle (gestrichelter Kasten) verfügt über das gleiche Ersatzschaltbild wie eine reale Spannungsquelle

Wie bei einer belasteten realen Spannungsquelle ist die resultierende Ausgangsspannung \(U\) sowohl vom Innenwiderstand \(R_\mathrm {i}\) als auch vom Belastungsstrom \(I\) abhängig (Abbildung 11):

\begin {equation*} U = U_0 - I \cdot R_\mathrm {i} \end {equation*}

Abbildung 11: Die an den Klemmen der Ersatzspannungsquelle anliegende Spannung \(U\) in Abhängigkeit von der resultierenden Stromstärke \(I\)

Die zur Charakterisierung notwendigen Parameter \(U_0\) und \(R_\mathrm {i}\) können mit Hilfe von zwei Versuchen ermittelt werden: dem Kurzschlussversuch sowie dem Leerlaufversuch.

Beim Leerlaufversuch werden die beiden Klemmen der Ersatzspannungsquelle offen gelassen (Abbildung 12).

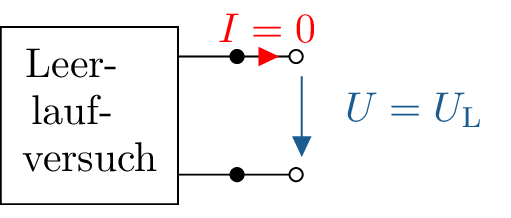
Schematische Darstellung zur Bestimmung der Leerlaufspannung UL einer Ersatzspannungsquelle.
Der Spannungsquelle ist als Zweipol dargestellt, dessen Ausgang offen ist, sodass kein Strom fließt.
Zwischen den offenen Klemmen liegt die gemessene Spannung U = UL an, die der
Leerlaufspannung der Quelle entspricht. — Abbildung 12: Ermittlung der Leerlaufspannung \(U_\mathrm {L}\) einer Ersatzspannungsquelle

Da durch die offenen Klemmen der Strom \(I\) durch den Widerstand \(R_\mathrm {i}\) null Ampere beträgt, fällt auch keine Spannung über ihn ab. Die Leerlaufspannung ist also mit der Spannung \(U_0\) identisch:

Merke: Leerlaufspannung einer Ersatzspannungsquelle

\begin {equation*} U_0 = U_\mathrm {L} \end {equation*}

Beim Kurzschlussversuch werden die beiden Klemmen des aktiven Zweipols direkt kurzgeschlossen, sprich eine ideal leitende Verbindung zwischen ihnen hergestellt (Abbildung 13).

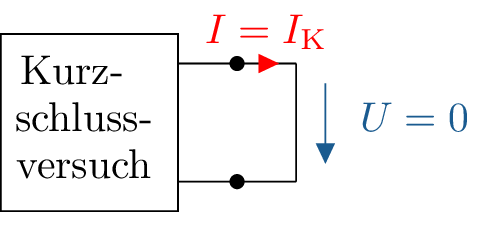
Schematische Darstellung zur Bestimmung des Kurzschlusstroems IK einer Ersatzspannungsquelle.
Der Spannungsquelle ist als Zweipol dargestellt, dessen Ausgang kurzgeschlossen ist, sodass keine
Spannung abfällt. Zwischen den Klemmen fließt der Strim IK — Abbildung 13: Ermittlung des Kurzschlussstromes \(I_\mathrm {K}\) einer Ersatzspannungsquelle

Über dem so erzeugten Kurzschluss kann keine Ausgangsspannung \(U\) anliegen:

\begin {equation*} U = 0 \end {equation*}

Folglich fällt die gesamte von \(U_0\) generierte Spannung am Innenwiderstand \(R_\mathrm {i}\) ab. Dem Ohmschen Gesetz folgend bestimmt dieser damit den Kurzschlussstrom \(I_\mathrm {K}\).

\begin {equation*} U_\mathrm {Ri} = U_\mathrm {L} =R_\mathrm {Ri} \cdot I_\mathrm {K} \end {equation*}

Der Kurzschlussstrom \(I_\mathrm {K}\) beträgt folglich:

\begin {equation*} I_\mathrm {K} = \frac {U_\mathrm {L}}{R_\mathrm {i}} \end {equation*}

Somit kann der Innenwiderstand \(R_\mathrm {i}\) folgendermaßen berechnet werden:

Merke: Innenwiderstand einer Ersatzspannungsquelle

\begin {equation*} R_\mathrm {i} = \frac {U_\mathrm {L}}{I_\mathrm {K}} \end {equation*}

Achtung: \(U_\mathrm {L}\) und \(I_\mathrm {K}\) sind in zwei vollkommen unabhängigen Versuchen bestimmte Größen, die nicht gleichzeitig auftreten. Die Formel sieht also nur wie Ohmsches Gesetz am Widerstand \(R_\mathrm {i}\) aus, ist es aber nicht.

5.2 Kurzschluss- und Leerlaufversuch an der Ersatzstromquelle

Die reale Stromquelle

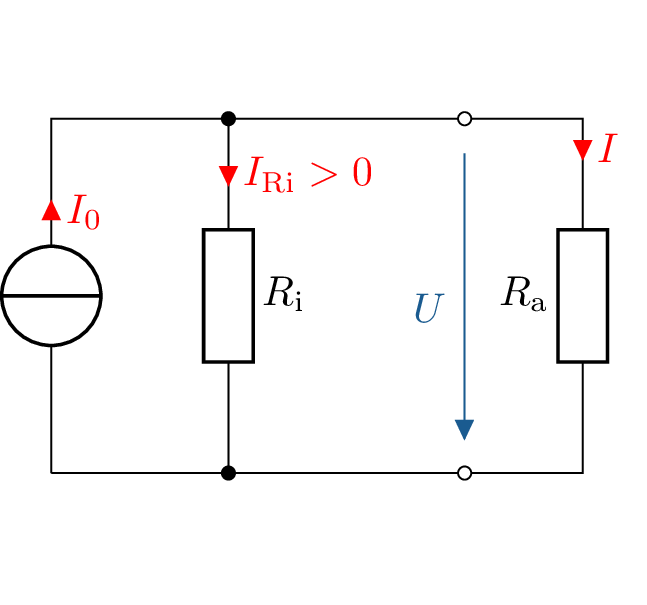
Auch eine reale Stromquelle besteht aus einer idealen Stromquelle \(U_0\) sowie einem Innenwiderstand \(R_\mathrm {i}\) (siehe Abbildung 14). Dieser ist im Gegensatz zur realen Spannungsquelle jedoch parallel anstatt in Reihe zur Quelle geschaltet.

Schematische Darstellung einer realen Stromquelle, bestehend aus einer idealen Stromquelle I0 und
einem parallel geschalteten Innenwiderstand Ri. Der Innenwiderstand leitet einen Strom IRi ¿ 0 ab,
während der Hauptstrom I über den Lastwiderstand Ra fließt. Die anliegende Spannung U fällt
zwischen den oberen und unteren Klemmen ab. — Abbildung 14: Aus einer idealen Stromquelle \(I_0\) und einem Innenwiderstand \(R_\mathrm {i}\) bestehende reale Stromquelle, welche mit einem Widerstand \(R_\mathrm {a}\) belastet ist

Abhängig von der sich einstellenden Ausgangsspannung \(U\) fließt durch den endlichen Innenwiderstand \(R_\mathrm {i}\) der Strom \(I_\mathrm {Ri} = U / R_\mathrm {Ri}\), der Ausgangsstrom \(I\) ergibt sich also zu

Merke: Ausgangsstrom einer realen Stromquelle

\begin {equation*} I = I_0 - \frac {U}{R_\mathrm {i}} \end {equation*}

Um die Reduktion den Ausgangsstroms \(I\) durch den Innenwiderstand zu reduzieren, sollte dieser möglichst groß gewählt werden:

\begin {equation*} I_0 >> \frac {U}{R_\mathrm {i}} \end {equation*}

Die Ersatzstromquelle

Alternativ zur Ersatzspannungsquelle kann ein aktiver Zweipol auch als Ersatzstromquelle dargestellt werden (Abbildung 15). Auch sie kann durch eine ideale Stromquelle \(I_0\) sowie einen zusammengefassten Innenwiderstand \(R_\mathrm {i}\) vollständig charakterisiert werden.

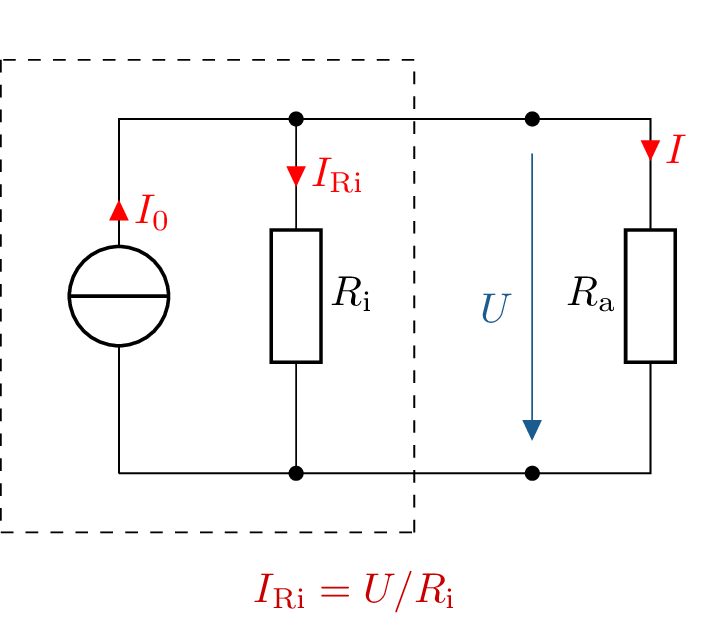
Darstellung einer Ersatzstromquelle, bestehend aus einer idealen Stromquelle I0 und einem parallel
geschalteten Innenwiderstand Ri. Der Innenwiderstand leitet den Strom IRi ab, der gemäß IRi =
U/Ri berechnet wird. Die anliegende Spannung U fällt über dem Lastwiderstand Ra ab. Der
gestrichelte Kasten markiert den Bereich der Ersatzstromquelle. — Abbildung 15: Die Ersatzstromquelle (gestrichelter Kasten) verfügt über das gleiche Ersatzschaltbild wie eine reale Stromquelle

Analog zur Ersatzspannungsquelle können auch hier die Parameter \(I_0\) sowie \(R_\mathrm {i}\) mit Hilfe des Leerlauf- und Kurzschlussversuchs bestimmt werden.

Beim Leerlaufversuch fließt der gesamte Strom \(I_0\) durch den Innenwiderstand. An den dazu parallel anliegenden Klemmen stellt sich die folgende Leerlaufspannung \(U_\mathrm {L}\) ein:

\begin {equation*} U_\mathrm {L} = R_\mathrm {i} \cdot I_0 \end {equation*}

Kennlinie einer Ersatzstromquelle. Auf der y-Achse ist die Stromstärke I(U), auf der x-Achse die
Spannung U dargestellt. Die rote Gerade fällt linear von I0 bei U = 0 bis auf 0 bei UL = I0 * Ri ab. — Abbildung 16: Die aus der Ersatzstromquelle herausfließende Stromstärke \(I\) in Abhängigkeit der sich einstellenden Spannung \(U\)

Beim Kurzschlussversuch werden die beiden Klemmen der Ersatzstromquelle kurzgeschlossen. Da die Spannung über dem Kurzschluss und somit auch über dem dazu parallelgeschalteten Innenwiderstand null Volt beträgt, fließt durch \(R_\mathrm {i}\) kein Strom.

Der gesamte Strom \(I_0\) fließt also durch den Kurzschluss:

Merke: Kurzschlussstrom einer Ersatzstromquelle

\begin {equation*} I_0 = I_\mathrm {K} \end {equation*}

Mit \(U_\mathrm {L} = R_\mathrm {i} \cdot I_0\) kann nun der Innenwiderstand bestimmt werden:

Merke: Innenwiderstand einer Ersatzstromquelle

\begin {equation*} R_\mathrm {i} = \frac {U_\mathrm {L}}{I_\mathrm {K}} \end {equation*}

5.3 Umwandlung von Spannungs- und Stromquellen

Bei der Netzwerkanalyse kann es sinnvoll sein, Stromquellen in Spannungsquellen oder Spannungsquellen in Stromquellen umzuwandeln. Dies funktioniert sowohl für reale Strom- bzw. Spannungsquellen, als auch für Ersatzstrom- bzw. Ersatzspannungsquellen identisch. Dabei bleibt der Wert des Innenwiderstandes \(R_\mathrm {i}\) identisch, seine Position im Ersatzschildbild ändert sich jedoch (siehe Abbildung 17)

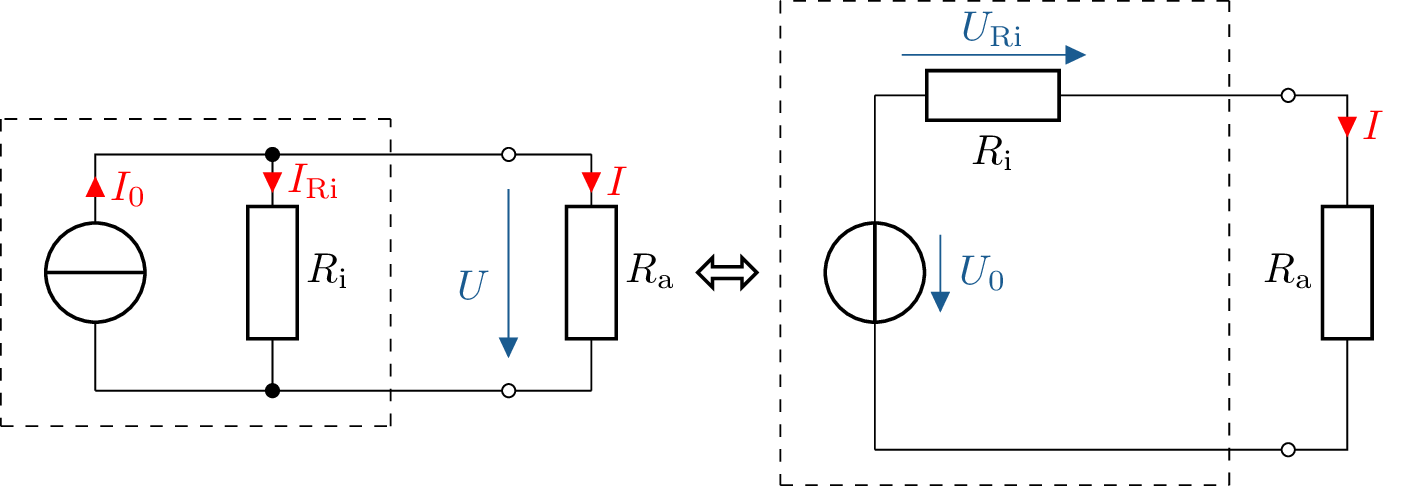
Darstellung der Umwandlung zwischen Ersatzstromquelle und Ersatzspannungsquelle. Links
befindet sich eine Ersatzstromquelle, bestehend aus einer idealen Stromquelle I0 und einem parallel
geschalteten Innenwiderstand Ri. Rechts ist die äquivalente Ersatzspannungsquelle dargestellt, die
aus einer idealen Spannungsquelle U0 und einem in Reihe geschalteten Innenwiderstand Ri besteht.
Beide versorgen denselben Lastwiderstand Ra. Die beiden Darstellungen sind durch ein
Doppelpfeilsymbol verbunden, welches die gegenseitige Austauschbarkeit der beiden Ersatzmodelle
verdeutlicht. — Abbildung 17: Umwandlung einer Ersatzstromquelle (links) in eine Ersatzspannungsquelle (rechts) und umgekehrt

Die Leerlaufspannung beziehungsweise der Kurzschlussstrom bleiben bei der Umwandlung der Quelle erhalten und werden auf die jeweils andere Quelle umgerechnet.

Achtung: Die Zählpfeile von ineinader umgewandelten Strom- und Spannungsquellen sind entgegengesetzt gerichtet!

Beim Umwandeln einer Stromquelle in eine Spannungsquelle beträgt die Spannung \(U_0\):

Merke: Spannung einer umgewandelten Spannungsquelle

\begin {equation*} U_0 = I_0 \cdot R_\mathrm {i} \end {equation*}

Die Stromstärke \(I_0\) beträgt beim Umwandeln einer Spannungsquelle in eine Stromquelle:

Merke: Strom einer umgewandelten Stromquelle

\begin {equation*} I_0 = \frac {U_0}{R_\mathrm {i}} \end {equation*}