Knoten- und Maschenanalyse
Bei der Betrachtung von elektrischen Netzwerken werden vor allem die Ströme in Knoten und die Spannungen in Maschen analysiert. Die Analyse von Knoten und Maschen in elektrischen Netzwerken erfolgt durch die beiden Kirchhoffsche Regeln.
Lernziele: Knoten- und Maschenanalyse
Die Studierenden
- 1.
- kennen die grundlegenden Definitionen zur Beschreibung eines elektrischen Netzwerkes.
- 2.
- können die Knotenregel und die Maschenregel auf elektrische Netzwerke anwenden.
1 Stromdichte im freien Raum
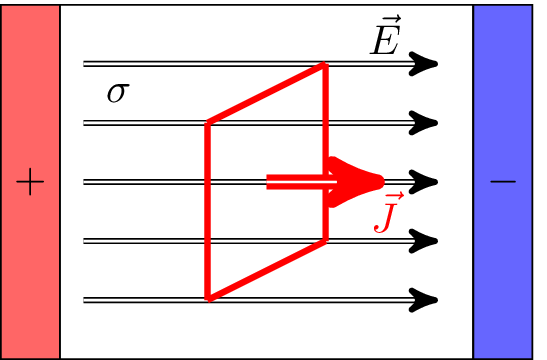
Gegebenheiten und Begriffe aus der Feldtheorie führen zu den Erklärungen im strukturierten Feldraum. Dazu werden in der Abbildung 1 eine positiv geladene Platte und eine negativ geladene Platte dargestellt, die sich gegenüberstehen. Der Raum zwischen den beiden Platten weist ein Elektrisches Feld \(\vec {E}\) und ein Medium mit der Leitfähigkeit \(\sigma \) auf. Ladungsträger können sich in dem freien Raum bewegen. Es stellt sich eine gerichtete Bewegung von Ladungsträgern und damit eine Stromdichte \(\vec {J}\) zwischen den Platten ein. Die Stromdichte ist dabei in der betrachteten Fläche quellenfrei.
Die Quellenfreiheit der Stromdichte wird durch die Gleichung 1 verdeutlicht. Hier wird beschrieben, dass keine Quellen oder Senken existieren, da sich keine feldbildenden Ladungen im Raum befinden. Für diesen Fall ist die Stromdichte quellenfrei und es fließen dieselbe Anzahl an Ladungen in die Fläche hinein und wieder heraus. Mathematisch wird dies für die Betrachtung im freien Raum in der Kontinuitätsgleichung ausgedrückt:
\begin {equation} \oint _{}^{} \vec {J} d\vec {A} = 0 \quad \rightarrow \quad div \vec {J} = 0 \label {divJQuellenfreiheit} \end {equation}
2 Stromdichte im strukturierten Raum
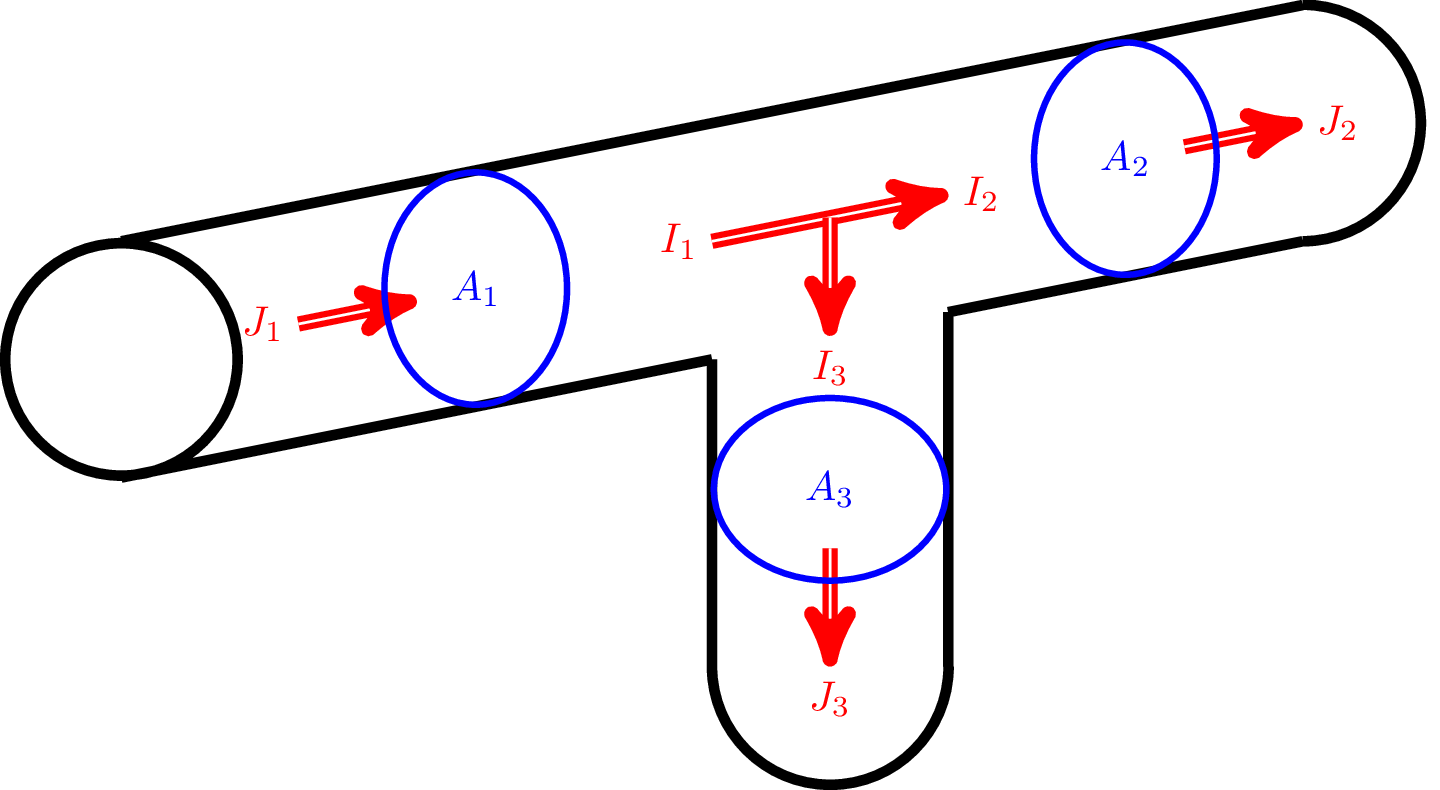
Im strukturierten Feldraum (vgl. Abbildung 2) gilt ebenfalls die Quellenfreiheit der Stromdichte. Alle Ladungen, die in den Feldraum eindringen, müssen ihn auch wieder verlassen. Dies gilt auch für den Fall, dass ein elektrischer Leiter mehr als einen Ableiter aufweist. Es wird eine Zuleitung mit zwei Ableitungen angedeutet, bei dem sich die Ladungen auf die beiden Ableitungen aufteilen. Die Zylinder-Mantelflächen \(A_1\), \(A_2\) und \(A_3\) definieren mit den angrenzenden Zylindern einen strukturierten Feldraum. Wie die Ladungen teilen sich die Stromdichten durch den strukturierten Raum auf. So ergibt sich die Stromdichte \(\vec {J_1}\) aus der Summe der abfließenden Stromdichten \(\vec {J_2}\) und \(\vec {J_3}\).
Da der Feldraum im Beispiel durch die Flächen strukturiert und der Querschnitt der Leitung definiert ist, lassen sich aus der Beziehung zwischen der Stromdichte und der Fläche die Ströme der Leitungen gemäß Gleichung 2 ermitteln.
\begin {equation} I_1 = \iint _{A}^{} \vec {J_1} d\vec {A} \label {GleichungStromberechnung} \end {equation}
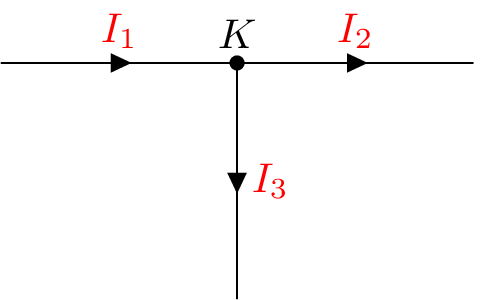
Der Zusammenhang der Stromdichten zueinander lässt sich so auf die Ströme übertragen. Der Strom der Zuleitung \(I_1\) ergibt sich aus der Summe der beiden Ableitungsströmen \(I_2\) und \(I_3\). Der Beispielleiter kann auch als vereinfachtes elektrisches Netzwerk dargestellt werden. Die ermittelten Ströme um den Verbindungspunkt K (Knoten) werden in der Abbildung 3 abgebildet.
3 Exkurs: Graphentheorie
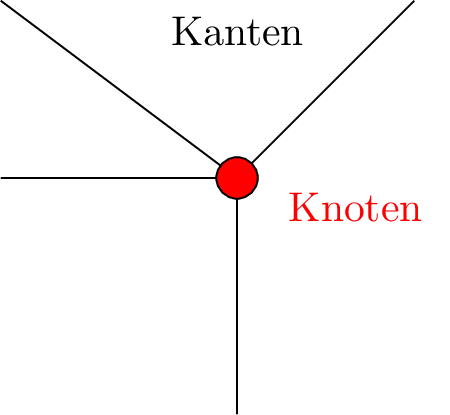
In der Mathematik beschäftigt sich die Graphentheorie mit der Beschreibung von Knoten und Kanten, in der Kontenanalyse werden ebenfalls Knoten und Äste definiert. Durch die Graphentheorie können die Kanten und Knoten, welche in der Abbildung 4 dargestellt werden, sowie deren Eigenschaften miteinander in Beziehung gesetzt werden. Über die Kanten können mehrere Knoten miteinander verbunden werden.
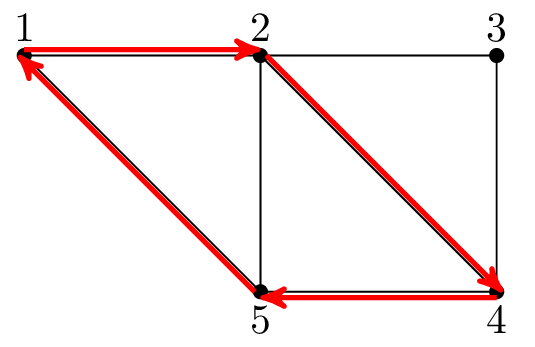
Werden mehrere Knoten mit ihren Kanten miteinander verbunden entsteht ein Graph. Mit diesem Graph kann exemplarisch ein elektrisches Netzwerk beschrieben werden. Das Beispiel eines Netzwerkes mit fünf Knoten und den zwischen den Knoten liegenden Kanten wird in der Abbildung 5 gezeigt. Wird ein Weg durch das Netzwerk gesucht ergeben sich unterschiedliche Möglichkeiten. Ein Weg vom Knoten 1 über die Knoten 2, 4 und 5 zurück zum Knoten 1 wird rot hinterlegt. Sind Anfang und Ende derselbe Knoten, so wird dieser Weg in der Graphentheorie auch als Zyklus bezeichnet. Jeder Zyklus, bei dem jeder Knoten bis auf den Anfang und das Ende nur einmal „besucht“ wird, nennt man einen „Kreis“. In elektrischen Netzwerken werden diese Kreise auch als Maschen bezeichnet.
Um die Beziehung der Knoten untereinander zu erklären bietet sich in der Mathematik eine Matrix an. Die Knoten weisen eine differenzierte Anzahl von Kanten auf und nicht alle Knoten sind miteinander verbunden. Die Adjazenz-Matrix beschreibt die Beziehung der Knoten untereinander. Eine solche Adjazenz-Matrix wird in der Gleichung 3 für das beschriebene Beispielnetzwerk aufgestellt. Sie beschreibt damit vollständig den Graphen, abgesehen von der grafischen Repräsentanz in der 2D-Darstellung.
\begin {equation} A = \begin {bmatrix} \color {blue}{1} & 1 & 0 & 0 & 1\\ 1 & \color {blue}{1} & 1 & 1 & 1\\ 0 & 1 & \color {blue}{1} & 1 & 0\\ 0 & 1 & 1 & \color {blue}{1} & 1\\ 1 & 1 & 0 & 1 & \color {blue}{1} \end {bmatrix} \label {AdjazenzMatrix} \end {equation}
Merke: Graphentheorie
In der Graphentheorie werden Netzwerke mit Kanten und Knoten beschrieben. Bei der Analyse der Netzwerke werden Wege und Zyklen definiert. Ein durchgehender Zyklus mit einem identischen Startpunkt und Endpunkt wird als Kreis bezeichnet.
4 Knoten, Zweig, Masche
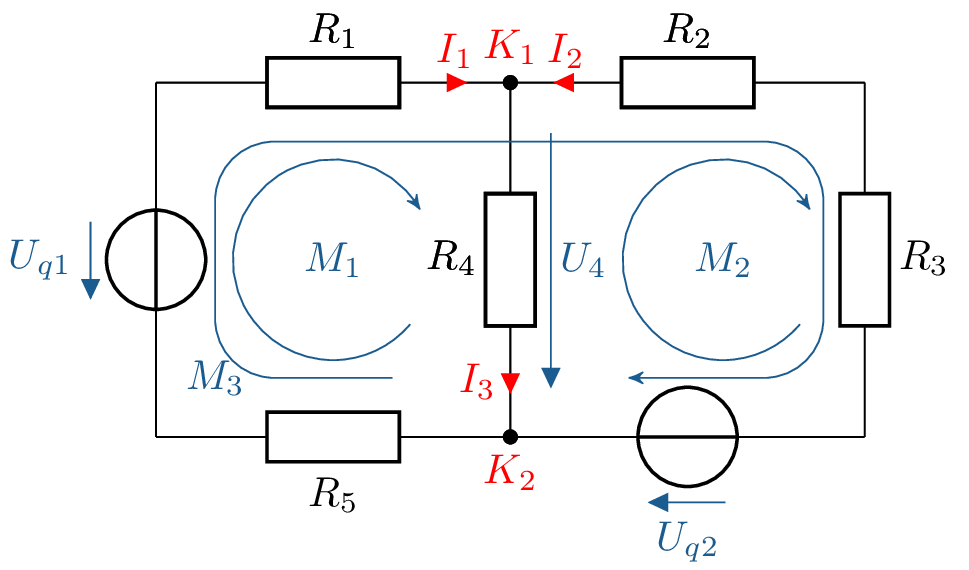
Ein elektrisches Netzwerk besteht aus Knoten, Zweigen und Maschen. Ein Zweig verbindet genau zwei Knoten durch ein oder mehrere Schaltungselemente miteinander. Durch alle Elemente eines Zweiges fließt der gleiche Strom. In Abbildung 6 existieren drei Zweige. Ein Zweig mit den Komponenten \(R_1\), \(R_5\) und \(U_\mathrm {q1}\), ein Zweig mit dem Widerstand \(R_4\) und ein Zweig mit den Komponenten \(R_2\), \(R_3\) und \(U_\mathrm {q2}\).
Ein Knoten ist ein Punkt, an dem mindestens drei Anschlüsse der Schaltungselemente zusammenlaufen. Der Strom kann sich hier also aufteilen. Das elektrische Potential ist hierbei für alle verbundenen Anschlüsse identisch. Im Schaltplan wird ein Knoten durch einen ausgefüllten Kreis gekennzeichnet. Sind jedoch zwei oder mehrere dieser Kreise nur durch eine Leitung miteinander verbunden, handelt es sich um einen einzigen Knoten, da das Potential auch hier gleich ist. Ein Knoten wird mit \(K_n\) bezeichnet.
Eine Masche ist ein geschlossener Weg, der aus mindestens zwei Zweigen besteht. In dem Netz in Abbildung 6 können drei Maschen definiert werden:
- \(M_1\) bestehend aus \(R_1\), \(R_4\), \(R_5\) und \(U_\mathrm {q1}\)
- \(M_2\) bestehend aus \(R_2\), \(R_3\), \(R_4\) und \(U_\mathrm {q2}\)
- \(M_3\) bestehend aus \(R_1\), \(R_2\), \(R_3\), \(U_\mathrm {q2}\), \(R_5\) und \(U_\mathrm {q1}\)
Eine Masche wird mit \(M_\mathrm {n}\) bezeichnet. Die Umlaufrichtung ist dabei von Bedeutung und wird mit einem Pfeil gekennzeichnet.
Merke: Knoten, Zweige und Maschen
Elektrische Netzwerke werden analog zur Graphentheorie durch Knoten, Zweige und Maschen beschrieben.
5 Der vollständige Baum
Für die weitere Analyse des Netzwerkes ist es notwendig, die Netzwerkgleichungen zu ermitteln. Dieses lineare Gleichungssystem ist aber immer überbestimmt, weshalb es nötig wird, die Anzahl der Gleichungen zu reduzieren. Dabei ist es wichtig, die linear abhängigen Gleichungen zu identifizieren und zu eliminieren.
Die Knoten, Zweige und Maschen eines Netzwerkes können in einem Graph dargestellt werden, der nur die Verbindungen untereinander darstellt. Zur Darstellung des Graphen werden alle Zweige als Linien dargestellt, welche die Knoten verbinden. Der Inhalt des Zweiges ist dafür irrelevant. In Abbildung 7 ist ein beispielhaftes Netz mit dem sich ergebenden Graphen dargestellt.
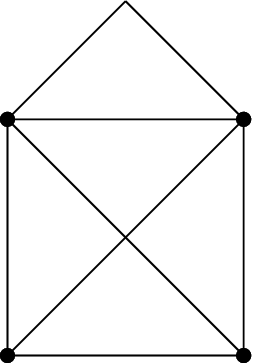
In diesem Graph kann ein vollständiger Baum aufgezeichnet werden, der alle Knoten enthält, aber selbst keine Masche bildet. Die Baumzweige verbinden also alle Knoten miteinander, bilden aber keine geschlossene Linie. Die Baumzweige können Abzweigungen bilden, ein Knoten kann also auch mehr als zwei Baumzweige berühren. In größeren Netzwerken gibt es mehrere Möglichkeiten für einen vollständigen Baum, die prinzipiell gleichwertig sind. Bei der Vorstellung der verschiedenen Berechnungsverfahren werden aber abhängig vom Verfahren bestimmte Kombinationen bevorzugt. Ein vollständiger Baum beinhaltet genau \(k-1\) Zweige.
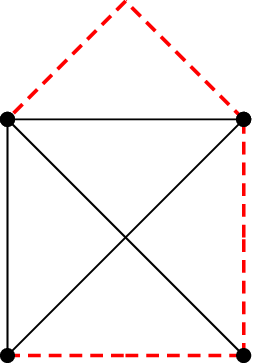
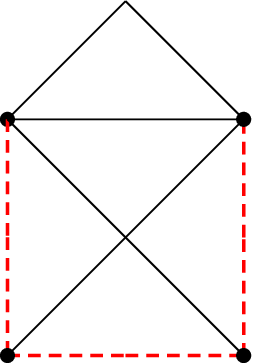
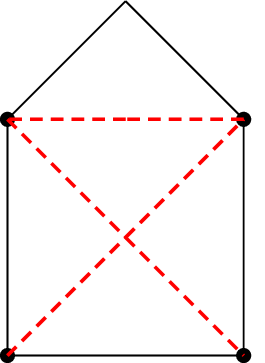
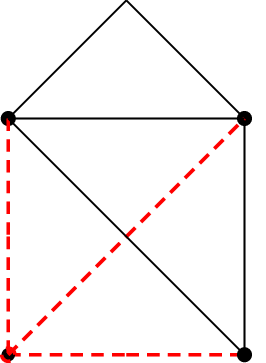
Die Zweige, die zum Baum gehören, werden Baumzweige (rot), die anderen Verbindungszweige (schwarz) genannt. Um die linear unabhängigen Maschen zu finden, wird zu jedem Verbindungszweig eine Masche gebildet, die außer dem Verbindungszweig nur Baumzweige enthält.
- Ein Netzwerk mit \(z\) Zweigen und \(k\) Knoten enthält \(z-k+1\) Verbindungszweige.
Merke: Der vollständige Baum
Mithilfe eines vollständigen Baumes werden alle Knoten miteinander durch Baumzweige verbunden. Es ergeben sich dabei immer k - 1 Baumzweige. Der vollständige Baum bildet keine Masche.
6 Knotenregel
Treffen sich mehr als zwei Leitungen an einem Punkt eines elektrischen Netzwerkes handelt es sich um einen Knotenpunkt K. Die Pfeilrichtung aus der Sicht des Knotens bestimmt das Vorzeichen des Stromes. Führt ein Strom in einen Knoten hinein, so zeigt der Strompfeil auf den Knoten und es handelt sich um eine Einströmung. Zeigt der Strompfeil aus dem Knoten heraus, wird der Strom aus dem Knoten herausgeführt und es handelt sich um eine Ausströmung. Die Knotenanalyse ergibt sich aus dem 1. Kirschhoff‘schen Gesetz, welches besagt: Die Summe aller Ströme an einem Knoten ist Null (Gleichung 4). Dieses Gesetz folgt direkt aus der Kontinuitätsgleichung (vgl. Abschnitt Stromdichte im freien Raum)
\begin {equation} \sum _{k = 1}^{N}{I_\mathrm {k} = 0} \label {Knotenregel} \end {equation}
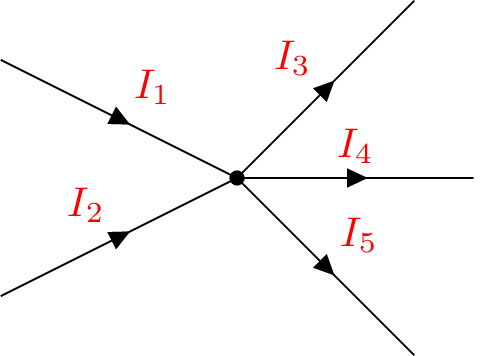
So müssen sich für jeden Knoten die Summe der Stromstärken aus Einströmungen und Ausströmungen gegenseitig ausgleichen. In der Abbildung 9 sind ein Knoten K und die Ein- und Ausströmungen eingezeichnet. Bei den Strömen \(I_1\) und \(I_2\) handelt es sich um Einströmungen. Die drei Ströme \(I_3\), \(I_4\) und \(I_5\) sind Ausströmungen.
Werden die Ströme nacheinander aufgetragen und gleich Null gesetzt, ergibt sich die Gleichung 5. Je nachdem ob es sich um eine Einströmung oder eine Ausströmung handelt, wird das Vorzeichen gewählt. Einströmungen werden mit einem positiven und Ausströmungen mit einem negativen Vorzeichen behaftet.
\begin {equation} \sum _{k = 1}^{N}{I_\mathrm {k}} =0=I_1+I_2-I_3-I_4-I_5 \label {KnotenregelBeispielknoten} \end {equation}
Merke: Knotenregel
7 Maschenregel
Bewegt sich ein Teilchen zwischen zwei Punkten in einem elektrischen Feld, wird Arbeit verrichtet. Ist der Startpunkt identisch mit dem Endpunkt, muss ebenso viel Arbeit abgegeben wie aufgenommen werden. Die Summe der Arbeit ist in diesem Fall gleich Null. Wenn so ein kompletter Maschenumlauf entlang einer geschlossenen Strecke vollzogen wird, muss die Summe der Teilspannungen ebenfalls gleich Null sein. Vorausgesetzt wird hier, dass sich keine zeitlich veränderte magnetische Flussdichte ergibt und somit kein elektrisches Wirbelfeld entsteht (vgl. Gleichung 7). Die Gleichung beschreibt hier das Faradaysche Induktionsgesetz für statische Felder (hier: keine Änderung eines Magnetfeldes).
\begin {equation} \oint _{s}^{} \vec {E} d\vec {s} = 0 \quad \rightarrow \quad rot \vec {E} = 0 \label {GleichungRingintegralFeldstärke} \end {equation}
Die Maschenanalyse besagt nach der 2. Kirchhoffschen Regel, dass bei einem vollständigen Umlauf (Masche) in einem elektrischen Netzwerk die Summe aller Spannungen gleich Null ist. Dies wird durch die Gleichung 8 verdeutlicht.
\begin {equation} \sum _{k = 1}^{N}{U_\mathrm {k}} =0 \label {Maschenregel} \end {equation}
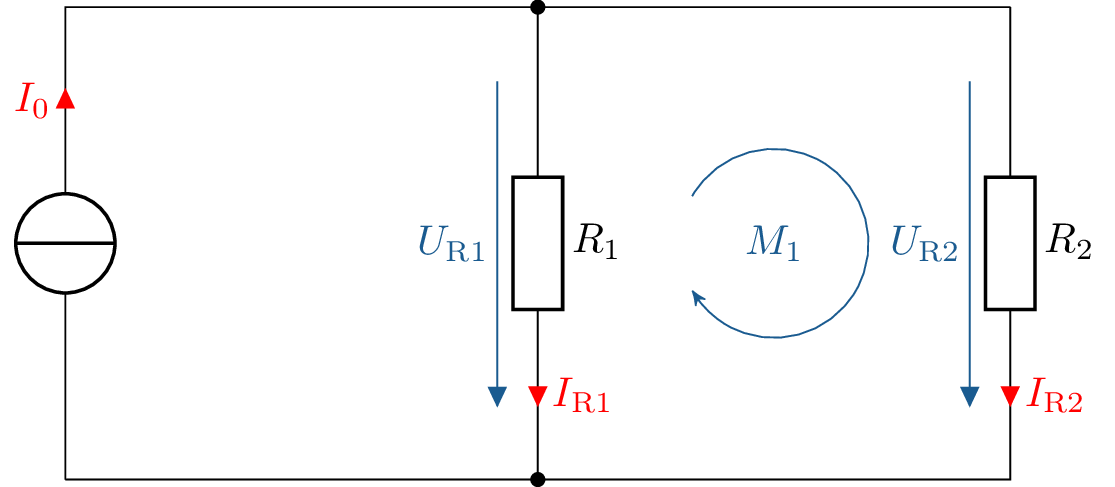
Innerhalb einer Masche werden die Spannungen mit einer gleichgerichteten Pfeilrichtung positiv gezählt, Spannungen mit der Umlaufrichtung entgegengesetzten Pfeilrichtung werden negativ gezählt. Ausgehend von den Stromverläufen und Potentialen aus der Abbildung 10 können die Spannungen der jeweiligen Zweige ermittelt werden. Oberhalb der Parallelschaltung der Widerstände gibt es keine Potentialdifferenz. Selbiges gilt für die elektrische Verbindung unterhalb der Parallelschaltung. Der Strom \(I_\mathrm {R1}\) fließt durch den Widerstand \(R_\mathrm {1}\). So ergibt sich nach dem ohmschen Gesetz die Spannung \(U_\mathrm {R1}\) über \(R_\mathrm {1}\). Äquivalent wird die Spannung \(U_\mathrm {R2}\) über \(R_\mathrm {2}\) bestimmt.
Gemäß des vorgestellten Netzwerkes und der Richtung der eingezeichneten Masche \(M_\mathrm {1}\) stellt sich der Zusammenhang nach Gleichung 9 ein. Die Spannung \(U_\mathrm {R2}\) verläuft in derselben Richtung, wie die eingezeichnete Masche und wird mit einem positiven Vorzeichen behaftet. Die Spannung \(U_\mathrm {R1}\) verläuft gegenläufig der Masche \(M_\mathrm {1}\) und wird somit negativ. In Summe müssen diese beiden Spannungen null ergeben.
\begin {equation} \sum _\mathrm {k = 1}^{N}{U_\mathrm {k}} \onslide <3->{= + U_\mathrm {R2}} \onslide <4->{- U_\mathrm {R1}} \onslide <5->{=0} \label {Maschengleichung} \end {equation}
Merke: Maschenregel
8 Knoten- und Maschenanalyse
Bei der Knoten- und Maschenanalyse wird das vollständige Gleichungssystem bestehend aus Knoten- und Maschengleichungen aufgestellt und anschließend gelöst. Das Verfahren ist einfach, erzeugt jedoch für ein Netzwerk eine Anzahl Gleichungen, die der Anzahl der Zweige entspricht. Das Verfahren hat den folgenden Ablauf:
- 1.
- Vereinfachen des Netzwerkes.
- 2.
- Einzeichnen aller Strompfeile und Erstellen des Graphen.
- 3.
- Aufstellen von \(k-1\) Knotengleichungen. Eine beliebige Knotengleichung kann weggelassen werden, da in einem Netzwerk mit \(k\) Knoten nur \(k-1\) Knotengleichungen linear unabhängig voneinander sind. Prinzipiell ist es egal, welche Knotengleichung unberücksichtigt bleibt. Am geschicktesten wird die komplizierteste Gleichung gestrichen.
- 4.
- Aufstellen der \(m=z-k+1\) linear unabhängigen Maschengleichungen. Dabei werden die Gleichungen mit Hilfe des vollständigen Baumes erstellt.
- 5.
- Lösen des Gleichungssystems mit der Dimension \(z\).
- 6.
- Ggfs. rückgängig machen von Schritt 1.
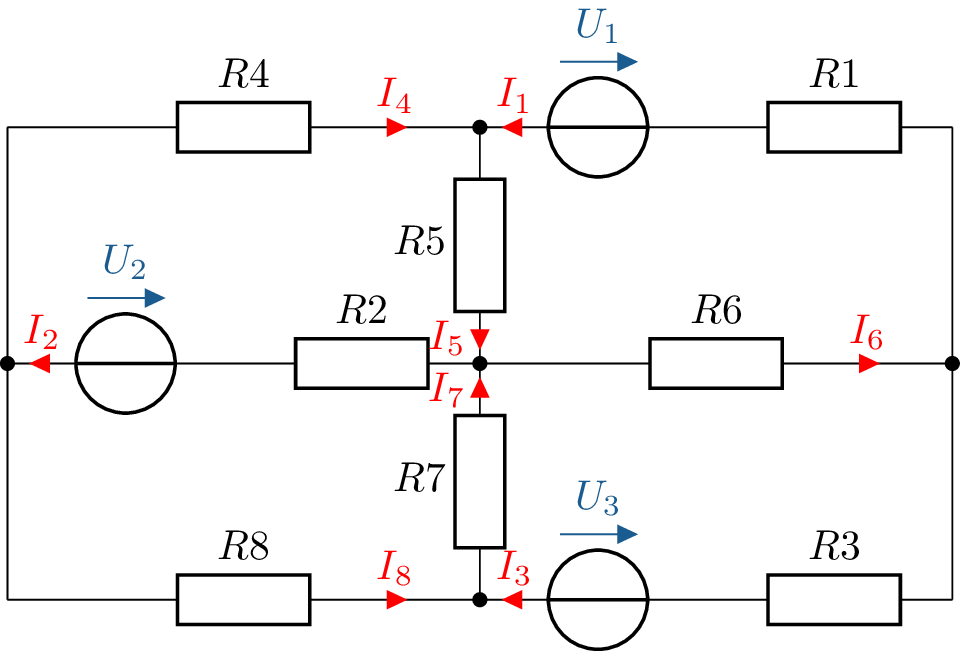
Es wird folgendes Beispielnetzwerk betrachtet:
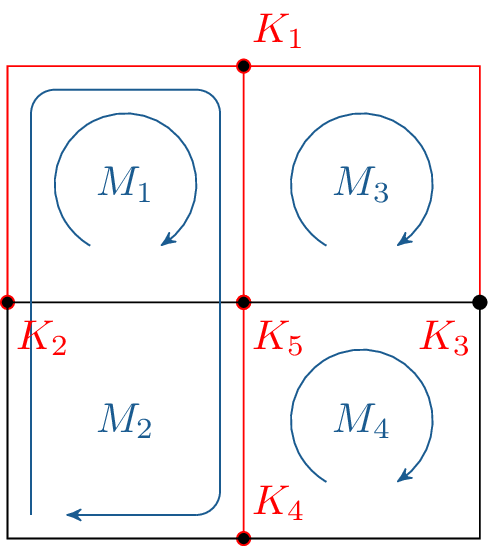
Der zugehörige Graph und die damit festgelegten Maschen werden in der Abbildung 12 dargestellt. Eine andere Aufstellung der Maschen ist möglich. Wie gezeigt, können Maschen auch über Zweige hinaus reichen.
Das Netzwerk hat \(z=8\) Zweige, \(k=5\) Knoten. Es müssen daher \(k-1=4\) Knotengleichungen und \(z-k+1=4\) Maschengleichungen aufgestellt werden. Knoten 5 hat vier Zweige, die anderen nur drei. Daher wird die Knotengleichung von Knoten 5 weggelassen.
\begin {align*} \only <1>{K_1:\qquad & I_1+I_4-I_5=0\\ K_2:\qquad & I_2-I_4-I_8=0\\ K_3:\qquad & -I_1-I_3+I_6=0\\ K_4:\qquad & I_3-I_7+I_8=0\\} \only <2>{M_1:\qquad & R_2I_2 + R_4I_4 + R_5I_5 - U_{2} = 0\\ M_2:\qquad & R_4I_4 + R_5I_5 - R_7I_7 - R_8I_8 = 0\\ M_3:\qquad & -R_1I_1 - R_5I_5 - R_6I_6 + U_{1} = 0\\ M_4:\qquad & R_3I_3 + R_6I_6 + R_7I_7 - U_{3} = 0} \end {align*}
Um das Gleichungssystem einfacher lösen zu können, und die Übersichtlichkeit zu erhöhen, kann es in Matrizenschreibweise dargestellt werden. Mit etwas Übung kann auch sofort die Matrizenschreibweise benutzt werden.
\begin {equation*} \left [\begin {array}{cccccccc} 1&0&0&1&-1&0&0&0\\ 0&1&0&-1&0&0&0&-1\\ -1&0&-1&0&0&1&0&0\\ 0&0&1&0&0&0&-1&1\\ 0&R_2&0&R_4&R_5&0&0&0\\ 0&0&0&R_4&R_5&0&-R_7&-R_8\\ -R_1&0&0&0&-R_5&-R_6&0&0\\ 0&0&R_3&0&0&R_6&R_7&0 \end {array}\right ] \cdot \left (\begin {array}{c} I_1\\I_2\\I_3\\I_4\\I_5\\I_6\\I_7\\I_8 \end {array}\right ) = \left (\begin {array}{c} 0\\0\\0\\0\\U_{2}\\0\\-U_{1}\\U_{3} \end {array}\right ) \end {equation*}
Dieses Gleichungssystem 8. Ordnung kann nun prinzipiell mit den aus der Mathematik bekannten Verfahren gelöst werden. Das wollen wir aber hier nicht tun, da im folgenden einfachere Verfahren vorgestellt werden, die besser zu berechnen sind.
Beispiel 1: Netzwerkanalyse
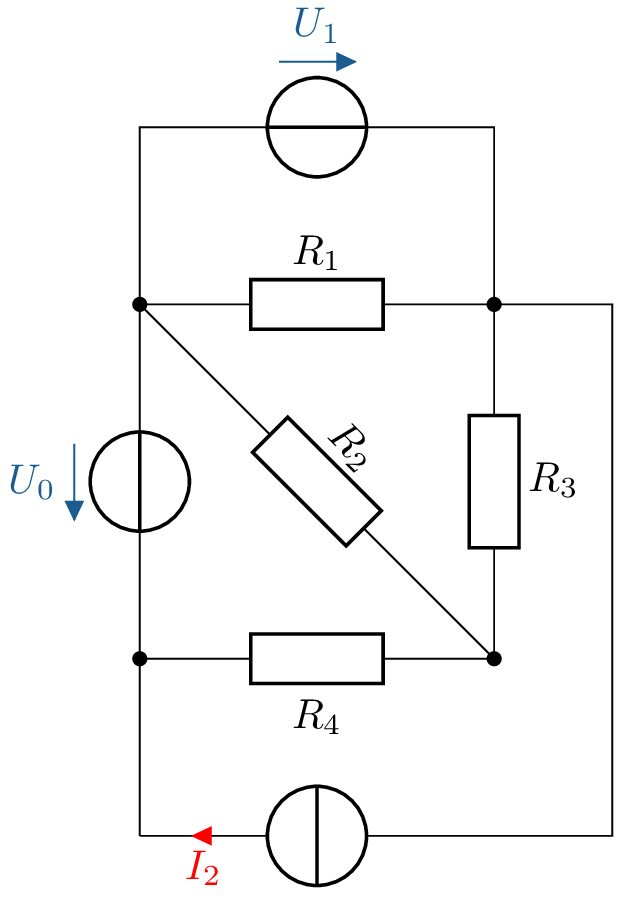
Gegeben ist das elektrische Netzwerk nach Abbildung 13. Die folgenden Aufgaben sollen bearbeitet werden:
-
- a)
- Einzeichnen der Ströme und Spannungen
- b)
- Aufstellen der Knotengleichungen
- c)
- Aufstellen der Maschengleichung \(M_1\)
- d)
- Aufstellen der Maschengleichung \(M_2\) ohne den Ausdruck \(U_1\)
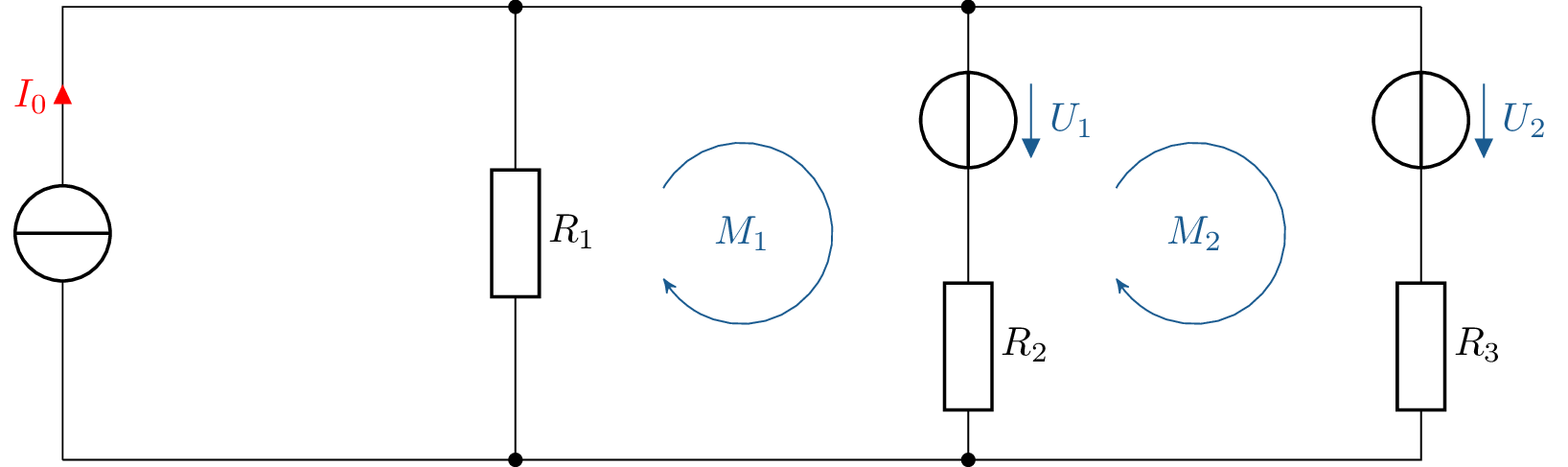
Abbildung 13: Beispiel. Netzwerkanalyse mit Kirchhoffschen Regeln. - a)
- Angabe der Ströme und Spannungen:
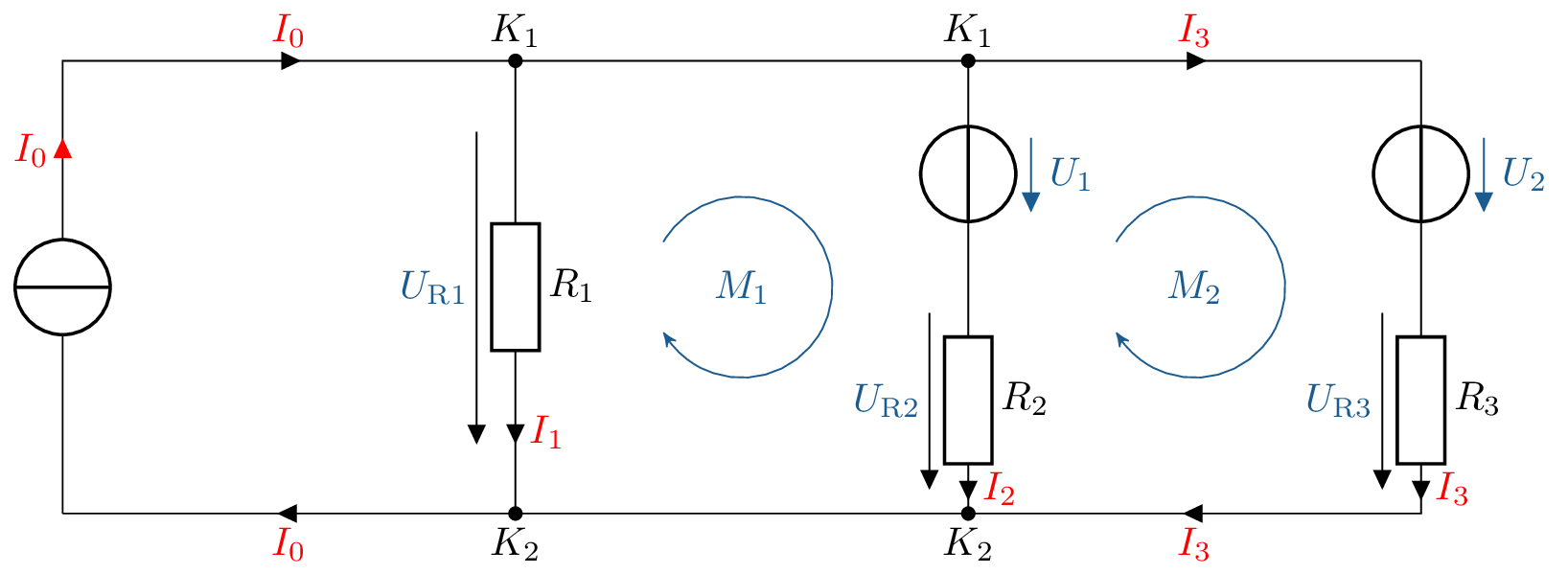
- b)
- Knotengleichungen: \begin {align} K_1: I_0-I_1-I_2-I_3&=0 \nonumber \\ K_2: -I_0+I_1+I_2+I_3&=0 \nonumber \end {align}
- c)
- Aufstellen der Maschengleichung \(M_1\) und \(M_2\): \begin {align} M_1: U_1+U_\mathrm {R2}-U_\mathrm {R1}&=0 \nonumber \\ M_2: U_2+U_\mathrm {R3}-U_\mathrm {R2}-U_1&=0 \nonumber \end {align}
- d)
- Aufstellen der Maschengleichung \(M_2\) ohne den Ausdruck \(U_1\) \begin {align} M_1: U_1&=U_\mathrm {R1}-U_\mathrm {R2} \nonumber \\ M_2: U_2+U_\mathrm {R3}-U_\mathrm {R2}-(U_\mathrm {R1}-U_\mathrm {R2})&=0 \nonumber \\ M_2: U_2+U_\mathrm {R3}-\cancel {U_\mathrm {R2}}-U_\mathrm {R1}+\cancel {U_\mathrm {R2}}&=0 \nonumber \\ M_2: U_2+U_\mathrm {R3}-U_\mathrm {R1}&=0 \nonumber \end {align}
...