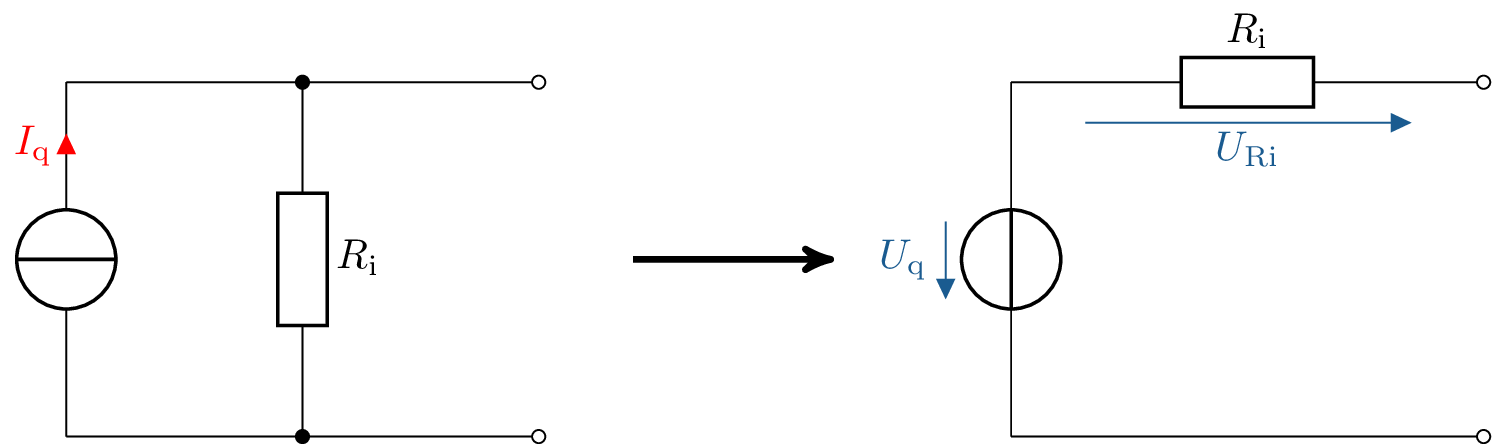Lernziele: Maschenstromverfahren
Die Studierenden
- kennen die Schritte des Maschenstromverfahrens.
- können mit Hilfe des Maschenstromverfahrens elektrische Netzwerke analysieren.
Maschenstromverfahren
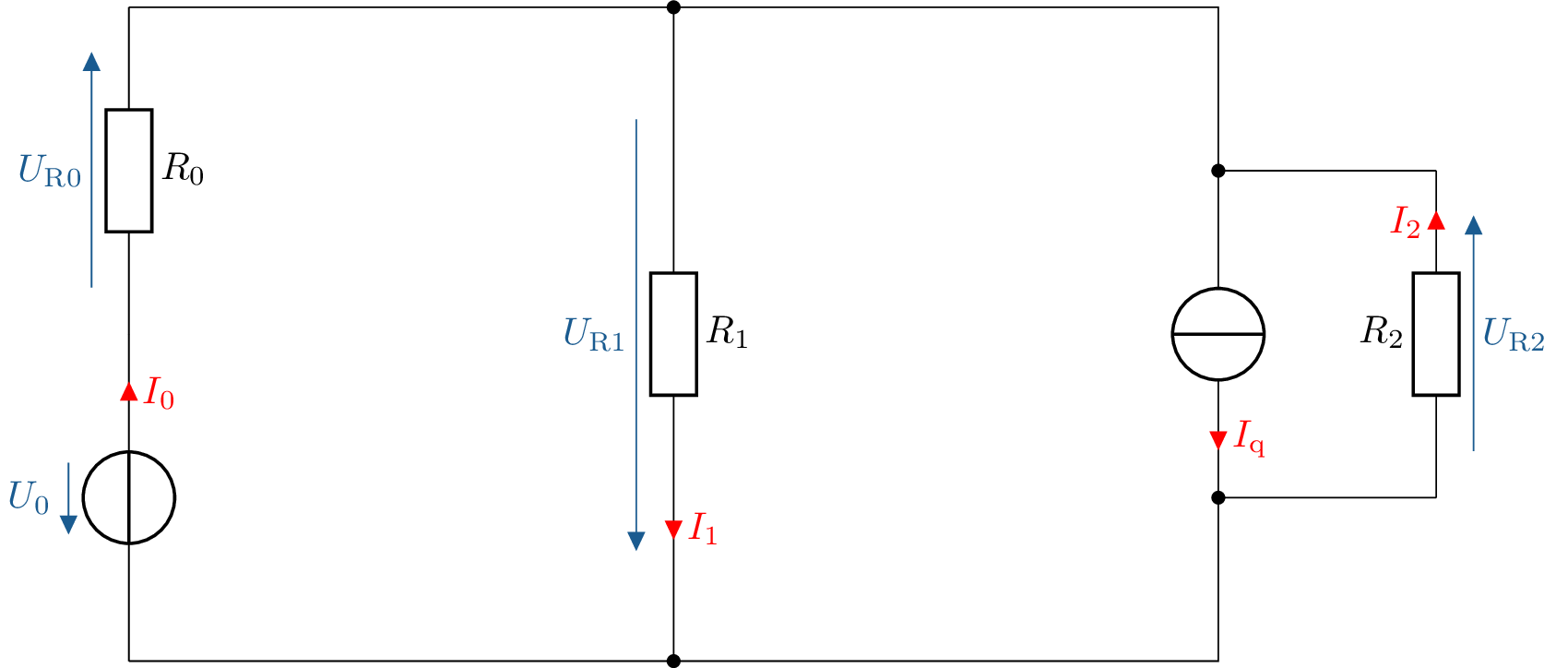
Neben der Knotenpotentialanalyse zur Untersuchung von elektrischen Netzwerken kann auch das Maschenstromverfahren zur Berechnung herangezogen werden. Beim Maschenstromverfahren wird ein Gleichungssystem aufgestellt, mit welchem die Maschenströme ermittelt werden können. Um das Gleichungssystem des Maschenstromverfahrens aufstellen zu können, müssen einige Vorbereitungen getroffen werden. In den folgenden Schritten soll das elektrische Netzwerk aus der Abbildung 1 mittels des Maschenstromverfahrens berechnet werden.
1 Vorbereitung des Netzwerkes
Das Maschenstromverfahren arbeitet mit Spannungsquellen und Widerstandswerten. Hierfür müssen eventuelle Stromquellen in Spannungsquellen transformiert werden. Diese Art der Umwandlung einer Stromquelle in eine Spannungsquelle wird noch einmal in der Abbildung 2 dargestellt. Hier wird aus der Stromquelle und dem parallel liegenden Innenwiderstand eine Spannungsquelle mit einem in reihe liegenden Innenwiderstand.
Die Gleichung 1 zeigt die Berechnung des Spannungswertes der Spannungsquelle aus dem angegebenen Stromwert der Stromquelle und dem Widerstandswert des Innenwiderstands.
\begin {equation} U_\mathrm {q} = R_\mathrm {i} \cdot I_\mathrm {q} \label {GleichungUmrechnungStromquelle} \end {equation}
Außerdem müssen mögliche Leitwerte von elektrischen Widerständen in Widerstandswerte geändert werden. In der Gleichung 2 wird gezeigt, wie der Widerstandswert aus dem Kehrwert des Leitwerts ermittelt wird.
\begin {equation} R_\mathrm {i} = \frac {1}{G_\mathrm {i}} \label {GleichungUmrechnungLeitwert} \end {equation}
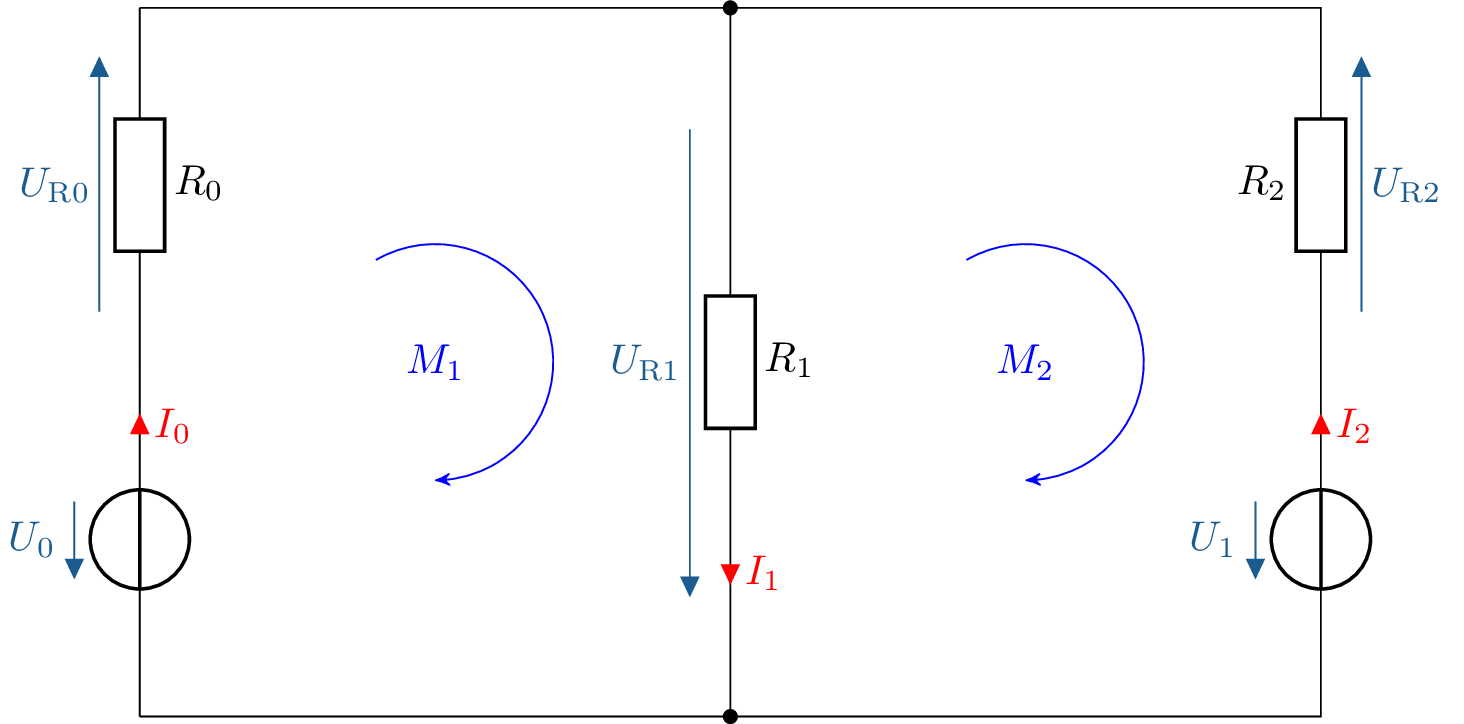
In der Abbildung 3 wird die Umwandlung der Stromquelle des vorgestellten Netzwerkes in eine Spannungsquelle durchgeführt. Aus der Parallelschaltung der Stromquelle und des Widerstandes \(R_2\) wird eine Reihenschaltung bestehend aus der neuen Spannungsquelle und dem Widerstand \(R_2\).
Merke: Maschenstromverfahren
Für das Maschenstromverfahren werden zur Analyse eines elektrischen Netzwerkes Spannungsquellen und Widerstandswerte benötigt.
2 Maschen definieren
Für die Maschenstromanalyse müssen die Maschen festgelegt werden. Über den Maschen werden die Maschenströme festgelegt. Außerdem werden den Maschen die Widerstände zugeordnet. In der Abbildung 4 wird das vorgestellte Netzwerk mit den eingezeichneten Maschen \(M_1\) und \(M_2\) dargestellt.
Durch alle Komponenten welche sich an der Masche \(M_1\) befinden, fließt der Maschenstrom \(I_\mathrm {M1}\). So wie auch alle Komponenten an der Masche \(M_2\) von dem Maschenstrom \(I_\mathrm {M2}\) durchflossen werden. Die beiden Maschenströme \(I_\mathrm {M1}\) und \(I_\mathrm {M2}\) werden vektoriell in der Gleichung 3 notiert.
\begin {equation} I_\mathrm {M} = \begin {bmatrix} I_\mathrm {M1} \\ \\ I_\mathrm {M2} \\ \end {bmatrix} \label {GleichungMaschenströme} \end {equation}
3 Widerstandsmatrix bestimmen
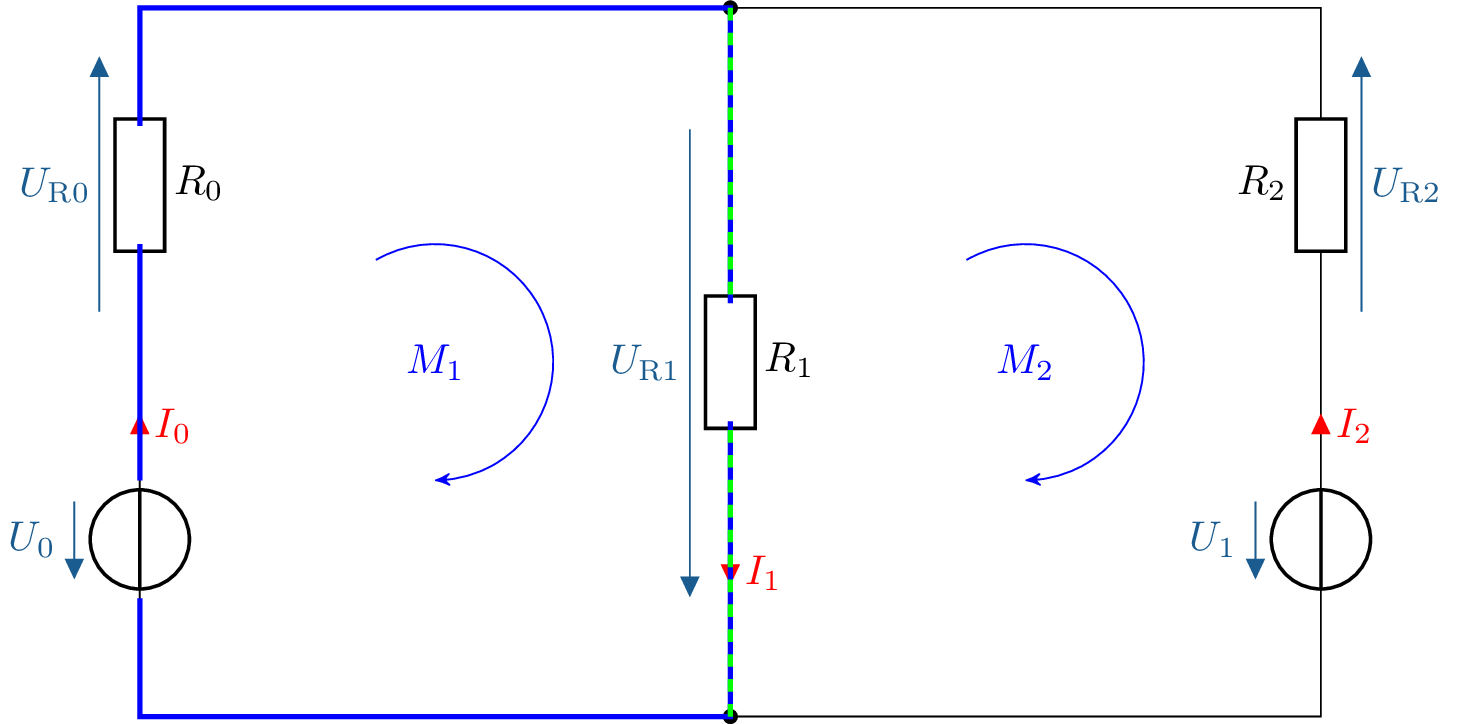
In der Masche \(M_1\) trifft der Maschenstrom \(I_{M1}\) auf die beiden Widerstände \(R_0\) und \(R_1\). Die Masche \(M_1\) wird in der Abbildung 5 in blau dargestellt. Der Maschenstrom \(I_{M2}\) der Masche \(M_2\) durchfließt die Widerstände \(R_1\) und \(R_2\). Der Widerstand \(R_1\) ist somit teil der beiden Maschen \(M_1\) und \(M_2\) und wird von beiden Maschenströmen durchflossen. Wird ein Widerstand von mehreren Maschenströmen durchflossen gilt dieser als Kopplungswiderstand zwischen den Maschen.
In der Widerstandsmatrix nach Gleichung 4 werden die Widerstände der Maschen und die Kopplungswiderstände zugeordnet. Hier werden die Umlaufwiderstände aus den Maschen in die Hauptdiagonale eingetragen. Das heißt, dass die Reihenschaltung \(R_0 + R_1\) das Element der ersten Spalte und Zeile für die erste Masche wird. Die Reihenschaltung \(R_1 + R_2\) wird in das Element der zweiten Spalte und Zeile für die zweite Masche eingetragen. In die übrigen Elemente der Widerstandsmatrix werden die Kopplungswiderstände zwischen den jeweiligen Maschen eingetragen. Der Kopplungswiderstand bekommt ein positives Vorzeichen, wenn beide Maschenströme in die selbe Richtung fließen und ein negatives, wenn diese entgegengesetzt fließen. Die Widerstandsmatrix wird in der Wechselstromtechnik auch als Maschenimpedanzmatrix bezeichnet.
\begin {equation} R_\mathrm {M} = \begin {bmatrix} \color {blue}{R_0 + R_1} & \color {green}{-R_1} \\ \\ \color {green}{-R_1} & R_1 + R_2 \\ \end {bmatrix} \label {GleichungWiderstandsmatrix} \end {equation}
4 Quellenspannungen zuordnen
Den Maschen müssen die Spannungsquellen, die sogennanten Quellspannungen zugeordnet werden. In der Masche \(M_1\) liegt die Quellenspannung \(U_0\). Die Masche \(M_2\) weist die Quellenspannung \(U_1\) auf. Bei übereinstimmender Richtung von Spannungspfeil und Maschenrichtung ergibt sich ein negatives Vorzeichen für die Quellspannungen. Sind die Richtungen von Spannungspfeil und dem Maschenumlauf entgegengesetzt wird das Vorzeichen der Quellspannung positiv. Für den Fall, dass in einer Masche keine Quelle vohanden ist, wird eine \(0\) eingetragen.
\begin {equation} U_\mathrm {M} = \begin {bmatrix} U_0 \\ \\ -U_1 \\ \end {bmatrix} \label {GleichungQuellspannungen} \end {equation}
5 Gleichungssystem aufstellen
Nach dem ohmschen Gesetz wird die elektrische Spannung als Produkt aus dem elektrischen Widerstand und Strom berechnet. Bei der Maschenstromanalyse werden zur Berechnung des Vektors der Maschenströme \(I_\mathrm {M}\) die Widerstandsmatrix \(R_\mathrm {M}\) und der Vektor der Quellspannungen \(U_\mathrm {M}\) verwendet. Das Gleichungssystem wird in der Gleichung 6 abgebildet.
\begin {equation} \begin {bmatrix} R_0 + R_1 & -R_1 \\ \\ -R_1 & R_1 + R_2 \\ \end {bmatrix} \cdot \begin {bmatrix} I_\mathrm {M1} \\ \\ I_\mathrm {M2} \\ \end {bmatrix} = \begin {bmatrix} U_0 \\ \\ -U_1 \\ \end {bmatrix} \label {GleichungMasche1} \end {equation}
Die gesuchte Größen werden aus den Maschenströmen berechnet. Beispielsweise werden die Ströme \(I_0\), \(I_1\) und \(I_2\) gesucht. Die Ergebnisse der Maschenströme sind mit den Strömen gleichzusetzen, welche lediglich von einem Maschenstrom durchflossen werden. In dem vorgestellten elektrischen Netzwerk beträgt der Strom der Masche \(M_1: I_\mathrm {M1} = I_0\) und der Masche \(M_2: I_\mathrm {M2} = -I_2\). Der Strom durch den Widerstand \(R_1\) lässt sich beispielsweise über die Knotengleichung berechnen: \(I_1 = I_0 + I_2\).
Beispiel 1: Maschenstromverfahren
Analyse des elektrischen Netzwerk aus der Abbildung 6 mittels der Maschenstromanalyse.
-
Für die Maschenstromanalyse sollen die folgenden Schritte bearbeitet werden:
- Vorbereitung des Netzwerkes
- Maschen und Maschenströme definieren
- Widerstandsmatrix bestimmen
- Quellspannungen zuordnen
- Gleichungssystem aufstellen
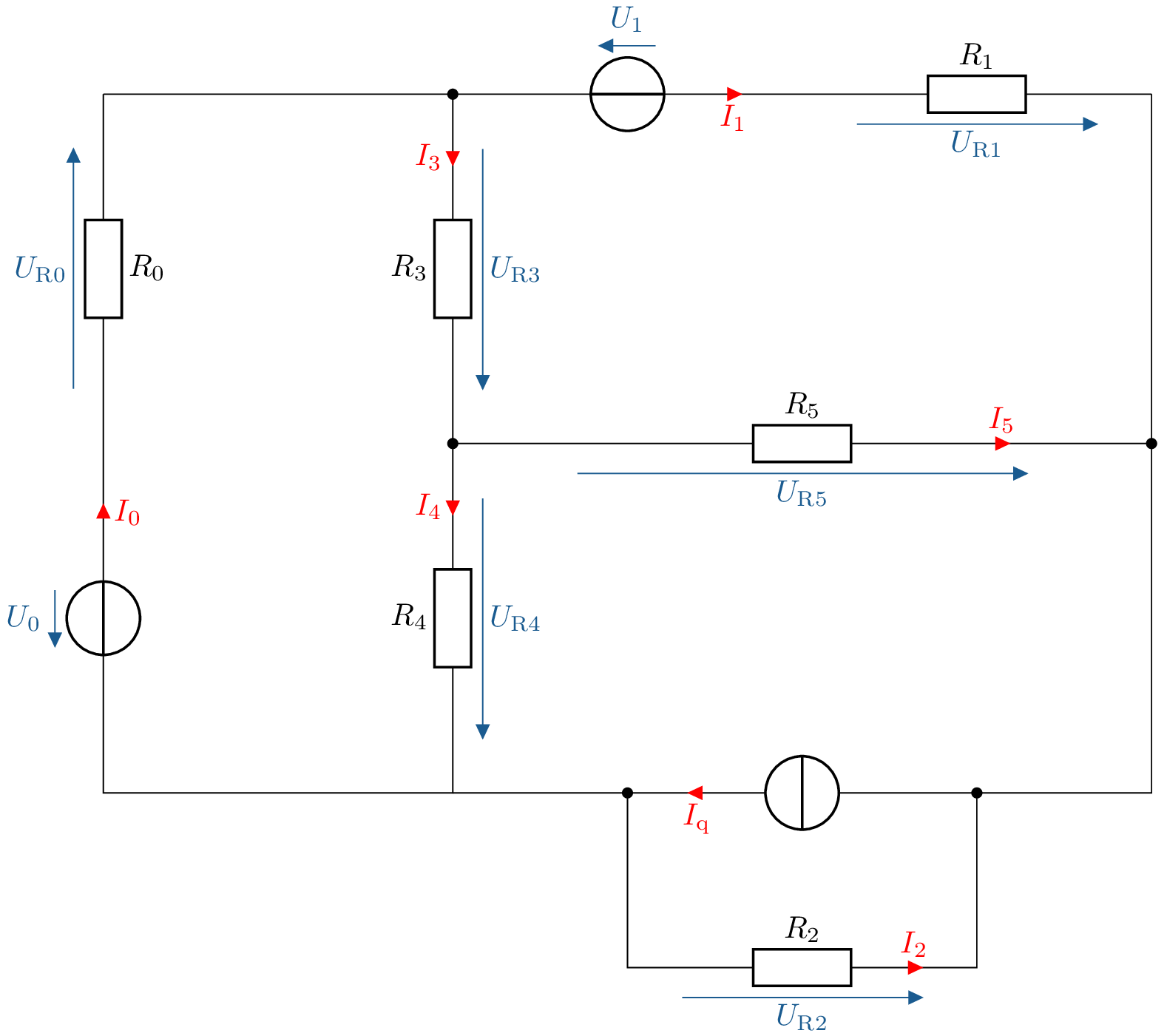
Abbildung 6: Beispiel. Maschenstromanalyse an einem elektrischen Netzwerk. - a)
- Vorbereitung des Netzwerkes:
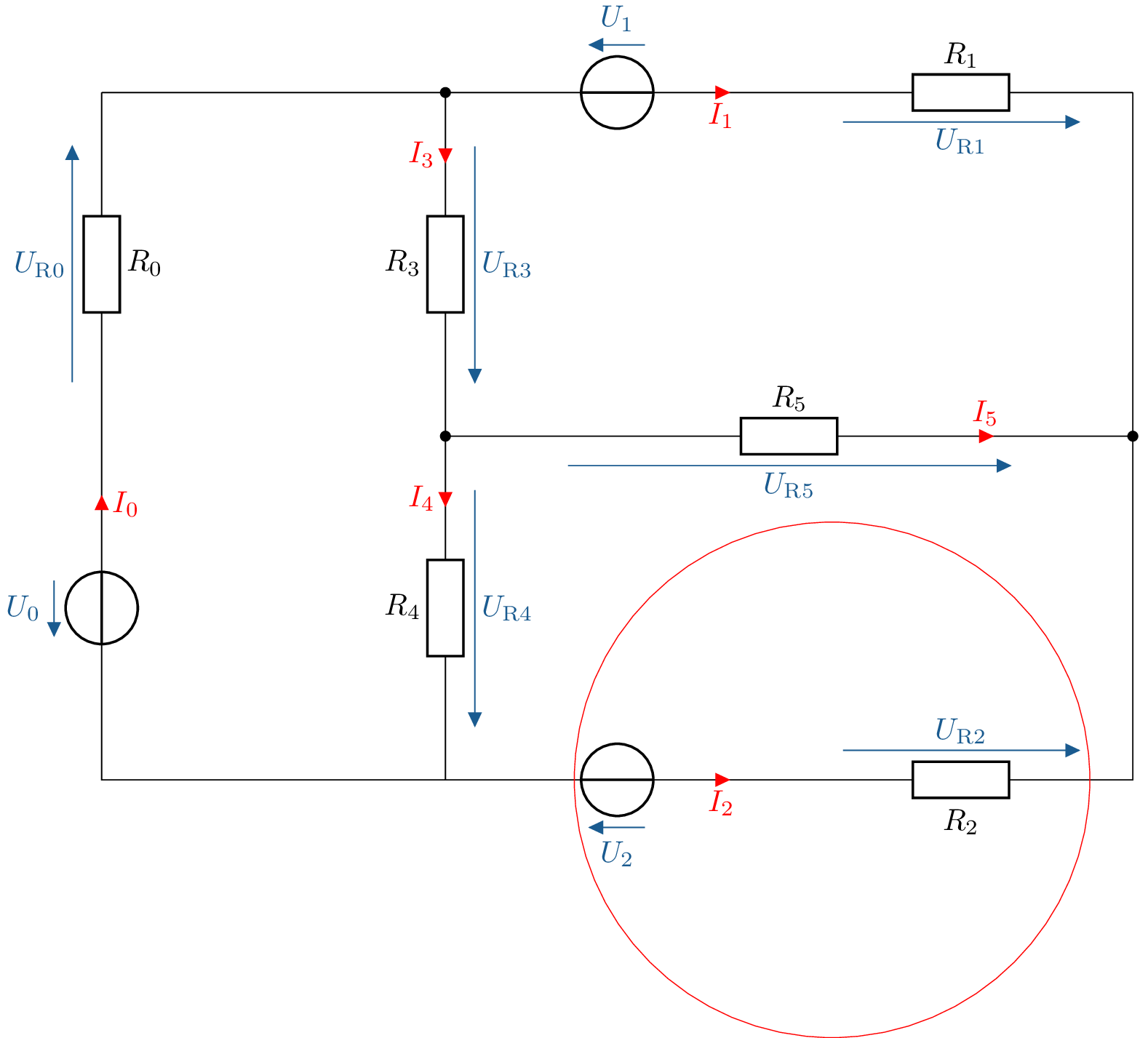
- b)
- Maschen und Maschenströme definieren:
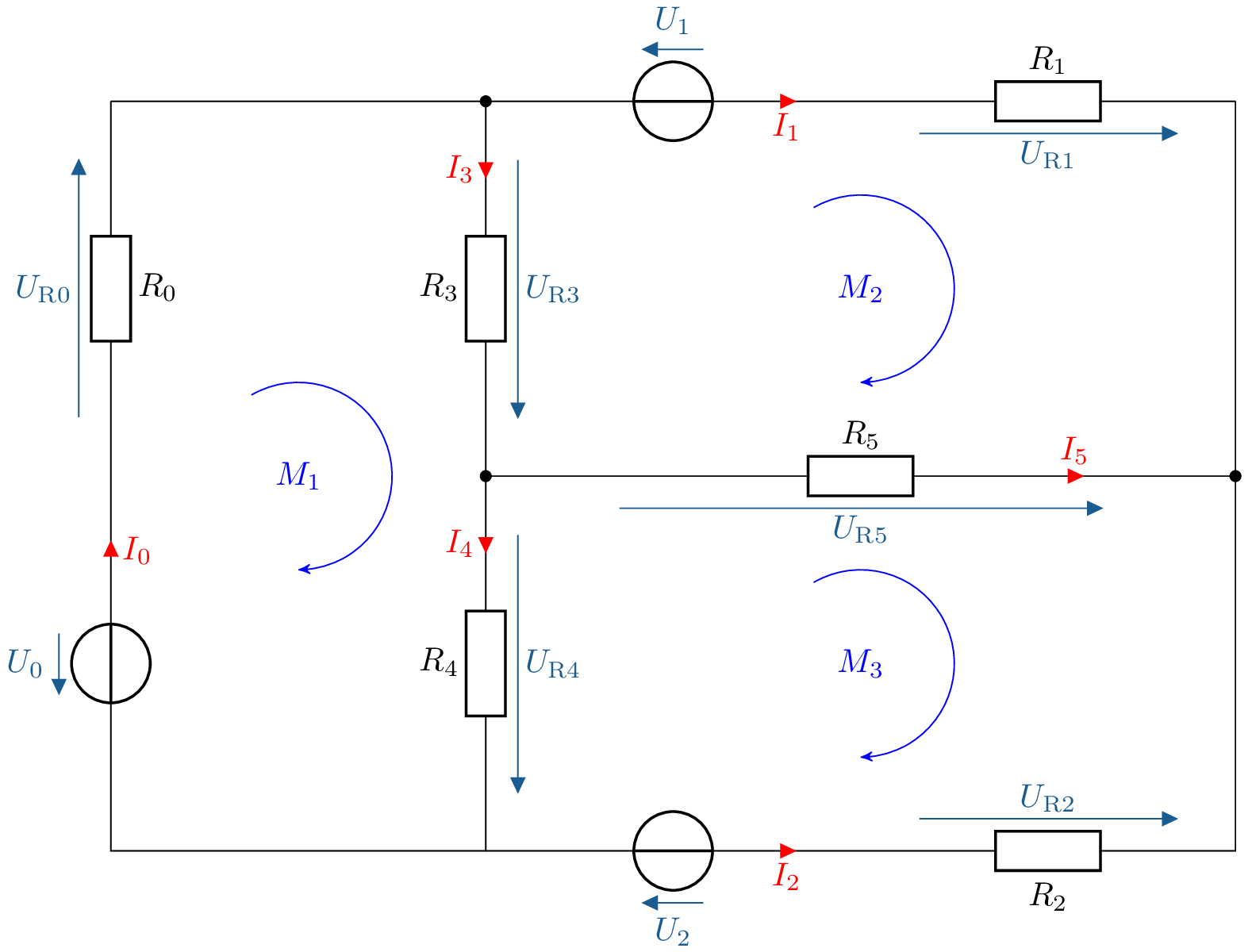
\begin {equation} I_\mathrm {M} = \begin {bmatrix} I_\mathrm {M1} \\ \\ I_\mathrm {M2} \\ \\ I_\mathrm {M3} \\ \end {bmatrix}\nonumber \end {equation}
- c)
- Widerstandsmatrix bestimmen: \begin {equation} R_\mathrm {M} = \begin {bmatrix} R_0 + R_3 + R_4 & -R_3 & -R_4 \\ \\ -R_3 & R_1 + R_3 + R_5 & -R_5\\ \\ -R_4 & -R_5 & R_2 + R_4 + R_5 \\ \end {bmatrix} \nonumber \end {equation}
- d)
- Quellspannungen zuordnen: \begin {equation} U_\mathrm {M} = \begin {bmatrix} U_0 \\ \\ U_1 \\ \\ -U_2\\ \end {bmatrix} \nonumber \end {equation}
- e)
- Gleichungssystem aufstellen: \begin {equation} \begin {bmatrix} R_0 + R_3 + R_4 & -R_3 & -R_4 \\ \\ -R_3 & R_1 + R_3 + R_5 & -R_5\\ \\ -R_4 & -R_5 & R_2 + R_4 + R_5 \\ \end {bmatrix} \cdot \begin {bmatrix} I_\mathrm {M1} \\ \\ I_\mathrm {M2} \\ \\ I_\mathrm {M3} \\ \end {bmatrix} = \begin {bmatrix} U_0 \\ \\ U_1 \\ \\ -U_2\\ \end {bmatrix}\nonumber \end {equation} Ströme Berechnen: \begin {align} I_3 = I_0 - I_1\nonumber \\ I_4 = I_3 - I_5\nonumber \\ I_0 = I_4 - I_2\nonumber \\ -I_5 = I_2 + I_1\nonumber \end {align}
...