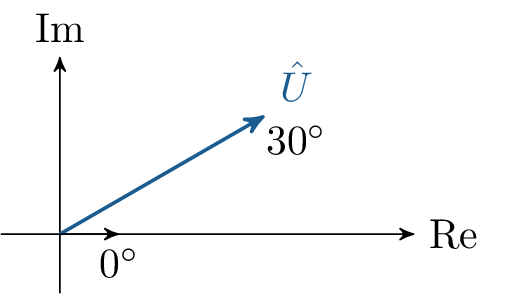1 Komplexe Zahlen 1
Es gelte für folgende komplexe Zahlen:
\(Z_1 = 3+j4\)
\(Z_2 = 2-j\)
\(Z_3 = j7\)
Berechnet werden sollen folgende Aufgabenteile:
- \(Z_1 + Z_2\)
- \(Z_1 - Z_3\)
- Polarform von \(Z_1\), \(Z_2\) und \(Z_3\)
- \(Z_1 \cdot Z_2\)
- \(\frac {Z_1}{Z_3}\)
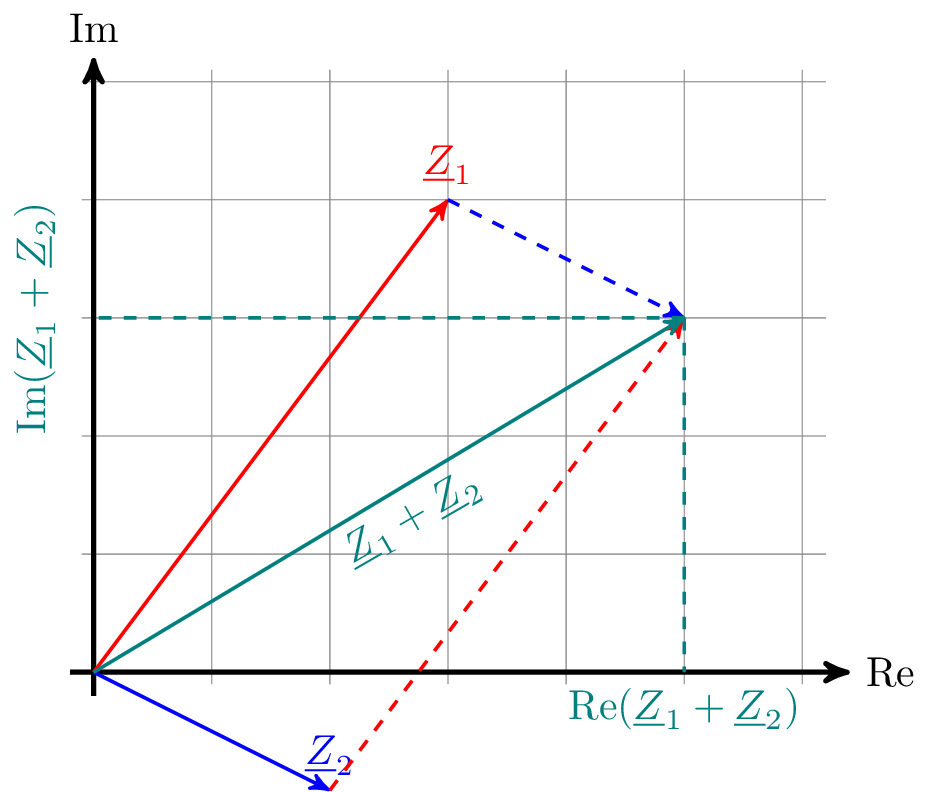
- Zeigerdiagramm von \(Z_1 + Z_2\) und \(Z_1 \cdot Z_2\)
1.1 Lösung:
- \(Z_1 + Z_2\)
\begin {align} Z_1 + Z_2 &= (3 + j4) + (2 - j) \nonumber \\ &= 5 + j3 \nonumber \end {align} -
\(Z_1 - Z_3\)
\begin {align} Z_1 - Z_3 &= (3 + j4) - (0 + j7) \nonumber \\ &= 3 - j3 \nonumber \end {align}
-
Polarform von \( Z_1, Z_2\) und \(Z_3 \)
\begin {align} Z_1 &= 5 \cdot \mathrm {e}^{\mathrm {j}53.13^\circ } \nonumber \\ Z_2 &= 2,236 \cdot \mathrm {e}^{\mathrm {j}-26,57^\circ } \nonumber \\ Z_3 &= 7 \cdot \mathrm {e}^{\mathrm {j}90^\circ } \nonumber \end {align}
-
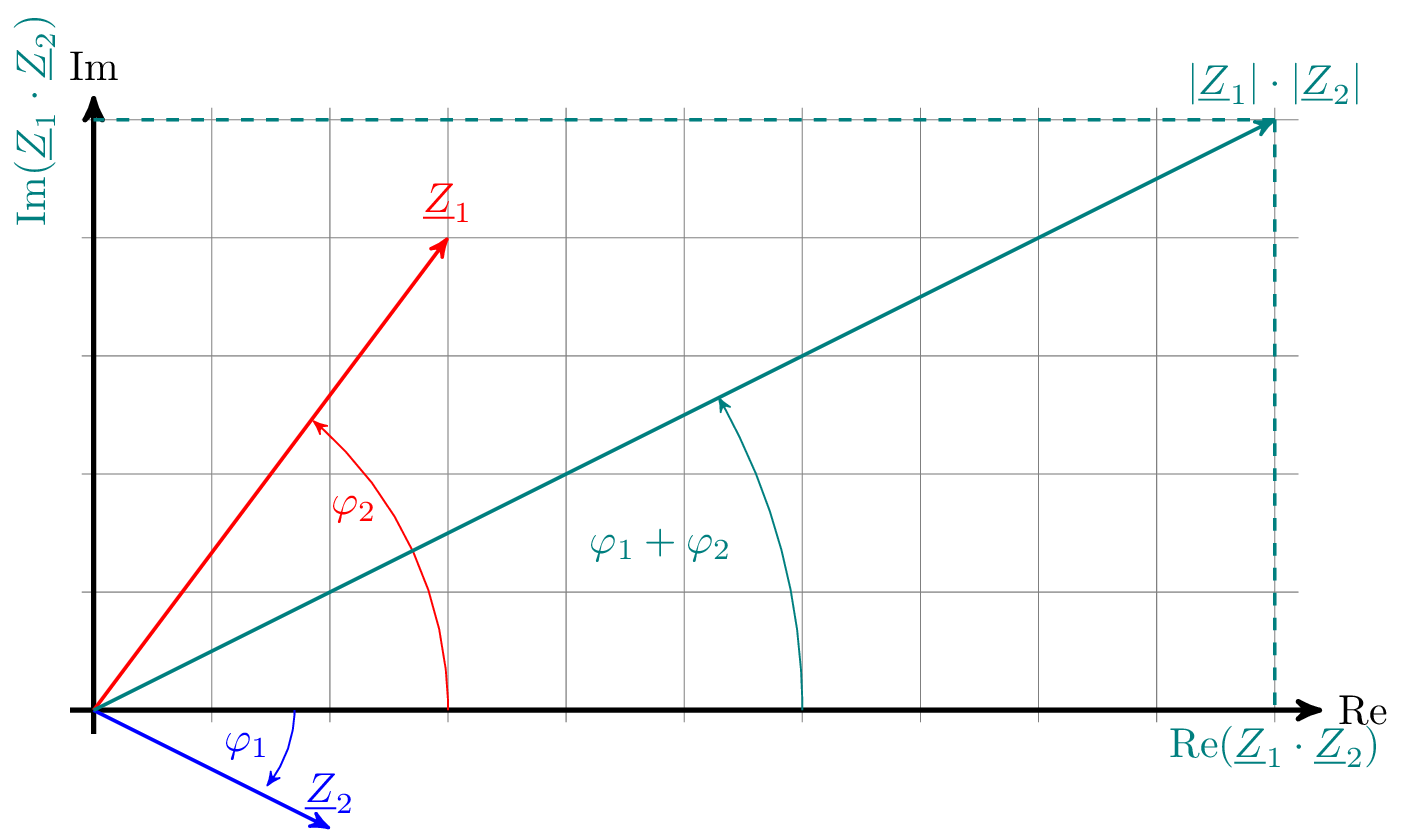
\(Z_1 \cdot Z_2\)
\begin {align} Z_1 \cdot Z_2 &= (3 + j4) \cdot (2 - j) \nonumber \\ &= 10 + j5 \nonumber \end {align}
-
\(\frac {Z_1}{Z_3} \)
\begin {align} \frac {Z_1}{Z_3} = \frac {3 + j4}{j7} \nonumber \end {align}
(Erweitern mit dem konjugierten Wert des Nenners, also -j7)
\begin {align} \frac {3 + j4}{j7} \cdot \frac {-j7}{-j7} = \frac {(3 + j4) \cdot (-j7)}{(j7) \cdot (-j7)} \nonumber \end {align}
Hinweis: \(j^2 = -1\)
\begin {align} \frac {Z_1}{Z_3} &= \frac {28 - j21}{49} = \frac {28}{49} - j \frac {21}{49} = \frac {4}{7} - j \frac {3}{7} \nonumber \\ &= \frac {4}{7} - j \frac {3}{7} \nonumber \end {align}
-
Zeigerdiagramm von \(Z_1 + Z_2 \) und \(Z_1 \cdot Z_2 \)
![s Bild zeigt ein komplexes Zeigerdiagramm mit Real- und Imaginärachse. Es wird die
Addition zweier komplexer Zahlen ZYou may provide a definition with und ZYou may
provide a definition with gezeigt, wobei der Summenvektor ZYou may provide a definition
with + ZYou may provide a definition with sowie seine Real- und Imaginärteile markiert
sind.]()
![Das Bild zeigt ein komplexes Zeigerdiagramm mit Real- und Imaginärachse. Es wird die
Multiplikation zweier komplexer Zahlen dargestellt, bei der sich die Beträge multiplizieren und die
Winkel You may provide a definition withYou may provide a definition with und You may provide a
definition withYou may provide a definition with addieren.]()
2 Komplexe Zahlen 2
Es gelte für folgende komplexe Zahlen:
\(K_1 = 10 + j40\)
\(K_2 = 50 \cdot e^{-j40^o}\)
\(K_3 = 250 \cdot e^{j\frac {\pi }{4}}\)
Berechnet werden sollen folgende Aufgabenteile:
- \(K_1 - K_2\), Ergebnis in Polarkoordinaten
- \(K_3 + K_2\), Ergebnis in kartesischen Koordinaten
- \(K_1 \cdot K_3\), Ergebnis in Polarkoordinaten
- \(K_1 + K_2\), zeichnerisch im Zeigerdiagramm
- \((K_1 - K_2)^2\)
- \(\sqrt {K_1 + K_3}\)
2.1 Lösung:
-
\(K_1 - K_2\), Ergebnis in Polarkoordinaten
\begin {align} 10 + \mathrm {j} \cdot 40 - 50 \cdot \mathrm {e}^{-\mathrm {j}40^\circ } = ? \nonumber \end {align}
\(\underline {K}_2\) in kartesische Koordinaten wandeln:
\begin {align} 50 \cdot \mathrm {e}^{-\mathrm {j}40^\circ } &= 50 \cdot \cos (-40^\circ ) + \mathrm {j} 50 \cdot \sin (-40^\circ ) \nonumber \\ &= 50 \cdot 0,766 + \mathrm {j} 50 \cdot (-0,6427) \nonumber \\ &= 38,302 - \mathrm {j} 32,1393 \nonumber \end {align}
\(\underline {K}_2 - \underline {K}_2\) in kartesischen Koordinaten subtrahieren:
\begin {align} \underline {K}_1 - \underline {K}_2 &= (10 + \mathrm {j} \cdot 40) - (38,302 - \mathrm {j} 32,1393) \nonumber \\ &= 10 + \mathrm {j} \cdot 40 - 38,302 + \mathrm {j} 32,1393 \nonumber \\ &= -28,3 + \mathrm {j} 72,139 \nonumber \end {align}
Ergebnis in Polarkoordinaten:
\begin {align} \underline {K}_1 - \underline {K}_2 &= \sqrt {\Re ^2+\Im ^2} \cdot \mathrm {e}^{\mathrm {j}\arctan (\frac {\Im }{\Re })} \nonumber \\ &= 77,49 \cdot \mathrm {e}^{\mathrm {j}111,42^\circ } \nonumber \end {align}
-
\(K_3 + K_2\), Ergebnis in kartesischen Koordinaten
\begin {align} K_3 &= 250 \cdot e^{j\frac {\pi }{4}} = 176,78 + j176,78 \nonumber \\ K_2 &= 50 \cdot e^{-j40^\circ } = 38,3 - j32,15 \nonumber \\ K_3 + K_2 &= (176,78 + j176,78) + (38,3 - j32,15) \nonumber \\ K_3 + K_2 &= 215,08 + j144,63 \nonumber \end {align}
-
\(K_1 \cdot K_3\), Ergebnis in Polarkoordinaten
\begin {align} \underline {K}_1 &= 10 + \mathrm {j}40 \nonumber \\ &= 41,23 \cdot \mathrm {e}^{\mathrm {j}75,96^\circ } \nonumber \\ \underline {K}_1 \cdot \underline {K}_3 &= 10 + \mathrm {j}40 \cdot 250 \cdot \mathrm {e}^{\mathrm {j}45^\circ } \nonumber \\ &= 10307,75 \cdot \mathrm {e}^{\mathrm {j}120,96^\circ } \nonumber \end {align}
-
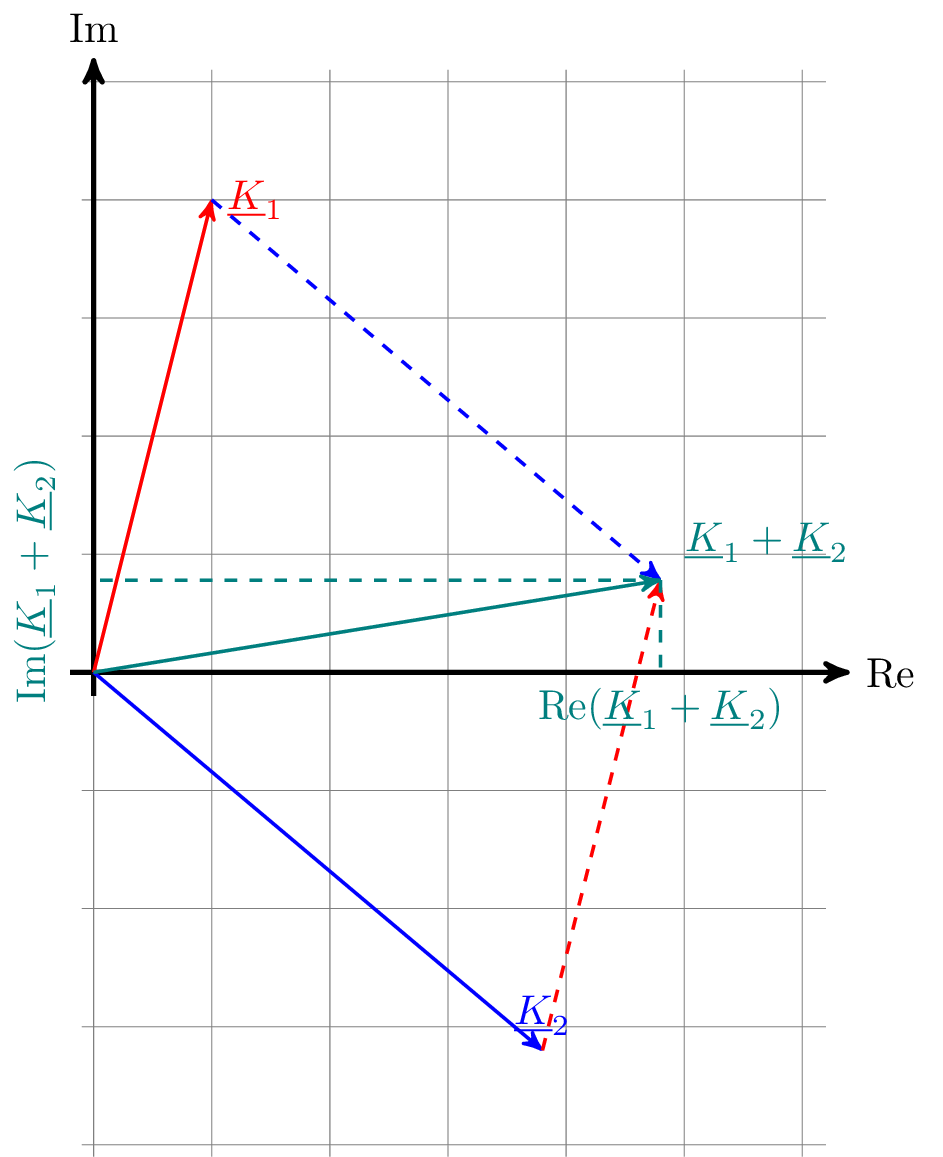
\(K_1 + K_2\), zeichnerisch im Zeigerdiagramm
![Das Bild zeigt ein komplexes Zeigerdiagramm mit Real- und Imaginärachse. Zwei komplexe Zahlen werden vektoriell addiert, wobei Hilfslinien die Real- und Imaginärteile der Summe markieren. Der resultierende Zeiger stellt die Summe der beiden komplexen Zahlen dar. Die Darstellung veranschaulicht die geometrische Addition im komplexen Zahlenraum.]()
-
\((K_1 - K_2)^2\)
Ergebnis aus Teil a): \begin {align} K_1 - Z_2 = 77,49 \cdot \mathrm {e}^{\mathrm {j}111,42^\circ } \nonumber \end {align}
Regel für das Quadrat einer komplexen Zahl: \begin {align} (K_1 - K_2)^2 &= 77,49^2 \cdot \mathrm {e}^{\mathrm {j}2 \cdot 111,42^\circ } \nonumber \\ &= 6004 \cdot \mathrm {e}^{-\mathrm {j}137^\circ } \nonumber \end {align}
-
\(\sqrt {K_1 + K_3}\)
\begin {align} K_1 + K_3 = 186,78 + j216,78 \nonumber \end {align}
Umwandlung in Polarform:
\begin {align} K_1 + K_3 = 286,09 \cdot \mathrm {e}^{\mathrm {j}49,32^\circ } \nonumber \end {align}
Die Quadratwurzel einer komplexen Zahl in Polarform ergibt:
\begin {align} \sqrt {r \cdot \mathrm {e}^{\mathrm {j}\varphi }} &= \sqrt {r} \frac {\varphi }{2} \nonumber \\ \sqrt {286,09} \cdot \mathrm {e}^{\mathrm {j}\frac {49,32^\circ }{2}} &= 16,91 \cdot \mathrm {e}^{\mathrm {j}24,66^\circ } \nonumber \end {align}
3 Zeigerdiagramme 1
Gegeben sei die Spannung \(\hat {U} = 325\ V \cdot \mathrm {e}^{\mathrm {j}30^\circ }\).
- Zeichnen Sie das Zeigerdiagramm für die Spannung \(\hat {U}\) im komplexen Zahlenraum.
- Berechnen Sie die Real- und Imaginärteile der komplexen Spannung \(\hat {U}\).
- Erklären Sie die Bedeutung des Phasenwinkels in Bezug auf die Wechselspannung.
3.1 Lösung:
-
Zeigerdiagramm für die Spannung \(\hat {U}\)
![Das Bild zeigt ein komplexes Koordinatensystem mit Realachse (Re) und Imaginärachse (Im). Vom Ursprung aus ist ein Spannungszeiger Û eingezeichnet, der einen Winkel von 30 Grad zur positiven Realachse bildet. Der Nullwinkel 0° ist entlang der Realachse markiert.]()
-
Die Real- und Imaginärteile der Spannung \(\hat {U}\) können mit den folgenden Formeln berechnet werden:
\begin {align} U_{\text {Re}} &= \hat {U} \cdot \cos (\varphi ) = 325 \cdot \cos (30^\circ ) \approx 281,46\ V \nonumber \\ U_{\text {Im}} &= \hat {U} \cdot \sin (\varphi ) = 325 \cdot \sin (30^\circ ) = 162,5\ V \nonumber \end {align}
- Der Phasenwinkel \(\varphi \) beschreibt den zeitlichen Versatz zwischen der Spannung und dem Strom in einem Wechselstromkreis. Ein positiver Phasenwinkel deutet darauf hin, dass die Spannung der Strom nachfolgt (induktive Last), während ein negativer Phasenwinkel anzeigt, dass der Strom der Spannung nachfolgt (kapazitive Last).
4 Komplexe Wechselstromrechnung 1
Gegeben sind die spezifischen Werte für den Widerstand \(R\), die Spule \(L\) und den Kondensator \(C\).
\(R=10\ \Omega \), \(L=10\ mH\), \(C=10\ pF\)
Berechnet werden sollen die Impedanzen der drei Bauteile bei den Frequenzen:
\(1\ \mu Hz\),\(1\ mHz\),\(1\ Hz\),\(1\ kHz\),\(1\ MHz\)
Tragen Sie die Ergebnisse in eine Tabelle ein.
4.1 Lösung:
-
\(\bf Frequenz\) \(\bf X_R\) \(\bf X_C\) \(\bf X_L\) \(1\ \mu Hz\) \(10\ \Omega \) \(-j 15,92\ M\Omega \) \(j 6,28\) \(1\ mHz\) \(10\ \Omega \) \(-j 15,92\ k\Omega \) k \(1\ Hz\) \(10\ \Omega \) \(-j 15,92\ \Omega \) k \(1\ kHz\) \(10\ \Omega \) \(-j 15,92\ m\Omega \) \(1\ MHz\) \(10\ \Omega \) \(-j 15,92\ \mu \Omega \)
5 Komplexe Wechselstromrechnung 2
Eine Impedanz weist bei der Frequenz \(f = 1\ kHz\) den Wert \(\underline {Z} = (300+\mathrm {j}400)\ \Omega \) auf.
- Bestimmen Sie den Scheinwiderstand (Betrag) der Impedanz.
- Ermitteln Sie die Admittanz \(\underline {Y} = \frac {1}{\underline {Z}}\) sowie den Scheinleitwert.
- Geben Sie zur Realisierung der Impedanz \(\underline {Z}\) eine Schaltung aus zwei in Reihe geschalteten Bauelementen an und dimensionieren Sie diese Schaltung.
- Geben Sie zur Realisierung der Impedanz \(\underline {Z}\) eine Schaltung aus zwei parallel geschalteten Bauelementen an und dimensionieren Sie diese Schaltung.
Außerdem wird an die Impedanz \(\underline {Z} = (300+\mathrm {j}400)\ \Omega \) eine Spannung \(u(t)=\hat {U} \cdot \cos (2\pi f t + \varphi _U)\) mit \(\hat {U}=5\ V\), \(\varphi _U=\pi /4\) und \(f=1\ kHz\) gelegt.
- Ermitteln Sie die komplexe Amplitude \(\underline {\hat {U}}\) der anliegenden Spannung.
- Berechnen Sie die komplexe Amplitude \(\underline {\hat {I}}\) des Stromes durch die Impedanz.
5.1 Lösung:
- \begin {align} |\underline {Z}| &= \sqrt {Re^2+Im^2} \nonumber \\ &= \sqrt {300^2+400^2}\ \Omega \nonumber \\ &= 500\ \Omega \nonumber \end {align}
- \begin {align} \underline {Y} &= \frac {1}{\underline {Z}} = \frac {1}{(300+\mathrm {j}400)\ \Omega } \nonumber \\ &= \frac {1}{(300+\mathrm {j}400)\ \Omega } \cdot \frac {(300-\mathrm {j}400)\ \cancel {\Omega }}{(300-\mathrm {j}400)\ \cancel {\Omega }} \nonumber \\ &= \frac {1}{300^2+400^2} \cdot (300-\mathrm {j}400)\ S \nonumber \\ &= (0.0012-\mathrm {j}0.0016)\ S \nonumber \\ |\underline {Y}| &= \frac {1}{|\underline {Z}|} \nonumber \\ &= \frac {1}{500}\ S \nonumber \end {align}
-
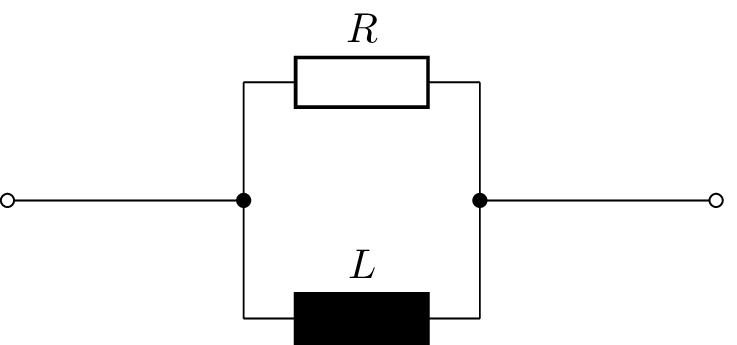
Reihenschaltung:
Realteil \(\rightarrow \) Ohmscher Wiederstand
Imaginärteil \(\rightarrow \) Spule oder Kondensator?
Reaktanz Spule: \(X_L=2\pi f \cdot L > 0\)
Reaktanz Kondensator: \(X_C=-\frac {1}{2\pi f\cdot C} < 0\)
![Das Bild zeigt eine Reihenschaltung aus einem Widerstand R und einer Spule L. Beide Bauteile sind durch eine Leitung verbunden und besitzen jeweils einen Anschluss links und rechts. Die Darstellung veranschaulicht eine einfache RL-Reihenschaltung.]()
\begin {align} R &= 300\ \Omega \nonumber \\ L &= \frac {X_L}{2\pi \cdot f} \nonumber \\ &= \frac {400\ \Omega }{2\pi \cdot 1\ kHz} \nonumber \\ &= 63.66\ mH \nonumber \\ \underline {Z} &= R+\mathrm {j}X_L = R+\mathrm {j}\ 2\pi \cdot f \cdot L \nonumber \end {align}
-
Parallelschaltung:
\(\rightarrow \) Addition von Leitwerten:
\begin {equation} \underline {Y} = G + \mathrm {j}B = (0.0012-\mathrm {j}0.0016)\ S \qquad (\text {aus b)}) \nonumber \end {equation}
\(B<0 \rightarrow \) Spule, induktiver Blindleitwert
\(B>0 \rightarrow \) Kondensator, kapazitiver Blindleitwert
![Das Bild zeigt eine Parallelschaltung aus einem Widerstand R und einer Spule L. Beide Bauteile sind zwischen denselben zwei Knoten angeschlossen. Die Darstellung veranschaulicht eine RL-Parallelschaltung.]()
\begin {align} R &= \frac {1}{G} \nonumber \\ &= \frac {1}{0.0012\ S} \nonumber \\ &= 833\ \Omega \nonumber \\ B &= -\frac {1}{2\pi \cdot f \cdot L} \nonumber \\ L &= \frac {1}{2\pi \cdot f \cdot B} \nonumber \\ &= 99.47\ mH \nonumber \end {align}
- \begin {align} \underline {U} &= \hat {U} \cdot \mathrm {e}^{\mathrm {j} \varphi _\mathrm {U}} = 5\ V \cdot \mathrm {e}^{\mathrm {j} \pi /4} = 5\ V \cdot \mathrm {e}^{\mathrm {j} 45^\circ } \nonumber \\ &= 5\ V \cdot (\cos (45^\circ )+\mathrm {j}\sin (45^\circ )) \nonumber \\ &= 5\ V \cdot \frac {\sqrt {2}}{2} (1+\mathrm {j}) \nonumber \\ &\approx (3,53 + \mathrm {j} 3,53) \ V \nonumber \end {align}
6 Effektivwert 1
Gegeben sei eine sinusförmige Spannung
\begin {equation} u(t) = 150\ V \cdot \sin (100\pi t) \nonumber \end {equation}
wobei \(t\) in Sekunden und die Spannung \(u(t)\) in Volt angegeben sind.
Berechnen Sie für diese Spannung:
- Den arithmetischen Mittelwert \(\bar {u}\) der Spannung über eine Periode.
- Den Effektivwert \(U_{Eff}\) der Spannung.
6.1 Lösung:
-
Der arithmetische Mittelwert einer Funktion u(t) über eine Periode T ist gegeben durch: \begin {equation} \bar {u} = \frac {1}{T} \int _0^T u(t) dt \nonumber \end {equation}
Da \(u(t)\) eine Sinusfunktion darstellt und die Sinuswelle über eine Periode symmetrisch ist, heben sich die positiven und negativen Teile der Welle gegenseitig auf. Daher ist der arithmetische Mittelwert für jede Sinuswelle immer null:
-
Der Effektivwert einer Sinusspannung \(u(t)\) wird durch die folgende Formel berechnet: \begin {equation} U_{Eff} = \frac {\hat {U}}{\sqrt {2}} \nonumber \end {equation}
In diesem Fall ist \(\hat {U} = 150\ V\), die Amplitude der Spannung.
\begin {equation} U_{Eff} = \frac {150\ V}{\sqrt {2}} \approx \frac {150\ V}{1.414} \approx 106.1\ V \nonumber \end {equation}
7 Leistungsberechnung 1
Gegeben ist in in blau das zeitabhändige Spannungssignal und in rot das zeitabhängige Stromsignal.
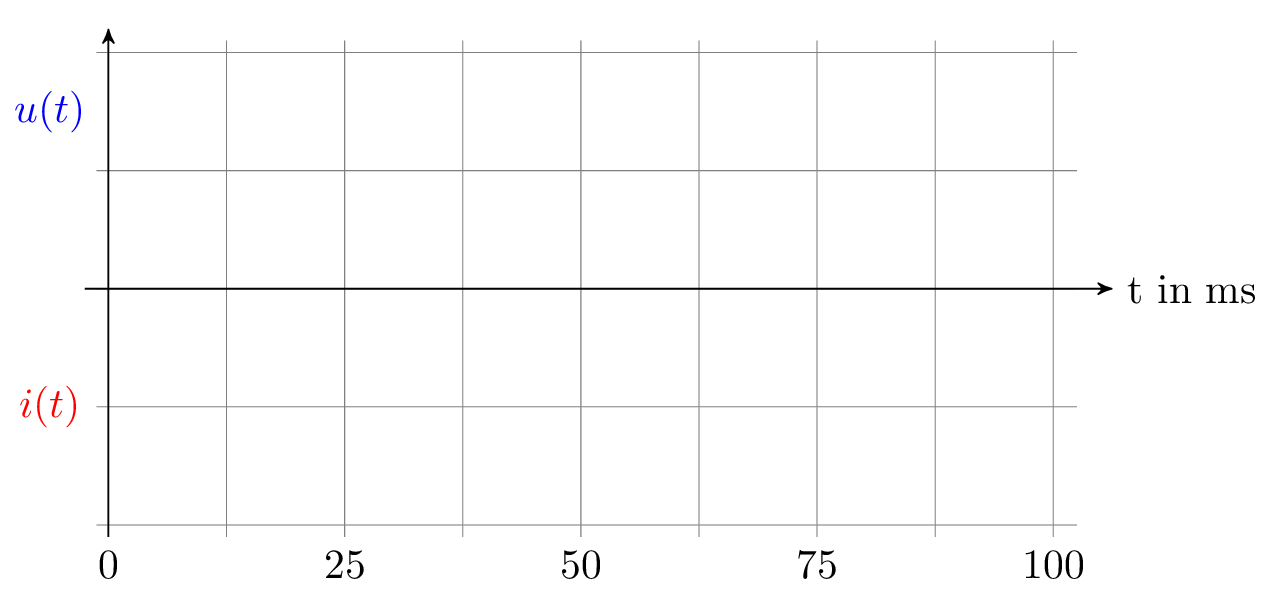
Hierzu sollen die folgenden Aufgaben bearbeitet werden:
- Ablesen des Betrages der Phasenwinkel von Spannung und Strom. Bennenung des Verhaltens.
- Angabe von Periodendauer, Frequenz und Kreisfrequenz.
- Berechnung der Augenblicksleistung zum Zeitpunkt t = 12,5 ms.
- Berechnung von Wirkleistung und Blindleistung.
- Berechnung der Scheinleistung mit dem konjugierten komplexen Strom.
7.1 Lösung:
- Die Spannung weist einen Phasenwinkel von \(\varphi _\mathrm {u}=0\) und der Strom weist einen Phasenwinkel von \(\varphi _\mathrm {i}=\pi /3\) auf.
Das Nacheilen des Stromes deutet auf ein induktives Verhalten hin. - Die Periodendauer T beträgt \(50\ ms\).
Die Frequenz beträgt: \begin {equation} f=\frac {1}{T}=\frac {1}{50\ ms}= 20\ Hz \nonumber \end {equation} Die Kreisfrequenz beträgt: \begin {equation} \omega = 2\pi \cdot f = 2\pi \cdot 20\ Hz = 125,66\ Hz \nonumber \end {equation} - Die Augenblicksleistung zum Zeitpunkt t = 12,5 ms beträgt: \begin {align} p(t) &= u(t) \cdot i(t) = 12\ V \cdot \sin (2\pi \cdot 20\ Hz\cdot 0,0125\ s) \cdot 2\ A \cdot \sin (2\pi \cdot 20\ Hz\cdot 0,0125\ s+\frac {\pi }{3}) \nonumber \\ p(t) &= 12\ W \nonumber \end {align}
- Die Wirkleistung beträgt: \begin {align} P &= U \cdot I \cdot \cos (\varphi ) = \frac {\hat {U}}{\sqrt {2}} \cdot \frac {\hat {I}}{\sqrt {2}} \cdot \cos (\varphi ) = \frac {12\ V}{\sqrt {2}} \cdot \frac {2\ A}{\sqrt {2}} \cdot \cos (60^o) \nonumber \\ P &= 6\ W \nonumber \end {align} Die Blindleistung beträgt: \begin {align} Q &= U \cdot I \cdot \sin (\varphi ) = \frac {\hat {U}}{\sqrt {2}} \cdot \frac {\hat {I}}{\sqrt {2}} \cdot \sin (\varphi ) = \frac {12\ V}{\sqrt {2}} \cdot \frac {2\ A}{\sqrt {2}} \cdot \sin (60^o) \nonumber \\ Q &= 10,392\ var \nonumber \end {align}
- Die Scheinleistung beträgt: \begin {align} \underline {S} &= \underline {U} \cdot \underline {I}^* = \frac {\underline {\hat {U}}}{\sqrt {2}} \cdot \frac {\underline {\hat {I}}^*}{\sqrt {2}} = \frac {12\ V}{\sqrt {2}} \cdot e^{j(2\pi \cdot 20\ Hz)} \cdot \frac {2\ A}{\sqrt {2}} \cdot e^{j(2\pi \cdot 20\ Hz+\frac {\pi }{3})} \nonumber \\ \underline {S} &= 12\ VA \cdot e^{j\frac {\pi }{3}} = 6\ W + j10,392\ var \nonumber \end {align}
8 Drehstrom 1
Ein Drehstrommotor hat die folgenden Nennwerte:
- Nennspannung \(U_N = 400\ V\)
- Nennstrom \(I_N = 10\ A\)
- Berechnen Sie die Spannung über jede Wicklung des Motors im Sternbetrieb \(U_Y \).
- Berechnen Sie die Spannung über jede Wicklung des Motors im Dreieckbetrieb \(U_\Delta \).
- Berechnen Sie den Strom durch jede Wicklung \(I_Y \) im Sternbetrieb.
- Berechnen Sie den Strom durch jede Wicklung \(I_\Delta \) im Dreieckbetrieb.
8.1 Lösung:
- Spannung über jede Wicklung des Motors \(U_Y \) im Sternbetrieb: \begin {align} U_Y = \frac {U_N}{\sqrt {3}} = \frac {400\ V}{\sqrt {3}} \approx 230.94\ V \nonumber \end {align}
- Spannung über jede Wicklung des Motors \(U_\Delta \) im Dreieckbetrieb: \begin {align} U_\Delta = U_N = 400\ V \nonumber \end {align}
- Strom durch jede Wicklung \(I_Y \) im Sternbetrieb: \begin {align} I_Y = I_N = 10\ A \nonumber \end {align}
- Strom durch jede Wicklung \(I_\Delta \) im Dreieckbetrieb: \begin {align} I_\Delta = \sqrt {3} \cdot I_Y = \sqrt {3} \cdot 10\ A \approx 17.32\ A \nonumber \end {align}
9 Drehstrom 2
Es ist ein symmetrisches Drehstromsystem mit folgenden Spannungen gegeben:
\(\underline {U}_1=230~V\), \(\underline {U}_2=230~V\cdot \underline {a}^2\), \(\underline {U}_3=230~V\cdot \underline {a}\)
Die Impedanzen haben alle den Wert \(Z=10\Omega \)
Für alle Aufgabenteile gilt: Lösen Sie die Aufgaben mit dem geringstmöglichen Aufwand!
- Zeichnen Sie die dreiphasigen und einphasigen ESB in Stern- und Dreieckschaltung und beschrifften Sie die ESB korrekt!
- Berechnen Sie den Betrag der Verbraucherspannungen sowohl für die Stern- als auch die Dreieckschaltung!
- Berechnen Sie die komplexen Verbraucherspannungen in der Dreieckschaltung!
- Zeichnen Sie die Zeigerdiagramme der Verbaucherspannungen für die Stern- und Dreieckschaltung!
- Berechnen Sie die komplexen Lastströme für die Sternschaltung und den Betrag der Lastströme für die Dreieckschaltung!
- Berechnen Sie die Scheinleistung für die Stern- und Dreieckschaltung!
9.1 Lösung:
-
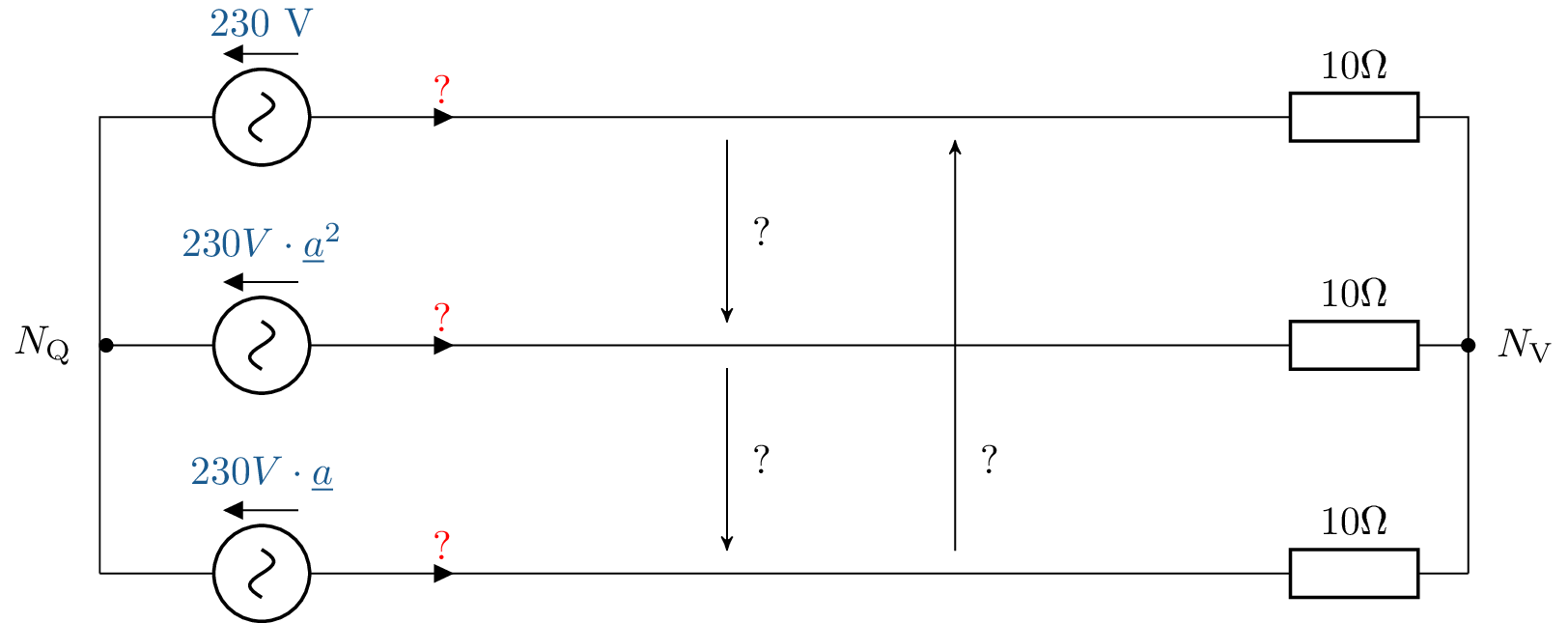
ESBs der Sternschaltung:
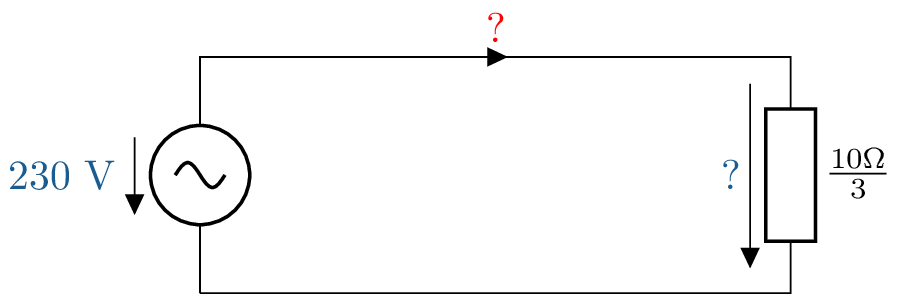
![Das Bild zeigt ein Schaltbild zur Analyse einer Drehstromschaltung mit 230-Volt-Quellen. Es ist eine Sternschaltung mit Impedanzen von 10 Ohm und unbekannten Strömen und Spannungen dargestellt.]()
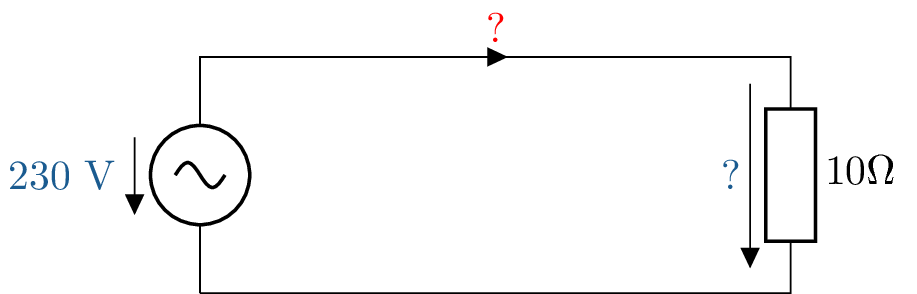
![Das Bild zeigt ein Schaltbild zur Analyse einer Drehstromschaltung mit 230-Volt-Quellen. Es
wird das vereinfachte Ersatzschaltbild eines einzelnen Strangs gezeigt.]()
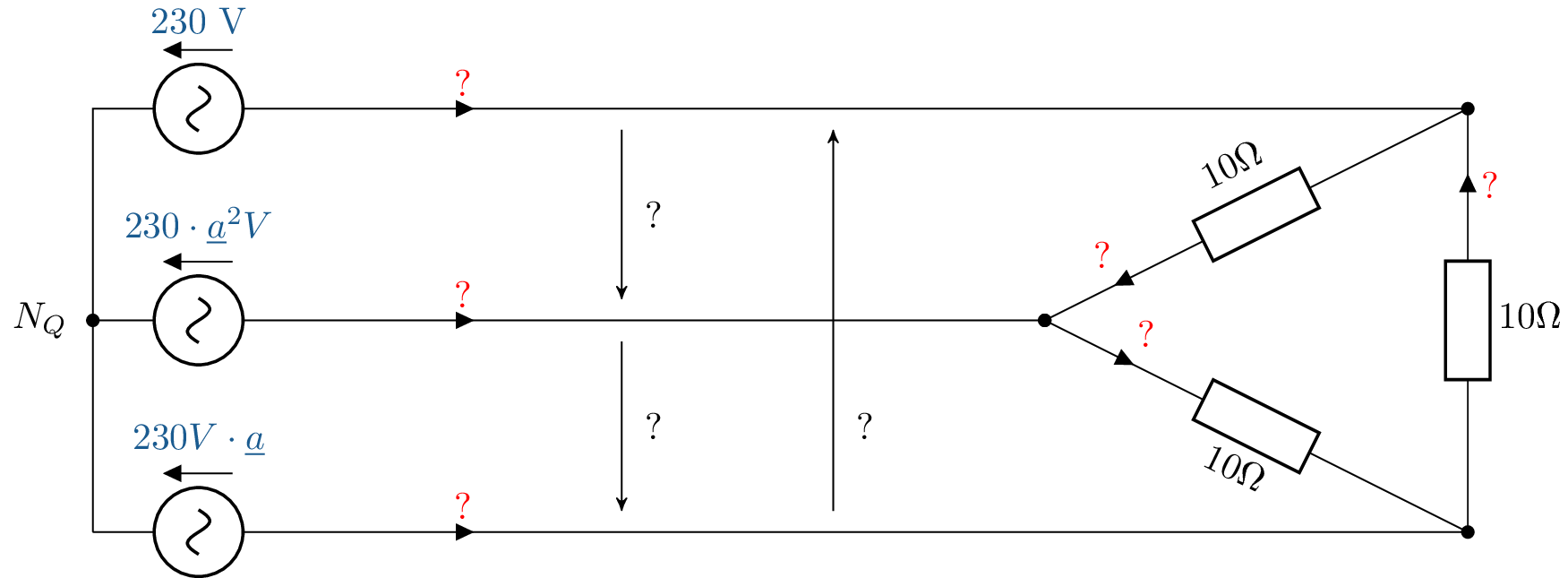
ESBs der Dreieckschaltung:
![Das Bild zeigt ein Schaltbild zur Analyse einer Drehstromschaltung mit 230-Volt-Quellen. Es ist eine Dreieckschaltung mit Impedanzen von 10 Ohm und unbekannten Strömen und Spannungen dargestellt.]()
![Das Bild zeigt ein Schaltbild zur Analyse einer Drehstromschaltung mit 230-Volt-Quellen.
Es wird das vereinfachte Ersatzschaltbild eines einzelnen Strangs gezeigt, wobei die
Lastimpedanzen angepasst dargestellt sind.]()
- Der Betrag Verbraucherspannungen ist in der Sternschaltung gleich der Quellspannung: 230 V
Der Betrag Verbraucherspannungen ist in der Dreieckschaltung \(\sqrt {3}\) mal größer als in der Sternschaltung: \(230 V\cdot \sqrt {3}=398,37 V\approx 400 V\) -
Die komplexe Verbaucherspannungen in der Dreieckschaltung errechnet sich aus den Differenzen der Sternspannungen.
\begin {align} \underline {U}_\mathrm {L1L2}&=\underline {U}_\mathrm {L1}-\underline {U}_\mathrm {L2}=230 V-230 V\cdot \underline {a}^2 \notag \\ &=230 V(1-(-\frac {1}{2}-j\frac {\sqrt {3}}{2}))=\sqrt {3}\cdot 230 V(\frac {3}{2}+j\frac {1}{2}) \notag \\ &=\sqrt {3}\cdot 230 V\cdot e^{j\cdot 30^\circ } \notag \end {align} \begin {align} \underline {U}_\mathrm {L2L3}&=\underline {U}_\mathrm {L2}-\underline {U}_\mathrm {L3}=230 V\cdot \underline {a}^2-230 V\cdot \underline {a} \notag \\ &=230 V(-\frac {1}{2}-j\frac {\sqrt {3}}{2}-(-\frac {1}{2}+j\frac {\sqrt {3}}{2}))=\sqrt {3}\cdot 230 V(-j) \notag \\ &=\sqrt {3}\cdot 230 V\cdot e^{-j\cdot 90^\circ } \notag \end {align} \begin {align} \underline {U}_\mathrm {L3L1}&=\underline {U}_\mathrm {L3}-\underline {U}_\mathrm {L1}=230 V\cdot \underline {a}-230 V \notag \\ &=230 V(-\frac {1}{2}+j\frac {\sqrt {3}}{2}-1)=\sqrt {3}\cdot 230 V(-\frac {\sqrt {3}}{2}+j\frac {1}{2}) \notag \\ &=\sqrt {3}\cdot 230 V\cdot e^{j\cdot 150^\circ } \nonumber \end {align}
-
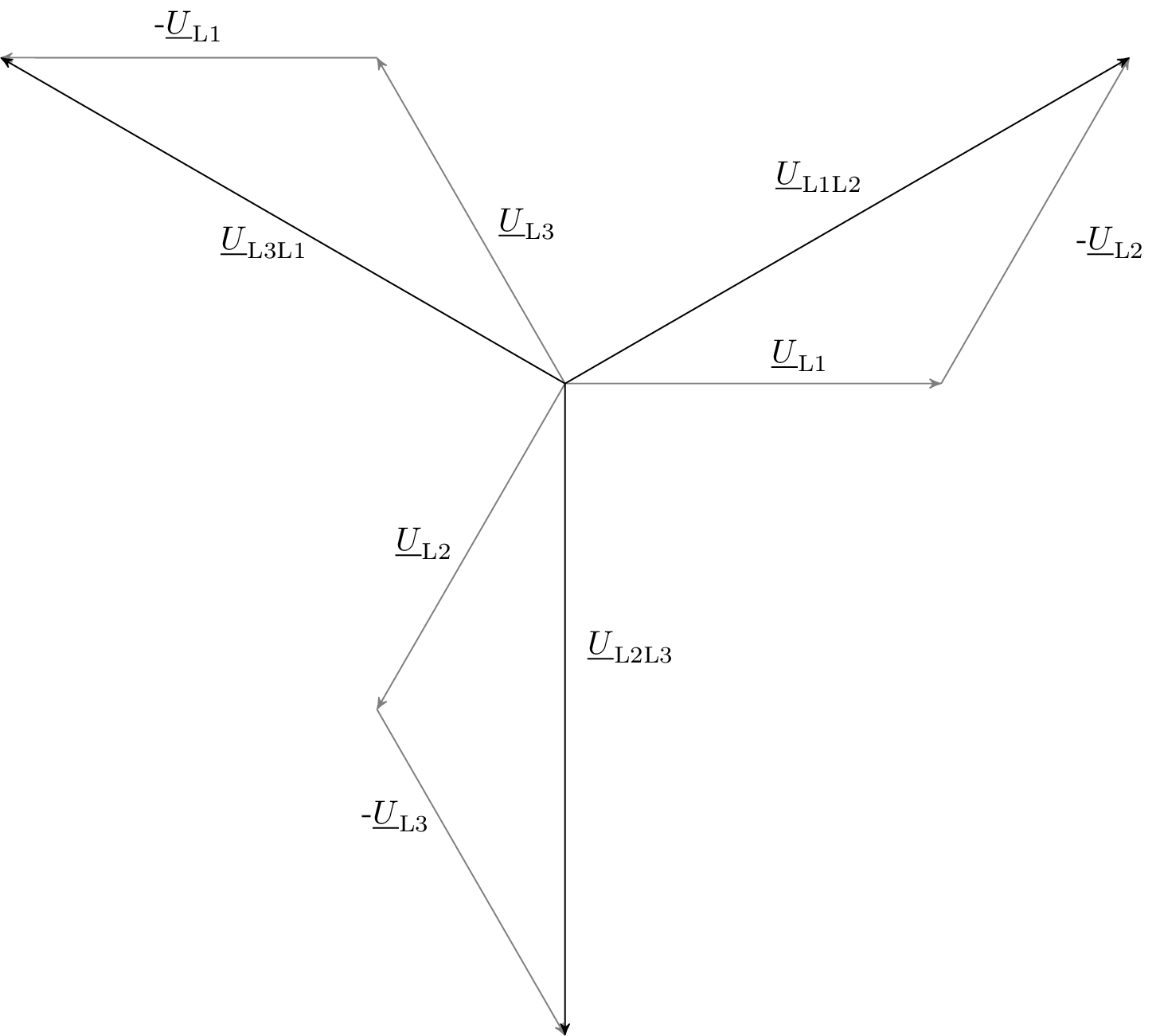
Zeigerdiagramme der Verbaucherspannungen für die Stern- und Dreieckschaltung:
![Das Bild zeigt ein Zeigerdiagramm eines Drehstromsystems mit Leiter- und Außenleiterspannungen. Von einem gemeinsamen Ursprung gehen mehrere Spannungszeiger aus, darunter U˙L1, U˙L2 und U˙L3 sowie die zugehörigen Außenleiterspannungen wie U˙L1L2, U˙L2L3 und U˙L3L1. Zusätzlich sind einige Spannungen mit umgekehrter Richtung gekennzeichnet, zum Beispiel You may provide a definition withU˙L2 und You may provide a definition withU˙L3. Die Grafik veranschaulicht die geometrischen Beziehungen der Spannungen im Drehstromnetz.]()
-
Der Strom wird über das Ohmsche Gesetz berechnet. Für die Sternschaltung gilt:
\begin {align} \underline {I}_1&=\frac {\underline {U}_\mathrm {L1}}{\underline {Z}}=\frac {230 V}{10\ohm }=23 A \notag \\ \underline {I}_2&=\frac {\underline {U}_\mathrm {L2}}{\underline {Z}}=\frac {230 V\cdot \underline {a}^2}{10\ohm }=23 A\cdot \underline {a}^2 \notag \\ \underline {I}_3&=\frac {\underline {U}_\mathrm {L3}}{\underline {Z}}=\frac {230 V\cdot \underline {a}}{10\ohm }=23 A\cdot \underline {a} \notag \end {align}
Bei dem Dreieckstrom wird zwischen dem Strangstrom und dem Dreieckstrom, also dem Strom durch die Verbraucher unterschieden. Der Strom in den Verbauchersträngen kann mit den Spannung über die Verbraucher in der Dreieckschaltung errechnet werden:
\begin {align} I_\Delta &=\frac {U\Delta }{Z}=\frac {400V}{10\ohm }=40 A \notag \end {align}
Der Strom im Strang ist wiederum um \(\sqrt {3}\) größer, als in den Verbauchersträngen: \begin {align} I_\mathrm {str}=\sqrt {3}\cdot I_\Delta =\sqrt {3}\cdot 40 A=69,28 A \notag \end {align}
Dieser Wert entspricht dem dreifachen Wert des Stroms in einer Sternschaltung
-
Die allgemein Leistungsgleichung ist folgende:
\begin {align} S=\sqrt {3}\cdot U_\Delta \cdot I_\mathrm {str} \notag \end {align}
Welcher Strom eingesetzt werden muss, hängt von der jeweiligen Schaltung ab. Wie in Aufgabe 5. berechnet ist der Strangstrom in der Dreieckschaltung um den Faktor 3 größer als in der Sternschaltung
Für die Sternschaltung gilt: \begin {align} S=\sqrt {3}\cdot U\cdot I=\sqrt {3}\cdot 400 V \cdot 23 A=15.934 VA \notag \end {align}
Und für die Dreieckschaltung gilt: \begin {align} S=\sqrt {3}\cdot U\cdot I=\sqrt {3}\cdot 400 V \cdot 3\cdot 23 A=47.804 VA \notag \end {align}
10 Mehrphasensysteme 1
Gegeben ist ein unsymmetrisches System mit folgenden Spannungen:
\(\underline {U}_\mathrm {L1}=230 V\), \(\underline {U}_\mathrm {L2}=460 V\cdot e^{-j45^\circ }\), \(\underline {U}_\mathrm {L1}=345 V\cdot e^{j120^\circ }\)
- Zeichen Sie das Zeigerdiagramm des Originalsystems!
- Stellen Sie die Zerlegungsgleichungen für die Spannungen auf!
- Berechnen Sie die Spannungen der transformierten Systeme!
- Zeichen Sie die Zeigerdiagramme der transformierten Systeme!
10.1 Lösung:
-
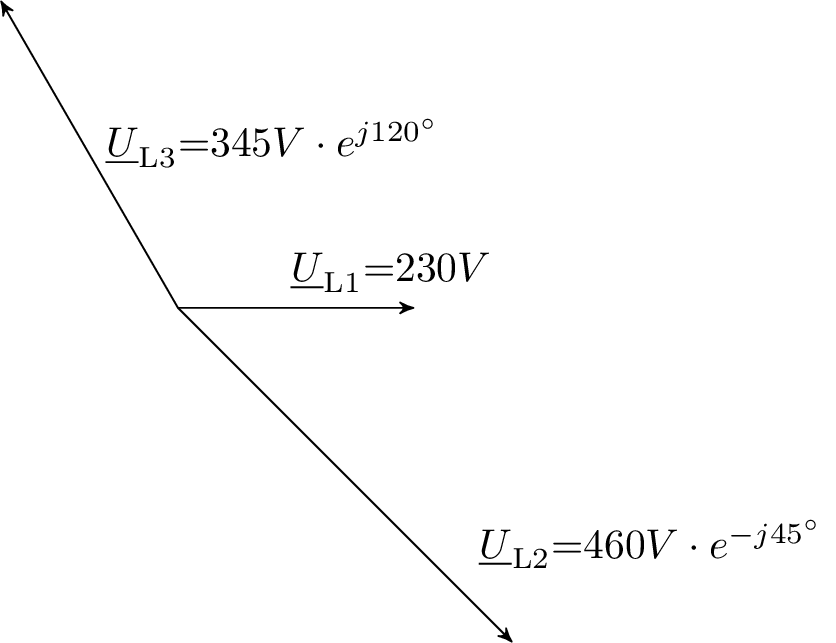
Zeigerdiagramm des Originalsystems:
![Das Bild zeigt ein Zeigerdiagramm mit drei Spannungszeigern. U˙L1 ist als waagerechter Pfeil mit 230 V eingezeichnet. U˙L3 ist ein schräg nach oben gerichteter Zeiger mit dem Betrag 345 V und der Phase +120°. U˙L2 ist ein schräg nach unten gerichteter Zeiger mit dem Betrag 460 V und der Phase You may provide a definition with45°.]()
- \begin {align} \underline {U}_{\mathrm {L1}}&=230 V=\underline {U}_{0}+\underline {U}_{1}+\underline {U}_{2} \notag \\ \underline {U}_{\mathrm {L2}}&=460 V\cdot e^{-j45^\circ }=\underline {U}_{0}+\underline {a}^2\cdot \underline {U}_{1}+\underline {a}\cdot \underline {U}_{2} \notag \\ \underline {U}_{\mathrm {L3}}&=345 V\cdot e^{j120^\circ }=\underline {U}_{0}+\underline {a}\cdot \underline {U}_{1}+\underline {a}^2\cdot \underline {U}_{2} \notag \end {align}
-
Für das Nullsystem:
\begin {align} \underline {U}_0&=\frac {1}{3}\cdot (\underline {U}_{\mathrm {L1}}+\underline {U}_{\mathrm {L2}}+\underline {U}_{\mathrm {L3}}) \notag \\ &=\frac {1}{3}\cdot (230 V+460 V\cdot e^{-j45^\circ }+345 V\cdot e^{j120^\circ }) \notag \\ &=\frac {1}{3}\cdot (230V+325,27V-j325,27V-172,5V+298,78V) \notag \\ &=127,59V-j8,83=127,9\cdot e^{-j3,56^\circ } \notag \end {align}
Für das Mitsystem:
\begin {align} \underline {U}_{1}&=\frac {1}{3}\cdot (\underline {U}_{\mathrm {L1}}+\underline {a}\cdot \underline {U}_{\mathrm {L2}}+\underline {a}^2\cdot \underline {U}_{\mathrm {L3}}) \notag \\ &=\frac {1}{3}\cdot (230V+(-\frac {1}{2}+j\frac {\sqrt {3}}{2})\cdot (325,27V-j325,7V)+(-\frac {1}{2}-j\frac {\sqrt {3}}{2})\cdot (-172,5V+298,78V)) \notag \\ &=\frac {1}{3}\cdot (230V+119,42V+j444,54V+345V) \notag \\ &=231,48V+j148,18V=274,84\cdot e^{j32,63^\circ } \notag \end {align}
Für das Gegensystem:
\begin {align} \underline {U}_{2}&=\frac {1}{3}\cdot (\underline {U}_{\mathrm {L1}}+\underline {a}^2\cdot \underline {U}_{\mathrm {L2}}+\underline {a}\cdot \underline {U}_{\mathrm {L3}}) \notag \\ &=\frac {1}{3}\cdot (230V+(-\frac {1}{2}-j\frac {\sqrt {3}}{2})\cdot (325,27V-j325,7V)+(-\frac {1}{2}+j\frac {\sqrt {3}}{2})\cdot (-172,5V+298,78V)) \notag \\ &=\frac {1}{3}\cdot (230V+(-444,33V-j119,16V)+(-172,5V-298,78V)) \notag \\ &=-128,95V-j139,28V=189,8\cdot e^{j132,79^\circ } \notag \end {align}
-
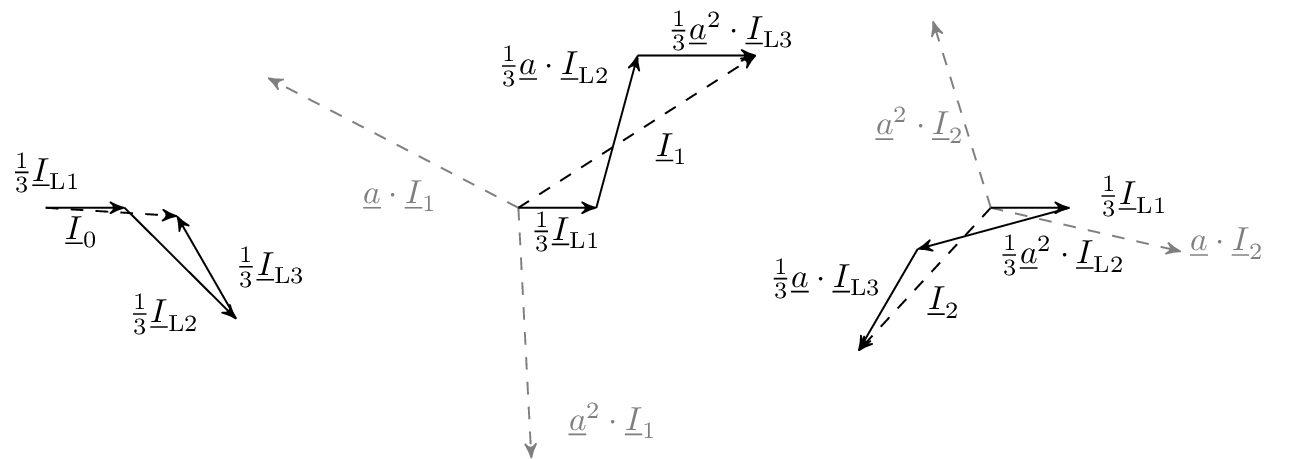
Zeigerdiagramme der transformierten Systeme:
![Das Bild zeigt mehrere Zeigerdiagramme zur Zerlegung von Leiterströmen in symmetrische Komponenten. Dargestellt sind Anteile der Ströme I˙L1, I˙L2 und I˙L3, jeweils skaliert mit dem Faktor 1/3 und phasenverschoben mit den Operatoren a und a². Gestrichelte Pfeile kennzeichnen die phasenverschobenen Komponenten. Die Grafik veranschaulicht die Bildung von Mit-, Gegen- und Nullsystemströmen.]()
Anmerkung: Das Erstellen der Zeigerdiagramme ist ein guter Weg um die errechneten Ergebnisse aus 3. zu überprüfen. Die Wege der Zeiger, die aus dem Originalsystem genommen werden, müssen da enden, wo auch der Zeiger des transformierten Systems hinführt. Stimmen die Endpunkte nicht überein, wurde in einer der Rechnungen ein Fehler gemacht.