Im Modul 12
Grundlagen der Berechnung von Schaltvorgängen
Schaltvorgänge im Zeitbereich berechnenGrundlage der Berechnung von Schaltvorgängen sind Differentialgleichungen (DGL).
Die Aufstellung der Kirchhoffschen Regeln bei Schaltungen mit Energiespeichern führt zu DGL von Spannungen an beziehungsweise Strömen in den jeweiligen Komponenten. Das bedeutet, dass die jeweiligen Momentanwerte von Spannungen und Strömen nicht ausreichen, um den Zustand des Systems zu beschreiben.
Die Zeitverläufe von Spannungen und Strömen während Schaltvorgängen lassen sich durch Lösung ihrer jeweiligen DGL bestimmen.
Lernziele: Grundlagen
Studierende lernen:
Tabelle 1 zeigt eine Übersicht wichtiger Begriffe mit Kurzform der hier verwendeten Definitionen. Bestimmte Begriffe werden in den folgenden Abschnitten genauer erläutert und diskutiert.
Speziell die hier verwendeten Definitionen für Transienten, Ausgleichs-, Einschwing- und Schaltvorgänge werden in Abschnitt 1.2 in Abgrenzung zur Definition in anderen Quellen erläutert und die Wahl der hier getroffenen Definition begründet.
Die Tabelle dient als Referenz für die Verwendung der Begriffe in diesem Modul und kann nach Art eines Glossars verwendet werden.
| G. | Begriffe | Definitionen |
|
allg. | Schalten | „durch Betätigen eines Schalters in einen (Betriebs)zustand versetzen“[?] |
| Schalter | Komponente, hier zum öffnen oder schließen einer elektr. Verbindung | |
|
Eigenschaften | harmonisch\(^1\) | sinusförmig, beschreibt Schwingung der Form: \(y(t) = \hat {X} \cdot \sin (\omega t + \varphi )\) |
| periodisch\(^1\) | „in gleichen Abständen, regelmäßig [auftretend, wiederkehrend]“[?] | |
| zeitinvariant\(^1\) | invariant/unveränderlich über die Zeit | |
| gewöhnlich\(^2\) | Ableitung(en) nach einer unabhängigen Variable (z.B. Zeit \(t\)), Vgl. partiell | |
| homogen\(^2\) | Form gewöhnlich: \(\sum a_i(t) \frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\, f_i(y(t)) \overset {!}{=} 0\) mit Störfunktion \(b=0\) \(\vphantom {\Big |}\) | |
| linear\(^2\) | Form gewöhnlich: \(\sum a_i(t) \frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\, y(t) = b(t)\) d.h. mit \(\frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\, y(t)\) linear \(\vphantom {\Big |}\) | |
| Ordnung\(^2\) | \(n\) \([1]\) d.h. höchstens Ableitung der Ordnung \(n\) in DGL | |
|
Größen | Abklingkonst. | \(\mathrm{d}elta \) \([\mathrm {s}^{-1}]\) Maß für die Dämpfung linear gedämpfter Schwingungssysteme |
| Dämpfungskonst. | \(\mathrm{d}elta \) \([\mathrm {s}^{-1}]\) synonym zu Abklingkonstante | |
| Eigenfreq. | \(f_{0/d}\) \([\mathrm {Hz}]\) Freq. mit der ein System (un/)gedämpft selbst schwingen kann | |
| Resonanzfreq. | \(f_0\) \([\mathrm {Hz}]\) Freq. bei der ein System in Resonanz tritt, gleich unged. Eigenfreq. | |
| Zeitkonstante | \(\tau \) \([\mathrm {s}]\) Maß für Steilheit von Exponentialverläufen der Form \(\mathrm {e}^{-1/{t}{\tau }}\) | |
|
Vorgänge | Ausgleichsvorg. | Vorgang in einem System, dass einen stationären Zustand anstrebt |
| Ausschwingvorg. | Ausgleichsvorgang, schwingend, exergon (spontan) | |
| Einschwingvorg. | Ausgleichsvorgang, schwingend, endergon (nicht spontan) | |
| Schaltvorg. | nicht stationärer Zustand nach Schalten | |
| Transiente | Ausgleichsvorgang (synonym), Vgl. transient (adj.) | |
|
Zustände | eingeschwungen | stationär nach Einschwingvorgang |
| persistent | stationär von Lat. persistere, Dt. verharren, Ggt. von transient | |
| stationär | zeitlich konstante/periodische Größen (z.B. bei DC/AC) [?, S. 362] | |
| transient | übergangsweise von Lat. transire, Dt. (hin)übergehen, Ggt. von persistent | |
| \(^1\)allgemein \(^2\)bezogen auf DGL |
ZUSTÄNDE:
ausgeglichen: Beschreibt einen stationären Zustand nach einem Ausgleichsvorgang.
eingeschwungen: Beschreibt einen statiönären Zustand direkt nach einem Einschwingvorgang. Der Begriff wird in der Regel auch für stationäre Zustände nach Ausgleichsvorgängen verwendet, bei denen keine Schwingung auftritt, und zudem unabhängig von der Energieflussrichtung.
stationär: Zustandsbeschreibung für zeitlich konstante Größen (z.B. bei Gleichspannungsversorgung) oder zeitlich periodische Größen (z.B. bei Wechselspannungspannungs) [?, S. 362]
GRÖSSEN:
Die Größen Abklingkonstante, Dämpfungskonstante, Eigenfrequenz, Resonanzfrequenz und Zeitkonstante sind wichtige Kenngrößen für die Beschreibung des Schwingverhaltens von Systemen. Sie sind in Kapitel ?? am Beispiel eines RLC-Reihenschwingkreises genauer erläutert.
FÄLLE:
Die Fallunterscheidung von aperiodischem Fall, aperiodischem Grenzfall, periodischem Fall bei linearen, zeitinvarainten, schwingungsfähigen Systemen ist in Kapitel ?? am Beispiel eines RLC-Reihenschwingkreises erläutert.
Dieser Abschnitt ist für das Verständnis der Modulinhalte nicht zwingend erforderlich und als Ergänzung zu verstehen. Da einige der in Tabelle 1 aufgeführten Begriffe in der Literatur unterschiedlich verwendet werden, ist die Wahl der Definitionen hier begründet und abgegrenzt.
Verlinkung deutsch- und englischsprachiger Wikipediaartikel [Stand 15.11.2024]:
VORGÄNGE:
Ausgleichsvorgang, m.
Wie Hagmann, nur dass quasi „unterbrochene“ Ausgleichsvorgänge ebenfalls als Ausgleichsvorgänge bezeichnet werden. Diese Definition schließt Anwendungsfälle in der Leistungselektronik wie bei Hoch- und Tiefsetzstellern unter der Annahme von realen Bauteilen (\(R>0\)) mit ein.
Schaltvorgang, m.
In diesem Modul bezieht sich der Begriff Schaltvorgang nur den Vorgang nach(!) dem Schalten, welche durch dieses ausgelöst werden. Mit der hier verwendeten Definition lassen sich vom Schalten unabhängige Ausgleichsvorgänge ausschließen.
Ausschwingvorgang, m.
Bezeichnet hier exergone Ausgleichsvorgänge, das heißt Ausgleichsvorgänge, die sich bei positiver Netto-Energieabfuhr vollziehen. Entsprechend Wortbedeutung im wörtlichen Sinn, ist ein Ausschwingvorgang das Gegenstück zum Einschwingvorgang.
Einschwingvorgang, m.
Bezeichnet hier im engeren Sinn endergone Ausgleichsvorgänge, das heißt Ausgleichsvorgänge, die sich bei positiver Netto-Energiezufuhr vollziehen. Wird üblicherweise wie hier im weiteren Sinn synonym für alle Ausgleichsvorgänge verwendet. Bezieht sich hier wie üblich sowohl auf Abläufe, die schwingend als auch nicht schwingend verlaufen. [Vgl. der Worte schwingen, Schwung] Die Definition ist gewählt, um eine feinere Klassifizierung möglicher Ausgleichsvorgänge zu erleichtern.
Transiente, w.
Hier synonym zu Ausgleichsvorgang betrachtet, frei übersetzbar mit „Übergang“aus dem Lateinischen. Vergleich transient (adj.) von Lat. transire Dt. (hin-)über(/durch)-gehen, Gegenteil von persistent (adj.) von Lat. persistere Dt. verharren.
Zur Berechnung von Schaltvorgängen stehen prinzipiell zwei Methoden zur Verfügung. Beide Methoden basieren auf der Lösung der Differentialgleichung (DGL) einer Schaltung.
Die Lösung der DGL erfolgt:
Abbildung 1 stellt den Ablauf zur Berechnung im Zeit- und im Bildbereich zum Vergleich als Flussdiagramm gegenüber.
Die Benennung und Darstellung beider Methoden sind angelehnt an [?, S. 51], finden sich jedoch in ähnlicher Form auch in anderen Lehrbüchern zur Elektrotechnik, Regelungstechnik und Systemtheorie.
Die Lösung der DGL im Zeitbereich ist die allgemein anwendbare Methode und wird in diesem Modul ausführlich behandelt. Der Rechenaufwand kann je nach Komplexität der DGL stark variieren. Die Methode basiert auf der Zerlegung in einen flüchtigen und einen eingeschwungenen Zustand.
Die Lösung der DGL im Bildbereich mithilfe der Laplace-Transformation ist eine spezielle Methode, die bei linearen, zeitinvarianten Systemen mit Energiespeichern angewendet werden kann. Sie bietet sich bei verschwindenden Anfangsbedingungen (Vgl. Kapitel 4) an. In einigen Fällen kann die Methoden den Rechenaufwand reduzieren, da die transformierte DGL algebraisch gelöst werden kann. Die Methode wird in diesem Modul nicht weiter behandelt.
Die Idee in den Bildbereich zu wechseln findet sich wieder in Abschnitt 3 bei der Aufstellung einer DGL und in Abschnitt 4.3 bei der Anwendung komplexer Wechselstromrechnung (Vgl. Modul 7) zur Bestimmung eingeschwungener Zustände.
Zu Beginn der Berechnung von Schaltvorgängen steht die Aufstellung der Differentialgleichungen (DGL). Die DGL für Spannungen und Ströme basieren basieren prinzipiell auf den Kirchhoffschen Regeln: \begin {align} \text {Knotenregel:} & \qquad \sum _{j=1}^{n} i_j = 0 \qquad \text {mit $n$ Stromzweigen im Knoten}\label {eq:grundlagen:kirchhoff:knotenregel} \\ \text {Maschenregel:} & \qquad \sum _{k=1}^{m} u_k = 0 \qquad \text {mit $m$ Teilspannungen in Masche}\label {eq:grundlagen:kirchhoff:maschenregel} \end {align}
und den folgenden Strom-Spannungs-Beziehungen (Komponenten-Gl.) für \(R\), \(L\) und \(C\).: \begin {align} &\text {Widerstand:} & u_R(t) &= R \cdot i_R(t) \vphantom {\frac {\mathrm {d}}{\mathrm {d}t}} &&\label {eq:grundlagen:bauteilgleichung:widerstand}\\ &\text {Induktivität:}& u_L(t) &= L \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, i_L(t) &&\label {eq:grundlagen:bauteilgleichung:induktivitaet}\\ &\text {Kapazität:} & i_C(t) &= C \cdot \frac {\mathrm {d}}{\mathrm {d}t}\, u_C(t) &&\label {eq:grundlagen:bauteilgleichung:kapazitaet} \end {align}
In welcher Reihenfolge die Gleichungen am geschicktesten aufgestellt, umgeformt und ineinander eingesetzt werden ist abhängig von der jeweiligen Schaltungstopologie und der Zielgröße.
Ähnlich wie beim Lösen von DGLen (Vgl. Kap. 2 und Abb. 1 zu Berechnungsmethoden) kann auch beim Aufstellen der DGLen sowohl im Zeitbereich als auch im Bildbereich vorgegangen werden. Die Methode im Zeitbereich ist die in diesem Modul ausführlicher behandelte Methode. Abbildung 2 zeigt schematisch beide Vorgehensweisen im Vergleich.
Bei einfachen Schaltungen mit einer einzelnen Masche (reine Reihenschaltung) oder zwei einzelnen Knoten (reine Parallelschaltung) lassen sich die Differentialgleichungen direkt aus den Kirchhoffschen Regeln und den Bauteilgleichungen aufstellen (Zeitbereich). Gegebenenfalls muss die aufgestellte Gleichung noch differenziert werden, um die benötigten Ableitungen zu erhalten (beziehungsweise um Integrale zu entfernen). Bei komplexeren Netzwerken ist der Rechenaufwand deutlich größer.
Eine Möglichkeit den Rechenaufwand zu minimieren, ist mit Methoden der komplexen Wechselstromrechnung zu arbeiten (Bildbereich). Der Ansatz funktioniert ebenso für DC-Schaltungen, da nicht wirklich mit Frequenzen gerechnet wird. Sinn und Zweck ist die Aufstellung der DGL durch algebraische Umformung der komplexen Kirchhoffschen Regeln. Hierbei werden die Schaltungselemente durch Impedanzen respektive Admittanzen ersetzt und die zu untersuchende Größe beispielsweise durch einen komplexen Spannungsteilers bestimmt. Die Umformung zur DGL geschieht durch Rücktransformation der komplexen Größen in den Zeitbereich. \(\mathrm {j}\omega \) wird dabei durch \(\frac {\mathrm {d}}{\mathrm {d} t}\) ersetzt.
Der Vorteil des Ansatzes im Bildbereich ist, dass komplexe Spannungs- und Stromteiler anwendbar sind. Dadurch bietet sich der Ansatz vor allem bei gemischten Reihen- und Parallelschaltungen an.
Ein ähnlicher Ansatz wäre das Maschenstromverfahren in Matrixform mit komplexen Größen. [Vgl. Modul 7] Dieses wird an dieser Stelle jedoch nicht weiter betrachtet.
In allen hier untersuchten Schaltungen kommen ausschließlich folgende Komponenten zum Einsatz: Kapazitäten, Induktivitäten, ohmsche Widerstände, ideale Spannungsquellen, ideale Stromquellen, ideale elektrische Leiter und ideale Schalter. In den Schaltungen kommen keine weiteren Bauteile wie z.B. Transistoren, Dioden oder Operationsverstärker vor.
Zur Berechnung von Schaltvorgängen wird in diesem Modul stets von idealen Bauteilen in isothermen, homogenen, isotropen Medien ausgegangen. Weitere Einflüsse wie Temperaturabhängigkeiten, nichtlineare Effekte oder Ähnliches werden nicht betrachtet.
Die aufgezählten Komponenten sind alle linear und zeitinvariant. Die gleichen Eigenschaften gelten auch für Schaltungen, die sich nur diesen Komponenten zusammen setzen. Das heißt, es handelt sich um lineare, zeitinvariante Systeme (LZI-Systeme). Die Zeitinvarianz für Schalter gilt dabei eingeschränkt (abschnittsweise) für alle Zeiträume außerhalb von Schaltzeitpunkten und uneingeschränkt für alle anderen Komponenten.
Aus den Eigenschaften der Schaltungen lassen sich folgende für Eigenschaften der DGLs ableiten:
Für eine betrachtete Schaltungsgröße \(y\) in Abhängigkeit der Zeit \(t\) ergibt sich daraus die folgende Form für gewöhnliche, inhomogene, lineare DGLs mit konstanten Koeffizienten:
\begin {align} \label {eq:grundlagen:dgl:inhomogen} \sum _{i=0}^{n} a_i \cdot \frac {\mathrm{d} ^i y(t)}{\mathrm {d}t^i} = b(t)\\[2pt]\nonumber \text {mit} a_i, b(t) \in \mathbb {R}; i, n \in \mathbb {N} \end {align}
Mit der Ordnung \(n\), der Störfunktion \(b(t)\) und den konstanten Koeffizienten \(a_i\).
Der Aufbau einer Schaltung bestimmt die Form der Differentialgleichungen (DGLs) zur Beschreibung ihrer Systemgrößen (Ströme, Spannungen). Die Ordnung der DGL entspricht direkt der Anzahl an Energiespeichern, welche nicht zu einem Energiespeicher zusammengefasst werden können.[?, S. 4]
Abbildung 3 zeigt exemplarisch mehrere Schaltungen und die Ordnung der zugehörigen DGL.
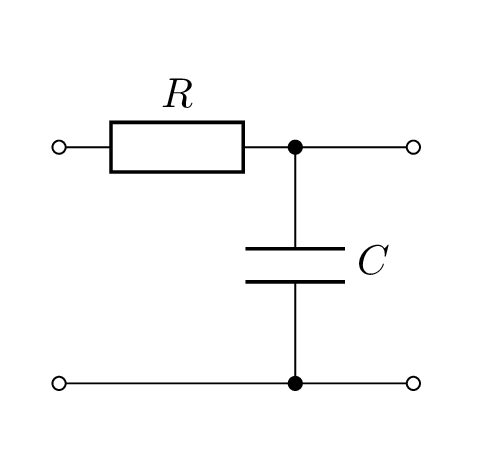

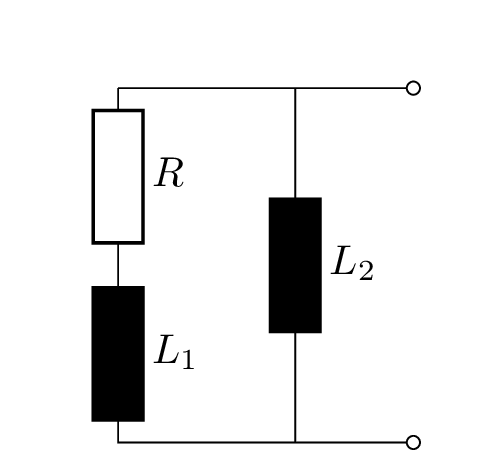
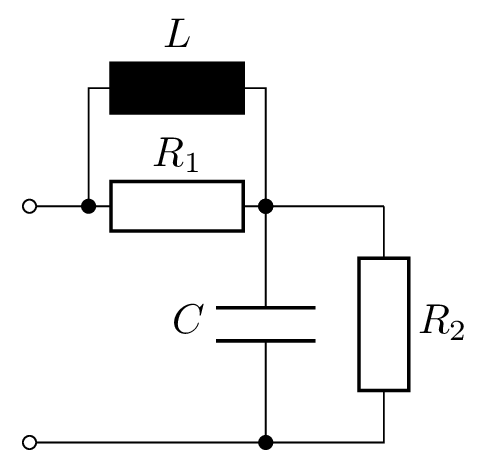
Die Ordnung der DGL bestimmt die Anzahl der Konstanten in der allgemeinen Lösung der DGL.
Die Berechnung von Schaltvorgängen im Zeitbereich basiert auf der Lösung der Differentialgleichungen (DGLs) für die Schaltungsgrößen. Allgemein exestieren für DGLs unendlich viele Lösungen.
Wichtig für die Eingrenzung der allgemeinen Lösung ist die Kenntnis der Anfangsbedingungen (AB). Die AB sind Werte von Schaltungsgrößen zu einem bestimmten Zeitpunkt \(t_0\) während des Beobachtungszeitraums (Schaltvorgang). Dabei handelt es sich beiselsweise um Spannungen oder Ströme einzelner Bauteile oder um deren Ableitungen.
Für DGL \(n\)-ter Ordnung sind \(n\) AB notwendig, um eine eindeutige Lösung zu erhalten. Sind die AB nicht explizit gegeben, können diese gegebenenfalls durch die Schaltungstopologie und den Zustand unmittelbar vor dem Schalten hergeleitet werden. Dabei ist zu unterscheiden, welche Schaltungsgrößen springen können und welche stetig sind.
Da es sich bei Induktivitäten und Kapazitäten um Energiespeicher handelt, ist deren Verhalten zu einem Zeitpunkt \(t\) abhängig von der bis dahin zu-/abgeführten Energie.
In kurzer Gegenüberstellung gilt mit \(E = \int p(t) \,\mathrm {d}t = \int u(t) \cdot i(t) \,\mathrm {d}t\) und den Gl. ?? und ??: \begin {align} \textbf {Kapazität:} && E_{el} &= \frac {1}{2} C \cdot u^2 &&\Rightarrow \qquad u = stetig && \text {(Speicher el. Energie)} \\[+4pt] \textbf {Induktivität:} && E_{mag} &= \frac {1}{2} L \cdot i^2 &&\Rightarrow \qquad i = stetig && \text {(Speicher mag. Energie)} \end {align}
Da Energie sich nur mit endlicher Geschwindigkeit bewegen kann, gilt Stetigkeit für \(u_C\) und \(i_L\): \begin {align} u_{C,t-} &= u_{C,t+} & i_{L,t-} &= i_{L,t+} \\ \text {mit} \lim _{\pm \infty \rightarrow t} u_C(t) &= u_{C,t\pm } & \lim _{\pm \infty \rightarrow t} i_L(t) &= i_{L,t\pm } \end {align}
Das bedeutet, dass die Spannung einer Kapazität ebenso wie der Strom einer Induktivität unmittelbar vor dem Schalten gleich groß ist wie zu Beginn des folgenden Schaltvorganges.
Der sich ergebende Zeitverlauf einer Größe \(y(t)\) kann während eines Ausgleichsvorgangs zerlegt werden in einen flüchtigen Zustand \(y_f\) und in einen eingeschwungenen Zustand \(y_e\). \begin {equation} \label {eq:grundlagen:zerlegung} y(t) := y_{\mathrm {f}}(t) + y_{\mathrm {e}}(t) \end {equation} Der eingeschwungene Zustand \(y_{\mathrm {e}}\) beschreibt den stationäre Zustand, den die Größe \(y\) anstrebt. Der flüchtige Zustand \(y_{\mathrm {f}}\), auch freier Zustand genannt, repräsentiert den abklingenden Teil von \(y\): \begin {align} \lim _{t \to \infty } y_{\mathrm {e}}(t) &= \lim _{t \to \infty } y(t) & y_{\mathrm {e}} &= \text {stationär} \label {eq:grundlagen:eingeschwungen}\\ \lim _{t \to \infty } y_{\mathrm {f}}(t) &= 0 & y_{\mathrm {f}} &= y - y_{\mathrm {e}} \label {eq:grundlagen:fluechtig} \end {align}
Abbildung 4 zeigt exemplarisch einen Ausgleichsvorgang mit Zerlegung einer Größe \(y(t)\) in einen flüchtigen und eingeschwungenen Zustand. Die Darstellung entspricht dem Spannungsverlauf einer Kapazität beim Laden mit Gleichspannung über einen ohmschen Widerstand wie in Beispiel ??.
Da die Größe \(y(t)\) nach Gleichung ?? für \(t \to \infty \) in \(y_e(t)\) übergeht, muss \(y_e(t)\) ebenfalls die DGL aus Gleichung ?? inklusive Störterm \(b\) erfüllen: \begin {align} \label {eq:grundlagen:dgl:eingeschwungen} \sum _{i=0}^{n} a_i \cdot \frac {\mathrm{d} ^i(t)}{\mathrm {d}t^i}\,y_{\mathrm {e}} &= b(t) \end {align}
Ziehen wir die DGL für \(y_e\) aus Gl. ?? von der allgemeinen inhomogenen DGL aus Gl. ?? ab, erhalten wir mit der Zerlegung nach Gl. 1 die homogene DGL für den flüchtigen Zustand: \begin {align} \label {eq:grundlagen:dgl:fluechtig} \sum _{i=0}^{n} a_i \cdot \frac {\mathrm{d} ^i(t)}{\mathrm {d}t^i}\,y_{\mathrm {f}} = 0 \end {align}
Mathematisch entspricht die Zerlegung des Zeitverlaufs \(y(t)\) in einen flüchtigen und eingeschwungenen Zustand der Zerlegung der Lösung der inhomogenen DGL \(y\) in die Lösung der homogenen DGL \(y_{\mathrm {h}}\) (ohne Störterm) und in eine partikuläre Lösung \(y_{\mathrm {p}}\) der inhomogenen DGL mit: \begin {align} \text {homogene Lösung}\qquad y_{\mathrm {h}} &= y_{\mathrm {f}} \qquad \text {flüchtiger Zustand}\\ \text {partikuläre Lösung}\qquad y_{\mathrm {p}} &= y_{\mathrm {e}} \qquad \text {eingeschw. Zustand} \end {align}
Die Zerlegung von Ausgleichsvorgängen in einen eingeschwungenen und einen flüchtigen Zustand findet sich in ähnlicher Form in den Lehrbüchern von Albach[?], Hagmann[?] und Weißgerber[?].
Für die Lösung von gewöhnlicher, linearer, homogener DGLen mit konstanten Koeffizienten der Form:
\begin {equation} \label {eq:grundlagen:dgl:homogen} \sum _{i=0}^{n} a_i \cdot \frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\, y_{\mathrm {h}} = 0 \end {equation}
wird in der Regel der Ansatz einer Exponentialfunktion verwendet:
\begin {equation} \label {eq:grundlagen:dglexponentialansatz} y_{\mathrm {h}}(t) = K \cdot \mathrm {e}^{\lambda t} \end {equation}
Dabei ist \(K\) eine Konstante und \(\lambda \) die Lösung des charakteristischen Polynoms und wird auch als Eigenwert bezeichnet. Durch Einsetzen des Exponential-Ansatzes in 2, Differenzieren und Ausklammern: \begin {align} \sum _{i=0}^{n} a_i \cdot \frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\, K \cdot \mathrm {e}^{\lambda t} &= 0 \nonumber \\[2pt] \left (\sum _{i=0}^{n} a_i \cdot \lambda ^i \right ) K \cdot \mathrm {e}^{\lambda t} &= 0 \nonumber \\[4pt] \end {align}
kann das charakteristische Polynom aufgestellt werden: \begin {align} \sum _{i=0}^{n} a_i \cdot \lambda ^i &= 0 \end {align}
Die maximale Anzahl an Eigenwerten ist gegeben durch die Ordnung einer DGL. Da die Koeffizienten \(a_i\) reell sind, müssen die Eigenwerte \(\lambda _i\) ebenfalls reell sein, oder paarweise komplex konjugiert.
Bedingung: Um die homogene Differentialgleichung in Gleichung 2 zu erfüllen, muss der Realteil aller Eigenwerte negativ sein \(\Re \{\underline {\lambda }_i\}<0\). Nur dann konvergieren die Exponentialterme aus dem Ansatz in Gleichung 3 für \(t \to \infty \).
Die allgemeine homogene Lösung \(y_{\mathrm {h}}\) einer DGL \(n\)-ter Ordnung ist die Linearkombination von \(n\) linear unabhängigen Lösungen der homogenen DGL.
Die Form der Lösung hängt davon ab, ob es sich um unterschiedliche Eigenwerte, gleiche Eigenwerte (Mehrfache Nullstellen des charakteristischen Polynoms) oder paarweise komplex konjugierte Eigenwerte handelt.
Sind alle Eigenwerte \(\lambda _i\) verschieden, ergibt sich die homogene Lösung zu: \begin {equation} \label {eq:grundlagen:homogeneloesung:lambdaungleich} y_{\mathrm {h}}(t) = \sum _{i=1}^{n} K_i \cdot \mathrm {e}^{\lambda _i t} \qquad \text {für} \lambda _i \neq \lambda _j \ \forall \ i,j \end {equation} Bei paarweise komplex konjugierten Eigenwerten kann diese Lösung umformuliert werden. [Herleitung in Abschnitt ??.] Für \(\lambda _1 = \lambda _2^* = a + \mathrm {j} b \in \mathbb {C}\) ergibt sich für die homogene Lösung: \begin {equation} \label {eq:grundlagen:homogeneloesung:lambdakomplex} \begin {aligned} y_{\mathrm {h}}(t) &= K_1 \cdot \mathrm {e}^{a \cdot t} \cdot \cos (b \cdot t) + K_2 \cdot \mathrm {e}^{a \cdot t} \cdot \sin (b \cdot t) \\ &= C_0 \cdot \mathrm {e}^{a \cdot t} \cdot \cos (b \cdot t + \varphi _0) \end {aligned} \end {equation} Sind alle Eigenwerte \(\lambda _i\) gleich ergibt sich die homogene Lösung zu: \begin {equation} \label {eq:grundlagen:homogeneloesung:lambdagleich} y_{\mathrm {h}}(t) = \sum _{i=1}^{n} K_i \cdot t^{i-1} \cdot \mathrm {e}^{\lambda t} \qquad \text {für} \lambda = \lambda _i \ \forall \ i \end {equation} Bei gemischten Nullstellen ergibt sich die Lösung aus einer Kombination der obigen Lösungen wie in Beispiel ?? gezeigt ist.
Beispiel 1: Linear unabhängige Lösungen einer DGL
Dieses Beispiel ist nahezu unverändert übernommen aus [?, S. 241]. Gesucht ist die allgemeine Lösung der folgenden homogenen DGL 5. Ordnung: \begin {equation*} \frac {\mathrm {d}^{5}}{\mathrm {d}t^{5}} y(t) + 7 \frac {\mathrm {d}^{4}}{\mathrm {d}t^{4}} y(t) + 26 \frac {\mathrm {d}^{3}}{\mathrm {d}t^{3}} y(t) + 62 \frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} y(t) + 8 \frac {\mathrm {d}}{\mathrm {d}t} y(t) + 75 y(t) = 0 \end {equation*} Das charakteristische Polynom: \begin {equation*} \lambda ^{5} + 7 \cdot \lambda ^{4} + 26 \cdot \lambda ^{3} + 62 \cdot \lambda ^{2} + 85 \cdot \lambda + 75 = 0 \end {equation*} besitzt eine einfache und zwei doppelte, konjugierte, komplexe Nullstellen: \begin {equation*} \lambda _1 = -3, \lambda _2 = \lambda _3 = -1+\mathrm {2j}, \lambda _4 = \lambda _5 = -1-\mathrm {2j} \end {equation*} Mit den Ansätzen aus Gl. 4, 5 und 6 ergibt sich die allgemeine Lösung zu: \begin {equation*} y_{\mathrm {h}}(t) = K_1 \cdot \mathrm {e}^{-3 t} + (K_2 + K_3 \cdot t) \cdot \mathrm {e}^{-t} \sin (2t) + (K_4 + K_5 \cdot t) \cdot \mathrm {e}^{-t} \cos (2t) \end {equation*}
Für die Berechnung einer partikulären Lösung \(y_{\mathrm {p}}\) einer inhomogenen DGL können verschiedene Methoden gewählt werden. Eine Möglichkeit ist einen Lösungsansatz ähnlich der Anregung zu wählen.
Speziell für Schaltvorgänge gilt, dass \(y_{\mathrm {p}}\) dem eingeschwungenen Zustand entspricht wie in Abs. 4.1 hergeleitet wurde. Daraus folgt für lineare, zeitinvariante Schaltelementen:
Die Bestimmung kann durch Methoden der statischen Netzwerkberechnung erfolgen. Hierfür reichen die Kirchhoffschen Regeln, die Gleichungen für die Bauelemente \(R\), \(L\) und \(C\) und den daraus resultierenden Strom- und Spannungsteilerregeln. Für Wechselgrößen werden die komplexen Wechselstrom-Äquivalente der aufgezählten Methoden verwendet.
Transformation von DGLen sinusförmiger Größen in den komplexen Zahlenraum:
Da bei AC-Anregung die DGL ?? für den eingeschwungenen Zustand für Wechselgrößen gilt, kann die DGL in den komplexen Zahlenraum transformiert werden. Das Vorgehen entspricht der Transformation der differentiellen Strom- und Spannungsbeziehungen für \(R\), \(L\) und \(C\) zu deren komplexen Strom- und Spannungsbeziehungen anhand deren jeweiligen Impedanz \(\underline {Z}\) respektive Admittanz \(\underline {Y}\).
Eine sinusförmige Größe \(y(t)\) mit Amplitude \(\hat {Y}\) und einem Nullphasenwinkel \(\varphi \) lässt sich mit komplexem Amplitudenzeiger (Phasor) \(\underline {\hat {Y}}\) wie folgt beschreiben [Vgl. Modul 7]: \begin {align*} y(t) &= \hat {Y} \cdot \cos (\omega t + \varphi ) = \Re \left \{ \underline {\hat {Y}} \cdot \mathrm {e}^{\mathrm {j} \omega t} \right \} & &\Longleftrightarrow & \underline {\hat {Y}} &= \hat {Y} \cdot \mathrm {e}^{\mathrm {j} \varphi } \vphantom {\bigg |}\\ \end {align*}
Ableitungen nach der Zeit \(\frac {\mathrm {d}}{\mathrm {d}t}\) werden im komplexen Zahlenraum durch \(\mathrm {j} \omega \) ersetzt: \begin {align*} \frac {\mathrm {d}}{\mathrm {d}t} y(t) &= \hat {Y} \cdot \omega \cdot \cos (\omega t + \varphi + \frac {\pi }{2}) & &\Longleftrightarrow & \mathrm {j} \omega \cdot \underline {\hat {Y}} &= \hat {Y} \cdot \omega \cdot \mathrm {e}^{\mathrm {j} \left (\varphi + \frac {\pi }{2}\right )} \end {align*}
Der Faktor \(\mathrm {j}\omega \) entspricht rücktransformiert dem Vorfaktor \(\omega \) und einer Phasenverschiebung von \(1/{\pi }{2}\). Dadurch gilt allgemein bei DGLen sinusförmiger Größen (Index \(ac\)) der Form in Gleichung ??: \begin {equation} \sum _{i=0}^n a_i \cdot \left (\frac {\mathrm {d}}{\mathrm {d}t}\right )^i y_{ac} = b_{ac} \qquad \Longleftrightarrow \qquad \sum _{i=0}^n a_i \cdot \left (\mathrm {j}\omega \right )^i \cdot \underline {\hat {Y}} = \underline {\hat {B}} \label {eq:grundlagen:dgl:komplex} \end {equation} Alternativ kann auch der Imaginärteil komplexer Amplitudenzeiger zur Darstellung von sinusförmiger Wechselgrößen verwendet werden. [Vergleich Modul 7 - Periodische Größen]
Das Berechnen von Ausgleichsvorgängen im Zeitbereich besteht zum einen im Aufstellen einer passenden DGL und zum anderen auf dem Lösen der aufgestellten DGL. Merkbox 16 fasst die die Berechnung von Ausgleichsvorgängen im Zeitbereich zu fünf Schritten zusammen. Die Schritte sind stark angelehnt die Vorgehensweise von Weißgerber [?, S. 6].
Merke: Verfahren für DGL
\begin {equation*} \,^{*}\text {mit}\qquad K_i^{'} = \left \{ \begin {aligned} &K_i \hphantom {{}\cdot t^{k}} \qquad \text {für}{ \lambda _i \neq \lambda _j \qquad \forall i,j }\hspace {5cm}\text {(einfache NS)}\\ &K_i \cdot t^{k} \qquad \text {für}{ \lambda _{i} = \lambda _{i-k} \text {mit} k \in [0,\ 1,\ \mathrm{d}ots ,\ m{-}1] }\hspace {5cm}\text {($m$-fache NS, $k$-ter gleicher EW)}\end {aligned} \right . \end {equation*}
Die Reihenfolge der Schritte 2. und 3. ist prinzipiell beliebig. In der Mathematik ist die gezeigte Reihenfolge üblicher mit der Bestimmung der allgemeinen homogenen Lösung vor der Lösung der partikulären Lösung(en). Aus elektrotechnischer Sicht kann es sich anbieten zunächst die den eingeschwungenen Zustand (partikuläre Lösung) zu bestimmen.
...