Im Modul 12
Schaltvorgänge im Zeitbereich berechnen
In diesem Kapitel werden Schaltvorgänge in elektrischen Schaltungen im Zeitbereich betrachtet. Es wird zwischen Schaltvorgängen bei Gleichspannung und Wechselspannung unterschieden. Die Betrachtung erfolgt für RC- und RL-Glieder, sowie RLC-Glieder.
Lernziele: Schaltvorgänge
Studierende lernen:
In diesem Kapitel werden Lade- und Entladevorgänge von Kapazitäten und Induktivitäten jeweils in Reihe mit einem Widerstand bei Gleichspannung berechnet und dargestellt.
Schaltvorgänge bei sinusförmiger Anregung folgen in Kapitel 2.
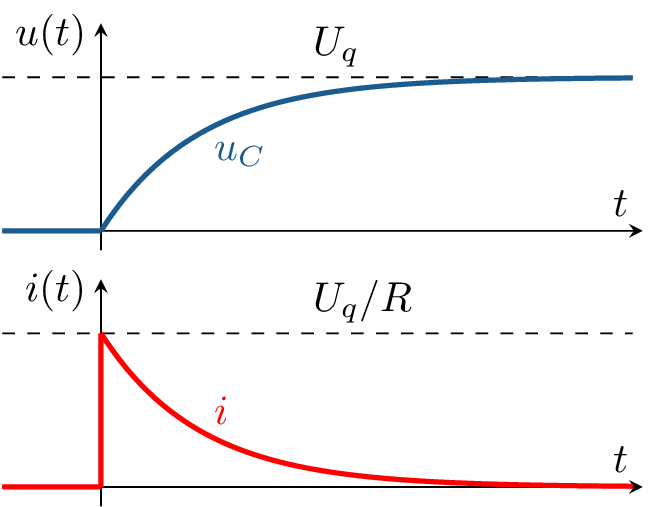
Beispiel ?? zeigt den Rechenweg zur Bestimmung des Spannungsverlaufs \(u_C(t)\) einer zu Beginn entladenen Kapazität \(C\) beim Laden mit Gleichspannung für \(t \geq 0\) über einen Widerstand \(R\) und den Zeitverlauf des Ladestroms \(i(t)\). Die angewandte Berechnungsmethode entspricht dem Verfahren für DGL im Zeitbereich nach Merksatz ??.
Aus den Ergebnissen ablesen lässt sich die exponentielle Annäherung von \(u_C(t)\) an die Anregung \(U_q\): \begin {align} u_C(t) &= U_q \cdot \left ( 1 - \mathrm {e}^{-1/{t}{\tau }} \right ) \end {align}
und der exponentielle Abfall von \(i(t)\) respektive \(u_R(t)\) ab deren Maximalwerten \(U_q/R\) und \(U_q\): \begin {align} i(t) &= \frac {U_q}{R} \cdot \mathrm {e}^{-1/{t}{\tau }}\\[4pt] u_R(t) &= U_q \cdot \mathrm {e}^{-1/{t}{\tau }} \end {align}
bis die Kapazität geladen ist. Die Zeitkonstante \(\tau \) bestimmt die Steilheit der exponentiellen Verläufe. Für das RC-Glied ergibt sich \(\tau = RC\). Die Einheit für \(\tau \) ist gleich jener der Zeit.
| \(t\) | \(\tau \) | \(3\,\tau \) | \(5\,\tau \) |
| \(1 - \mathrm {e}^{-t/\tau }\) | \(63,2\%\) | \(95,0\%\) | \(99,3\%\) \(\vphantom {\big |}\) |
| \( \mathrm {e}^{-t/\tau }\) | \(36,8\%\) | \(5,0\%\) | \(0,7\%\) \(\vphantom {\big |}\) |
Faustregel: „Eingeschwungen“ nach \(5\,\tau \)
Wie in Abbildung 1 dargestellt, schneidet die Tangente von \(u_C\) im Punkt \(u_C(t=0)\) den Endwert \(U_q\) zum Zeitpunkt \(t=\tau \). Allgemein gilt in jedem Punkt exponentieller Annäherungen/Abfälle, dass die Tangete den Endwert nach \(\tau \) erreicht.
Tabelle 1 zeigt typische Werte für exponentielle Annäherungen/Abfälle nach Vielfachen von \(\tau \). Die Werte sind relativ zum Maximalwert (Start- oder angestrebter Grenzwert). Als „eingeschwungen“ gilt ein solcher Verlauf nach \(5\,\tau \).
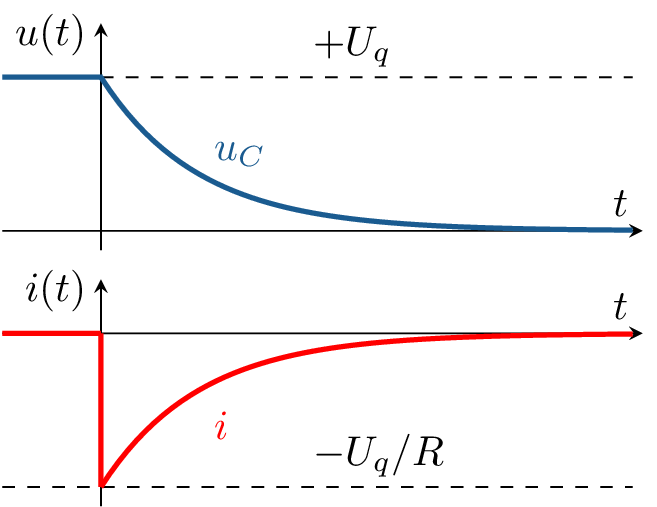
Beispiel ?? zeigt den Rechenweg zur Bestimmung des Spannungsverlaufs \(u_C(t)\) einer Kapazität \(C\) beim Entladen über einen Widerstand \(R\) und zugehörige Zeitverläufe. Hierbei ergeben sich analog zum Ladevorgang exponentielle Verläufe mit gleicher Zeitkonstante, jedoch mit unterschiedlichen Start- und Endwerten.
Der Rechenweg in den Beispielen ?? und ?? ist prinzipiell identisch. Beim Lade- und Entladevorgang unterscheiden sich lediglich die Anfangsbedingung \(u_C(0)\) (bei Schaltzeitpuntk \(t=0\)) und die Randbedingung \(u_{C,\mathrm {e}}\) (für \(t \to \infty \)). Dadurch ergeben sich unterschiedliche partikuläre Lösungen und andere Konstanten \(K\) in der allgemeinen Lösung.
Verallgemeinert lässt sich der Spannungsverlauf \(u_C\) einer Kapazität \(C\) beim Laden/Entladen mit Gleichspannung über einen Widerstand \(R\) ab einem Schaltzeitpunkt \(t_0\) beschreiben durch: \begin {equation} \label {eq:rc:charge:dc:allg:parthom} u_C(t-t_0) = \underbrace { u_{C,\mathrm {e}} \vphantom {\Big |}}_{u_{C,\mathrm {p}}} + \underbrace { \big (u_C(t_0)-u_{C,\mathrm e}\big ) \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} \vphantom {\Big |}}_{u_{C,\mathrm {h}}} \end {equation} Etwas umgeschrieben lässt sich der Spannungsverlauf auch recht anschaulich wie folgt formulieren: \begin {equation} \label {eq:rc:charge:dc:allg:startend} u_C(t-t_0) = \underbrace {u_C(t_0) \vphantom {\Big |}}_{\text {Startwert}} + \big (\underbrace {u_{C,\mathrm e} - u_C(t_0) \vphantom {\Big |}}_{\text {Differenz}}\big ) \cdot \bigg ( \underbrace { 1- \mathrm {e}^{-\frac {t-t_0}{\tau }} \vphantom {\Big |}}_{\text {\clap {Exp. Annäherung}}} \bigg ) \end {equation} Die allgemeine Lösung in Gleichung 1 beziehungsweise 2 gilt nur für Anregungen mit Gleichgröße. Die Lösung ist typisch für verlustbehaftete, lineare Systeme erster Ordnung (mit einem Energiespeicher), weshalb sie in ähnlicher Form auch bei RL-Gliedern auftritt.
Exkurs: DGL 1. Ordnung und Zeitkonstante \(\tau \)
Die Exponentialform ist typisch für lineare Systeme erster Ordnung mit Energiespeicher und ergibt sich aus der Lösung der linearen, gewöhnlichen DGL 1. Ordnung mit konstanten Koeffizienten. Durch Umformung (\(a_0=1\)) lässt sich die Zeitkonstante \(\tau \) direkt aus der DGL ablesen (\(a_1=\tau \)).: \begin {equation} \label {eq:dgl:tau} \tau \cdot \frac {\mathrm {d}}{\mathrm {d}t}\,y(t) + y(t) = b(t) \end {equation} Dadurch lässt sich die homogene Lösung direkt angeben mit.: \begin {equation} y_{\mathrm {h}}(t) = K\cdot \mathrm {e}^{-\frac {t}{\tau }} \end {equation} Die Zeitkonstante ist ein Maß für die Schnelligkeit, mit der ein System auf eine Änderung reagiert.
Beispiel 1: RC-Glied DC-Ladevorgang
Bestimmung von Spannung \(u_C\) und Ladestrom \(i\) der Kapazität \(C\) beim Laden über Widerstand \(R\) mit Gleichspannung \(U_q\) für \(t \geq 0\). Die Kapazität ist zu Beginn entladen.
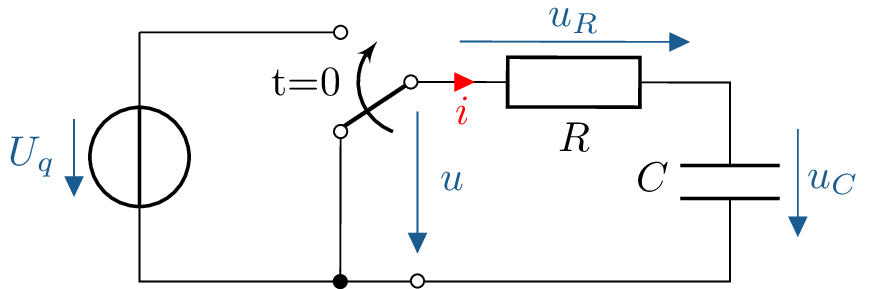 \begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ C \\ \text {gesucht:}&& &i(t), u_L(t) \end {aligned} \end {equation*}
\begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ C \\ \text {gesucht:}&& &i(t), u_L(t) \end {aligned} \end {equation*}
1.) DGL aufstellen: von \(u_C(t)\) für \(t>0\)
Ausgehend von der Maschengleichung wird \(u_R\) in Abhängigkeit von \(u_C\) ausgedrückt:\begin {align*} &\text {Masche}:&&& u_R + u_C &= U_q&&& &\text {mit} u_R = R \cdot i \\ &&&& R \cdot {\color {red} i} + u_C &= U_q&&& &\text {mit} i = C \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C \\ &\text {DGL}:&&& R \cdot C \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C + u_C &= U_q \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
2.) Homogene Lösung, allg.: (flüchtig) (ohne Störterm)\begin {align*} &\text {DGL}_{h}:&&& RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_{C,\mathrm {h}} + u_{C,\mathrm {h}} &= 0 &&& &\text {Ansatz:} u_{C,\mathrm {h}} = K \cdot \mathrm {e}^{\lambda t}\\ &&&& K \cdot (RC \cdot \lambda \mathrm {e}^{\lambda t}\ +\ \mathrm {e}^{\lambda t}) &= 0 \\ &\text {char. Pol.:}&&& RC \cdot \lambda + 1 &= 0 &&& &\Rightarrow \lambda = -\frac {1}{\tau } = -\frac {1}{RC}\\ &\text {hom. Lsg.}:&&& u_{C,\mathrm {h}} = K \cdot \mathrm {e}^{-1/{t}{\tau }}&&&& &\text {mit} \tau = RC \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
3.) Partikulare Lösung: (eingeschwungen) (für \(t \to \infty \))\begin {align*} &\text {DGL}_{p}:&&& \cancel {RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_{C,p}} + u_{C,p} &= U_q &&& &\text {mit} u_{C,p} = konst. \\ &\text {part. Lsg.}:&&& u_{C,p} &= U_q \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
4.) Inhomogene Lösung, allg.: (Überlagerung)\begin {align*} &&&& u_C(t) &= u_{C,\mathrm {h}}(t) + u_{C,p}(t) &&& &u_C(t)= u_{C,f}(t) + u_{C,e}(t) \\ &\text {allg. Lsg.:}&&& u_C(t) &= K \cdot \mathrm {e}^{-1/{t}{\tau }} + U_q \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
5.) Konstanten bestimmen: (Anfangsbedingungen einsetzen)\begin {align*} &\text {Anfangsbed.}&&& u_C(0) &= K + U_q \overset {!}{=} \frac {0}{1} &&& &\Rightarrow K = -U_q \\ &&&& u_C(t) &= -U_q \cdot \mathrm {e}^{-1/{t}{\tau }} + U_q \\ &\text {spez. allg. Lsg.:}&&& u_C(t) &= U_q \left ( 1 - \mathrm {e}^{-1/{t}{\tau }} \right ) \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Strom \(i\) aus Spannung \(u_C\) bestimmen:\begin {align*} &\text {Strom:}&&& i &= \frac {U_q}{R} \cdot \mathrm {e}^{-1/{t}{\tau }} &&& &\text {mit} i = C \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Beispiel 2: RC-Glied Entladevorgang
Bestimmung von Spannung \(u_C\) und Strom \(i_C\) einer Kapazität \(C\) beim Entladen über einen Widerstand \(R\) für \(t \geq 0\). Die Kapazität ist zu Beginn geladen auf \(U_q\).
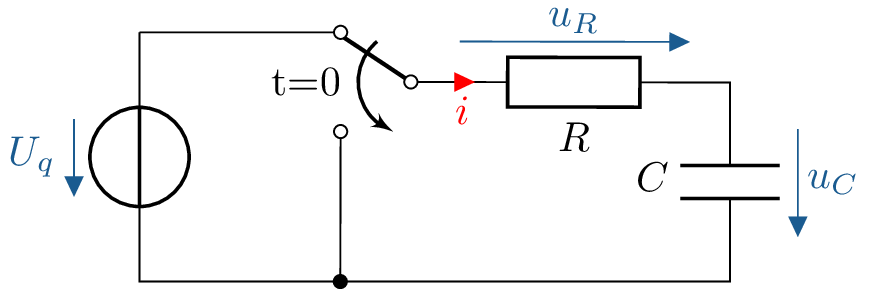 \begin {equation*} \begin {aligned} &\text {gegeben:}& &u_C(0),\ U_q,\ R,\ C \\ &\text {gesucht:}& &u_C(t) \end {aligned} \end {equation*}
\begin {equation*} \begin {aligned} &\text {gegeben:}& &u_C(0),\ U_q,\ R,\ C \\ &\text {gesucht:}& &u_C(t) \end {aligned} \end {equation*}
1.) DGL aufstellen: von \(u_C(t)\) für \(t>0\), analog zu Beispiel ?? \begin {align*} &\text {Masche}:&&& u_R + u_C &= 0&&& &\text {mit} u_R = R \cdot i \\ &\text {DGL}:&&& RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C + u_C &= 0 &&& &\text {mit} i = C \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
2.) Homogene Lösung, allg.: (flüchtig) Identisch zu Beispiel ??\begin {align*} &\text {hom. Lsg.}:&&& u_{C,\mathrm {h}} = K \cdot \mathrm {e}^{-1/{t}{\tau }}&&&& &\text {mit} \tau = RC \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Die partiklare Lösung \(u_{C,p}\) entfällt, da \(u_C\) eingeschwungen (\(t \to \infty \)) null wird.
3. Part. Lsg.: (eingeschwungen) und 4. Überlagerung:\begin {align*} &\text {allg. Lsg.:}&&& u_C &= u_{C,\mathrm {h}} + \cancel {u_{C,p}}&&& &\text {mit} u_{C,p}=0 \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
5.) Konstanten bestimmen: (Anfangsbedingungen einsetzen)\begin {align*} &\text {Anfangsbed.}&&& u_C(0) &= K \cdot \mathrm {e}^{0} \overset {!}{=} U_q &&&& \Rightarrow K = U_q\\ &\text {spez. allg. Lsg.:}&&& u_C(t) &= U_q \cdot \mathrm {e}^{-1/{t}{\tau }} \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Strom \(i\) aus Spannung \(u_C\) bestimmen:\begin {align*} &\text {Strom:}&&& i &= - \frac {U_q}{R} \cdot \mathrm {e}^{-1/{t}{\tau }} &&& &\text {mit} i = C \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Der Rechenweg zur Bestimmung des Strom- oder Spannungsverlaufs bei Induktivitäten bei Anregung mit Gleichspannung ist identisch zu der Berechnung bei Kapazitäten in Kapitel 1.1. Das sich einstellende Zeitverhalten mit Exponentialverläufen und Zeitkonstanten ist analog zu dem dort beschriebenen.
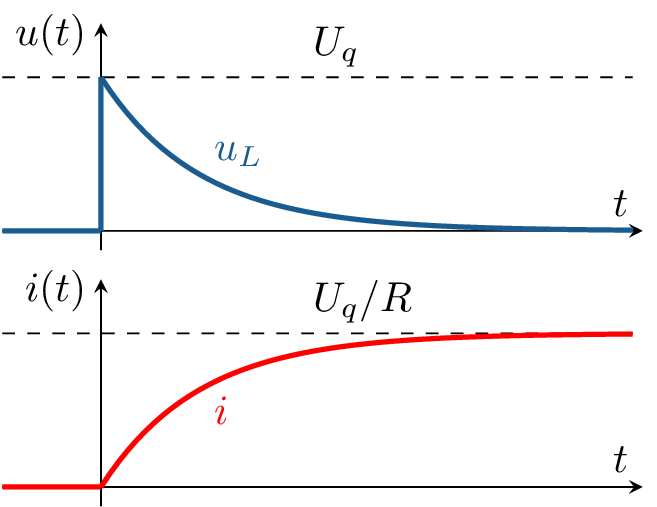
Exemplarisch ist in Beispiel ?? und ?? der Ladestrom \(i(t)\) und die Induktivitätsspannung \(u_L(t)\) einer Induktivität \(L\) beim Laden über einen Widerstand \(R\) mit Gleichspannung \(U_q\) für \(t \geq 0\) berechnet und dargestellt.
Die Beispiele unterscheiden sich lediglich im Rechenweg. In Beispiel ?? wird die DGL für \(i(t)\) und in Beispiel ?? für \(u_L(t)\) aufgestellt und gelöst.
Beispiel 3: RL-Glied DC-Ladevorgang - Über DGL von \(i\)
Bestimmung von Ladestrom \(i\) und Spannung \(u_L\) der Induktivität \(L\) beim Laden über Widerstand \(R\) mit Gleichspannung \(U_q\) ab Schalzeitpunkt \(t=0\). Zuvor fließt kein Strom.
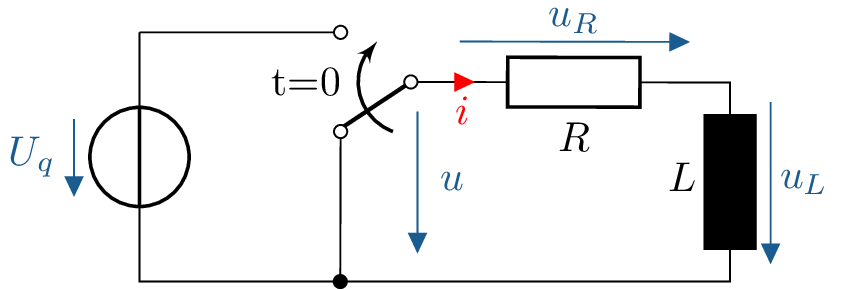 \begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ L \\ \text {gesucht:}&& &u_L(t),\ i(t) \end {aligned} \end {equation*}
\begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ L \\ \text {gesucht:}&& &u_L(t),\ i(t) \end {aligned} \end {equation*}
1.) DGL aufstellen: von \(i(t)\) für \(t \geq 0\)
Ausgehend von der Maschengleichung wird \(u_R\) und \(u_L\) nach \(i\) umgeschrieben:\begin {align*} &\text {Masche}:&&& u_R + u_L &= U_q&&& &\text {mit} u_R = R \cdot i \\ &&&& R \cdot i + L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i &= U_q &&& &\text {mit} u_L = L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i \\ &\text {DGL}:&&& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} i + i &= \frac {U_q}{R} \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
2.) Homogene Lösung, allg.: (flüchtig) (ohne Störterm)\begin {align*} &\text {DGL}_{h}:&&& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} i_{\mathrm h} + i_{\mathrm h} &= 0 &&& &\text {Ansatz:} i_{\mathrm h} = K \cdot \mathrm {e}^{\lambda t}\\ &\text {char. Pol.:}&&& \frac {L}{R} \cdot \lambda + 1 &= 0 &&& &\Rightarrow \lambda = -\frac {1}{\tau } = -\frac {R}{L}\\ &\text {hom. Lsg.}:&&& i_{\mathrm h} &= K \cdot \mathrm {e}^{-1/{t}{\tau }}&&& &\text {mit} \tau = \frac {L}{R} \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
3.) Partikulare Lösung: (eingeschwungen) mit \(t \to \infty \)\begin {align*} &\text {DGL}_{p}:&&& \cancel {\frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} i_{\mathrm p}} + i_{\mathrm p} &= \frac {U_q}{R} &&& &\text {mit} i_{\mathrm p} = konst. \\ &\text {part. Lsg.}:&&& i_{\mathrm p} &= \frac {U_q}{R} \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
4.) Inhomogene Lösung, allg.: (Überlagerung)\begin {align*} &\text {allg. Lsg.:}&&& i(t) &= \underbrace {K \cdot \mathrm {e}^{-1/{t}{\tau }} \vphantom {\frac {U_q}{R}}}_{i_{\mathrm h}} + \underbrace { \frac {U_q}{R} }_{i_{\mathrm p}} &&& &\text {mit} i_{\mathrm h}=i_f, i_{\mathrm p}=i_e \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
5.) Konstanten bestimmen: (Anfangsbedingungen einsetzen)\begin {align*} &\text {Anfangsbed.}&&& i(0) &= K \cdot \cancel {\mathrm {e}^0} + \frac {U_q}{R} \overset {!}{=} 0 &&& &\Rightarrow K = -\frac {U_q}{R}\\ &\text {eindeut. Lsg.:}&&& i(t) &= \frac {U_q}{R} \cdot \left ( 1 - \mathrm {e}^{-1/{t}{\tau }} \right ) \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
Spannung \(u_L\) aus Strom \(i\) bestimmen:\begin {align*} &\text {Spannung:}&&& u_L &= U_q \cdot \mathrm {e}^{-1/{t}{\tau }} &&& &\text {mit} u_L = L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooo}\nonumber \end {align*}
Beispiel 4: RL-Glied DC-Ladevorgang - Über DGL von \(u_L\)
Bestimmung von Spannung \(u_L\) und Ladestrom \(i\) der Induktivität \(L\) beim Laden über Widerstand \(R\) mit Gleichspannung \(U_q\) für \(t \geq 0\). Der Stromkreis ist vor \(t=0\) unterbrochen.
 \begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ L \\ \text {gesucht:}&& &u_L(t),\ i(t) \end {aligned} \end {equation*}
\begin {equation*} \begin {aligned} \text {gegeben:}&& &i(0),\ U_q,\ R,\ L \\ \text {gesucht:}&& &u_L(t),\ i(t) \end {aligned} \end {equation*}
1.) DGL aufstellen: von \(u_L(t)\) für \(t \geq 0\)
Ausgehend von der Maschengleichung wird \(u_R\) in Abhängigkeit von \(u_L\) ausgedrückt:\begin {align*} &\text {Masche}:&&& u_R + u_L &= U_q&&& &\text {mit} u_R = R \cdot i \\ &&&& R \cdot i + u_L &= U_q &&& &\left | \cdot \frac {\mathrm {d}}{\mathrm {d}t} \right . \\ &&&& R \cdot \frac {u_L}{L} + \frac {\mathrm {d}}{\mathrm {d}t} u_L &= \frac {\mathrm {d}}{\mathrm {d}t} U_q &&& &\text {mit} u_L = L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i \\ &\text {DGL}:&&& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_L + u_L &= 0 \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
2.) Homogene Lösung, allg.: (flüchtig) (ohne Störterm)\begin {align*} &\text {DGL}_{h}:&&& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_{L,h} + u_{L,h} &= 0 &&& &\text {Ansatz:} u_{L,h} = K \cdot \mathrm {e}^{\lambda t}\\ &\text {char. Pol.:}&&& \frac {L}{R} \cdot \lambda + 1 &= 0 &&& &\Rightarrow \lambda = -\frac {1}{\tau } = -\frac {R}{L}\\ &\text {hom. Lsg.}:&&& u_{L,h} = K \cdot \mathrm {e}^{-1/{t}{\tau }}&&&& &\text {mit} \tau = \frac {L}{R} \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
3.) Partikulare Lösung: (eingeschwungen) mit \(t \to \infty \)\begin {align*} &\text {DGL}_{p}:&&& \cancel {\frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_{L,p}} + u_{L,p} &= 0 &&& &\text {mit} u_{L,p} = konst. \\ &\text {part. Lsg.}:&&& u_{L,p} &= 0 \\[-15pt]&\hphantom {R1ooooooo}&&&\hphantom {L3oooooooooooooooooooo}&\hphantom {R3ooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
4.) Inhomogene Lösung, allg.: (Überlagerung)\begin {align*} &&&& u_L(t) &= u_{L,h}(t) + \cancel {u_{L,p}(t)} &&& &u_L(t)= u_{L,f}(t) + \cancel {u_{L,e}(t)} \\ &\text {allg. Lsg.:}&&& u_L(t) &= K \cdot \mathrm {e}^{-1/{t}{\tau }} \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
5.) Konstanten bestimmen: (Anfangsbedingungen einsetzen)\begin {align*} &\text {Anfangsbed.}&&& i(0) &= \frac {u_R(0)}{R} \overset {!}{=} 0 &&& &\Rightarrow u_L(0) = U_q - \cancel {u_R(0)}\\ &&&& u_L(0) &= K \cdot \mathrm {e}^{-0} \overset {!}{=} U_q &&& &\Rightarrow K = U_q\\ &\text {eindeut. Lsg.:}&&& u_L(t) &= U_q \cdot \mathrm {e}^{-1/{t}{\tau }} \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Strom \(i\) aus Spannung \(u_L\) bestimmen:\begin {align*} &\text {Strom:}&&& i &= \frac {U_q}{R} \cdot \left ( 1 - \mathrm {e}^{-1/{t}{\tau }} \right ) &&& &\text {mit} i = \frac {u_R}{R} = \frac {U_q - u_L}{R} \\[-15pt]&\hphantom {R1oooooooooooo}&&&\hphantom {L3ooo}&\hphantom {R3oooooooooooooooo}&&&&\hphantom {R5oooooooooooooooooooooo}\nonumber \end {align*}
Der Entladevorgang einer Induktivität \(L\) über einen Widerstand \(R\) ist ähnlich zum Ladevorgang über einen Widerstand \(R\) mit Gleichspannung \(U_q\). Der Kurzschluss über \(R\) entspricht einer Spannungsquelle mit \(U_q=0\ \mathrm {V}\). Entladevorgang und Ladevorgang unterscheiden sich lediglich in den Anfangsbedingungen und dem Störterm der jeweiligen DGL. Die Zeitkonstante \(\tau \) ist identisch für den Lade- und Entladevorgang. Auf eine detaillierte Berechnung wird daher an dieser Stelle verzichtet.
Abbildung 2 zeigt das Schaltbild (a) und den Spannungs- und Stromverlauf (b) der Induktivität \(L\) beim Entladen über einen Widerstand \(R\) ab Schaltzeitpunkt \(t=0\). Die Induktivität ist vor dem Schalten in Reihe mit dem Widerstand \(R\) an eine Gleichspannungsquelle \(U_q\) angeschlossen. Zum Schaltzeitpunkt ist die Induktivität vollständig geladen(stationärer Zustand) und führt vor dem Schalten den Konstantstrom \(U_q/R\).
Reale Induktivitäten lassen sich durch eine Reihenschaltung aus einer idealen Induktivität \(L\) und einem ohmschen Widerstand \(R_{\text {Cu}}\) modellieren, der den Kupferverlusten entspricht. Durch Parallelschaltung eines ohmschen Widerstandes \(R_{\text {Fe}}\) unmittelbar zur Induktivität \(L\) lassen sich zudem Eisenverluste modellieren.
Abbildung 3 zeigt das Schaltbild (a) einer realen Spule mit Induktivität \(L\) in Serie zu einem Widerstand \(R_{\text {Cu}}\) (hier \(R_1\)). Unmittelbar parallel zur Induktivität befindet sich der ohmsche Widerstand \(R_{\text {Fe}}\) (entspricht \(R_2\)). Die Induktivität wird ab \(t=0\) über eine ideale Konstantspannungsquelle \(U_q\) geladen und ist vorher vollständig entladen. Daneben abgebildet sind die zugehörigen den Spannungs- und Stromverläufe (b).
Im Vergleich zum Ladevorgang eines reine RL-Serienschaltung in Beispiel ?? springt die Spannung über der Induktivität nicht auf die ganze Quellenspannung sondern auf einen geringeren Wert begrenzt durch den Spannungsteiler \(\frac {R_2}{R_1+R_2}\). Der Eingangsstrom macht bedingt durch die Eisenverluste einen Sprung zum Schaltzeitpunkt und nähert sich dann exponentiell dem Strom \(\frac {U_q}{R_1}\). Der Strom durch \(R_2\) springt beim Schalten auf den Wert \(\frac {U_q}{R_1+R_2}\) und fällt dann exponentiell ab. Der Strom durch die Induktivität nähert sich exponentiell dem Strom \(\frac {U_q}{R_1}\) an. Die Zeitkonstante beträgt \(\tau =\frac {L}{R_1||R_2}\).
Die Vorgehensweise zur Berechnung von Schaltvorgängen bei sinusförmiger Anregung ist prinzipiell gleich zur Vorgehensweise bei gleichförmiger Anregung. Deshalb wird in diesem Kapitel nur auf die Besonderheiten bei sinusförmiger Anregung eingegangen und die Berechnung anhand eines Beispiels erläutert.
Die Differentialgleichungen bei Schaltungen mit Wechselspannungs- oder stromquellen unterscheiden sich gegenüber den Gleichspannungs- oder -stromfällen lediglich durch die rechte Seite der DGL, dem Störterm. Der Störterm ergibt sich aus der Anregung und ist bei sinusförmiger Anregung linearer, zeitinvarianter Systeme ebenfalls sinusförmig.
Aufgrund der Zeitabhängigkeit sinusförmiger Anregungen, ist der exakte Schaltzeitpunkt entscheiden für das Verhalten des Systems. Präziser formuliert ist die Phasenlage der Anregung zum Schaltzeitpunkt entscheidend.
Am Beispiel eines RC-Gliedes wird in Kapitel 2.1 die Berechnung des Schaltvorgangs bei sinusförmiger Anregung gezeigt. Dabei wird die Abhängigkeit des Schaltvorgangs vom Schaltzeitpunkt und die Möglichkeit transienter Spitzenströme und -spannungen näher erläutert.
Exemplarisch ist in Beispiel ?? die Berechnung eines Schaltvorganges für ein RL-Glied bei Anregung mit Wechselspannung zusammenfassend präsentiert.
Zur Erläuterung der Besonderheiten von Schaltvorgängen bei sinusförmiger Anregung wird das Beispiel eines RC-Gliedes betrachtet. Die Berechnung erfolgt wie in Beispiel ?? nach Merksatz ??.
Eine Kapazität \(C\) wird über einen Widerstand \(R\) ab dem Schaltzeitpunkt \(t=t_0\) an eine ideale Wechselspannungsquelle mit Spannung \(u_q(t) = \hat {U}_q \cdot \cos (\omega t + \varphi _q)\) angeschlossen. Die Kapazität \(C\) ist zu Beginn vollständig entladen. Abbildung 4 zeigt das Schaltbild dieser Anordnung.
1.) Differentialgleichung aufstellen:
Die inhomogene DGL von \(u_C\) für \(t \geq t_0\) ergibt sich analog zu Beispiel ?? zu: \begin {align} RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C(t) + u_C(t) ={}& u_q(t) \\ \text {mit} &u_q(t) = \hat {U_q} \cdot \cos (\omega t + \varphi _q) \end {align}
Gegenüber Beispiel ?? ist lediglich der Störterm verändert. Der Gleichspannungsterm \(U_q\) ist hier durch den Wechselspannungsterm \(u_q\) ersetzt.
2.) Homogene Lösung, allgemein (flüchtiger Zustand):
Die homogene Lösung \(u_{C,h}\) ist unabhängig vom Störterm und damit von der Anregung. Die Lösung ist aus Beispiel ?? übernommen mit Berücksichtigung des variablen Schaltzeitpunktes \(t_0\): \begin {align} u_{C,\mathrm {h}} &= K \cdot \mathrm {e}^{-\frac {t'}{\tau }} \qquad \text {mit} t' = t-t_0 \nonumber \\ &= K \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} \qquad \text {mit} \tau = RC \label {eq:rc:charge:ac:homogeneloesung} \end {align}
Da der Exponentialansatz erst ab Schaltzeitpunkt \(t_0\) gilt, wird dieser von der Zeit \(t\) subtrahiert.
3.) Partikuläre Lösung (eingeschwungener Zustand):
Die partikuläre Lösung \(u_{C,p}\) entspricht bei sinusförmiger Anregung ebenfalls einer sinusförmigen Größe mit gleicher Frequenz wie die Anregung wie in in Kapitel ?? beschrieben ist. Der eingeschwungene Zustand lässt sich mittels komplexem Amplitudenzeiger \(\hat {\underline {U}}_{C,p}\) wie folgt beschreiben: \begin {align} u_{C,p} &= \hat {U_{C,p}} \cdot \cos (\omega t + \varphi _{C,\mathrm {p}}) \label {eq:rc:charge:ac:partikulaereloesung}\\ &= \Re {\left \{ \hat {\underline {U}_{C,p}} \cdot \mathrm {e}^{\mathrm {j} \omega t} \right \}} \qquad \text {mit} \hat {\underline {U}_{C,p}} = \hat {U_{C,p}} \cdot \mathrm {e}^{\mathrm {j} \varphi _{C,\mathrm {p}}} \end {align}
Die Amplitude \(\hat {U}_{C,p}\) und der (Last-)Phasenwinkel \(\varphi _{C,\mathrm {p}}\) lassen sich gemäß komplexen Spannungsteiler bestimmen. \begin {align} \hat {\underline {U}_{C,p}} &= \hat {\underline {U}_q} \cdot \frac {\underline {Z}_C}{R + \underline {Z}_C} = \hat {\underline {U}_q} \cdot \frac {\frac {1}{\mathrm {j}\omega C}}{R + \frac {1}{\mathrm {j} \omega C}} \nonumber \\ &= \frac {\hat {\underline {U}_q}}{1 + \mathrm {j} \omega R C} \qquad \text {mit} \hat {\underline {U}_q} = \hat {U_q} \cdot \mathrm {e}^{\mathrm {j} \varphi _q} \label {eq:rc:charge:ac:komplex} \end {align}
Für die Amplitude \(\hat {U}_{C,p}\) und die Phase \(\varphi _{C,\mathrm {p}}\) folgt aus Gl. ??: \begin {align} \hat {U_{C,p}} = \frac {\hat {U_q}}{\sqrt {1 + \left (\omega RC\right )^2}} \qquad \text {und}\qquad \varphi _{C,\mathrm {p}} = \varphi _q - \arctan \left (\omega RC\right ) \label {rc:charge:ac:amplitudephase} \end {align}
4.) Inhomogene Lösung, allgemein (Überlagerung):
Aus der Überlagerung von Gl. ?? und ?? folgt die allgemeine Lösung der inhomogenen DGL: \begin {align} u_C &= u_{C,\mathrm {h}} + u_{C,p} \nonumber \\ &= K \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} + \hat {U_{C,p}} \cdot \cos (\omega t + \varphi _{C,\mathrm {p}}) \label {eq:rc:charge:ac:allg} \end {align}
5.) Konstanten bestimmen (Anfangsbedingung):
Aus der Anfangsbedingung, dass die Kapazität zu Beginn entladen ist, folgt für die Konstante \(K\): \begin {align} u_C(t_0) &\overset {!}{=} 0 \nonumber \\ K \cdot \cancel {\mathrm {e}^{0}} + \hat {U_{C,p}} \cdot \cos (\omega t_0 + \varphi _{C,\mathrm {p}}) &= 0 \nonumber \\ K &= -\hat {U_{C,p}} \cdot \cos (\omega t_0 + \varphi _{C,\mathrm {p}}) \label {eq:rc:charge:ac:k} \end {align}
Mit Gl. ?? eingesetzt in ?? ergibt sich die eindeutige Lösung für \(u_C(t)\): \begin {align} u_C(t) &= \underbrace {-\hat {U_{C,p}} \cdot \cos (\omega t_0 + \varphi _{C,\mathrm {p}}) \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }}}_{u_{C,\mathrm {h}}} + \underbrace {\hat {U_{C,p}} \cdot \cos \left (\omega t + \varphi _{C,\mathrm {p}}\right )}_{u_{C,p}} \label {eq:rc:charge:ac:uc} \end {align}
An Gleichung ?? ist erkennbar, dass der flüchtige Zustand \(u_{C,f}=u_{C,h}\) ab \(t_0\) exponentiell gegen null strebt. Im Gegensatz zum DC-Fall (Beispiel ??) ist der Startwert der Exponentialkurve \(K\) aus Gleichung ?? abhängig von \(t_0\), da der eingeschwungene Zustand \(u_{C,e}=u_{C,p}\) zeitabhängig ist.
Verhalten bei Variation des Schaltzeitpunktes/der Zeitkonstante:
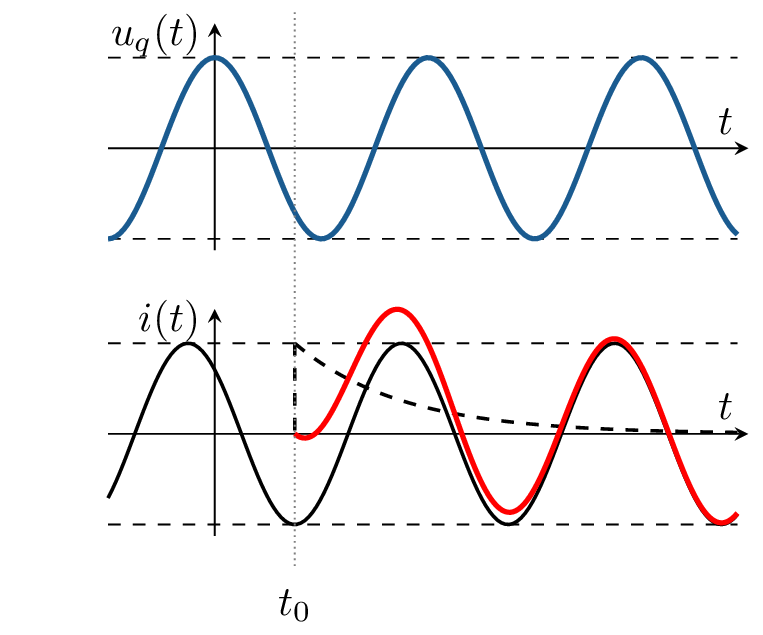
Abbildung 4a zeigt den Spannungsverlauf der Anregung \(u_q\) bei einem Nullphasenwinkel \(\varphi _q\) von Null und den Spannungsverlauf der Kapazität \(u_C\). Zum Vergleich ist \(u_C\) für zwei verschiedenen Schaltzeitpunkten \(t_0\) gezeigt. Das ist einmal beim negativen Scheitelwert und einmal beim Nulldurchgang von \(u_{C,p}\). \(u_C\) ist als Überlagerung des flüchtigen Zustandes \(u_{C,h}\) (schwarz, gestrichelt) und des eingeschwungenen Zustandes \(u_{C,p}\) (schwarz) dargestellt.
Wie zu erkennen ist, ist der Ausgleichsvorgang maximal (\(|K|=max.\)), wenn die Differenz \(|u_{C,p}(t_0)- u_C(t_0)|\) maximal ist. Erfüllt die \(u_{C,p}\) bereits die Anfangsbedingung mit \(u_{C,p}(t_0)\overset {!}{=}u_C(t_0)\), entfällt der flüchtige Zustand vollständig \(K=0 \Rightarrow u_{C,h}=0\) und es kommt zu keinem Ausgleichsvorgang.
In Abbildung 4b wird der Spannungsverlauf \(u_C\) für verschiedenen Zeitkonstanten \(\tau \) gezeigt. Einmal beträgt \(\tau =\frac {2\pi }{\omega }\), einmal \(\tau =\frac {20\pi }{\omega }\). In beiden Fällen ist \(t_0\) so gewählt, dass der Ausgleichsvorgang maximal wird.
Bei großen Zeitkonstanten klingt der flüchtige Zustand langsamer ab, dadurch kann es bei ungünstigen Schaltzeitpunkten zu Überspannungen/-strömen kommen. Ist \(u_C\) wie im Beispiel nach Anfangsbedingung zu Beginn entladen (\(u_C(t_0)=0\)), kann \(u_C\) bis zum doppelten Scheitelwert von \(u_{C,p}\) ansteigen. Ist \(u_C\) hingegen zu Beginnn bereits bis zum negativen/positiven Scheitelwert von \(u_{C,p}\) geladen, kann \(u_C\) sogar bis zum dreifachen Scheitelwert von \(u_{C,p}\) ansteigen.
Merke: Ausgleichsvorgänge bei AC-Anregung
Durch geschicktes Schalten können Ausgleichsvorgänge bei AC-Anregung vermieden werden.
Bei großen Zeitkonstanten sind Überwerte bis zum doppelten/dreifachen Scheitelwert möglich.
Beispiel ?? zeigt exemplarisch die Berechnung eines Schaltvorgangs für ein RL-Glied bei Anregung mit Wechselspannung nach Merksatz ??.
Die Berechnung von Schaltvorgängen bei sinusförmiger Anregung für Induktivitäten erfolgt analog zu der Berechnung für Kapazitäten in Kapitel 2.1. Es gelten die gleichen Besonderheiten bezüglich Schaltzeitpunkten und möglicher transienter Spitzenströme und -spannungen wie bei Kapazitäten.
Im Beispiel ist die DGL der partikulären Lösung nach Gleichung ?? transformiert: \begin {align*} &\text {DGL$_{\mathrm p}$:}& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} i_{\mathrm p} + i_{\mathrm p} &= \frac {u_q}{R} & &\text {mit} u_q = \Re \left \{\underline {\hat {U}_q}\cdot \mathrm {e}^{\mathrm {j}\omega t}\right \} \vphantom {\Bigg |}\\ &\text {transformiert:}& \Leftrightarrow \frac {L}{R} \cdot \mathrm {j}\omega \, \underline {\hat {I}_{\mathrm p}} + \underline {\hat {I}_{\mathrm p}} &= \frac {\underline {\hat {U}_q}}{R} & &\text {mit} \underline {\hat {U}_q} = \hat {U_q}\cdot \mathrm {e}^{\mathrm {j}\varphi _q} \vphantom {\Bigg |} \end {align*}
Der Ansatz bietet eine einfache Umstellung nach dem komplexen Amplitudenzeiger der partikulären Lösung und ist prinzipiell gleichwertig mit der Herleitung über komplexe Spannungsteiler wie sie in Gleichung ?? am Beispiel des RC-Gliedes gezeigt ist.
Beispiel 5: RL-Glied, Schaltvorgang mit Wechselspannungsquelle
Bestimmung des Strom \(i\) durch die Induktivität \(L\) in Reihe mit dem ohmschen Widerstand \(R\) bei Zuschalten der idealen Wechselspannungsquelle \(u_q = \hat {U_q} \cdot \cos (\omega t + \varphi _q)\) ab Schaltzeitpunkt \(t=t_0\). Zuvor fließt kein Strom.
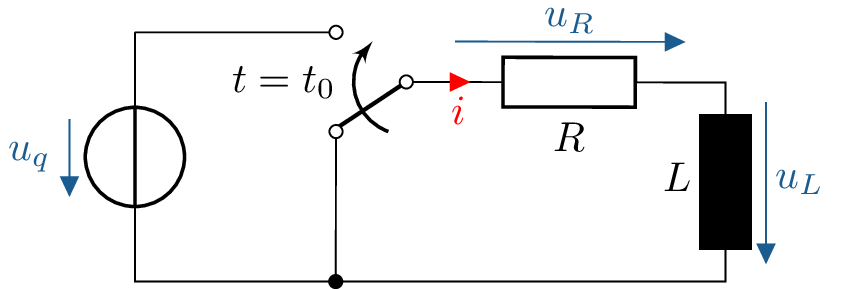 \begin {equation*} \begin {aligned} \text {gegeben:}&& &i(t_0),\ u_q,\ R,\ L \\ \text {gesucht:}&& &i(t),\ u_L(t) \end {aligned} \end {equation*}
\begin {equation*} \begin {aligned} \text {gegeben:}&& &i(t_0),\ u_q,\ R,\ L \\ \text {gesucht:}&& &i(t),\ u_L(t) \end {aligned} \end {equation*}
1.) DGL aufstellen: von \(i\) für \(t \geq t_0\), Lösung aus Bsp. ?? \begin {align*} &\text {DGL}:&&& \frac {L}{R} \cdot \frac {\mathrm {d}}{\mathrm {d}t} i + i &= \frac {u_q}{R}&&& &\text {mit} u_q = \hat {U_q} \cdot \cos (\omega t + \varphi _q) \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5ooooooooooooooooooooooo}\nonumber \end {align*}
2.) Homogene Lösung, allg.: (flüchtig), Lösung aus Bsp. ?? für Schaltzeitpunkt \(t_0\) \begin {align*} &\text {hom. Lsg.:} &&& i_{\mathrm {h}}&= K \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} &&& &\text {mit} \tau = \frac {L}{R} \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5ooooooooooooooooooooooo}\nonumber \end {align*}
3.) Partikulare Lösung: (eingeschwungen) mit \(t \to \infty \), kompl. Wechselstromrechnung\begin {align*} &\text {transf.}:&&& \frac {L}{R} \cdot \mathrm {j}\omega \, \underline {\hat {I}_{\mathrm p}} + \underline {\hat {I}_{\mathrm p}} &= \frac {\underline {\hat {U}_q}}{R} &&& &\text {mit} \underline {\hat {U}_q}=\hat {U_q} \cdot \mathrm {e}^{\mathrm {j}\varphi _q}\\ &\text {Zeiger:}&&& \underline {\hat {I}_{\mathrm p}} &= \frac {\underline {\hat {U}_q}}{R} \cdot \frac {1}{1 + \mathrm {j} \omega \frac {L}{R}} &&& &\text {mit} \underline {\hat {I}_{\mathrm p}} = \hat {I_{\mathrm p}}\cdot \mathrm {e}^{\mathrm {j}\varphi _I}\\ &&&& \hat {I_{\mathrm p}} &= \frac {\hat {U_q}/R}{\sqrt {1 + \left (\omega \frac {L}{R}\right )^2}} &&& & \varphi _I = \varphi _q - \arctan \left (\omega \frac {L}{R}\right ) \\ &\text {part. Lsg.}:&&& i_{\mathrm p} &= \hat {I_{\mathrm p}} \cdot \cos (\omega t + \varphi _I) &&& &\text {mit} i_{\mathrm p} = \Re \left \{\underline {\hat {I}_{\mathrm p}} \cdot \mathrm {e}^{\mathrm {j}\omega t}\right \} \vphantom {\Bigg |} \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3ooooooooooo}&\hphantom {R3ooooooooooooooo}&&&&\hphantom {R5ooooooooooooooooooooooo}\nonumber \end {align*}
4.) Inhomogene Lösung, allg.: (Überlagerung)\begin {align*} &\text {allg. Lsg.:}&&& i &= \underbrace { \vphantom {\big |} K \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} }_{i_{\mathrm h}} + \underbrace { \vphantom {\big |} \hat {I_{\mathrm p}} \cdot \cos (\omega t + \varphi _I) }_{i_{\mathrm p}}&&& \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3oooooo}&\hphantom {R3ooooooooooooooooooooooooooooooooooooooooooo}&&&&\hphantom {R5}\nonumber \end {align*}
5.) Konstanten bestimmen: (AB einsetzen)\begin {align*} &\text {Anfangsbed.:}&&& i(t_0) &= K \cdot \cancel {\mathrm {e}^0} + \hat {I_{\mathrm p}} \cdot \cos (\omega t_0 + \varphi _I) \overset {!}{=} 0 \\ &&&& \Rightarrow K &= -\hat {I_{\mathrm p}} \cdot \cos (\omega t_0 + \varphi _I) \\ &\text {eindeut. Lsg.:}&&& i(t) &= -\hat {I_{\mathrm p}} \cdot \cos (\omega t_0 + \varphi _I) \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} + \hat {I_{\mathrm p}} \cdot \cos (\omega t + \varphi _I) \\[-15pt]&\hphantom {R1oooooooooo}&&&\hphantom {L3oooooo}&\hphantom {R3ooooooooooooooooooooooooooooooooooooooooooo}&&&&\hphantom {R5}\nonumber \end {align*}
Spannung \(u_L\) über der Induktivität \(L\) über \(u_L = L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i\) berechnen. \begin {align*} &\text {Spannung:}&&& u_L(t) &= R \cdot \hat {I_{\mathrm p}} \cdot \cos (\omega t_0 + \varphi _I) \cdot \mathrm {e}^{-\frac {t-t_0}{\tau }} - \omega L \cdot \hat {I_{\mathrm p}} \cdot \sin (\omega t + \varphi _I) \end {align*}
Systeme mit zwei unterschiedlichen Energiespeichern (Induktivität \(L\) und Kapazität \(C\)) sind prinzipiell schwingungsfähig. Daher werden RLC-Glieder auch als Schwingkreise oder Resonanzkreise bezeichnet. Die Schwingungsfähigkeit lässt sich anhand der Eigenwerte bestimmen und beschreiben. Ein anderer Ansatz ist die Betrachtung der (Schwingkreis-)Güte \(Q\). [Vgl. Modul 8]
Abbildung 6 zeigt das Schaltbild eines RLC-Gliedes beim Laden mit konstanter Gleichspannung \(U_q\). Daneben sind die Zeitverläufe der Kondensatorspannung für die drei möglichen Fälle dargestellt. Das sind der aperiodischen Fall, der aperiodischen Grenzfall und der periodischen Fall die in Kapitel 3.1 näher beschrieben sind.
Die Berechnung von Schaltvorgängen bei RLC-Gliedern erfolgt analog zu den Beispielen für RC- und RL-Glieder aus den vorigen Kapiteln.
1.) DGL aufstellen: für \(u_C\) für \(t \geq 0\) \begin {align} u_L + u_R +u_C &= u \nonumber \\ L \cdot \frac {\mathrm {d}}{\mathrm {d}t} i + R \cdot i + u_C&= U_q \nonumber \\ LC \cdot \frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} u_C + RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_C + u_C &= U_q \label {eq:dgl:rlc:dc} \end {align}
Aufgrund der zwei verschiedenen Energiespeichern ergibt sich eine DGL 2. Ordnung.
2.) Homogene Lösung, allg.: (flüchtig) (ohne Störterm)
Die Form der homogenen Lösung ist abhängig von der Art der Eigenwerte. \begin {align} &\text {hom. DGL:}& LC \cdot \frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}} u_{C,\mathrm {h}} + RC \cdot \frac {\mathrm {d}}{\mathrm {d}t} u_{C,\mathrm {h}} + u_{C,\mathrm {h}} &= 0 &&\text {mit} u_{C,\mathrm {h}} = K \cdot \mathrm {e}^{\lambda t} \label {eq:dgl:rlc:homo}\\[6pt] &\text {char. Polynom:}& \lambda ^2 + \frac {R}{L} \cdot \lambda + \frac {1}{LC} &= 0 \nonumber \\[6pt] &\text {Eigenwerte:}& \lambda _{1/2} = -\frac {R}{2L} \pm \sqrt {\left (\frac {R}{2L}\right )^2 - \frac {1}{LC}}& &&\text {mit} D = \left (\frac {R}{2L}\right )^2 - \frac {1}{LC} \label {eq:dgl:rlc:lambda} \end {align}
Durch Anwenden der \(p\)-\(q\)-Formel (Mitternachtsformel) ergeben sich für die Eigenwerte (EW) \(\lambda _{1/2}\) je nach Wurzelterm entweder zwei unterschiedliche oder zwei identische Werte. Die homogenen Lösung nimmt daher, wie in Kapitel ?? beschrieben ist, eine der folgenden zwei Formen an: \begin {equation} \text {hom. Lsg.:}\qquad \qquad \qquad u_{C,\mathrm {h}} = \begin {cases} K_1 \cdot \mathrm {e}^{\lambda _1 t} + K_2 \cdot \mathrm {e}^{\lambda _2 t} & \text {für}\lambda _1 \neq \lambda _2 \\ (K_1 + K_2 \cdot t) \cdot \mathrm {e}^{\lambda t} & \text {für}\lambda _1 = \lambda _2 = \lambda \end {cases} \qquad \qquad \qquad \label {eq:dgl:rlc:homolsg:cases} \end {equation} Die Fallunterscheidung kann anhand der sogenannten Diskriminante \(D\) vorgenommen werden.
Die Diskriminante \(D\) ist der Term unter der Wurzel in Gleichung ?? zur Bestimmung von \(\lambda _{1/2}\). \begin {align} &&\lambda _{1/2} &= -\frac {R}{2L} \pm \sqrt {\smash {\underbrace {\left (\frac {R}{2L}\right )^2 - \frac {1}{LC}}_{{\text {Diskriminante }D}}}\vphantom {\left (\frac {R}{L}\right )^2} }\label {eq:dgl:rlc:lambda:allg}\\[-10pt]\nonumber \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align}
Tabelle 2 listet alle drei Fälle mit Art der Eigenwerte und relative Aussagen bezüglich der Dämpfung des Schwingkreises. Als Unterscheidungsmerkmal sind die Wertebereiche der Diskriminante \(D\) respektive der Schwingkreisgüte \(Q_S\) (Vgl. Modul 8) mit angegeben.
| Fallunterscheidung | Dämpfung | Diskrimi. | Güte | Eigenwerte \(\lambda _{1/2}\) |
| aperiodischer Fall | stark | \(D > 0\) | \(Q_S < 0,5\) | Zwei verschiedene, reelle EW |
| aperiodischer Grenzfall | kritisch | \(D = 0\) | \(Q_S = 0,5\) | Eine doppelte, reelle EW |
| periodischer Fall | schwach | \(D < 0\) | \(Q_S > 0,5\) | konjugierte, komplexe EW |
Ein Ortskurvendiagramm der Eigenwerte wird im optionalen Exkurs in Kapitel 4.2 gezeigt. Der Zusammenhang zwischen \(\lambda \) und \(Q_S\) wird im optionalen Exkurs in Kapitel 4.3 näher erläutert.
Ist die Diskriminante \(D\) positiv, ist der Wurzelterm reellwertig und immer kleiner als der Betrag des Terms \(\frac {R}{2L}\) vor der Wurzel. Dadurch sind beide Eigenwerte verschieden, reell und negativ.\begin {align*} &\text {für} D > 0 \text {gilt}& &\phantom {\mathrel {\phantom {=}}-}\frac {R}{2L} \overset {!}{>} \sqrt {\left (\frac {R}{2L}\right )^2 - \frac {1}{LC}} &&\Rightarrow \text {2 reelle EW} \\[-10pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align*}
2.) Homogene Lösung: (flüchtig) \begin {align} && u_{C,\mathrm {h}} &= K_1 \cdot \mathrm {e}^{\lambda _1 t} + K_2 \cdot \mathrm {e}^{\lambda _2 t} &&\text {mit} \lambda _1 \neq \lambda _2,\ \lambda < 0 \label {eq:dgl:rlc:homolsg:aperiodisch} \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align}
Die Konstanten \(K_1\) und \(K_2\) müssen beide reell sein, damit die Lösung reellwertig bleibt. Der flüchtige Zustand entspricht damit der Addition zweier Exponentialfunktionen. Dabei dominiert die langsamer Exponentialfunktion, das heißt die mit der größeren Zeitkonstante (Vgl. Exkurs in Kapitel 4.2).
3.) Partikuläre Lösung: (eingeschwungen, identisch für alle drei Fälle)\begin {align*} && u_{C,\mathrm {p}} &= U_q \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align*}
4.) Allgemeine Lösung: (Überlagerung)\begin {align} && u_C(t) &= K_1 \cdot \mathrm {e}^{\lambda _1 t} + K_2 \cdot \mathrm {e}^{\lambda _2 t} + U_q \nonumber \\[-14pt] &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo} \nonumber \end {align}
5.) Konstanten bestimmen: (wie bekannt)
Sei \(u_C(0)=0\) und \(i(0)=0 \Rightarrow \frac {\mathrm {d}}{\mathrm {d}t}\, u_C(0) = 0 \) als Anfangsbedingungen (AB) gegeben, so folgt:
\begin {align*} &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo}\\[-15pt] &\text {1. AB:}& u_C(0) &= K_1 \cdot \cancel {\mathrm {e}^{\lambda _1 0}} + K_2 \cdot \cancel {\mathrm {e}^{\lambda _2 0}} + U_q \overset {!}{=} 0 & \Rightarrow K_1 &= -K_2 -U_q\\ &\text {2. AB:}& \frac {\mathrm {d}}{\mathrm {d}t} u_C(0) &= K_1 \cdot \lambda _1 \cdot \cancel {\mathrm {e}^{\lambda _1 0}} + K_2 \cdot \lambda _2 \cdot \cancel {\mathrm {e}^{\lambda _2 0}} + \cancel {0} \overset {!}{=} 0 & \Rightarrow K_1 &= - K_2 \frac {\lambda _2}{\lambda _1} \nonumber \\ &\Longrightarrow & K_1 &= \frac {U_q}{\frac {\lambda _1}{\lambda _2}-1} \text {und} K_2 = \frac {U_q}{\frac {\lambda _2}{\lambda _1}-1} \end {align*}
Ist die Diskriminante \(D\) exakt null, sind beide Eigenwerte identisch, reell und negativ. Durch die doppelte Nullstelle ergibt sich eine spezielle Form der homogenen Lösung durch Überlagerung der zwei Ansätze (\(K_1 \cdot \mathrm {e}^{\lambda _1 t}\) und \(K_2 \cdot t \cdot \mathrm {e}^{\lambda _2 t}\)).\begin {align*} \vphantom {\sqrt {\left (\frac {R}{2L}\right )^2}} &\text {für} D = 0 \text {gilt}& \lambda _{1/2} &= -\frac {R}{2L} \cancel { {} \pm {} \sqrt {0}} = \lambda &&\Rightarrow \text {1 reeller EW} \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align*}
2.) Homogene Lösung: (flüchtig) \begin {align} && u_{C,\mathrm {h}} &= \left ( K_1 + K_2 \cdot t \right ) \cdot \mathrm {e}^{\lambda t} &&\text {mit} \lambda _1 = \lambda _2 < 0 \label {eq:dgl:rlc:homolsg:grenzfall} \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align}
3.) Partikuläre Lösung: (eingeschwungen)\begin {align*} && u_{C,\mathrm {p}} &= U_q \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align*}
4.) Allgemeine Lösung: (Überlagerung)\begin {align} && u_C(t) &= \left ( K_1 + K_2 \cdot t \right ) \cdot \mathrm {e}^{\lambda t} + U_q \nonumber \\[-14pt] &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo} \nonumber \end {align}
5.) Konstanten bestimmen: (wie bekannt)
Sei \(u_C(0)=0\) und \(i(0)=0 \Rightarrow \frac {\mathrm {d}}{\mathrm {d}t}\, u_C(0) = 0 \) als Anfangsbedingungen (AB) gegeben, so folgt:
\begin {align*} &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo}\\[-15pt] &\text {1. AB:}& u_C(0) &= \left ( K_1 + \cancel {K_2 \cdot 0 }\right ) \cancel {\cdot \mathrm {e}^{\lambda 0}} + U_q \overset {!}{=} 0 & \Rightarrow K_1 &= -U_q\\ &\text {2. AB:}& \frac {\mathrm {d}}{\mathrm {d}t} u_C(0) &= \left ( K_1 + \cancel {K_2 \cdot 0} \right ) \cdot \lambda \cdot \cancel {\mathrm {e}^{\lambda 0}} + K_2 \cdot \cancel {\mathrm {e}^{\lambda 0}} \overset {!}{=} 0 & \Rightarrow K_2 &= -K_1 \cdot \lambda \nonumber \\ &\Longrightarrow & K_1 &= -U_q \text {und} K_2 = +U_q \cdot \lambda \end {align*}
Ist die Diskriminante negativ, gibt es zwei komplex konjugierte Eigenwerte mit negativem Realteil. Umformung mit \(\sqrt {-1}=\mathrm {j}\cdot \sqrt {1}\) und Herleitung für \(u_{C,h}\) in Kapitel 4.1:\begin {align} &\text {für} D < 0 \text {gilt}& \lambda _{1/2} &= -\underbrace { \vphantom {\sqrt {\left (\frac {R}{2L}\right )^2}} \frac {R}{2L} }_{\mathrm{d}elta } \pm \, \mathrm {j} \cdot \underbrace { \sqrt {\frac {1}{LC} - \left (\frac {R}{2L}\right )^2} }_{\omega _d} &&\Rightarrow \text {2 kompl. EW} \label {eq:dgl:rlc:lambda:periodisch} \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align}
2.) Homogene Lösung: (flüchtig) \begin {align} && u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot C_0 \cdot \sin (\omega _d t + \varphi _0) &&\text {mit} \lambda _{1/2} = -\mathrm{d}elta \pm \mathrm {j}\,\omega _d \label {eq:dgl:rlc:homolsg:periodisch} \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align}
Die homogene Lösung entspricht einer abklingenden Schwingung mit der Abklingkonstante \(\mathrm{d}elta \) (neg. Realteil der EW) und der gedämpften Eigenkreisfrequenz \(\omega _d\) (pos. Imaginärteil der EW). Eine Herleitung für Gl. ?? aus Gl. ?? erfolgt in Kapitel 4.1.
3.) Partikuläre Lösung: (eingeschwungen)\begin {align*} && u_{C,\mathrm {p}} &= U_q \\[-15pt] &\hphantom {1rrrrrrrrrrrrrrrr} & \hphantom {2llllll}&\hphantom {\mathrel {\phantom {=}}2rrrrrrrrrrrrrrrrrrrrrrrrrrr} &&\hphantom {3rrrrrrrrrrrrrrrrrrrrrrrr} \nonumber \end {align*}
4.) Allgemeine Lösung: (Überlagerung)\begin {align} && u_C(t) &= \mathrm {e}^{-\mathrm{d}elta t} \cdot C_0 \cdot \sin (\omega _d t + \varphi _0) + U_q \nonumber \\[-14pt] &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo} \nonumber \end {align}
5.) Konstanten bestimmen: (wie bekannt) \begin {align*} &\hphantom {1Rooooooo}&\hphantom {2Loooooo}&\hphantom {2Roooooooooooooooooooooooooooooooooo}&\hphantom {3Loooooo}&\hphantom {3Roooooooooo}\\[-15pt] &\text {1. AB:}& u_C(0) &= \cancel {\mathrm {e}^{-\mathrm{d}elta 0}} \cdot C_0 \cdot \sin (\cancel {\omega _d t } + \varphi _0) + U_q \overset {!}{=} 0\\ &\text {2. AB:}& \frac {\mathrm {d}}{\mathrm {d}t} u_C(0) &= -\mathrm{d}elta \cdot \cancel {\mathrm {e}^{-\mathrm{d}elta 0}} \cdot C_0 \cdot \sin (\varphi _0) + {\cancel {\mathrm {e}^{-\mathrm{d}elta 0}} \cdot C_0 \cdot \omega _d \cdot \cos (\varphi _0) \overset {!}{=} 0 }\nonumber \\ &\Longrightarrow & C_0 &= -\frac {U_q}{\sin (\varphi _0)} \text {und} \varphi _0 = \arctan \left (\frac {\omega _d}{\mathrm{d}elta }\right ) \end {align*}
In Abbildung 7 ist der zeitlichen Verlauf der Spannung \(u_C(t)\) für \(t=0\) bis \(t=5\cdot \frac {1}{\mathrm{d}elta }\) gezeigt. In der gewählten Skalierung beträgt \(\omega _0\) das vierfache der Abklingkonstante \(\mathrm{d}elta \) (Güte \(Q_S = 2\)).
In diesem Kapitel sind ergänzende Exkurse zum Verhalten von Schwingkreisen enthalten, die zur Vertiefung des Themas dienen und Brücken zu weiteren Themengebieten schlagen. Die Inhalte der Exkurse sind für das Verständnis der restlichen Modulinhalte nicht zwingend erforderlich und können bei Bedarf übersprungen werden.
Aus der allgemeinen homog. Lösung im periodischen Fall (Gl. 5) folgt mit \(\lambda _{1/2}\) (Gl. ??): \begin {align*} u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot \left ( K_1 \cdot \mathrm {e}^{+\mathrm {j}\omega _d t} + K_2 \cdot \mathrm {e}^{-\mathrm {j}\omega _d t} \right ) \end {align*}
\(K_1\) und \(K_2\) müssen komplex konjugiert sein, damit \(u_{C,\mathrm {h}}\) reell ist! [?, Vgl. S. 379] \begin {align} &\text {mit}& K_1 &= a + \mathrm {j} b {\text {und} K_2 = a - \mathrm {j} b\text {mit} a,b \in \mathbb {R}} \nonumber \\[6pt] && u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot \left [ (a + \mathrm {j} b) \cdot \mathrm {e}^{+\mathrm {j}\omega _d t} + (a - \mathrm {j} b) \cdot \mathrm {e}^{-\mathrm {j}\omega _d t} \right ] \nonumber \\[2pt] && u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot \left [\vphantom {\Big |} \smash { a \cdot \underbrace {\left ( \mathrm {e}^{+\mathrm {j}\omega _d t} + \mathrm {e}^{-\mathrm {j}\omega _d t} \right )}_{2\cos (\omega _d t)} + \mathrm {j} b \cdot \underbrace {\left ( \mathrm {e}^{+\mathrm {j}\omega _d t} - \mathrm {e}^{-\mathrm {j}\omega _d t} \right )}_{2\mathrm {j}\sin (\omega _d t)} }\right ] \nonumber \\[20pt] &\text {mit}& \mathrm {e}^{+\mathrm {j}x} + \mathrm {e}^{-\mathrm {j}x} &= \cos (x) + \cancel {\mathrm {j}\sin (x)} + \cos (x) - \cancel {\mathrm {j}\sin (x)} = 2\cos (x) \nonumber \\ && \mathrm {e}^{+\mathrm {j}x} - \mathrm {e}^{-\mathrm {j}x} &= \cancel {\cos (x)} + \mathrm {j}\sin (x) - \cancel {\cos (x)} + \mathrm {j}\sin (x) = 2\mathrm {j}\sin (x) \nonumber \\[6pt] && u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot \left [\vphantom {\Big |}\smash { \underbrace {2a}_{C_1} \cdot \cos (\omega _d t) - \underbrace {2b}_{C_2} \cdot \sin (\omega _d t) }\right ] \label {eq:dgl:rlc:homolsg:periodisch:herleitung} \end {align}
Die homogene Lösung entspricht im periodischen Fall einer abklingenden (\(\mathrm {e}^{-\mathrm{d}elta t}\)) Überlagerung der Schwingungen \(z_1\) und \(-z_2\) mit gleicher Kreisfrequenz \(\omega _d\) und Phasenverschiebung von \(1/{\pi }{2}\) zueinander.
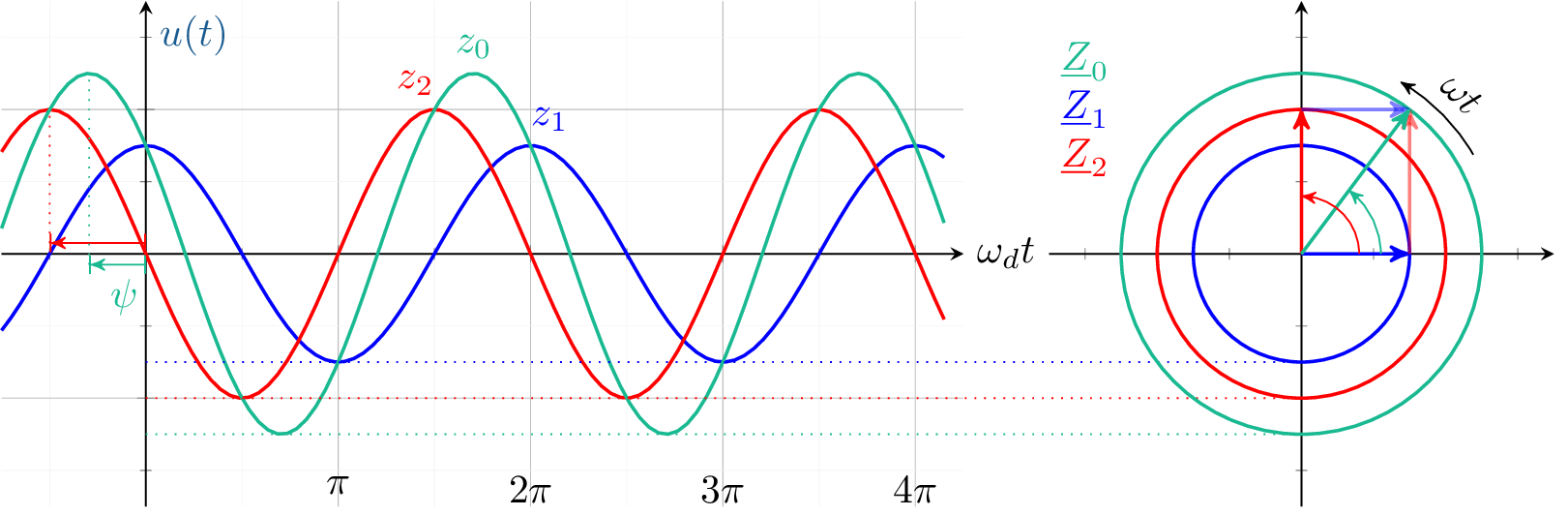
In Abbildung 8 ist die Überlagerung in Form addierter Zeitverläufe (a) und in Form addierter komplexer Amplitudenzeiger im Zeigerdiagramm (b) dargestellt. Mathematisch ausgedrückt:\begin {align} &&&{\textit {Zeitbereich}}&&&&{\textit {Polar.}}&&{\textit {Kart.}} &&\nonumber \\ && z_1(t) &= +C_1 \cdot \cos (\omega _d t)& &\Leftrightarrow & \underline {z}_1 &= C_1 \cdot \mathrm {e}^{\mathrm {j}0} & \underline {z}_1 &= C_1 \nonumber \\ && z_2(t) &= -C_2 \cdot \sin (\omega _d t)& &\Leftrightarrow & \underline {z}_2 &= C_2 \cdot \mathrm {e}^{-\mathrm {j}\frac {\pi }{2}} & \underline {z}_2 &= \hphantom {C_1} - \mathrm {j} \cdot C_2 \nonumber \\ && z_0(t) &= z_1(t) + z_2(t)& &\Leftrightarrow & \underline {z}_0 &= \underline {z}_1 + \underline {z}_2 & \underline {z}_0 &= C_1 - \mathrm {j} \cdot C_2 \nonumber \\ && &= C_0 \cdot \cos (\omega _d t + \psi )& &\Leftrightarrow & \hphantom {z_0} &= C_0 \cdot \mathrm {e}^{\mathrm {j}\psi } \nonumber \\[4pt] &\text {mit}& C_0 &= \sqrt {C_1^2 + C_2^2}& &\text {und}& \psi &= \arctan \left (-\frac {C_2}{C_1}\right ), &\varphi _0 &= \psi + \frac {\pi }{2} \nonumber \\[4pt] && z_0(t) &= C_0 \cdot \sin (\omega _d t + \varphi _0) \label {eq:dgl:rlc:homolsg:periodisch:zeigeraddition} \end {align}
Die homogene Lösung im periodischen Fall aus Gl. ?? lässt sich nach Gl. ?? wie im Folgenden als abklingende, phasenverschobene Sinuskurve beschreiben (Vgl. Gl. ??): \begin {align*} u_{C,\mathrm {h}} &= \mathrm {e}^{-\mathrm{d}elta t} \cdot C_0 \cdot \sin (\omega _d t + \varphi _0) &&\text {mit} \lambda _{1/2} = -\mathrm{d}elta \pm \mathrm {j} \cdot \omega _d \end {align*}
Die Nullstellen (NST) des charakteristiscen Polynoms, das heißt die Eigenwerte \(\lambda _{1/2}\), des RLC-Serienschwingkreises hängen von der Diskriminante \(D\) ab.
Abbildung 8a zeigt die Lage der Nullstellen im komplexen Zahlenraum als Ortskurve in Abhängigkeit von \(D\) für \(\mathrm{d}elta = \frac {R}{2L} = konst.\). Der Verlauf der NST entspricht einem Anstieg der ungedämpften Eigenkreisfrequenz \(\omega _0 = \frac {1}{\sqrt {LC}}\). [Vgl. Gl. ??]
Im aperiodischen Fall (\(D>0\)) bewegen sich die beiden negativen reellen NST für \(\mathrm{d}elta =konst.\) und steigendem \(\omega _0\) auf einander zu. Die NST näher an der Imaginärachse dominiert das Einschwingverhalten des Systems (langsamerer Abklingvorgang). Im aperiodischen Grenzfall (\(D=0\)) verschmelzen die NST zu einer doppelten Nullstelle bei \(\lambda _{1/2}=-\mathrm{d}elta \). Im periodischen Grenzfall (\(D<0\)) bewegen sich die konjugiert komplexen NST für \(\mathrm{d}elta =konst.\) und steigendem \(\omega _0\) parallel zur Imaginärachse und entfernen sich von der Realachse.
Vergleich: Polstellen der Übertragungsfunktion (Systemtheorie)
Aus der Lage der Eigenwerte im Ortskurvendiagramm lassen sich Rückschlüsse auf das Einschwingverhalten des RLC-Serienschwingkreises ziehen. Das Vorgehen ist üblich bei der Stabilitätsanalyse von Systemen im Rahmen der Regelungstechnik und stammt als Methode aus der Systemtheorie.
Für verschwindende Anfangsbedingungen (\(\frac {\mathrm {d}^{i}}{\mathrm {d}t^{i}}\,u_C(0)=0\ \forall i\)) lässt sich die DGL aus Gl. ?? mithilfe der Laplace-Transformation direkt im Bildbereich beschreiben. Durch umstellen der transformierten Ausgangsgröße \(U_C(s)\) nach der Eingangsgröße \(U(s)\) ergibt sich die Übertragungsfunktion \(G(s)\) des RLC-Serienschwingkreises:
\begin {align} u(t) &= LC \cdot \frac {\mathrm {d}^{2}}{\mathrm {d}t^{2}}\,u_{C}(t) + RC \cdot \frac {\mathrm {d}}{\mathrm {d}t}\,u_{C}(t) + u_{C}(t)& &\bigg |\,\mathscr {L}\\ U(s) &= LC \cdot s^2 \cdot U_C(s) + RC \cdot s \cdot U_C(s) + U_C(s) \vphantom {\bigg |}\\ G(s) &= \frac {U_C(s)}{U(s)} = \frac {\text {Ausgangsgröße}(s)}{\text {Eingangsgröße}(s)} \vphantom {\bigg |}\\ &= \frac {1}{LC \cdot s^2 + RC \cdot s + 1} \end {align}
Die Polstellen der Übertragungsfunktion \(G(s)\) entsprechen den Eigenwerten \(\lambda _{1/2}\).
Im periodischen Fall ergibt sich die (gedämpfte) Eigenkreisfrequenz \(\omega _d\) und die Abklingkonstante \(\mathrm{d}elta \) aus den Eigenwerten \(\lambda _{1/2}\). Die Größen hängen eng zusammen mit der Güte \(Q_{\mathrm {S}}\) und der Resonanzkreisfrequenz \(\omega _0\) eines Schwingkreises (Resonanzkreises). Beide Größen werden als Kenngrößen für Schwingkreise verwendet und ausführlicher in Modul 8 (Frequenzvariable Schaltungen) behandelt.
Der Zusammenhang zwischen \(\omega _d\), \(\mathrm{d}elta \), \(\omega _0\) und \(Q_{\mathrm {S}}\) soll anhand des RLC-Serienschwingkreises aus Abbildung 5a erläutert werden. Die Eigenwerte \(\lambda _{1/2}\) sind nach Gleichung ?? gegeben durch: \begin {align} \lambda _{1/2} &= -\underbrace { \vphantom {\sqrt {\left (\frac {R}{2L}\right )^2}} \frac {R}{2L} }_{\mathrm{d}elta } \pm \, \mathrm {j} \cdot \underbrace { \sqrt {\frac {1}{LC} - \left (\frac {R}{2L}\right )^2} }_{\omega _d} \label {eq:dgl:rlc:lambda:periodisch:exkurs} \end {align}
Der negative Realteil \(-\mathrm{d}elta \) bestimmt die Abklingrate und der Imaginärteil \(\omega _d\) die Kreisfrequenz der linear gedämpften, harmonischen Schwingung. Die Eigenkreisfrequenz \(\omega _d\) lässt sich mit Gl. ?? auch in Abhängigkeit von \(\omega _0\) und \(\mathrm{d}elta \) ausdrücken.\begin {align} \omega _d &= \sqrt {\frac {1}{LC} - \left (\frac {R}{2L}\right )^2} = \sqrt {\omega _0^2 - \mathrm{d}elta ^2} \label {eq:dgl:rlc:eigenkreisfrequenz} \end {align}
Das hat den Vorteil, dass die ungedämpfte Eigenkreisfrequenz \(\omega _0\) und die Abklingkonstante \(\mathrm{d}elta \) direkt aus den Koeffizienten der DGL abgelesen werden können. Hierfür bietet sich die Form: \begin {equation} \mathrm{d}dot y + 2\mathrm{d}elta \cdot \mathrm{d}ot y + \omega _0^2 \cdot y = b \end {equation}
für gewöhnliche, homogene, lineare DGLen 2. Ordnung an. Die DGL beschreibt das Verhalten linearer gedämpfter Systeme zweiter Ordnung (mit zwei Energiespeichern).
Die ungedämpfte Eigenkreisfrequenz entspricht dabei der Resonanzkreisfrequenz \(\omega _0\). Bei Anregung eines Schwingkreises mit dessen Resonanzfrequenz \(f_0\) tritt eine Resonanz auf. Im Resonanzfall verschwindet der Blindanteil der Gesamtimpedanz \(\underline {Z}(\omega )\) (Resonanzbedingung). [Vgl. Modul 8]
Mit der Gesamtimpedanz: \begin {align} \underline {Z}(\omega ) &= R + \mathrm {j} \left ( \omega L - \frac {1}{\omega C} \right ) \nonumber \\ \end {align}
und der Resonanzbedingung: \begin {align} \Im \{\underline {Z}(\omega _0)\} &= \omega _0 L - \frac {1}{\omega _0 C} \overset {!}{=} 0 \nonumber \\ \end {align}
folgt für die Resonanzkreisfrequenz: \begin {align} \omega _0 &= \sqrt {\frac {1}{LC}} \label {eq:dgl:rlc:resonanzkreisfrequenz} \end {align}
Die Güte \(Q_{\mathrm {S}}\) als Maß für die Schwingungsfähigkeit eines Schwingkreises lässt sich ebenfalls aus \(\omega _0\) und \(\mathrm{d}elta \) ableiten. Sie ist definiert als Verhältnis der schaltungsintern schwingenden Blindleistung zur schaltungsinternen Verlustleistung im Resonanzfall. Dies entspricht beim RLC-Serienschwingkreis dem Verhältnis von Blindwiderstand der Induktivität \(X_{L,0}\) bei Resonanzfrequenz zur Serienresistenz \(R\) (ohne Herleitung). Dadurch ergibt sich folgender Zusammenhang:
\begin {align} Q_{\mathrm {S}} &= \frac {X_{L,0}}{R} = \frac {\omega _0 L}{R} = \frac {\omega _0}{2\mathrm{d}elta } \label {eq:dgl:rlc:guete} \end {align}
Die Güte ist proportional zum Verhältnis der ungedämpften Eigenkreisfrequenz zur Dämpfungskonstante.
...