Leitfähigkeit und Widerstand
Die Leitfähigkeit oder auch der Leitwert \(G\) beschreibt, wie der Name schon impliziert, die Fähigkeit eines Materials elektrischen Strom zu leiten. Je größer der Wert, desto besser leitet ein Material, sprich, umso einfacher können sich die Ladungsträger im Material bewegen. Diese Eigenschaft basiert auf den Experimenten eines deutschen Experimentalphysikers Georg Simon Ohm anfang des 19. Jahrhunderts, in welchen er herausfand, dass sich der Strom proportional zur angelegten Spannung verhält. Der Kehrwert des Leitwertes ist der heute gebräuchlichere ohm’sche Widerstand \(R\). Der Leitwert \(G\) hat die Einheit Siemens (S), der ohmsche Widerstand die Einheit Ohm (\(\Omega \)).
In der Schaltungsentwicklung wird die physikalische Eigenschaft des ohm’schen Widerstandes genutzt, um die gewünschten Funktionen zu realisieren. Die Abbildung 1 zeigt verschiedene Ausführungen des Bauelements elektrischer Widerstand. Unabhängig von der Ausführung, basieren alle ohm’schen Widerstände auf den grundlegenden Prinzipien der Physik, auf welche im Folgenden näher eingegangen wird.
Lernziele: Leitfähigkeit und Widerstand
Die Studierenden
- kennen das elektrische Bauelement Widerstand.
- können die unterschiedlichen Bauteilausführungen von Widerständen erklären.
- können anhand des spezifischen Widerstand \(\rho \) oder des spezifischen Leitwertes \(\kappa \) Berechnungen durchführen.
- können die Unterschiede in der Leitfähigkeit verschiedener Materialien basierend auf deren atomarer Struktur und Temperatur analysieren.
1 Die elektrische Leitfähigkeit
Aus Modul 1 ist die Definition der Stromdichte \(J\) und des Stromes \(I\) bekannt. Durch Einsetzen der Formeln 2 und 3 in Formel 1 ergibt sich die Formel 4:
\begin {equation} \label {eq:dI/dA} J=\frac {\Delta I}{\Delta A} \end {equation}
\begin {equation} \label {eq:dQ/dt} I = \frac {\Delta Q}{\Delta t} \end {equation}
\begin {equation} \label {eq:dV/dx} \Delta V=\Delta A \cdot \Delta x \Leftrightarrow \Delta A = \frac {\Delta V}{\Delta x} \end {equation}
\begin {equation} \label {eq:J=.} J=\frac {\Delta Q \cdot \Delta x }{\Delta t \cdot \Delta V} \end {equation}
Durch Einsetzen der aus Modul 1 bekannten Driftgeschwindigkeit \(v_{\mathrm {el}}\) und der Raumladungsdichte \(\rho \) in die Formel 4, ergibt sich die Formel 7 für die Stromdichte.
\begin {equation} v_{\mathrm {el}}=\frac {\Delta x}{\Delta t} \end {equation}
\begin {equation} \rho = \frac {\Delta Q}{\Delta V} \end {equation}
\begin {equation} \label {eq:J=rho*v} \vec {J}=\rho \cdot \vec {v_{\mathrm {el}}} \end {equation}
Da die Geschwindigkeit immer einen Betrag und eine Richtung hat, ist die Stromdichte ebenfalls ein Vektor.
Die Driftgeschwindigkeit \(\vec {v_{\mathrm {el}}}\) der freien Ladungsträger verhält sich proportional zum elektrischen Feld \(\vec {E}\), jedoch in entgegengesetzter Richtung. Der Proportionalitätsfaktor wird auch als Elektronenbeweglichkeit \(\mu _e\) bezeichnet.
\begin {equation} \vec {v_{\mathrm {el}}}=- \mu _e \cdot \vec {E} \end {equation}
Die Raumladungsdichte \(\rho \) setzt sich aus der Elementarladung \(e^-\) und der Ladungsträgerdichte \(n_e\), zusammen. Aufgrund der negativen Ladung von Elektronen, ergibt sich ein negatives Vorzeichen.
\begin {equation} \rho = - n_e \cdot e^- \end {equation}
Das Einsetzen von \(\vec {v_{\mathrm {el}}}\) und \(\rho \) in die Formel 7 ergibt den folgenden Ausdruck:
\begin {equation} \vec {J} = (-n_e \cdot e^-) \cdot (-\mu _e \cdot \vec {E}) = n_e \cdot \mu _e \cdot e^- \vec {E} \end {equation}
Die materialabhängigen Komponenten \(n_e\) und \(\mu _e\) sowie die Naturkonstante \(e^-\) ergeben multipliziert die spezifische Leitfähigkeit \(\kappa \):
\begin {equation} \kappa = n_e \cdot \mu _e \cdot e^- \end {equation}
Zusammengefasst ergibt diese Darstellung die Beschreibung des ohmschen Gesetzes:
\begin {equation} \label {eq:E=J/k} \vec {J}=\kappa \cdot \vec {E} \, \Leftrightarrow \, \vec {E}=\frac {\vec {J}}{\kappa } \end {equation}
\begin {equation} \label {eq:u=Eds} U_{12}=\int _{P_1}^{P_2} \vec {E} \cdot \mathrm {d}\vec {s} \end {equation} Da das elektrische Feld parallel zur Leitungslänge verläuft, ergibt sich das Skalarprodukt:
\begin {equation} U_{12}=\int _{s=0}^{s=l} \vec {E} \cdot \mathrm {d}\vec {s} \end {equation} Durch Einsetzen der umgestellten Formel 12 nach \(\vec {E}\), folgt:
\begin {equation} U_{12}=\int _{0}^{l} \frac {J}{\kappa } \cdot \mathrm {d}s \end {equation}
Da es sich um ein homogenes Material handelt ist das \(\kappa \) konstant.
\begin {equation} U_{12}=\frac {1}{\kappa } \cdot \int _{0}^{l} J \cdot \mathrm {d}s \end {equation} Die folgende Formel für die Stromdichte \(J\) ist aus Modul 1 bekannt:
\begin {equation} J=\frac {I}{A} \end {equation} Duch Einsetzen der Formel ergibt sich folgender Ausdruck:
\begin {equation} U_{12}=\frac {1}{\kappa }\cdot \int _{0}^{l} \frac {I}{A} \cdot \mathrm {d}s \end {equation}
Da die Querschnittsfläche \(A\) ebenfalls konstant ist, kann das Integral aufgelöst werden:
\begin {equation} U_{12}=\frac {1}{\kappa }\cdot \frac {I}{A} \cdot l \end {equation}
Durch Umstellung ergibt sich:
\begin {equation} U_{12}=\frac {l}{A\cdot \kappa }\cdot I \end {equation}
Da \(\frac {l}{A\cdot \kappa }\) der elektrische Widerstand ist, ergibt sich folgende Vereinfachung:
\begin {equation} U=R \cdot I \end {equation}
Die elektrische Leitfähigkeit sagt aus, wie gut ein Material Ladungsträger transportieren kann, also wie gut elektrischer Strom durch sie fließt. Sehr gut leitfähige Materialien werden Leiter (im Extremfall auch Supraleiter) genannt, während sehr schlecht leitende Materialien als Isolatoren bezeichnet werden. Zu den leitfähigen Medien zählen Metalle wie Kupfer, Silber, Aluminium und Gold, welche in der Elektrotechnik am häufigsten verwendet werden. Als Isolatoren werden zum Beispiel Kunststoffe (Polyethylen (PE), Polytetrafluorethylen (PTFE oder Teflon), Polyvinylchlorid (PVC) etc.), speziell für die Anwendung als Isolator hergestellte Mineralöle, Silikone und Epoxidharz (z.B. als Vergussmasse) oder auch Papier verwendet. Des Weiteren gibt es Halbleiter wie Silizium und Germanium, deren Leitfähigkeit zwischen denen von Leitern und Isolatoren einzuordnen sind. Ihre Leitfähigkeit kann durch Dotierung und äußere Einflüsse wie Temperatur und Licht verändert werden. Diese Eigenschaften werden bei Bauteilen wie Dioden oder Transistoren genutzt, um bestimmte Funktionen zu realisieren. Die verschiedenen Arten und Eigenschaften von Halbleiter sind sehr umfangreich und werden in späteren Modulen behandelt. Vollständigkeitshalber sei noch erwähnt, dass flüssige Medien wie Säuren oder Salzlösungen leitfähig sind und als Elektrolyt bezeichnet werden. Außerdem gibt es auch ionisierte Gase, die frei bewegliche Ladungsträger enthalten und elektrische Ströme leiten können. Diese leitfähigen Gase werden Plasmen genannt, welche in diesem Modul ebenfalls nicht behandelt werden.
2 Driftverhalten von Elektronen in Leitern
In Modul 1 wurde bereits vermittelt, dass der elektrische Stromfluss die gerichtete Bewegung von freien Ladungsträgern ist. Im Fall eines Leiters sind dies die negativen Ladungsträger, also die Elektronen, welche sich frei im Material bewegen können. Die Struktur eines solchen Materials besteht aus einem festen Gitter von Atomrümpfen und frei beweglichen Elektronen. Sowohl die Beweglichkeit der Elektronen \(\mu _{\mathrm {e}}\), als deren Anzahl, ist materialabhängig. Im feldfreien Raum bewegen sich diese Elektronen zufällig in alle Richtungen, was zu einem neutralen Zustand führt. Da es sich hierbei um keine gerichtete sondern um eine in alle Richtungen gleichverteilte Bewegung handelt, ist kein Stromfluss feststellbar. Dennoch führt diese ungerichtet, von der Temperatur abhängige, Bewegung der Ladungsträger zu elektrotechnischen Effekten: In empfindlichen Schaltungen wird sie als Rauschen wahrgenommen. Die freien Ladungsträger sind sehr viel leichter als die im Gitter verankerten Atomrümpfe, so dass es bei einem Aufprall eines in Bewegung befindlichen Elektrons auf einen Atomrumpf zu einem unelastischen Stoss kommt und sich die Bewegungsrichtung des Elektrons ändert. Dieses Verhalten ist in Abbildung 2 zu sehen.
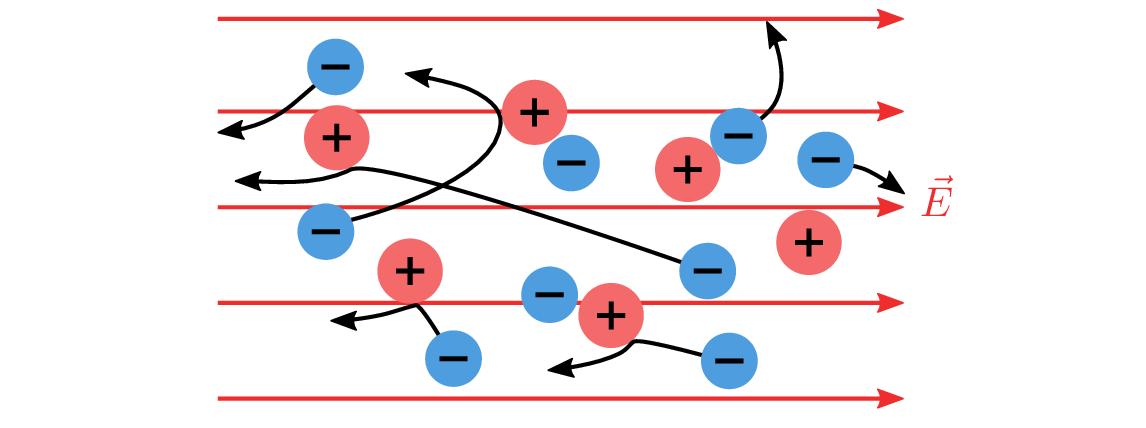
Sobald sich ein Leiter in einem elektrischen Feld befindet, wirkt auf die Elektronen die Coulomb-Kraft, so dass sich ihre zufällige Bewegungsrichtung in eine gerichtete Bewegung ändert, welche entgegengesetzt zur Feldrichtung zeigt (Abb. 3). Diese gerichtete Bewegung der Ladungsträger wird als Stromfluss bezeichnet (vgl. Modul 1). Allerdings kommt es auch weiterhin zu Stößen mit den Atomrümpfen. Diese führen letztlich zu einer Abschwächung der gerichteten Bewegung und somit des Stroms (vgl. Abb. 3). Da sich die Atomrümpfe mit steigender Temperatur stärker bewegen, nimmt die Stoßwahrscheinlichkeit der Elektronen bei steigender Temperatur zu.
Dieses Verhalten der Elektronen wird auch Driftverhalten genannt, welches stark vom Material anhängt. Da die atomare Zusammensetzung materialabhängig ist, unterscheidet sich auch die Anzahl der freien Elektronen, sowie deren Beweglichkeit \(\mu _{\mathrm {e}}\). Diese beiden Eigenschaften werden unter dem Begriff der spezifischen Leitfähigkeit \(\kappa \) zusammengefasst. Mit der spezifischen Leitfähigkeit kann somit die Driftgeschwindigkeit der Elektronen in der Gitterstruktur des Leiters ermittelt werden. Der folgende Abschnitt befasst sich mit eben diesen Eigenschaften.
3 Mathematische Zusammenhänge der Leitfähigkeit
Die unterschiedlichen atomaren Zusammensetzungen der Materialien führen zu einer materialabhängigen, elektrischen Leitfähigkeit. Die materialspezifische Eigenschaft bestehen aus der spezifischen Leitfähigkeit \(\kappa \) (Kappa), bzw. dem spezifischen Widerstand \(\rho _\mathrm {R}\) (rho) welche antiproportional zueinander stehen, sowie dem jeweiligen Temperaturkoeffizient \(\alpha \), welcher sich je nach Material unterscheidet.
\begin {equation*} [\kappa ] = 1\,\, \frac {\text {Siemens}}{\text {m}} = 1\,\, \frac {\text {S}}{\text {m}} = 1\,\, \frac {\text {1}}{\Omega \cdot \text {m}} \end {equation*} \begin {equation} \kappa = \frac {1}{\rho _\mathrm {R}} \end {equation}
\begin {equation} \rho _\mathrm {R} = \rho _\mathrm {{20^\circ C}} \cdot (1 + \alpha (\vartheta - 20\mathrm {^\circ C})) \end {equation} Für \(\vartheta \) (Theta) wird die Temperatur des Leiters eingetragen. Daraus ergibt sich durch (\(\vartheta - 20\mathrm {^\circ C}\)) die Temperaturdifferenz des Leiters zwischen der vorhandenen Temperatur des Leiters und den \(\mathrm {20^\circ C}\), bei welchen der Referenzwert ermittelt wurde. Werden \(20\mathrm {^\circ C}\) für \(\vartheta \) (Theta) eingesetzt, fällt auch das \(\alpha \) weg und es bleibt der Referenzwert \(\rho _\mathrm {20\mathrm {^\circ C}}\) übrig. In der folgenden Tabelle sind beispielhaft einige Materialien mit deren spezifischen Eigenschaften dargestellt:
| Material | Spezifische Leitfähigkeit [\(\kappa \)] = S/m | Temperaturkoeffizient [\(\alpha \)] = 1/K |
| Silber | \(6.1\cdot 10^{7}\) | 0.0038 |
| Kupfer | \(5.8 \cdot 10^{7}\) | 0.0038 |
| Gold | \(4.5 \cdot 10^{7}\) | 0.0034 |
| Aluminium | \(3.7 \cdot 10^{7}\) | 0.004 |
| Eisen | \(1.0 \cdot 10^{7}\) | 0.0065 |
| Graphit | \(3 \cdot 10^{6}\) | -0.0002 |
| Silizium (dotiert) | \(1 - 10^6\) | -0.075 |
| Leitungswasser | \(5.0 \cdot 10^{-3}\) | - |
| Luft | \(4.0 \cdot 10^{-15}\) | - |
Äquivalent zur spezifischen Leitfähigkeit \(\kappa \) und zum spezifischen Widerstand \(\rho _\mathrm {R}\), kann der entsprechende Widerstand \(R\), bzw. Leitwert \(G\) eines Körpers bestimmt werden.
\begin {equation*} [G] = 1\, \text {Siemens} = 1\, \text {S} = 1\,\, \frac {\text {1}}{\Omega } \end {equation*} \begin {equation} G = \frac {1}{R} \end {equation}
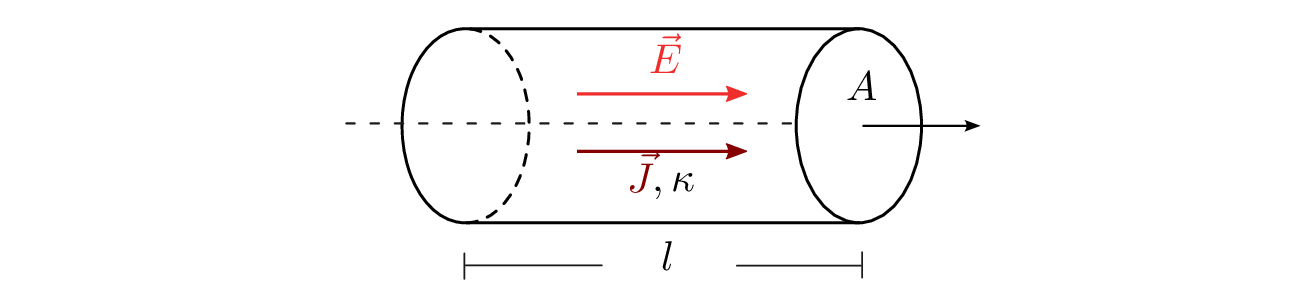
Der Wert der elektrischen Leitfähigkeit bzw. des Widerstandes eines Leiters, ergibt sich darüber hinaus aus den geometrischen Eigenschaften. Sowohl die Länge \(l\) als auch die Querschnittsfläche \(A\) tragen zum Leitwert bzw. Widerstandswert bei. Abbildung 4 zeigt einen solchen Leiter mit seinen Eigenschaften.
Die Stromdichte \(\vec {J}\) ergibt sich dabei aus dem elektrischen Feld \(\vec {E}\) und der spezifischen Leitfähigkeit \(\kappa \). Die Stromdichte ist dabei geometrieunabhängig. Erst zur Berechnung des Stromes \(I\) müssen die Länge und die Querschnittsfläche mit einbezogen werden. Mit der folgenden Formel lässt sich der Widerstandswert berechnen:
\begin {equation*} [R] = 1\, \text {Ohm} = 1\, \text {$\Omega $} \end {equation*} \begin {equation} R = \rho _\mathrm {R} \cdot \frac {l}{A} \end {equation}
\begin {align*} \rho _\mathrm {R} & : \text {spezifischer Widerstand des Materials } (\Omega \text {m}) \\ l & : \text {Länge des Materials (m)} \\ A & : \text {Querschnittsfläche des Materials } (\text {m}^2) \\ \end {align*}
Einführung in die Darstellung von Schaltkreisen
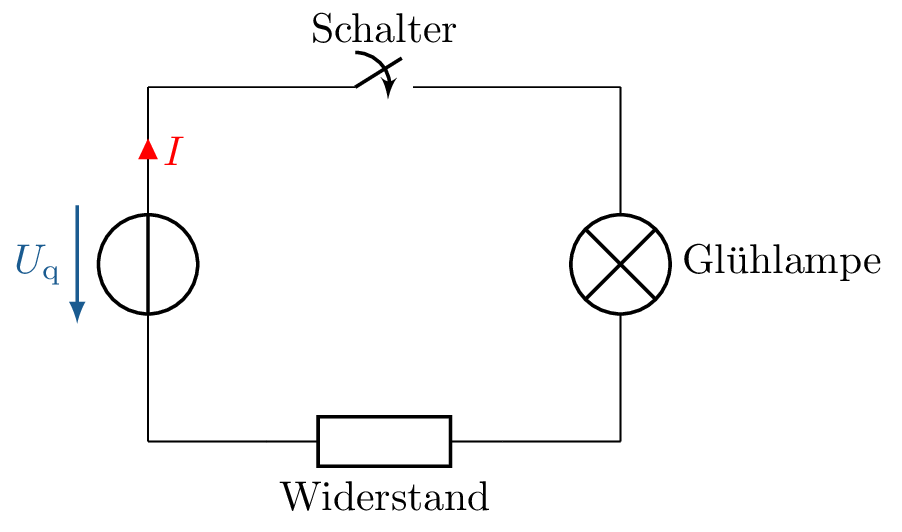
In der Elektrotechnik werden zur Darstellung von elektrischen Netzwerken sogenannte Schaltbilder verwendet. Inhalt dieser Schaltbilder sind Schaltsymbole, welche für die elektrischen Eigenschaften bzw. ganze Bauelemente, verwendet werden. Abbildung 5 zeigt beispielhaft ein solches Schaltbild.
Das Schaltbild besteht aus vier Elementen, welche mit Linien verbunden sind. Es stellt eine Reihenschaltung bestehend aus einer Spannungsquelle, einem Schalter, einer Glühlampe und einem Widerstand, dar. Der Widerstand stellt den Leitungswiderstand der gesamten Leitung dar, während die Verbindungslinien per Definition ideale Verbindungen ohne weitere Eigenschaften darstellen.
Des Weiteren ist eine Spannung \(U_{\mathrm {q}}\), sowie der Strom \(I\) eingezeichnet, welcher jedoch erst fließen kann, wenn der Schalter geschlossen wird. Im Folgenden werden die drei grundlegenden elektrischen Eigenschaften, sowie deren Schaltsymbole tiefer behandelt.
4 Widerstand als Bauelement
Mit Hilfe der im vorherigen Abschnitt kennengelernten Methode zu Berechnung des Widerstandes, kann der Widerstandswert elektrischer Leitungen, oder auch anderer leitender Objekte, ermittelt werden. Sobald ein Widerstandswert bekannt ist, wird dieser in elektrischen Schaltbildern einem Schaltsymbol zugeordnet. So können verschiedene Komponenten und deren Eigenschaften miteinander verbunden werden, um deren Verhalten zu ermitteln. Abbildung 6 zeigt zwei gängige Schaltzeichen für den Widerstand.
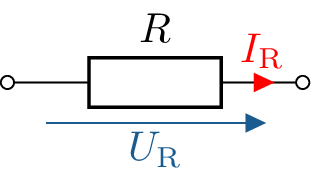
Sobald eine Gleichspannungsquelle an einen Widerstand \(R\) angeschlossen wird, verhalten sich Strome und Spannungen linear. Abbildung 7 zeigt den durch den Widerstand fließenden Strom \(I_\mathrm {R}\), sowie die abfallende Spannung \(U_\mathrm {R}\).
Das Schaltsymbol des Widerstandes wird in Schaltungen immer als idealer Widerstand berücksichtigt. Unter Vernachlässigung der Temperaturabhängigkeit trifft dies im Gleichspannungsfall auch weitestgehend zu (Schaltvorgänge ausgenommen). In der Realität gibt es viele Situationen, in denen ein realer Widerstand kein lineares Verhalten aufweisen kann. Verschiedene Quellenarten werden im Abschnitte 1.2 zu Spannungs- und Stromquellen behandelt. Zum Verständnis der Abbildung 8 ist es ratsam, zuvor die Abschnitte 1.3 und 1.4 gelesen zu haben.
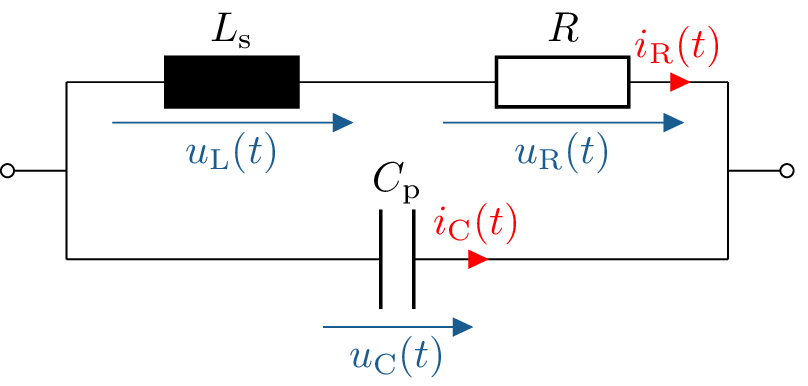
Ausgehend von der Ausführung eines Widerstandes und der Frequenz, bei welcher er betrieben wird, machen sich sogenante parasitäre Effekte bemerkbar. In Abbildung 8 ist das Ersatzschaltbild eines realen Widerstanders dargestellt. Wird dieser bei höheren Frequenzen betrieben, können die parasitären Eigenschaften (parasitics) überwiegen und zu einem völlig anderen Verhalten führen. Mehr dazu in späteren Modulen.
Im Folgenden werden aber immer vollständige Ersatzschaltbilder angenommen. Wird ein Widerstand nur mit seinem Schaltungssymbol dargestellt, soll dieser als damit vollständig beschrieben angenommen werden. Dies gilt auch für alle im Weiteren hergeleiteten Bauelemente.
In der Elektrotechnik werden werden Widerstände, auch Festwiderstände genannt, in der Schaltungsentwicklung verwendet. Eine der bekanntesten Ausführungen sind die THT-Widerstände (Through-Hole Technology). Obwohl diese Art in vielen Anwendungen von SMD-Bauteilen (Surface-Mount Device) abgelöst worden sind, gibt es immer noch Anwendungsfälle in denen sie Sinn machen. Beispiele sind Prototyping, DIY-Projekte, Leistungsanwendungen oder Leiterplatten mit hohen mechanischen Anforderungen. Die THT-Widerstände sind durch farbige Ringe gekennzeichnet, welche Aufschluss über den Widerstandswert und die Toleranz liefern. Abbildung 9 zeigt einen THT-Widerstand mit dem dazugehörigen Ableseschema und einer Tabelle zum Ablesen der Werte:
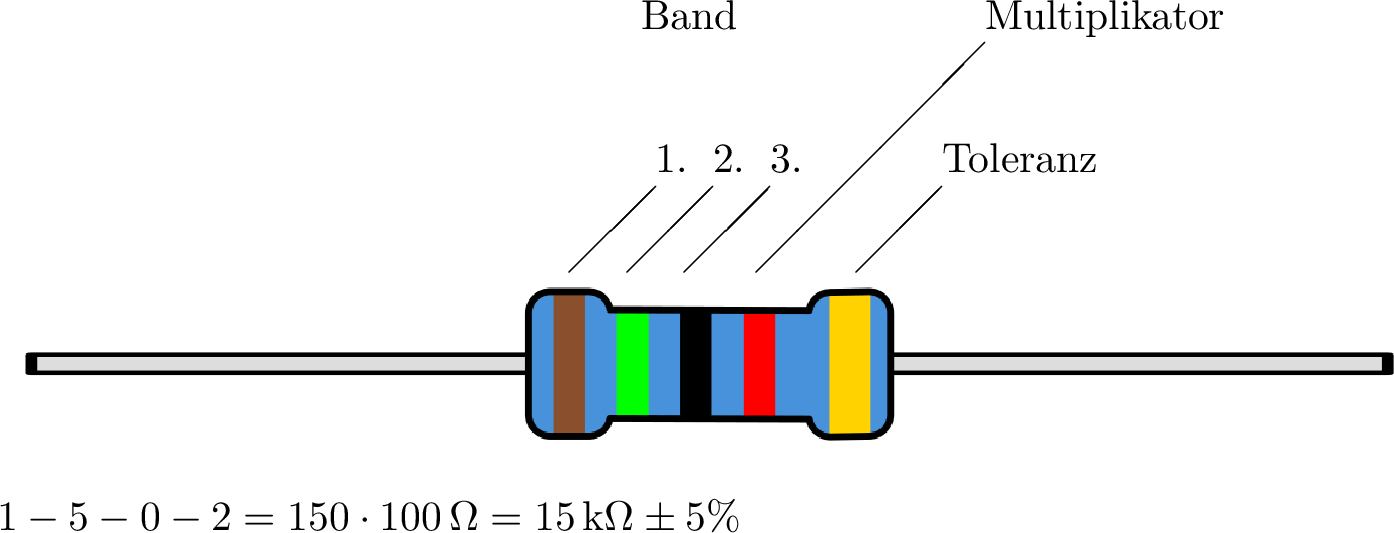
| Farbe | 1. 2. 3. Band | Multiplikator | Toleranz | ||
| Schwarz | 0 | \(1\,\Omega \) | - | ||
| Braun | 1 | \(10\,\Omega \) | \(\pm \, 1\,\%\) | ||
| Rot | 2 | \(100\,\Omega \) | \(\pm \, 2\,\%\) | ||
| Orange | 3 | \(1\,\text {k}\Omega \) | - | ||
| Gelb | 4 | \(10\,\text {k}\Omega \) | - | ||
| Grün | 5 | \(100\,\text {k}\Omega \) | \(\pm \, 0.5\,\%\) | ||
| Blau | 6 | \(1\,\text {M}\Omega \) | \(\pm \, 0.25\,\%\) | ||
| Violett | 7 | \(10\,\text {M}\Omega \) | \(\pm \, 0.1\,\%\) | ||
| Grau | 8 | - | \(\pm \, 0.05\,\%\) | ||
| Weiß | 9 | - | - | ||
| Gold | - | \(0.1\,\Omega \) | \(\pm \,5\,\%\) | ||
| Silber | - | \(0.01\,\Omega \) | \(\pm \,10\,\%\) | ||
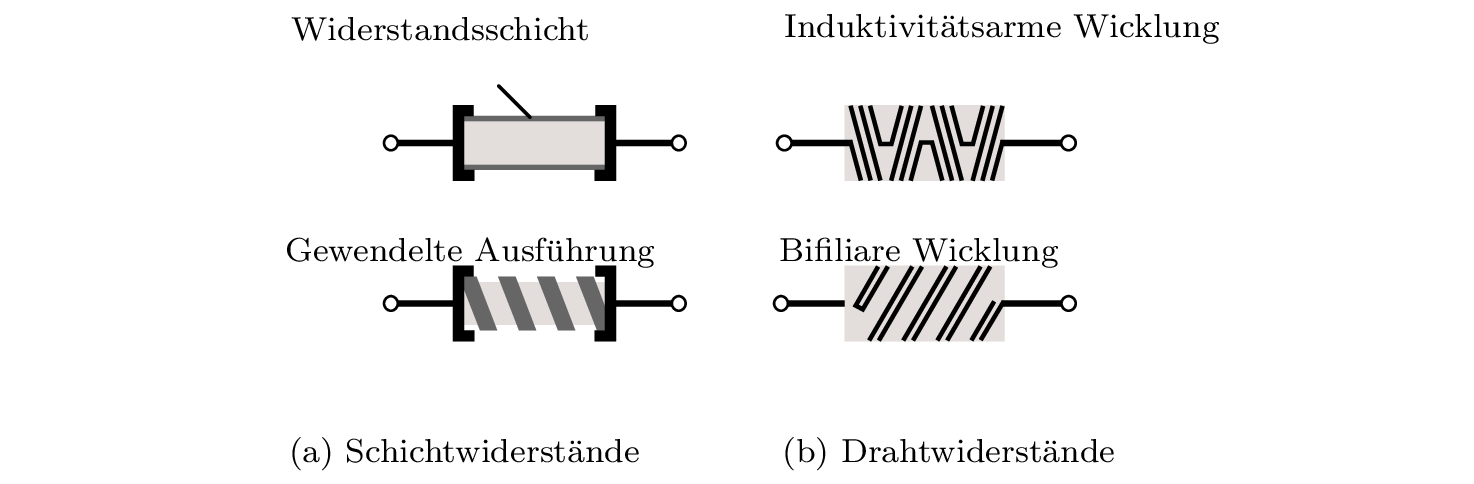
Die THT-Widerstände gibt es in verschiedenen Ausführungen, welche alle ihre Vor- und Nachteile mit sich bringen. Die Abbildung 10 zeigt vier Arten, wie diese Umgesetzt werden können.
Merke:
Der Widerstandswert eines Materials ist abhängig von dessen geometrischen und spezifischen Eigenschaften.
5 PTC und NTC
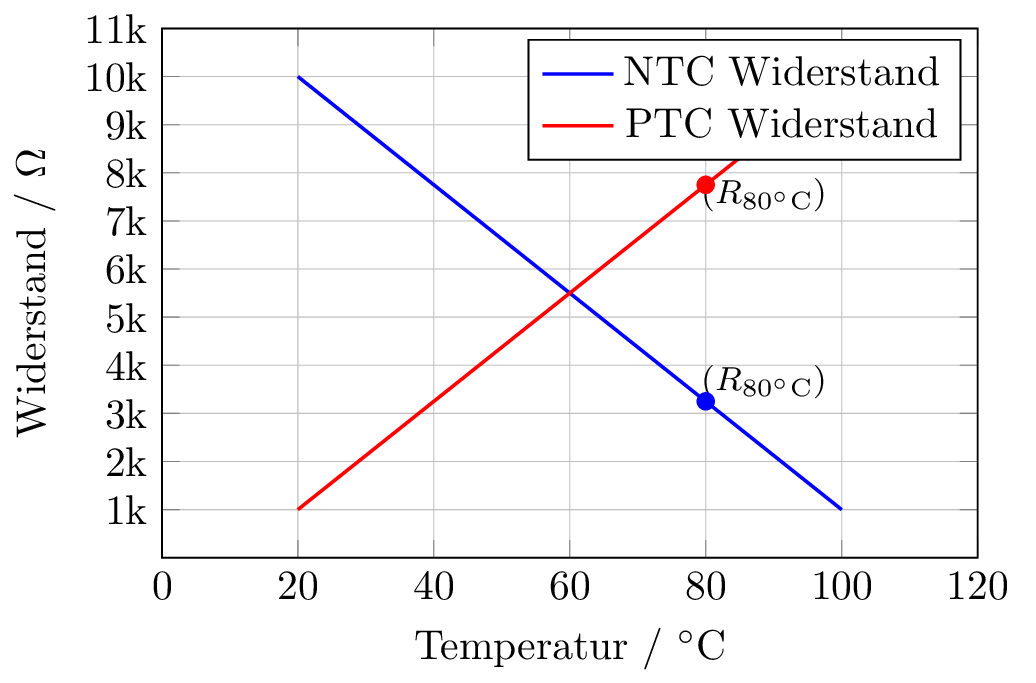
In diesem Abschnitt geht es um eine spezielle Kategorie von Widerständen, die besonders in temperaturabhängigen Anwendungen Gebrauch finden: die PTC- und NTC-Widerständen. Die Namen bezieht sich auf deren positiven bzw. negativen Temperaturkoeffizienten \(\alpha \), welcher bereits in Abschnitt 1.1.3 eingeführt wurde. Diese speziellen Widerstände, auch als Thermistoren bekannt, unterscheiden sich von herkömmlichen Widerständen dadurch, dass ihr Widerstandswert stark von der Temperatur abhängt. Abbildung 11 zeigt das entgegengesetzte Verhalten beider Widerstandsarten.
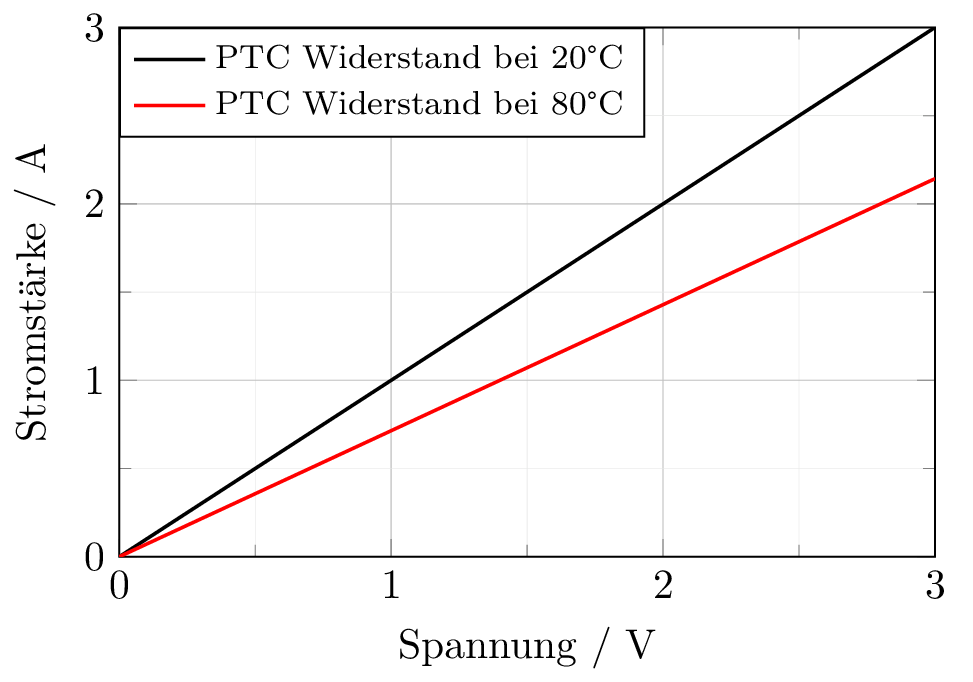
Die PTC-Widerstände haben einen positiven Temperaturkoeffizienten \(\alpha \), welcher in Tabelle 1 im Abschnitt 1.1.3 abgelesen werden kann. Gut leitfähige Materialien haben ein positives \(\alpha \), was bedeutet, dass deren Widerstand bei höheren Temperaturen zunimmt. Somit sind sie im kalten Betrieb leitfähiger, wodurch sie auch ”Kaltleiter”genannt werden. In Abbildung 12 ist der gleiche PTC-Widerstand bei jeweils unterschiedlichen Temperaturen dargestellt.
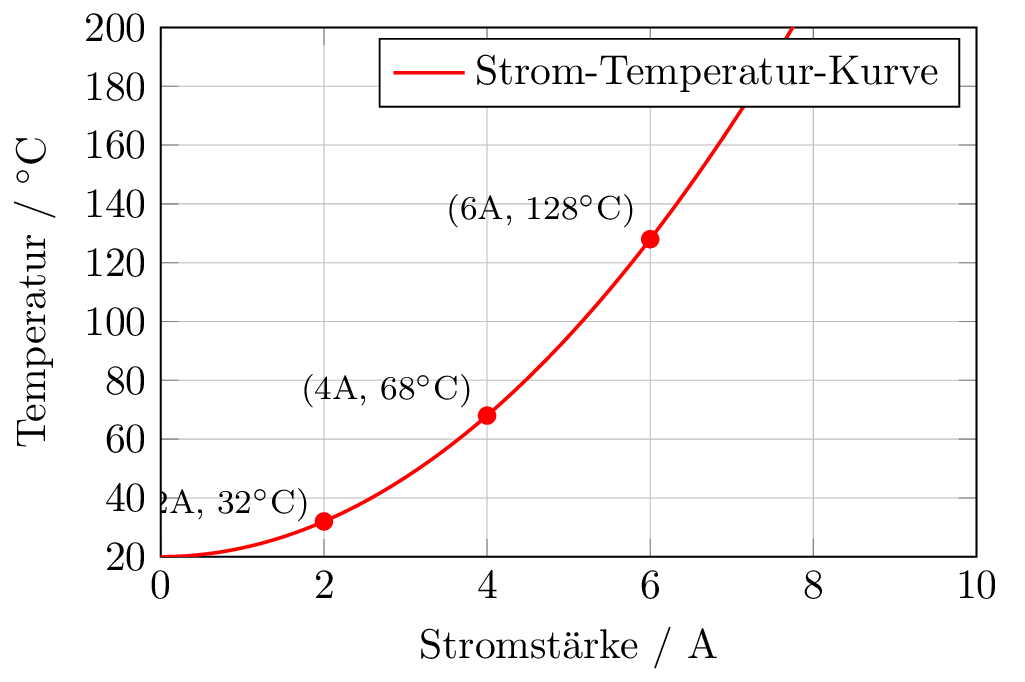
Das folgende Diagramm zeigt die Erwärmung eines PTC-Widerstandes bei Erhöhung des Stromflusses. Je mehr Strom also durch einen PTC-Widerstand fließt, desto stärker erwärmt er sich.
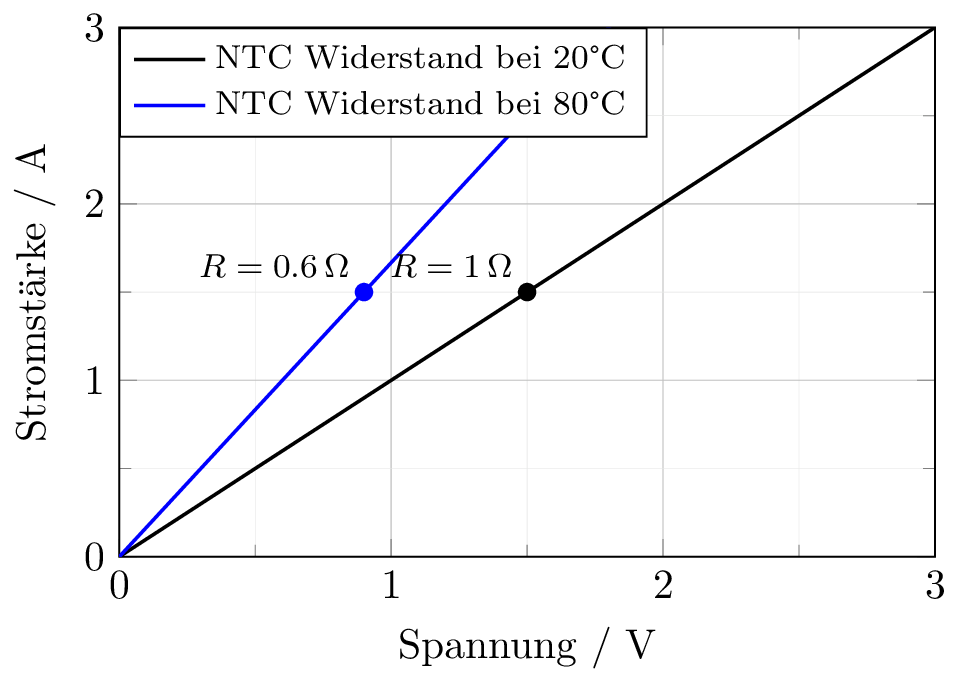
Das genau entgegengesetzte Verhalten weist ein NTC-Widerstand aufgrund seines negativen Temperaturkoeffizienten auf. Typische Materialien mit einem solchen Verhalten sind Grafit oder Silizium. Da diese Widerstände bei zunehmender Temperatur besser leiten, nennt man sie auch Heißleiter. In Abbildung 14 ist zu erkennen, dass der Widerstand bei einer höheren Temperatur einen geringeren Widerstandswert aufweist.