Spannungs- und Stromquelle
Der Betrieb elektrischer Geräte ist im Regelfall mit der Umsetzung von elektrischer Leistung verbunden. Im Modul 2 zum Thema Energie und Leistung wurde bereits vermittelt, dass Leistung der Verrichtung von Arbeit pro Zeit entspricht und dass dies einer Energieumwandlung gleichzusetzen ist. Um also elektrische Geräte, in denen ja in jedem Fall Energie umgesetzt wird, betreiben zu können, muss also Energie zugeführt werden. Energie kann nur gewandelt, nicht erzeugt werden. Dennoch wird in der Elektrotechnik das Zuführen von Energie in den zu betrachtenden Stromkreisen mit Hilfe von Strom- bzw. Spannungsquellen beschrieben. Dabei wird nicht berücksichtigt, dass es sich hierbei um eine Umwandlung von z.B. mechanischer oder chemischer in elektrische Energie handelt. Dies spielt für die Betrachtung im Stromkreis jedoch keine Rolle. Im Folgenden werden die Strom- und Spannungsquellen beschrieben und die jeweiligen Unterschiede erläutert.
Lernziele: Spannungs- und Stromquelle
Die Studierenden können
- zwischen Spannungs- und Stromquellen unterscheiden und kennen deren Schaltsymbole.
- reale Spannungs- und Stromquellen modellieren.
- Beispiele für verschiedene Quellen benennen.
1 Spannungsquellen
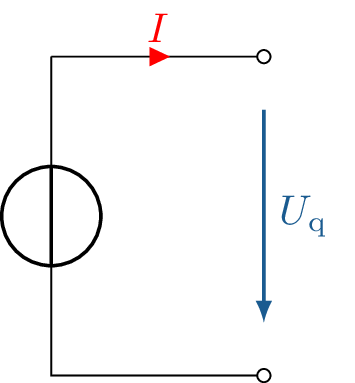
Die am häufigsten vorkommende Art der Energiequellen für elektrische Systeme ist die Spannungsquelle. Im idealen Fall zeichnet sich dadurch aus, dass sie unabhängig vom angeschlossenen Verbraucher eine konstante Spannung ausgibt. Abbildung 1 zeigt das Schaltsymbol einer idealen Spannungsquelle mit der konstanten Ausgangsspannung \(U_{\mathrm {q}}\).
In Abbildung 1 führen die Linien ins Leere, was als offene Klemmen bezeichnet wird. Da der Schaltkreis nicht geschlossen ist, fließt auch dementsprechend kein Strom. Würden in dem Fall die Klemmen kurzgeschlossen werden, dann würde die Quelle versuchen die Spannung aufrechtzuerhalten und es würde ein unendlich hoher Strom fließen. Warum dies so gefährlich ist, wird im Abschnitt 2 anhand einer realen Spannungsquelle deutlich.
2 Modellierung realer Spannungsquellen
In Schaltbildern, also der graphischen Darstellung von elektrischen Schaltkreisen, werden immer ideale Bauteile verwendet. Um das reale Verhalten von Bauelementen korrekt modellieren zu können und somit das reale Schaltungsverhalten möglichst exakt nachbilden zu können, muss das tatsächliche Verhalten des Bauelements mit Hilfe von idealen Bauteilen nachgebildet werden. Im Folgenden wird beschrieben, wie das Verhalten einer realen Spannungsquelle mit idealen Bauteilen nachgebildet werden kann. Die technische Umsetzung einer beliebigen Spannungsquelle besteht aus physischen Komponenten, welche alle bestimmte Widerstandswerte aufweisen. All diese Eigenschaften ergeben zusammengefasst den sogenannten Innenwiderstand \(R_\mathrm {i}\) einer Quelle. Im Fall der realen Spannungsquelle befindet sich der Innenwiderstand in Reihe mit der idealen Spannungsquelle. In Abbildung 2 ist eine modellierte reale Spannungsquelle zu sehen.
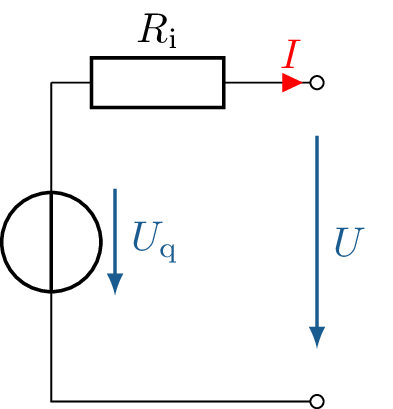
\begin {equation*} U_\mathrm {q} = U_\mathrm {R_i} + U \end {equation*}
Im Schaltbild ist zu erkennen, dass sowohl \(U_\mathrm {q}\), als auch \(U\) beide nach unten zeigen. Dies liegt am Zählpfeilsystem, welches in Modul 4 näher behandelt wird. An dieser Stelle genügt es zu wissen, dass Generatorzählpfeil und Verbraucherzählpfeil entgegengesetzt sind, da die Summe beider Pfeile Null ergeben muss. Wird nun ein Verbraucher angeschlossen, fließt der Strom über den Innenwiderstand \(R_\mathrm {i}\) durch den Verbraucher. Es wird also auch Leistung im Innenwiderstand umgesetzt.
Betrachten wir im realen Fall erneut das Verhalten bei kurzgeschlossenen Ausgangsklemmen, so wird die gesamte, von der Quelle abgegebene Leistung, lediglich am Innenwiderstand der Spannungsquelle umgesetzt. Die Leistung kann durch \(P = \frac {U^2}{R_{\mathrm {i}}}\) berechnet werden. Im Regelfall ist die Quelle dafür nicht ausgelegt, was dazu führen würde, dass sich die Energie in sehr viel Wärmeenergie umwandeln, und zur Zerstörung der Quelle führen würde.
Wird am Ausgang der Spannungsquelle eine Last mit einem Widerstand \(R_{\mathrm {L}}\) angeschlossen, so fließt ein Strom \(I\) durch die Widerstände \(R_{\mathrm {i}}\) und \(R_{\mathrm {L}}\). Dieser kann nach dem ohm’schen Gesetz und der im folgenden Modul vorgestellten Zusammenfassung von Widerständen berechnet werden zu \(I = \frac {U_{\mathrm {q}}}{(R_{\mathrm {i}} + R_{\mathrm {L}})}\). Dieser Strom führt dazu, dass am Innenwiderstand \(R_{\mathrm {i}}\) eine Spannung \(U_{\mathrm {R_{\mathrm {i}}}}\) abfällt. Im Modul 2 wurde bereits hergeleitet, dass die Summe aller Spannungen innerhalb eines geschlossenen Kreises null ergeben muss. Im Modul 4 wird hieraus die so genannte Maschenregel hergeleitet, mit deren Hilfe sich die Ausgangsspannung \(U\) berechnen lässt zu \begin {equation} U = U_{\mathrm {q}} - U_{\mathrm {R_{\mathrm {i}}}} = U_{\mathrm {q}} - I \cdot R_{\mathrm {i}} = U_{\mathrm {q}} - U_{\mathrm {q}} \cdot \frac {R_{\mathrm {i}}}{R_{\mathrm {i}} + R_{\mathrm {L}}} \end {equation}
Je kleiner also der Innenwiderstand \(R_{\mathrm {i}}\) ist, desto weniger unterscheidet sich die Ausgangsspannung \(U\) einer belasteten Spannungsquelle von der Quellspannung \(U_\mathrm {q}\). Ein im Vergleich zum Lastwiderstand \(R_{\mathrm {L}}\) möglichst kleiner Innenwiderstand \(R_{\mathrm {i}}\) sollte also für ein möglichst ideales Verhalten angestrebt werden. Dies kann u.a. mit möglichst großen Leiterqueerschnitten innerhalb der Quelle realisiert werden.
Wird die reale Spannungsquelle, modelliert mit \(U_\mathrm {q}\) und \(R_{\mathrm {i}}\), im Leerlauf betrieben, ist die Ausgangsspannung \(U\) gleich der Quellspannung \(U_\mathrm {q}\), da kein Strom durch den Innenwiderstand fließt und dort keine Spannung abfallen kann.
Beispiele für reale Spannungsquellen sind u.a. Batterien und Akkumulatoren. Dabei wird, wie weiter oben beschrieben, ein möglichst kleiner Innenwiderstand angestrebt. Eine 12-V-Starterbatterie für Autos hat einen Innenwiderstand von weniger als 10 m\(\Omega \). Auch eine Haushaltssteckdose kann als Spannungsquelle mit 230 V Quellspannung und kleinem Innenwiderstand betrachtet werden.
Merke:
- Eine Spannungsquelle darf nie kurzgeschlossen werden!
- Bei Spannungsquellen stellt sich immer der Strom ein.
3 Stromquellen
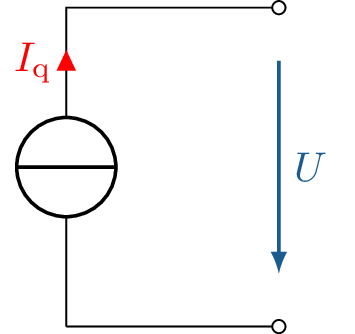
Im Vergleich zu den Spannungsquellen sind Stromquellen deutlich weniger vertreten. Sie zeichnen sich dadurch aus, dass sie einen konstanten Strom liefern und sich die Spannung entsprechend einstellt. Abbildung 3 zeigt das Schaltsymbol einer idealen Stromquelle mit dem konstanten Ausgangsstrom \(I_{\mathrm {q}}\).
Der hier dargestellte Fall einer leerlaufenden Stromquelle führt, vergleichbar mit der kurzgeschlossenen Spannungsquelle, zu einer unendlich hohen Leistungsabgabe der Quelle und muss daher vermieden werden.
4 Modelierung realer Stromquellen
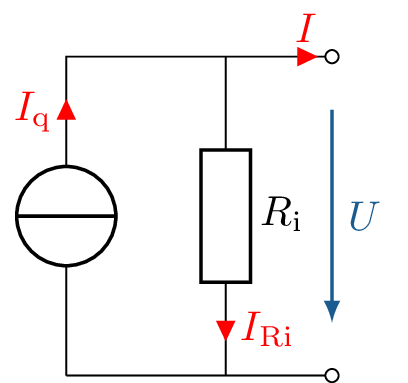
Genauso wie bei den Spannungsquelle, gibt es in der Realität auch keine idealen Stromquellen. Um das reale Verhalten einer Stromquelle beschreiben zu können, muss auch diese erst modelliert werden. Die Abbildung 4 zeigt eine solche modellierte Stromquelle.
Das Modell der realen Stromquelle setzt sich dabei ebenfalls aus dem Innenwiderstand \(R_\mathrm {i}\) und der idealen Stromquelle zusammen, wobei der Unterschied zur Spannungsquelle darin besteht, dass der Innenwiderstand parallel zur iedalen Stromquelle platziert ist. Auch hier ist der tatsächliche Ausgangsstrom kleiner als der Quellstrom \(I_{\mathrm {q}}\). Im Modul 4 wird die Knotenregel eingeführt. Diese besagt, dass die Summe aller Ströme in einem Knoten (Verzweigungspunkt) gleich null sein muss, so dass sich der Ausgangsstrom \(I\) ergibt zu
\begin {equation} I = I_{\mathrm {q}} - I_{\mathrm {R_{\mathrm {i}}}} = I_{\mathrm {q}} - \frac {U}{R_{\mathrm {i}}} \end {equation}
Je größer also der Innenwiderstand \(R_{\mathrm {i}}\) ist, desto kleiner wird der Strom \(I_{\mathrm {R_{\mathrm {i}}}}\) und desto kleiner ist die Abweichung zwischen Ausgangsstrom \(I\) un dem Quellstrom \(I_{\mathrm {q}}\).
Entgegen des dargestellten Schaltbildes darf eine Stromquelle niemals mit offenen Klemmen betrieben werden, da ähnlich wie im Fall der Spannungsquelle die gesamte Leistung im Innenwiderstand umgesetzt werden würde, was zu einer hohen thermischen Belastung und schlussendlich zur Zerstörung der Stromquelle führen würde. Beispiele für reale Stromquellen sind Solarzellen im entsprechenden Betriebszustand oder ein Labornetzteil in der Strombegrenzung.
Merke:
- Eine Stromquelle darf nie im Leerlauf betrieben werden!
- Bei Stromquellen stellt sich immer die Spannung ein.
5 Umrechnung von Spannungs und Stromquelle
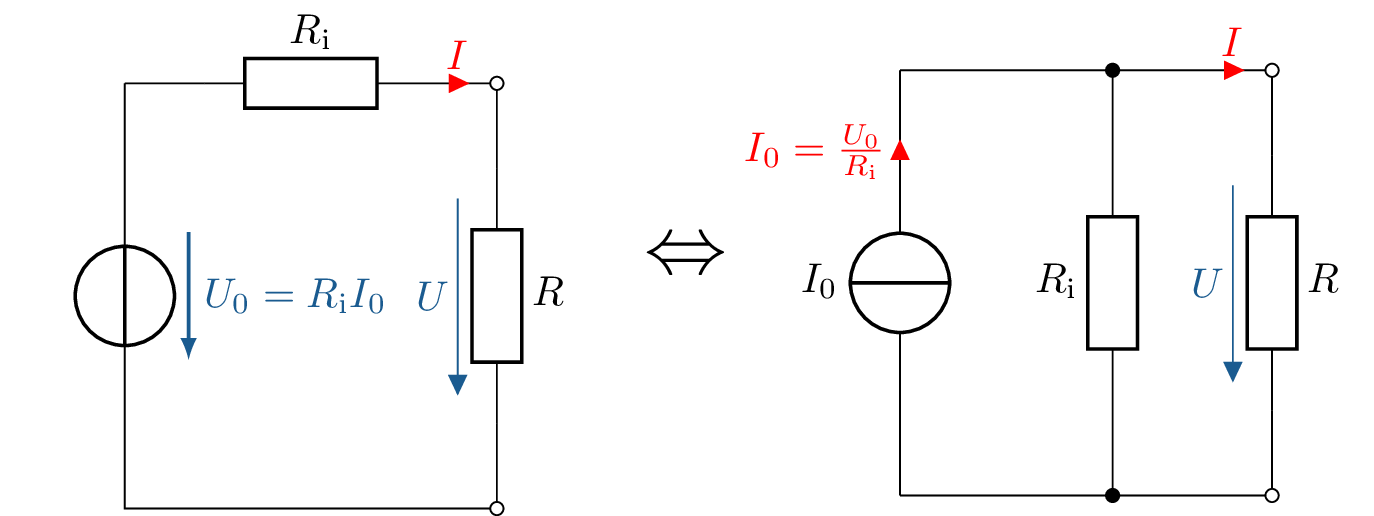
Spannungs und Stromquellen können bezüglich ihres Klemmenverhaltens ineinander umgerechnet werden. Voraussetzung dafür ist, dass sowohl der Kurzschlussstrom \(I_\mathrm {K}\) als auch die Leerlaufspannung \(U_\mathrm {L}\) bei beiden Quellen gleich sind. Abbildung 5 zeigt die Überführung der Schaltbilder ineinander. Weiterführende Inhalte zur Umrechnung und Leistungsanpassung folgen in Modul 4.
6 Verschiedene Spannungs- und Stromquellen
Die zuvor eingeführten Schaltsymbole für Spannungs- und Stromquellen sind allgemeingültig und machen keine spezifischen Aussagen über die Signalform der Ausgangsgröße. Grundsätzlich wird neben der Unterscheidung zwischen Spannungs- und Stromquellen auch zwischen Gleich- (DC, Direct Current) und Wechselspannung (AC, Alternating Current) differenziert.
Die gebräuchlichste Form für den Betrieb elektronischer Geräte ist die Gleichspannungsquelle. Sie sorgt kontinuierlich dafür, dass Ladungsträger vom Minus- zum Pluspol fließen, was ein gleichbleibendes elektrisches Feld vom Plus- zum Minuspol erzeugt.
Wechselspannungsquellen (AC) hingegen haben typischerweise eine sinusförmige Ausgangsspannung bzw. einen sinusförmigen Ausgangsstrom. Für den Energietransport über weite Strecken haben sich in der Vergangenheit Hochspannungsleitungen mit Wechselspannung durchgesetzt, da diese technisch einfacher und kostengünstiger zu realisieren waren. Der bedeutendste Vorteil von Wechselspannung ist die einfache Transformation der Spannung. Außerdem ist es praktisch, da beim Anschluss von Verbrauchern nicht auf die Verpolung geachtet werden muss.
Mittlerweile gibt es jedoch auch erste Umsetzungen des Energietransports in Form von Gleichspannung. Der
Einsatz von Gleichstrom (DC) für lange Übertragungsstrecken, wie bei den HVDC-Leitungen (High Voltage
Direct Current) von der Nordsee nach Süddeutschland, bietet einige Vorteile: Gleichstrom ist effizienter, da
er keine Blindleistung erzeugt, was bedeutet, dass keine zusätzlichen Verluste durch die Kabelkapazität
auftreten. Dadurch bleibt die Stromamplitude niedriger, was zu geringeren Übertragungsverlusten führt und
DC besonders für sehr lange Strecken attraktiv macht. In Abbildung 6 sind die Schaltzeichen der
verschiedenen Quellen dargestellt.
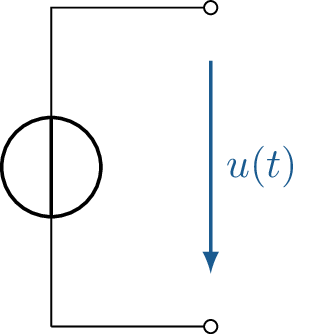
Spannungsquelle
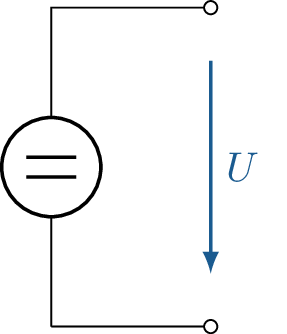
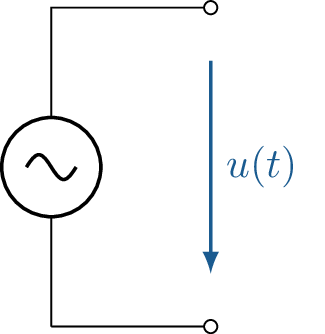
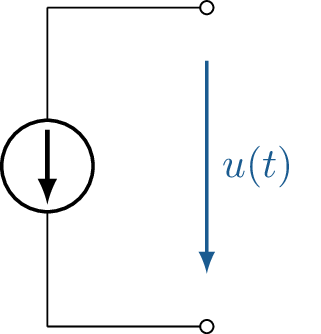
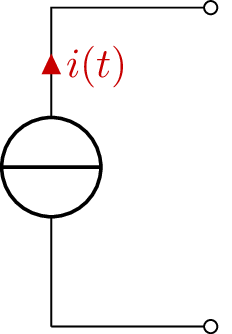
Stromquelle
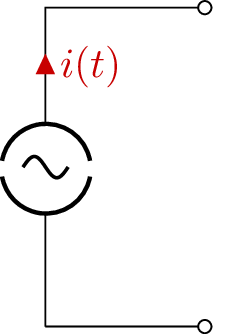
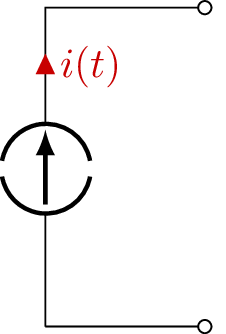
Es ist zu berücksichtigen, dass Wechselspannungs- und Stromquellen eine sinusförmige Ausgangsspannung bzw. einen sinusförmigen Ausgangsstrom haben, wohingegen die zeitlich beliebig veränderlichen Quellen jede beliebige Form haben können. Ein Beispiel dafür ist das Rechtecksignal, welches aus dem Ein- und Ausschalten einer Gleichspannungsquelle stammen könnte. Genutzt werden solche Quellen beispielsweise in der mobilen Anwendung der weit verbreiteten Bauart von Elektromotoren, welche auch Synchron, bzw. Asynchronmaschinen genannt werden. Diese Motoren werden in mobilen Anwendungen durch eine Gleichspannungsquelle betrieben, dessen Signalform mithilfe einer Leistungselektronik in das gewünschte Rechtecksignal gewandeln (gepulst) werden und im Motor durch über die Spulenwicklungen aus dem gepulsten Spannungssignal ein sinusförmigen Strom entsteht. Mehr dazu im Modul elektrische Maschinen. Ein weiteres Beispiel für zeitlich beliebige Signale ist die digitale Informationsübertragung in der Nachrichtentechnik, wobei eine Eins dem Highsignal und eine Null einem Lowsignal entspricht, was ebenfalls einem Rechtecksignal gleicht.