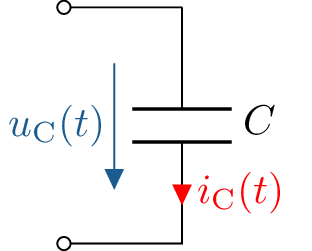Kapazität und Kondensator
In der Elektrotechnik gibt es drei grundlegende Komponenten, mit denen das elektrische Verhalten von Bauteilen beschrieben werden kann. Neben dem zuvor behandelten ohmschen Widerstand, gibt es noch die Kapazität und die Induktivität. In diesem Abschnitt geht es um die Eigenschaft der Kapazität, sowie dem dazugehörigen Bauteil, dem Kondensator. Der darauffolgende Abschnitt behandelt die Induktivität sowie das zugehörige Bauteil, die Spule.
Lernziele: Kapazität und Kondensator
Die Studierenden
- können zwischen Kapazität und Kondensator differenzieren.
- kennen die wichtigsten Parameter rund um den Kondensator und die Kapazität.
- können die Kapazität eines Kondensators berechnen.
1 Die elektrische Kapazität \(C\)
Die elektrische Kapazität ist die Fähigkeit eines Objektes, elektrische Energie in Form eines elektrischen Feldes, zu speichern. Diese Eigenschaft kommt zustande, sobald elektrische Ladungsträger ungleich verteilt sind und sich zwischen den Bereichen ein elektrisches Feld ausbildet. Das Formelzeichen der Kapazität ist \(C\) (capacity) während die Einheit in Farad (\(F\)) angegeben wird.
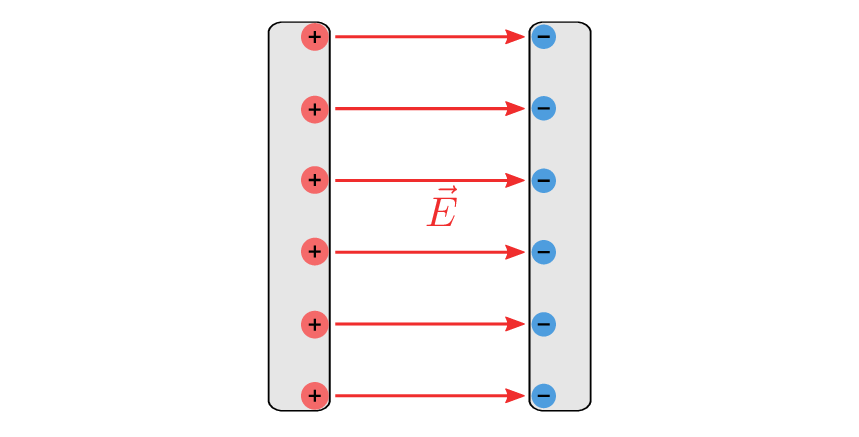
Das einfachste und geläufigste Beispiel, an dem die Kapazität erklärt werden kann, ist der Plattenkondensator. Bei dieser Art des Kondensators liegen sich zwei leitfähige Platten gegenüber, welche jeweils mit einem anderen Potential beaufschlagt werden. In Abbildung 1 ist ein Kondensator mit idealisiertem Feldverlauf dargestellt.
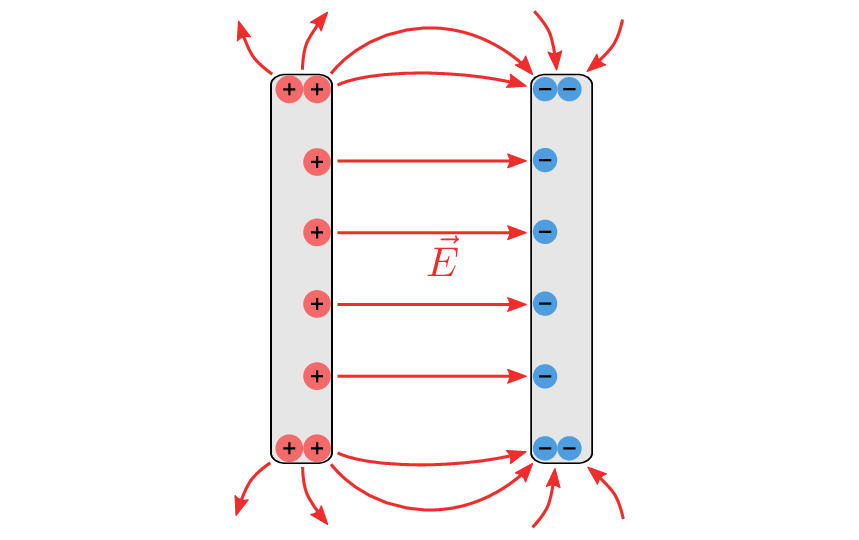
Aufgrund der unterschiedlichen Potentiale auf den Platten, bildet sich von der höheren zur geringer geladenen Platte ein elektrisches Feld aus. Im idealen Fall wird angenommen, dass sich außerhalb der Kondensatorplatten kein Feld ausbildet. In der Realität sammeln sich an den seitlichen Rändern der Platten ebenfalls Ladungsträger, welche zu komplizierteren Feldverteilungen führen. In Abbildung 2 ist die Grafik eines solchen realen Plattenkondensators dargestellt.
In vielen Fällen kann das reale Verhalten jedoch vernachlässigt werden, was die Berechnungen deutlich vereinfacht. Aus dem Grund wird im Folgenden nurnoch von idealisierten Kondensatoren ausgegangen.
Die Kapazität ist definiert als das Verhältnis der gespeicherten elektrischen Ladung \(Q\) zur angelegten Spannung \(U\). Je höher die Kapazität eines Kondensators ist, desto mehr Ladung kann er bei einer gegebenen Spannung speichern.
\begin {equation*} [C] = 1\, \text {Farad} = 1\, \text {F} = 1\,\, \frac {\text {C}}{\text {V}} = 1\, \frac {\text {A} \text {s}}{\text {V}} \label {eq:cqu_2} \end {equation*} \begin {equation} C = \frac {Q}{U} \end {equation} \begin {equation} Q = C \cdot U \Rightarrow C = \frac {Q}{U} = \frac {\varepsilon \cdot \iint \vec {E} \cdot \mathrm {d}\vec {A}}{\int \vec {E}\mathrm {d}\vec {s}} \label {eq:qcu2} \end {equation}
2 Der Kondensator als Bauelement
Die Eigenschaften der Kapazität werden in verschiedenen Bereichen der Elektrotechnik bewusst genutzt. Die Nutzbarmachung dieser Eigenschaften erfolgt mit Hilfe von Kondensatoren. Es gibt sie in verschiedenen Ausführungen. Abbildung 3 zeigt einige Beispiele von THT- bis hin zu SMD-Bauteilen.
Darüber hinaus gibt es sie aber auch in deutlich kleineren bzw. deutlich größeren Dimensionen. In der Hochfrequenztechnik werden Kapazitäten beispielsweise lediglich durch das Design der Leiterplatten realisiert, während Kondensatoren für industrielle oder enegietechnische Anwendungen mehrere Zentimeter bis Meter groß werden können.
Was alle Kondensatoren verbindet, ist ihre Fähigkeit, die Eigenschaft der Kapazität nutzbar zu machen, wie es im folgenden Schaltbild ?? dargestellt ist. Dieses Schaltbild repräsentiert jedoch nur die idealisierte, nutzbare Kapazität.
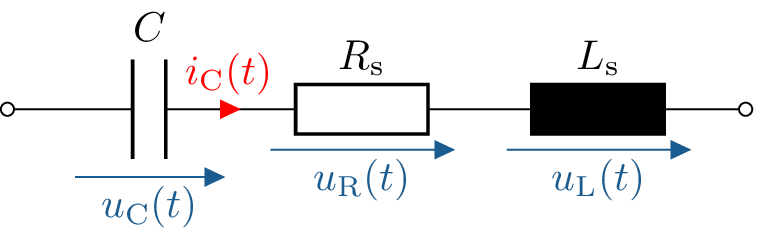
Für eine realitätsgetreue Nachbildung der Schaltung ist es wichtig den Kondensator als Bauteil vollständig zu beschreiben. Dies wird mit Hilfe eines Ersatzschaltbildes gemacht, welches auch die ungewollten, also parasitären Eigenschaften des Bauteils, nachbildet. Abbildung ?? zeigt ein solches Ersatzschaltbild.
Im Ersatzschaltbild des Kondensators werden nicht nur die nutzbare Kapazität, sondern auch die parasitären Eigenschaften berücksichtigt, die in realen Kondensatoren auftreten. Diese parasitären Eigenschaften entstehen beispielsweise durch die Induktivität der Anschlüsse und die ohmschen Verluste im Material. Das modellierte Ersatzschaltbild ermöglicht es, diese Effekte im Schaltungsentwurf zu berücksichtigen und das Schaltverhalten besser vorherzusagen.
Merke:
Der Kondensator ist der verzweifelte Versuch eine Kapazität nachzubilden.
3 Das Dielektrikum
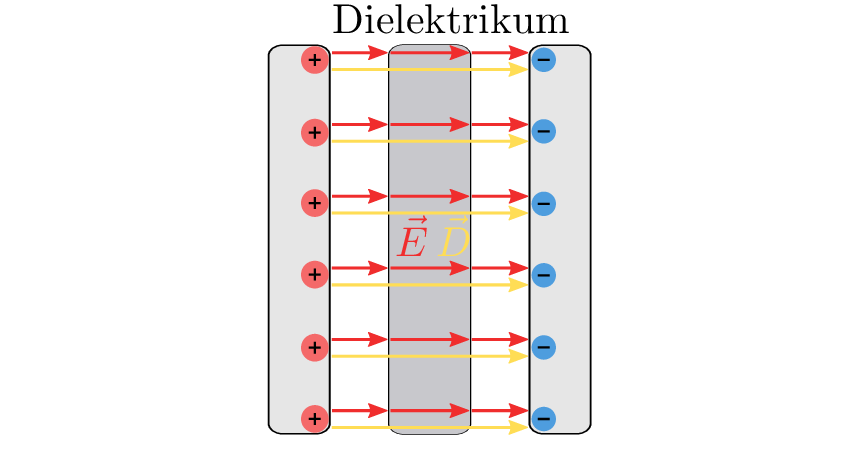
Das Dielektrium ist, wie der Name bereits impliziert, ein dielektrisches, also elektrisch nicht leitfähiges Material. Da jedes Material aus Atomen besteht und alle Atomrümpfe mit Elektronen versehen sind (Elektronenhülle), wirkt sich entsprechend auch ein elektrisch nicht leitfähiges Material auf das Verhalten des elektrischen Feldes aus. Sobald ein solches Material zwischen die Platten eines Kondensators eingefügt wird, ändern sich demnach auch die Eigenschaften des Kondensators. In Abbildung 6 ist anhand der unterbrochenen Pfeilung des elektrischen Feldes das unterschiedliche Verhalten zu erkennen. Die elektrische Flussdichte D ist eine Hilfsgröße, welche materialunabhängig ist, auf welche in Abschnitt 1.3.4 noch eingegangen wird.
Die Eigenschaften des Dielektrikums sind materialspezifisch und werden durch die Dielektrizitätszahl \(\varepsilon _\mathrm {r}\) quantifiziert. In Tabelle 1 sind Beispiele einiger Dielektrika und deren \(\varepsilon _\mathrm {r}\), aufgeführt:
| Material | \(\varepsilon _\mathrm {r}\) |
| Vakuum | 1 |
| Luft (bei STP) | 1.0006 |
| Kunststoff (PE) | 2.25-2.3 |
| Glas | 3-10 |
| Keramik | 5-300 |
| Silizium | 11.7 |
| Tantaloxid | 25-30 |
| Wasser | 81 |
Zur vollständigen Beschreibung der Materialeigenschaften des Dielektrikums wird neben der Dielektrizitätszahl noch die elektrische Feldkonstante \(\varepsilon _\mathrm {0}\) benötigt. Dabei handelt es sich um das dielektrische Verhalten des elektrischen Feldes im Vakuum. Während die Dielektrizitätszahl \(\varepsilon _\mathrm {r}\) einheitslos ist, bringt die elektrische Feldkonstante die Einheit \(\frac {\text {As}}{\text {Vm}}\) mit. Sie wird mit der relativen Dielektrizitätszahl multipliziert was zusammen die Dielektrizitätskonstante \(\varepsilon \) ergibt.
\begin {equation*} [\boldsymbol \varepsilon ] = 1\,\frac {\text {Farad}}{\text {m}} = 1\, \frac {\text {F}}{\text {m}} = 1\, \frac {\text {As}}{\text {Vm}} \end {equation*} \begin {equation} \boldsymbol \varepsilon = \boldsymbol \varepsilon _\mathrm {0} \cdot \boldsymbol \varepsilon _\mathrm {r} \end {equation} \begin {align*} \boldsymbol \varepsilon & : \text {Dielektrizitätskonstante} \\ \boldsymbol \varepsilon _\mathrm {0} & : \text {Elektrische Feldkonstante (8.85421878 $\cdot $ 10}^{-12}) \\ \boldsymbol \varepsilon _\mathrm {r} & : \text {Relative Dielektrizitätszahl} \\ \end {align*}
Mit Hilfe dieser Materialeigenschaften des Dielektrikums und den Dimensionen sowie der Entfernung der Kondensatorplatten, kann die Kapazität des Kondensators wie folgt berechnet werden: \begin {equation*} [C] = 1\,\text {F} \end {equation*} \begin {equation} C = \frac {\boldsymbol \varepsilon \cdot A}{d} \end {equation} \begin {align*} A & : \text {Querschnittsfläche des Materials } (\text {m}{^2}) \\ d & : \text {Abstand der Elektroden (\text {m})} \end {align*}
4 Die elektrische Flussdichte
Die elektrische Flussdichte \(\vec {D}\), auch Verschiebungsdichte genannt, steht proportional zum elektrischen Feld \(\vec {E}\). Ihr Vorteil besteht darin, dass sie materialunabhängig ist, was mathematische Vorteile mit sich bringt.
\begin {equation} \vec {D} = \boldsymbol \varepsilon \cdot \vec {E} + P \end {equation}
Zusätzlich zur Dielektrizitätskonstanten \(\varepsilon \) wird die Polarisation des Mediums \(P\) addiert. Sie beschreibt das Polarisationsverhalten, welches im Einschaltvorgang abläuft. Im statischen Fall kann die Polarisation \(P\) oft vernachlässigt werden, was die Gleichung wie folgt vereinfacht.
\begin {equation*} [D] = 1\,\frac {\text {Coulomb}}{\text {m}^2} = 1\,\frac {\text {C}}{\text {m}^2} = 1\,\frac {\text {As}}{\text {m}^2} \end {equation*} \begin {equation} \vec {D} = \boldsymbol \varepsilon \cdot \vec {E} \end {equation}
Einführung in die zeitabhängige Vorgänge
Bisher ist bekannt, dass elektrische Felder in leitfähigen Materialien einen Strom \(I\) und eine Spannung \(U\) verursachen. Der Strom \(I\) und die Spannung \(U\) beschreiben die Felder jedoch nur integral, sie werden also als zeitlich konstant angesehen. Im Gegensatz zum Widerstand \(R\) gibt es jedoch Bauteile (Kondensatoren und Spulen), die ein zeitlich veränderliches Verhalten aufweisen. Der ohm’sche Widerstand \(R\) alleine reicht somit nicht aus, um die Verhältnisse bei Netzwerken mit zeitlich veränderlichen Vorgängen zu beschreiben. Zur Beschreibung dieser zeitabhängigen Verhalten werden die zeitabhängigen Größen \(u(t)\) und \(i(t)\) verwendet.
Die Herleitung der Zeitabhängigkeiten kann mathematisch folgendermaßen gezeigt werden. Aus der Formel ?? ist bereits die Grundgleichung des Kondensators bekannt:
\begin {equation} Q = C \cdot U \label {eq:qcu} \end {equation} Zur Beschreibung des zeitlichen Verhaltens des Kondensators, wird die Änderung der Ladung über die Zeit betrachtet
\begin {equation} \frac {\mathrm {d}Q}{\mathrm {d}t} = C \cdot \frac {\mathrm {d}U}{\mathrm {d}t} \end {equation}
\(\frac {\mathrm {d}Q}{\mathrm {d}t}\) beschreibt die Änderungsrate der Ladung, welche nach dem Grundgesetz der Elektrotechnik dem Strom \(i(t)\) entspricht, der in den Kondensator hinein- oder herausfließt.
\begin {equation} \frac {\mathrm {d}Q}{\mathrm {d}t} = i(t) \end {equation}
Wird nun in der Formel 7 die konstante Ladung Q durch die zeitlich veränderliche Größe \(i(t)\) ersetzt, erhält auch die Spannung eine zeitliche Abhängigkeit.
\begin {equation} i_\mathrm {c}(t) = C \cdot \frac {\mathrm {d}u_\mathrm {c}(t)}{\mathrm {d}t} \label {eq:ict} \end {equation}
Durch mathematische Umstellung nach \(u_\mathrm {c}(t)\) kann die Spannung in Abhängigkeit des Stromes und der Kapazität dargestellt werden:
\begin {equation} u_\mathrm {c}(t) = \frac {1}{C} \cdot \int i_\mathrm {c}(t) \mathrm {d}t \label {eq:uci} \end {equation}
Aus der Gleichung 10 folgt unmittelbar, dass sich die Spannung an einer Kapazität nicht schlagartig ändern kann, da dafür ein unendlich hoher Strom erforderlich wäre.
5 Schaltverhalten eines Kondensators
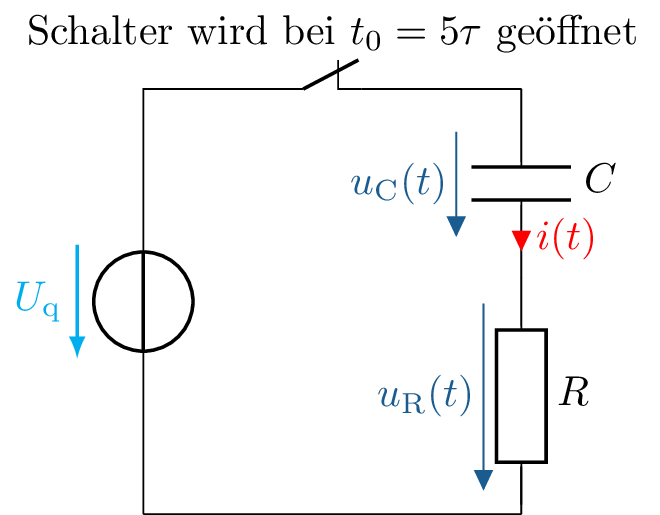
Das Schaltverhalten beschreibt das Verhalten eines Bauteils bei Änderung der angelegten Spannung. Je nachdem ob eine Spannungsquelle ein- oder ausgeschaltet wird, verhalten sich Strom und Spannung am Bauteil entsprechend seiner Charakteristika. Zur Analyse des zeitlichen Verhaltens von Bauteilen ist zuerst ein Schaltbild notwendig, welches die zu analysierende Schaltung visualisiert. Abbildung 6a zeigt ein Schaltbild einer Reihenschaltung einer Kapazität \(C\) mit einem Widerstand \(R\), welche über einen Schalter mit einer Spannung \(U_\mathrm {q}\) versorgt werden können.
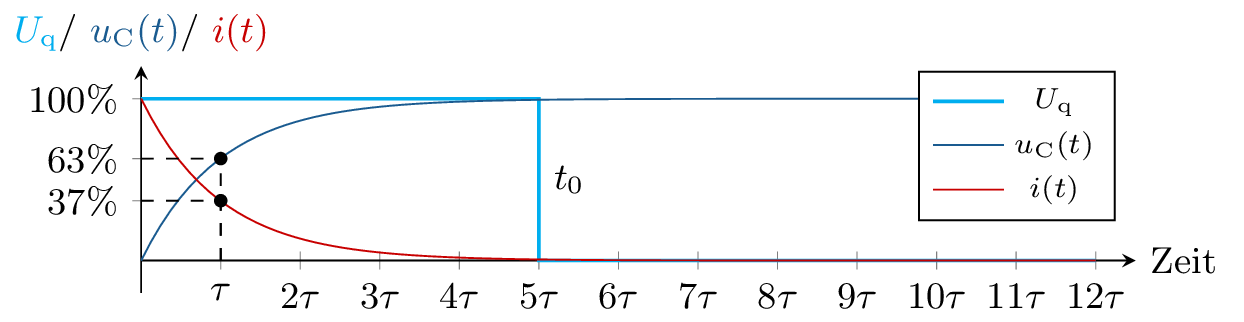
Im Diagramm 6b ist zu sehen, dass sich trotz angelegter Gleichspannung \(U_\mathrm {q}\) die Spannung \(u_\mathrm {c}(t)\) zeitgleich nicht mitändert, sondern eine Trägheit aufweisen. Dieses zeitlich veränderliche Verhalten wird im Schaltbild 6a durch die zeitabhängigen Größen \(u(t)\) und \(i(t)\) ausgedrückt.
In diesem Beispiel ist der Schalter zu Beginn geschlossen und wird bei \(t_\mathrm {0} = 5\tau \) geöffnet. Der Kondensator ist anfangs nicht geladen. Im Diagramm ist zu erkennen, dass sich trotzt angelegter Spannung \(U_\mathrm {q}\) die Spannung über der Kapazität \(u_\mathrm {C}(t)\) nicht sprunghaft ändert.
Dieses Einschaltverhalten resultiert aus der Aufladung der Kapazität. Die Ladungsträger müssen sich dafür auf den Kondensatorplatten ansammeln. Dies geschieht so lange, bis die Spannung zwischen den Platten der angelegten Spannung der Spannungsquelle entspricht. Da die zur Aufladung benötigten Ladungsträger in die Kondensatorplatten wandern müssen, fließt während dieses Vorgangs ein entsprechender Strom \(i_\mathrm {C}(t)\).
Im Fall einer ideal leitenden Schaltung ohne ohm’schen Widerstand, würden sich die Ladungsträger unendlich schnell auf den Kondensatorplatten ansammeln, was einem unendlich hohen Strom entsprechen würde. Im realen Fall hat der Kondensator bzw. die Hinleitung zum Kondensator, einen ohm’schen Widerstand, welcher die Ladungsträger auf dem Weg zu den Kondensatorplatten ausbremst, also die elektrische Stromstärke reduziert. Daraus folgt der maximal mögliche Strom \(I_\mathrm {max}\).
\begin {equation} I_\mathrm {max} = \frac {U_\mathrm {q}}{R} \end {equation}
Sobald der Schalter geöffnet wird, bleibt die Spannung über der Kapazität erhalten. Dies bedeutet, dass die zugeführte Energie in der Kapazität verbleibt und sich im stationären Fall nicht mehr ändert. Dementsprechend fließt bei einer aufgeladenen Kapazität auch kein Strom mehr, was in einem eingeschwungenen Gleichstromnetzwerk einem Leerlauf gleichzusetzen ist.
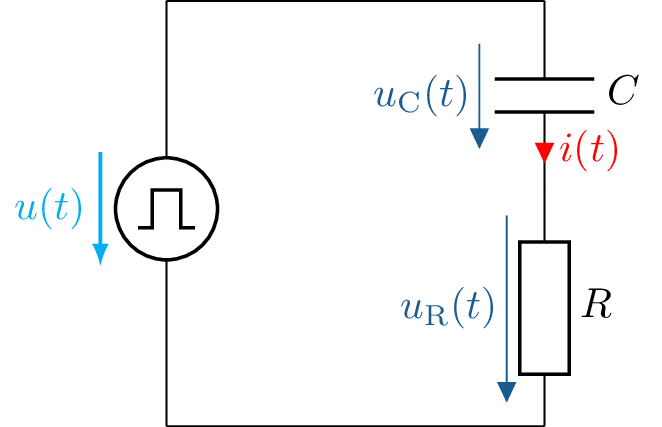
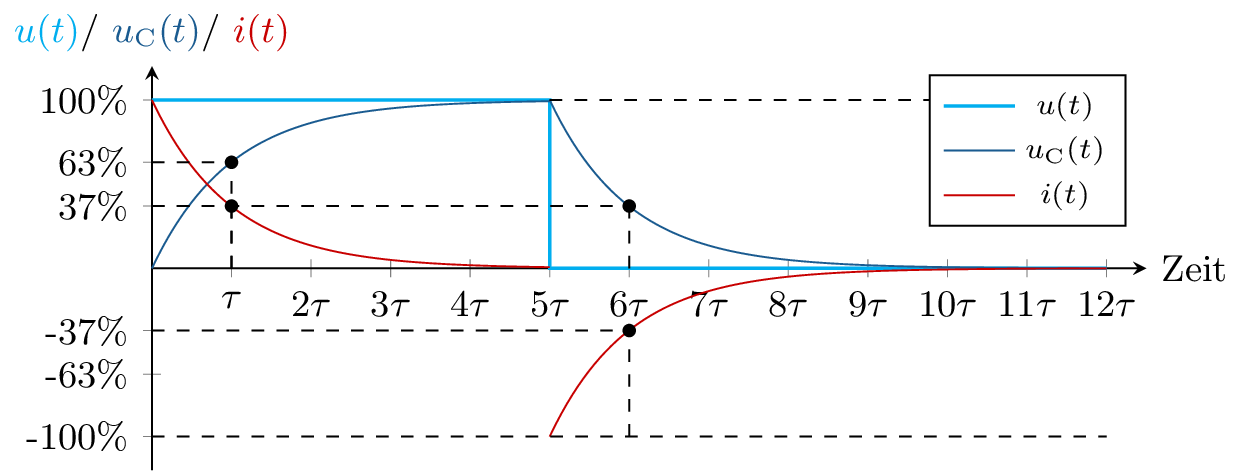
Mit Hilfe der beiden Formeln 10 und 11 ist das Verhalten von Strom und Spannung an einer Kapazität vollständig beschrieben, was nun diverse Berechnungen ermöglicht. Ein weiteres Beispiel ist das Schaltverhalten einer Kapazität bei anlegen einer Rechteckspannung. Der Unterschied besteht darin, dass nicht wie in Beispiel 6a, eine konstante Spannungsquelle über einen Schalter geschaltet wird, sondern die Spannungsquelle selbst die Eingangsspannung bestimmt.
Im Gegensatz zum Schalter, versucht die Spannungsquelle im Beispiel 7a ab dem Zeitpunkt \(t_\mathrm {0} = 5\tau \) die Systemspannung auf \(0\) zu ziehen. Dies führt dazu, dass die Kapazität entladen wird. Dies führt entsprechend zu einem entgegengesetzten Stromfluss \(i_\mathrm {C}(t)\), da sich die Ladungsträger von den Kondensatorplatten wegbewegen, um wieder einen neutralen Zustand zu erreichen.
Beispiel 1: Berechnungs der Kapazität
- Ladung auf Platten \(Q = \sigma \cdot A = \varepsilon \cdot E \cdot A\)
- Kapazität mit \(C = \frac {\varepsilon \cdot A}{d}\) berechnen
- Gespeicherte Energie \(W = \frac {1}{2} \cdot C \cdot U^2 \)
- Kapazität zweier Kondensatoren mit verschiedenen \(\varepsilon _{\mathrm {r}}\) über \(\vec {D}\) berechnen