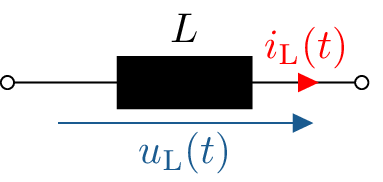Induktivität und Spule
Das Gegenstück zum Kondensator ist die Spule, oder genauer gesagt: Das Gegenstück zur Kapazität \(C\) ist die Induktivität \(L\). Die Induktivität ist ebenfalls ein Energiespeicher, wobei der Unterschied in der Art der genutzten Felder liegt. Während bei der Kapazität die Energie in Form eines elektrischen Feldes gespeichert wird, geschieht dies bei der Induktivität über das magnetische Feld.
Lernziele: Induktivität und Spule
Die Studierenden
- können zwischen Induktivität und Spule differenzieren.
- kennen die wichtigsten Parameter rund um die Induktivität und die Spule.
- können die Induktivität einer Spule berechnen.
1 Die Induktivität \(L\)
Die Induktivität ist die Fähigkeit eines Objektes, elektrische Energie in Form eines magnetischen Feldes zu speichern. Diese Eigenschaft kommt zustande, sobald ein elektrischer Strom durch einen Leiter fließt um welchen sich entsprechend ein magnetisches Feld ausbildet. Das Formelzeichen der Induktivität ist \(L\) (benannt nach dem französischen Physiker Heinrich Lenz), während die Einheit in Henry (\(\mathrm {H}\)) angegeben wird.
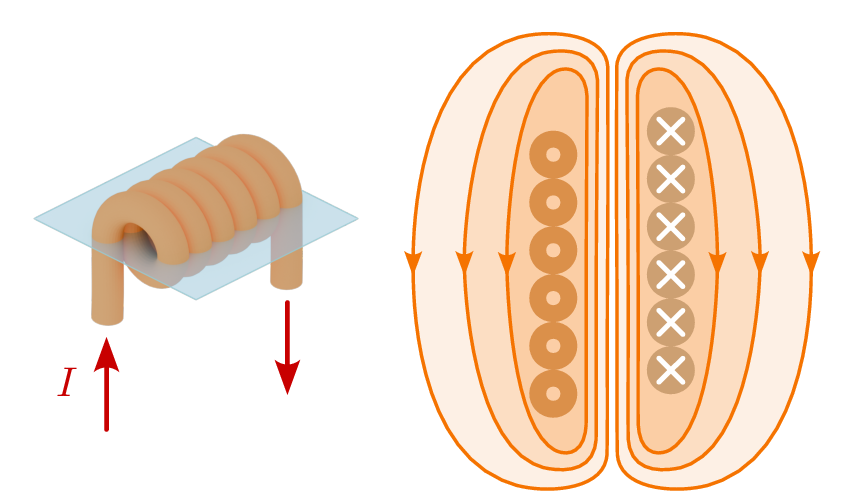
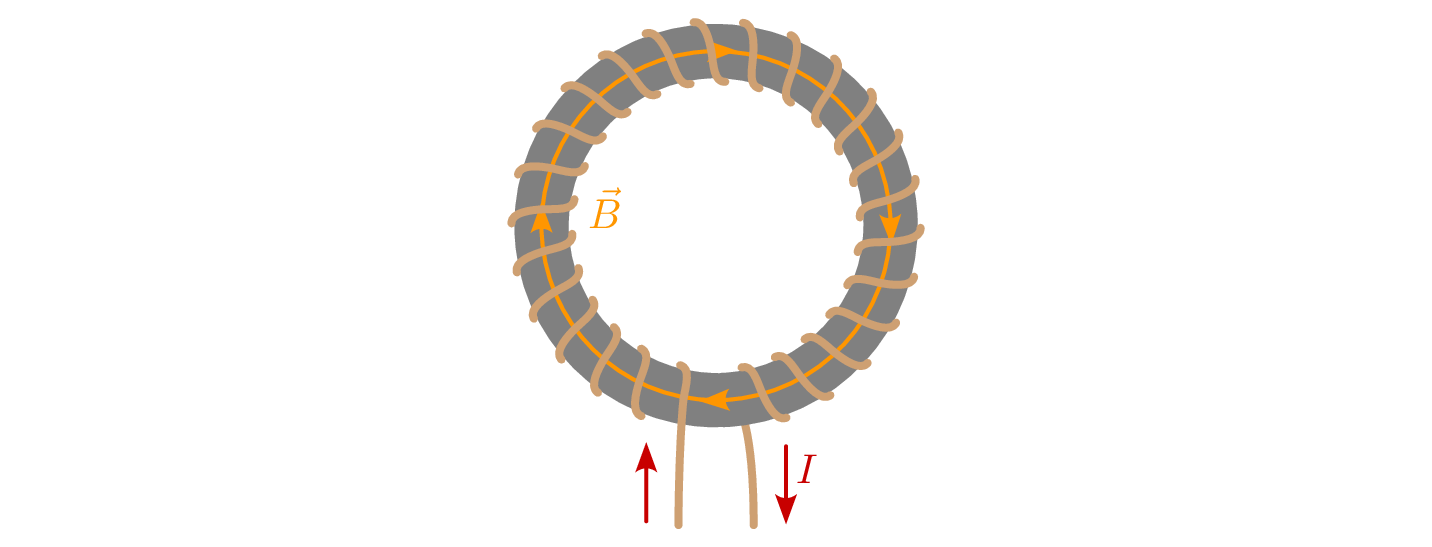
Das einfachste und geläufigste Beispiel, an dem die Induktivität erklärt werden kann, ist die Spule. Obwohl sich das Phänomen der Induktivität bereits bei einem einfachen Leiter ausbildet, wird dieser Effekt durch den Aufbau einer Spule bewusst verstärkt. In Abbildung 1 ist ein Zylinderluftspule mit ihrer magnetischen Flussdichte \(\vec {B}\) dargestellt.
Das Thema der magnetischen Größen wird ausführlich in Modul 6 behandelt. Zum Verständnis der Funktionsweise einer Spule und der daraus resultierenden Induktivität, soll eine kurze Einführung zur Entstehung von Magnetismus helfen.
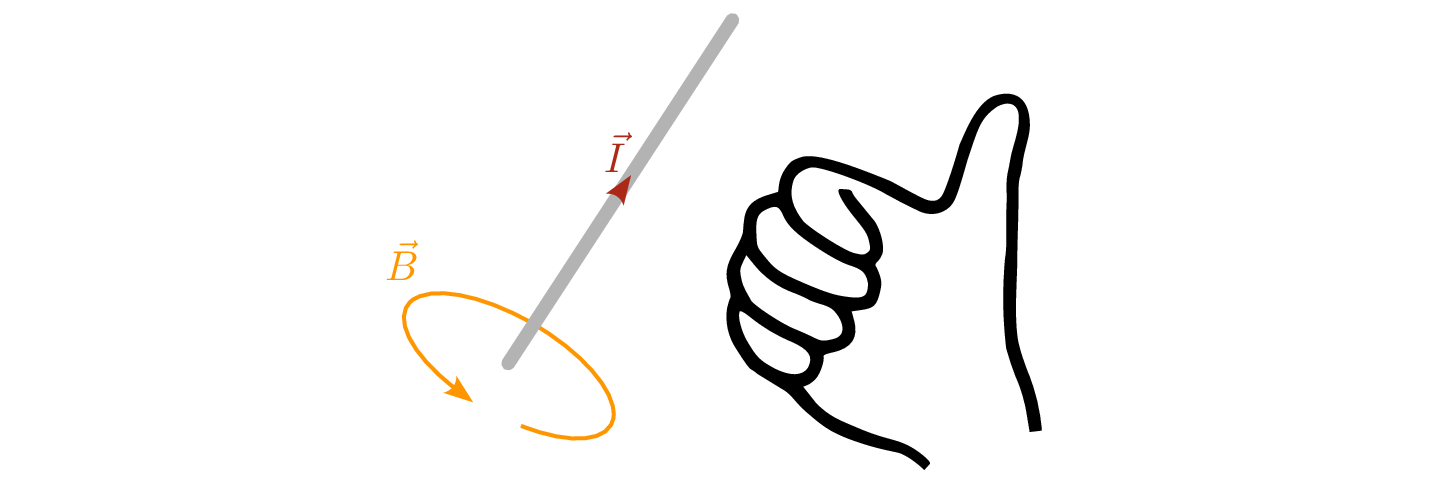
Sobald Strom durch einen geraden Leiter fließt, entsteht ein magnetisches Feld konzentrisch um den Leiter herum. Abhängig von Stromstärke und Stromrichtung ändert sich auch das magnetische Feld. Die Rechte-Faust-Regel dient dabei als Gedankenstütze zur Bestimmung der Richtung und Orientierung des Magnetfeldes.
Entsprechend der Grafik 2 verläuft das Magnetfeld in Richtung der Fingerspitzen konzentrisch um den Leiter herum, sofern man den Daumen in Richtung der technischen Stromrichtung, also entgegen der Fließrichtung der Elektronen, ausrichtet. Das Magnetfeld dreht sich von Süd nach Nord und hat eine Flussdichte \(\vec {B}\), sowie eine Feldstärke \(\vec {H}\). Dabei ist zu beachten, dass sich die magnetische Flussdichte \(\vec {B}\) analog zur elektrischen Feldstärke \(\vec {E}\) , und die magnetische Feldstärke \(\vec {H}\) analog zur elektrischen Flussdiche \(\vec {D}\), verhält. Im Modul 6 wird das Thema Magnetismus ausführlicher behandelt. In diesem Modul geht es primär um das Kennenlernen der Spule und der Induktivität.
Der britische Physiker und Chemiker Michael Faraday führte mitte des 19. Jahrhunderts Experimente durch, bei denen er eine Spule in der Nähe eines Magneten bewegte oder den Strom in einer benachbarten Spule veränderte. Dabei stellte er fest, dass sich die Größe der induzierten Spannung proportional zur Änderungsrate des Magnetfeldes verhält.
\begin {equation} U_\mathrm {i} \sim \frac {\mathrm {d}\phi }{\mathrm {d}t} \end {equation}
Faraday stellte fest, dass der Proportionalitätsfaktor von der Anzahl der Wicklungen der Spule abhängt.
\begin {equation} U_\mathrm {i}= -N \cdot \frac {\mathrm {d}\phi }{\mathrm {d}t} \end {equation}
Etwa zur gleichen Zeit entdeckte der amerikanische Physiker Joseph Henry das Phänomen der Selbstinduktion, wobei ein elektrischer Strom in einer Spule eine Spannung in der Spule selbst induzieren kann, wenn der Strom verändert wird. Auch hier wurde ein proportionales Verhalten festgestellt.
\begin {equation} U_\mathrm {i} \sim \frac {\mathrm {d}I}{\mathrm {d}t} \end {equation}
Diese Eigenschaft der Spule die durch das Speichern magnetischer Energie entsteht ist die Induktivität \(L\), deren Einheit dem Physiker zu Ehren als Henry \([\mathrm {H}]\) benannt wurde.
\begin {equation} U_\mathrm {i}= -L \cdot \frac {\mathrm {d}I}{\mathrm {d}t} \end {equation}
Das Minus-Zeichen kommt daher, dass der induzierte Strom nach der Lenz’schen Regel seiner Ursache entgegenwirkt.
Analog zum Kondensator, kann auch das zeitabhängige Verhalten für die Spule folgendermaßen ausgedrückt werden:
Spannung über der Induktivität \begin {equation} u_\mathrm {L}(t) = L \cdot \frac {di_\mathrm {L}(t)}{dt} \end {equation} Strom durch die Induktivität \begin {equation} i_\mathrm {L}(t) = \frac {1}{L} \cdot \int u_\mathrm {L}(t) \, dt \end {equation}
2 Die Spule als Bauelement
Mit dem Wissen über das magnetische Feld kann nun der Aufbau und die Funktionsweise der Spule erklärt werden. Ein einfaches Beispiel dafür ist die Zylinderluftspule. Wird ein Leiter zu einer Leiterschleife geformt, bildet sich das Magnetfeld so aus, dass es durch die Schleifenöffnung hindurchgeht. Werden nun mehrere Leiterschleifen hintereinander gewickelt, wird das Magnetfeld um den Faktor der Windungszahl verstärkt. Diese Anordnung von gewickelten Leiterschleifen ergibt die in Abbildung 3 gezeigte Zylinderluftspule.
Ihren Namen verdankt diese Spule ihrer zylindrischen Form in Längsrichtung und des Mediums Luft im
inneren ihrer Wicklungen. Wenn nun ein Strom durch die Spule fließt, überlagern sich die Magnetfelder der
einzelnen Wicklungen zu einem stärkeren Magnetfeld. Die Stärke hängt dabei von der Windungszahl und
der Stromstärke, sowie der Entfernung zum Leiter, ab. Je nach Orientierung des Stromes und der
Wicklungen, entsteht bei einer Zylinderluftspule auf der einen Seite ein Nord- und auf der anderen Seite ein
Südpol. Der Verlauf der Magnetfeldlinien in einer Zylinderluftspule entspricht der Abbildung 1.
Was alle Spulen verbindet, ist ihre Fähigkeit, die Eigenschaft der Induktivität nutzbar zu machen, wie es im folgenden Schaltbild 5 dargestellt ist. Dieses Schaltbild repräsentiert jedoch nur die idealisierte, nutzbare Induktivität.
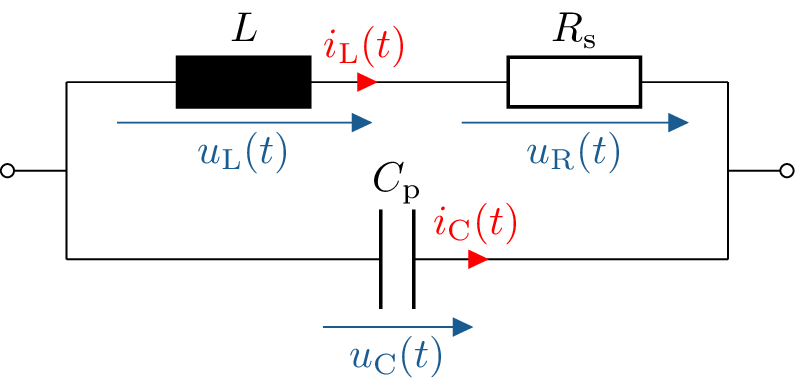
Für eine realitätsgetreue Nachbildung der Schaltung ist es wichtig die Spule als Bauteil vollständig zu beschreiben. Dies wird mit Hilfe eines Ersatzschaltbildes gemacht, welches auch die ungewollten, also parasitären Eigenschaften des Bauteils, nachbildet. Abbildung 6 zeigt ein solches Ersatzschaltbild.
Im Ersatzschaltbild einer Spule werden nicht nur die nutzbare Induktivität, sondern auch die parasitären Eigenschaften berücksichtigt, die in realen Spulen auftreten. Diese parasitären Eigenschaften entstehen beispielsweise durch die Kapazitäten zwischen den Wicklungen und die ohmschen Ver- luste im Material. Das modellierte Ersatzschaltbild ermöglicht es, diese Effekte im Schaltungsentwurf zu berücksichtigen und das Schaltverhalten besser vorherzusagen.
Merke:
Die Spule ist der verzweifelte Versuch, eine Induktivität nachzubilden.
3 Die Permeabilität
Ähnlich wie im Fall des Kondensators und der Kapazität, unterscheidet sich auch die Stärke des Magnetfeldes abhängig vom Material. Was beim Kondensator das Dielektrikum und die Permitivität sind, wird bei der Spule als ferromagnetisches Material und Permeabilität bezeichnet. Ein Beispiel einer Spule mit einem ferromagnetischen Material ist die Ringkernspule 7.
Bei der Ringkernspule handelt es sich um einen mit Draht umwickelten Ferritring. Innerhalb des Materials findet eine Ausrichtung auf atomarer Ebene statt, was zu einer Verstärkung des Magnetfeldes führt. Die Stärke der magnetischen Flussdichte \(\vec {B}\) wird dabei neben der Dimensionen und der Stromstärke, von den Materialeigenschaften, insbesondere von der Permeabilität, bestimmt.
Die folgende Tabelle 1 zeigt die Permeabilitätszahl einiger gängiger Materialien:
| Material | \(\mu _\mathrm {r}\) |
| Supraleiter 1. Art | \(0\) |
| Vakuum | \(1\) |
| Luft (bei STP) | \(1.00000037\) |
| Kupfer | \(0.999994\) |
| Gold | \(0.999964\) |
| Aluminium | \(1.000022\) |
| Eisen | \(300-10000\) |
| Ferrit | \(4-15000\) |
Zur vollständigen Beschreibung der Eigenschaften des ferromagnetischen Materials wird neben der Permeabilitätszahl noch die magnetische Feldkonstante \(\mu _0\) benötigt. Dabei handelt es sich um das Verhalten des magnetische Feldes im Vakuum. Während die Permeabilitätszahl \(\mu _r\) einheitslos ist, bringt die magnetische Feldkonstante die Einheit \(\mathrm {H/m}\) mit. Sie wird mit der relativen Permeabilität des Materials multipliziert was zusammen die Permeabilitätskonstante \(\mu \) ergibt.
\begin {equation*} [\mu ] = 1\, \frac {\text {Henry}}{\text {m}} = 1\, \frac {\text {H}}{\text {m}} = 1\, \frac {\text {Vs}}{\text {Am}} \end {equation*} \begin {equation} \mu = \mu _\mathrm {r} \cdot \mu _\mathrm {0} \end {equation}
\begin {align*} \mu & : \text {Permeabilitätskonstante} \\ \mu _\mathrm {0} & : \text {Magnetische Feldkonstante ($\approx 4\pi \cdot 10^{-7}$)} \\ \mu _\mathrm {r} & : \text {Relative Permeabilitätszahl} \\ \end {align*}
Mit Hilfe der Permeabilität, des Stromes, der Windungszahl und der Länge der Spule, kann die magnetische Flussdichte \(\vec {B}\) mit der Einheit Tesla \(\mathrm {T}\) berechnet werden.
\begin {equation} \vec {B} = \mu \cdot \vec {H} \end {equation}
\begin {align*} [B] = \frac {\text {H/m} \cdot \text {A} \cdot 1}{\text {m}} = \frac {\text {H} \cdot \text {A}}{\text {m}^2} = \frac {(\text {V} \cdot \text {s / } \cancel {\text {A}}) \cdot \cancel {\text {A}}}{\text {m}^2} = \frac {\text {V} \cdot \text {s}}{\text {m}^2} = \text {T (Tesla)} \end {align*}
\begin {equation} B = \frac {\mu \cdot I \cdot N} {l} \end {equation}
\begin {align*} \mu & : \text {Permeabilitätskonstante} \\ I & : \text {Elektrische Stromstärke} \\ N & : \text {Anzahl der Windungen} \\ l & : \text {Länge des Magnetkreises} \end {align*}
Die Induktivität selbst hängt ebenfalls von der Bauform und den verwendeten Materialien ab. \begin {equation*} [L] = 1\, \text {Henry} = 1\, \text {H} = 1\, \frac {\text {Vs}} {\text {A}} \end {equation*} \begin {equation} L = \frac {\mu \cdot N^2 \cdot A}{l} \end {equation}
4 Die magnetische Feldstärke
\begin {equation} \vec {B} = \mu \cdot \vec {H} \end {equation}
5 Schaltverhalten einer Spule
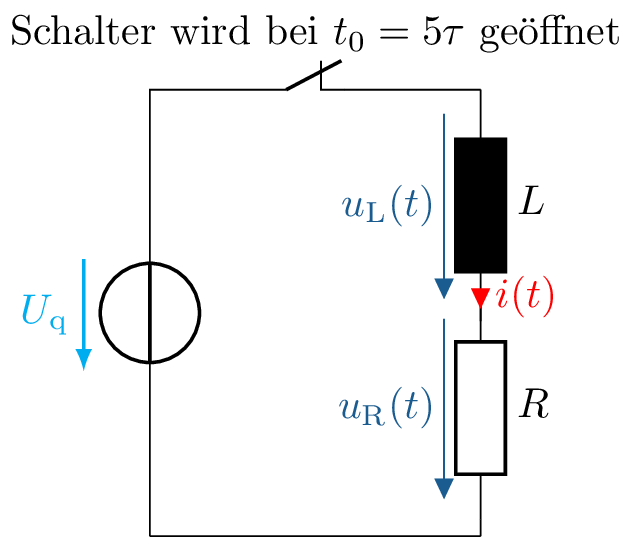
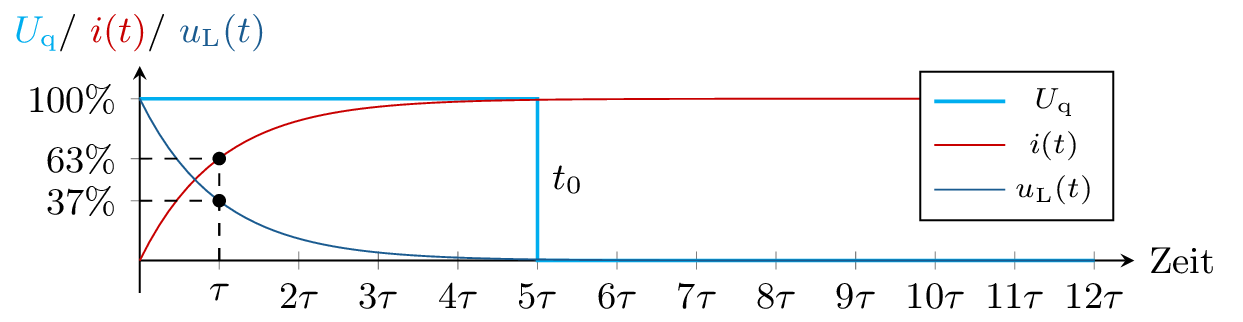
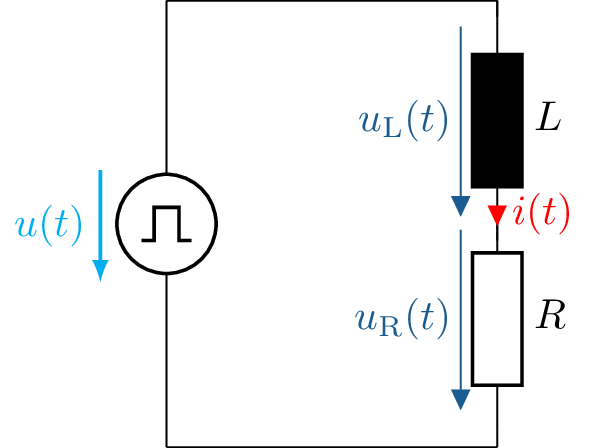
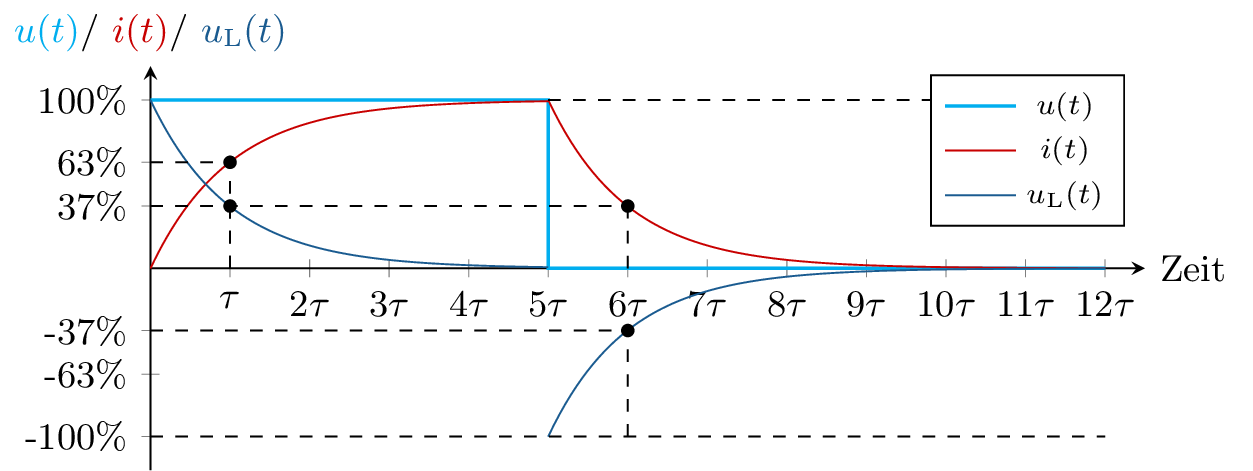
Zum besseren Verständnis der Funktion einer Spule wird nun ein zeitlich veränderliches Signal, hier der Einschalt- und Ausschaltvorgang, betrachtet. Das grundlegende Prinzip der Induktivität basiert darauf, dass ein zeitlich veränderlicher Strom ein zeitlich veränderliches Magnetfeld erzeugt. Dieses zeitlich veränderliche Magnetfeld induziert wiederum einen Induktionsstrom in die Spule selbst. Aufgrund der Lenz’schen Regel wirkt der Induktionsstrom jedoch entgegen seiner Ursache, was einen sprunghaften Anstieg des Stromes verhindert.
In der praktischen Anwendung ermöglicht die Induktivität die Konstruktion von Komponenten wie Transformatoren, Drosseln und Induktivitäten, die in einer Vielzahl von elektrischen und elektronischen Geräten zu finden sind. Von der Filterung von Signalen über die Energieübertragung bis hin zur Steuerung elektromagnetischer Interferenzen ist die Induktivität ein Schlüsselelement in der modernen Elektrotechnik.
Beispiel 1: Berechnungs der Induktivität
- Berechnung der Induktivität \(L\)
- Berechnung der magnetischen Flussdichte \(\vec {B}\)
- Gespeicherte Energie im Magnetfeld \(E_\mathrm {m}\) ?