Sprache wählen Icon

Superpositionsprinzip

Nach der grundsätzlichen Analyse von Maschen und Knoten in elektrischen Netzwerken werden folgend zunehmend kompliziertere elektrische Netzwerke betrachtet. Hierzu wird das Überlagerungsverfahren nach Helmholtz verwendet. Das Überlagerungsverfahren wird auch als Superpositionsprinzip bezeichnet. Beim Superpositionsprinzip werden nacheinander alle Quellen einzeln ausgewertet und die Ergebnisse der einzelnen Berechnungen überlagert.

Lernziele: Superpositionsprinzip

Die Studierenden

  • verstehen die Bedingungen der Systemtheorie für die Analyse von Gleichstromnetzwerken.
  • können den Überlagerungssatz (das Superpositionsprinzip) auf elektrische Netzwerke anwenden.

1 Exkurs Systemtheorie

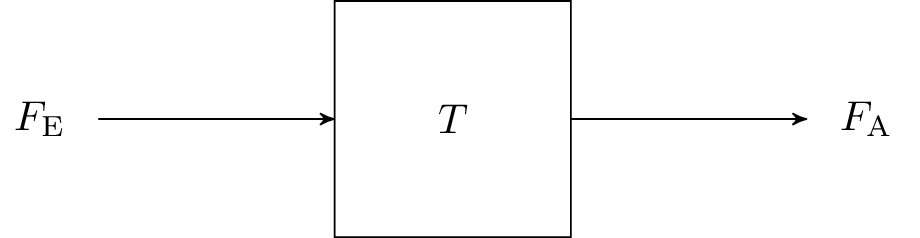
Wird in einem Modell lediglich das Einganssignal und das Ausgangssignal betrachtet, wird von einer Blackbox gesprochen. Hier ist keinerlei Information darüber gegeben, was zwischen diesen beiden Signalen passiert. Die Abbildung 1 beschreibt so ein Modell. Hier wird eine Black Box betrachtet, welche als Eingansgröße \(F_\mathrm {E}\) und als Ausgangsgröße \(F_\mathrm {A}\) aufweist. In der Blackbox wird das Eingangssignal in das Ausgangssignal transformiert. Das Bildnis insgesamt wird als System bezeichnet.

Die Grafik zeigt ein Blockdiagramm mit einem einzelnen rechteckigen Block T in der Mitte. Links führt ein waagerechter Pfeil mit der Bezeichnung F˙E(Eingangsgröße) auf den Block zu, rechts verlässt ihn ein Pfeil mit der Bezeichnung F˙A(Ausgangsgröße). Der Block T steht damit für ein System welches transformiert werden soll, dass die Eingangsgröße F˙E in die Ausgangsgröße F˙A überführt.

Abbildung 1: Blackbox in der Systemtheorie. Eine Blackbox mit linksseitiger Eingangsgröße und rechtsseitiger Ausgangsgrößen.

Ausgehend von der vorgestellten Blackbox lässt sich das Ausgangssignal \(F_\mathrm {A}\) in der Abhängigkeit des Eingangssignals \(F_\mathrm {E}\) bestimmen. Diese Transformation lässt sich durch die Gleichung 1 beschreiben.

\begin {equation} F_\mathrm {A}=T(F_\mathrm {E}) \label {GleichungFunktionSystem} \end {equation}

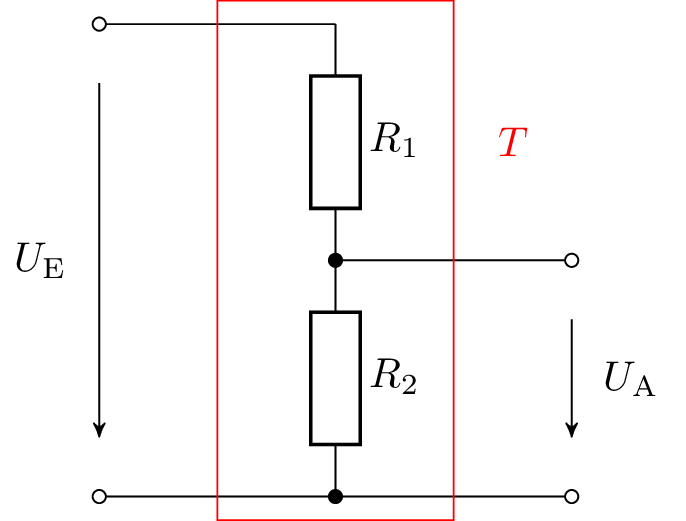
Ein elektrisches Netzwerk kann auch als solch ein System betrachtet werden. Das in der Abbildung 2 dargestellte elektrische Netzwerk verfügt über eine Eingangsspannung \(U_\mathrm {E}\) als Eingangsgröße und eine Ausgangsspannung \(U_\mathrm {A}\) als Ausgangsgröße. Die Blackbox, welche das zu transformierende System abbildet, setzt sich aus den beiden Widerständen \(R_1\) und \(R_2\) zusammen.

Die Schaltung zeigt ein Zweipol-Netzwerk T als einfachen Spannungsteiler aus zwei in Serie geschalteten Widerständen R˙1(oben) und R˙2(unten). Zwischen den oberen und unteren Anschlussklemmen liegt die Eingangsspannung U˙Ein in vertikaler Richtung an. Am Verbindungsknoten zwischen R˙1 und R˙2 wird die Ausgangsspannung U˙A nach rechts abgegriffen.

Abbildung 2: Spannungsteiler als Blackbox. Betrachtung eines elektrischen Netzwerkes als Blackbox mit Eingangsspannung und Ausgangsspannung.

Der Zusammenhang der Abhänigkeit des Ausgangssignals eines Systems vom Eingangssignal aus Gleichung 1 gilt weiterhin. Das Ausgangssignal lässt sich als Transformation des Eingangssignales wie in der Gleichung 2 beschreiben. Das Ausgangssignal ist gleich der Spannung, welche über dem Widerstand \(R_2\) abfällt. Diese Spannung lässt sich aus dem Produkt der Eingangsspannung und dem Widerstandsverhältnis berechnen. Dieser Zusammenhang wurde auch bereits beim Spannungsteiler im Kapitel 4 behandelt.

\begin {equation} U_\mathrm {A}=T(U_\mathrm {E})=U_\mathrm {E}\cdot \frac {R_2}{R_1+R_2} \label {GleichungNetzwerk} \end {equation}

Kausalität

Beruht eine Ausgangsgröße ausschließlich aus der Transformation einer Eingangsgröße, so ergibt sich ein direktes Verhältnis zwischen Ursache und Wirkung. Dies bedingt auch, dass die Ausgangsgröße vor einer Anregung keine sich ändernde Systemantwort liefert. Ein System, in welchem diese Bedingungen vorherrschen, wird als kauseles System bezeichnet (vgl. Abbildung 3). So zeigt beispielsweise eine Gleichspannungsanregung eines Systems eine zeitlich indifferente Gleichstromantwort. Ein System, welches sich anders verhält, wird als nicht kausales Systeme bezeichnet. Wenn für \(t < t_0\) der Wert des Eingangssignals Null ist, muss der Wert des Ausgangssignals für denselben Zeitraum ebenfalls Null sein, damit es die Bedingungen eins kausalen Systems erfüllt.

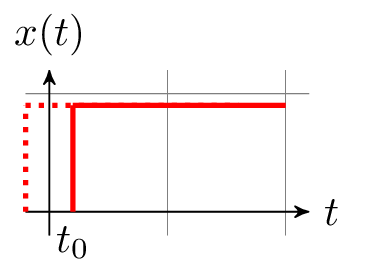
Die Abbildung zeigt links einen Zeitverlauf x(t), der bei t˙0 sprunghaft von 0 auf einen konstanten Wert ansteigt (Eingangssprung).
Dieses Signal x(t) wird in einen Block T eingespeist.
Rechts ist der Ausgangsverlauf y(t) dargestellt: Er beginnt ebenfalls bei t˙0, steigt jedoch nicht sprunghaft, sondern verzögert und kontinuierlich an, bis er sich auf einem neuen konstanten Niveau einpendelt.
Abbildung 3: Transformation eines kausalen Systems. Aus \(x(t)\) transformiertes System zu \(y(t)\) für ein kausales System.

Zeitinvarianz

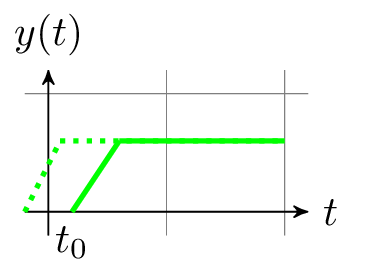
Reagiert das Ausgangssignal eines Systems zeitlich immer gleich auf ein Eingangssignal, so wird von einem zeitinvarianten Systemen gesprochen. Verschiebt sich der Zeitpunkt des Eingangssignals beispielsweise um \(t_0\), so muss weiterhin bei zeitinvarianten Systemen das Ausgangssignal immer gleich, ausgehend vom Eingangssignal, reagieren.

Die Stabilität eines Systems beschreibt ebenfalls einen Zusammenhang zwischen dem Eingangssignal und dem Ausgangssignal. Stellt sich bei einem Eingangssignal mit endlicher Amplitude ein nicht über alle Grenzen wachsendes Ausgangssignal ein, ist das System stabil. Wächst das Ausgangssignal nach der Inaktivierung des Eingangssignales weiter, ist das Systen instabil.

\begin {equation} T(\alpha \cdot u_\mathrm {e})=\alpha \cdot T(u_\mathrm {e}) \label {GleichungLinearität} \end {equation}

Linearität

Ist die Reaktion des Ausgangssignals zu der Anregung des Eingangssinals proportional, wird das System als lineares System beschrieben (Gleichung 3). Wirken zwei überlagerte Eingangssignale in ein System, so können sie in diesem Fall separat betrachtet und aufsummiert werden. Auf diese Weise können auch die Transformationen der Eingangssignale, wie in der Gleichung 4, getrennt betrachtet werden.

\begin {equation} T(u_1+u_2)=T(u_1)+T(u_2) \label {GleichungÜberlagerteSignale} \end {equation}

Systeme, die sowohl zeitinvariant, als auch linear sind, werden als LTI-Systeme (Linear Time Invariant) bezeichnet. Die Systeme in diesem betrachteten Modul werden in Näherung als LTI-Systeme betrachtet. Bauelemente, welche Nichtlinearitäten aufweisen, werden beispielsweise im Kapitel über periodische Größen behandelt.

Merke: LTI-Systeme

LTI-Systeme stellen lineare und zeitinvariante Systeme dar. Gleichstromnetzwerke müssen als LTI-Systeme betrachtet werden, damit der Überlagerungssatz auf sie angewendet werden kann.

2 Überlagerungssatz

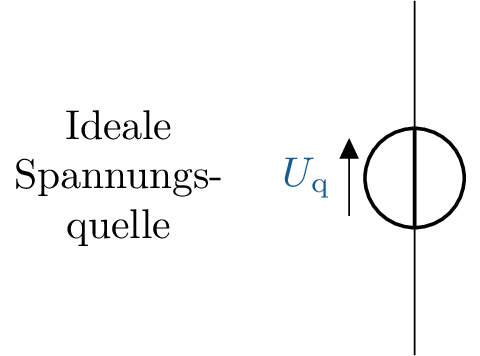
Sind die elektrischen Netzwerke als betrachtete Systeme auf ihre vorhandene Linearität geprüft, kann der Überlagerungssatz angewendet werden. Hier können verschiedene Quellen von einander getrennt betrachtet werden. Auf diese Weise werden beim Überlagerungssatz alle Quellen ausgeschaltet und reihenweise die einzelnen Quellen eingeschaltet. Beim Ausschalten von Quellen werden Stromquellen und Spannungsquellen verschieden umgewandelt. Beim Ausschalten einer idealen Spannungsquelle entsteht nach Abbildung 4 am Ort der Spannungsquelle ein Kurzschluss.

Die Grafik zeigt links eine ideale Spannungsquelle.
Ein Pfeil weist auf eine Ersatzschaltung rechts hin.
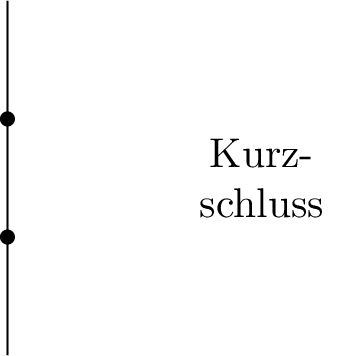
Die Ersatzschaltung rechts zeigt nur noch eine durchgehende vertikale Leitung mit zwei Klemmen. Damit wird veranschaulicht, dass eine ideale Spannungsquelle im ausgeschalteten bzw. genullten Zustand (U˙q=0) durch einen Kurzschluss ersetzt werden kann.
Abbildung 4: Umwandlung einer Spannungsquelle. Wird eine Spannungsquelle deaktiviert, verbleibt ein Kurzschluss. Mit diesem Kurzschluss erfolgt die weitere Netzwerkberechnung.

Eine Stromquelle hinterlässt beim Ausschalten lediglich offene Klemmen (Abbildung 5). Dieser Leerlauf verhindert die weitere Betrachtung dieses Pfades im Netzwerk.

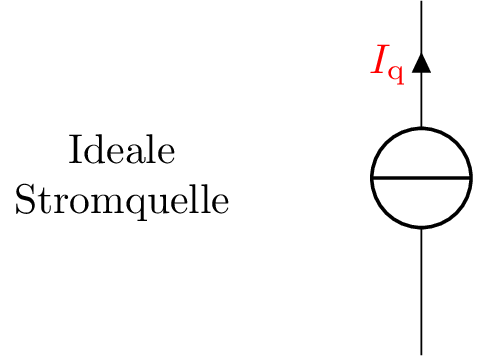
Die Abbildung zeigt links eine ideale Stromquelle.
Ein Pfeil weist auf die Ersatzschaltung rechts hin.
Die Ersatzschaltung rechts hin zeigt nur noch zwei voneinander getrennte Klemmen ohne Verbindung. Damit wird veranschaulicht, dass eine ideale Stromquelle im genullten Zustand (I˙q=0) durch einen Leerlauf, also offene Klemmen, ersetzt wird.
Abbildung 5: Umwandlung einer Stromquelle. Die Deaktivierung einer Stromquelle hinterlässt offene Klemmen.

Merke: Umwandlung von Quellen

Beim Ausschalten von Spannungsquellen und Stromquellen hinterlassen deaktivierte Spannungsquellen einen Kurzschluss und deaktivierte Stromquellen einen Leerlauf.

Sind bis auf eine Quelle alle anderen Quellen ausgeschaltet, wird das elektrische Netzwerk für die übriggebliebene Quelle analysiert. Das wird dann aufeinanderfolgend mit jeder Quelle durchgeführt. Am Ende werden die Einzelwirkungen als Summe betrachtet. Beispielsweise lässt sich der Strom \(I_\mathrm {R}\) durch einen Widerstand R, welcher von zwei Quellen \(Q_1\) und \(Q_2\) versorgt wird, durch die Summe der Teilströme der beiden Quellen erklären (vgl. Gleichung 5).

\begin {equation} I_\mathrm {R}=f(Q_1,Q_2) \label {GleichungZweiQuellen} \end {equation}

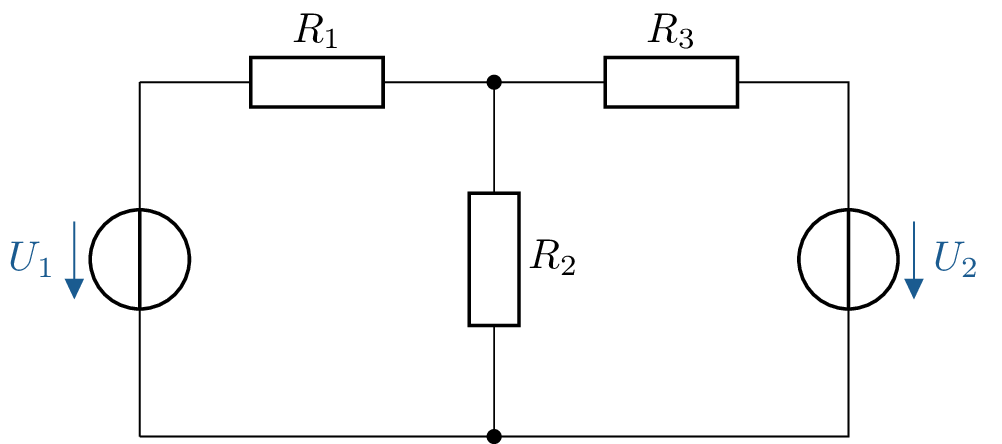
Zur Verdeutlichung des Überlagerungssatzes wird in der Abbildung 6 ein elektrisches Netzwerk mit zwei Spannungsquellen und drei Widerständen abgebildet. Um dieses Netzwerk mit mehr als einer Quelle zu berechnen, wird das Netzwerk für beide Spannungsquellen einzeln betrachtet.

Die Schaltung besteht aus einem rechteckigen Leitungsrahmen mit zwei Spannungsquellen U˙1 links und U˙2 rechts, deren Pfeile beide nach unten zeigen. Oben liegen zwei Widerstände in Serie: links R˙1 zwischen der linken Quelle und einem mittleren Knoten, rechts R˙3 zwischen diesem Knoten und der rechten Quelle. Vom mittleren oberen Knoten führt senkrecht nach unten ein weiterer Widerstand R˙2 zu einem unteren Knoten, der die beiden unteren Anschlüsse der Spannungsquellen verbindet.

Abbildung 6: Elektrisches Netzwerk mit zwei Spannungsquellen zur Erklärung des Überlagerungssatzes. Die Spannungsquellen sollen nacheinander für das elektrische Netzwerk analysiert werden.

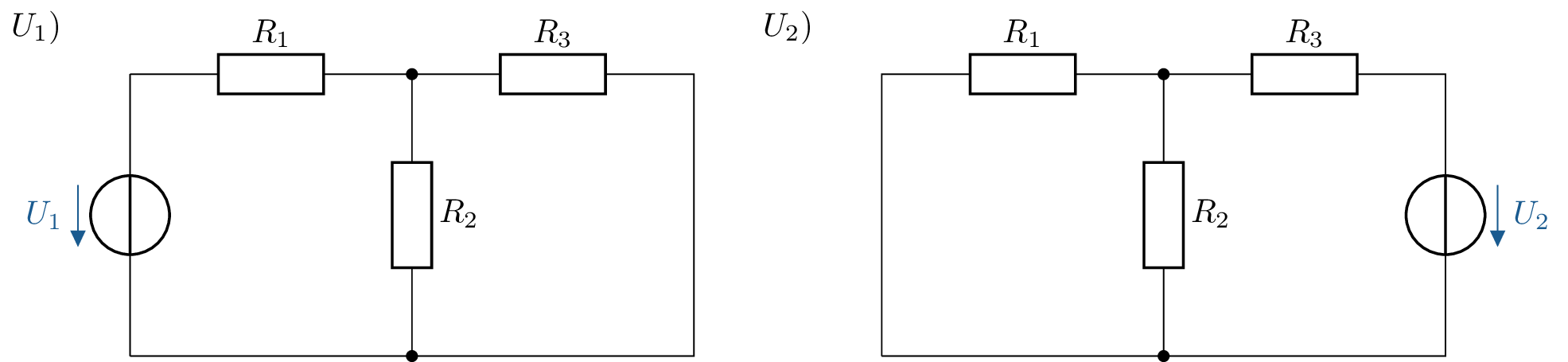
Das vorgestellte elektrische Netzwerk wird in der Abbildung 7 noch einmal jeweils für die Berechnung der beiden Spannungsquellen seperat angezeigt. Für die Netzwerkbetrachtung mit der Spannungsquelle \(U_1\) wird die Spannungsquelle \(U_2\) kurzgeschlossen. Die beiden Widerstände \(R_2\) und \(R_3\) liegen nun parallel zueinander. Die Spannung von \(U_1\) verteilt sich nun über \(R_1\) und die Parallelschaltung \(R_{23}\). Äquivalent dazu wird bei der Betrachtung des Netzwerkes für die Spannungsquelle \(U_2\) die Spannungsquelle \(U_1\) kurzgeschlossen. Nun bilden die beiden Widerstände \(R_1\) und \(R_2\) eine Parallelschaltung. Die Spannung der Spannungsquelle \(U_2\) verteilt sich über die Parallelschaltung \(R_{12}\) und den Widerstand \(R_3\).

Die Abbildung zeigt zwei getrennte Schaltungen mit identischer Widerstandsanordnung R˙1, R˙2, R˙3: Oben liegen R˙1 und R˙3 in Serie, vom Knoten zwischen ihnen führt der Widerstand R˙2 senkrecht nach unten zum unteren gemeinsamen Rückleiter. Links ist im Fall U˙1 nur die linke Spannungsquelle U˙1 in Serie mit dem Netzwerk aktiv, die rechte Quelle ist durch eine Leitung (Kurzschluss) ersetzt. Rechts ist im Fall U˙2 nur die rechte Spannungsquelle U˙2 aktiv, während die linke Quelle durch eine direkte Verbindung ersetzt ist.

Abbildung 7: Elektrisches Netzwerk mit zwei Spannungsquellen zur Erklärung des Überlagerungssatzes. Links wird das Netzwerk für die Analyse der Spannungsquelle \(U_1\) und rechts für die Spannungsquelle \(U_2\) gezeigt.

In der Gleichung 6 und der Gleichung 7 werden die Spannungen für die beiden Spannungsquellen \(U_1\) und \(U_2\) am Widerstand \(R_3\) separat bestimmt. In der Gleichung 8 werden die beiden Spannungen über den Widerstand \(R_3\) dann nach dem Überlagerungssatz aufsummiert.

\begin {equation} U_\mathrm {R3}(U_1) = U_1 \cdot \frac {R_\mathrm {23}}{R_1+R_\mathrm {23}} \label {GleichungU1} \end {equation} \begin {equation} U_\mathrm {R3}(U_2) = U_2 \cdot \frac {R_\mathrm {12}}{R_3+R_\mathrm {12}} \label {GleichungU2} \end {equation} \begin {equation} U_\mathrm {R3} = U_\mathrm {R3}(U_1) + U_\mathrm {R3}(U_2) \label {GleichungUR3} \end {equation}

Merke: Überlagerungssatz

Lineare und zeitlich invariante elektrische Netzwerke mit mehr als einer Quelle können als Summe der Teilanalysen von jeder einzelnen Quelle bestimmt werden.

Beispiel 1: Superpositionsverfahren

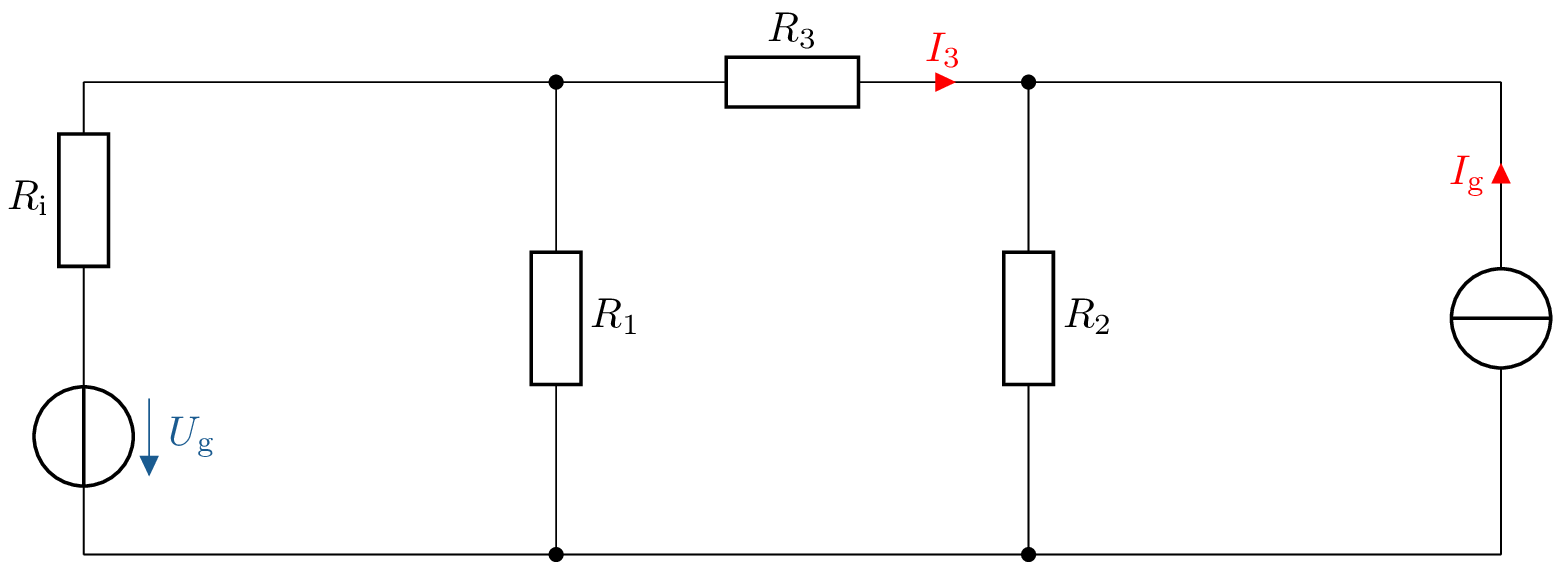
Gegeben ist das elektrische Netzwerk nach Abbildung 8. Die folgenden Aufgaben sollen bearbeitet werden:

Anwendung des Superpositionsverfahrens (Überlagerungssatz):
a)
Einzeichnen der Ströme und Spannungen
b)
Netzwerkberechnung \(I_3\) für \(U_\mathrm {g}\)
c)
Netzwerkberechnung \(I_3\) für \(I_\mathrm {g}\)
d)
Wie groß ist der Strom \(I_3\)
Die Schaltung besteht aus einem rechteckigen Rahmen mit drei senkrechten Zweigen zwischen einer gemeinsamen oberen und unteren Sammelschiene. Links liegt eine Spannungsquelle U˙g mit einem Serienwiderstand R˙i, in der Mitte ein Widerstand R˙1, rechts ein Widerstand R˙2 sowie ganz außen eine Stromquelle mit Strom I˙g nach oben. Oben verbindet der Widerstand R˙3 den Knoten über R˙1 mit dem Knoten über R˙2; durch R˙3 fließt der Strom I˙3 von links nach rechts.
Abbildung 8: Beispiel. Netzwerkanalyse mit Kirchhoffschen Regeln.
a)
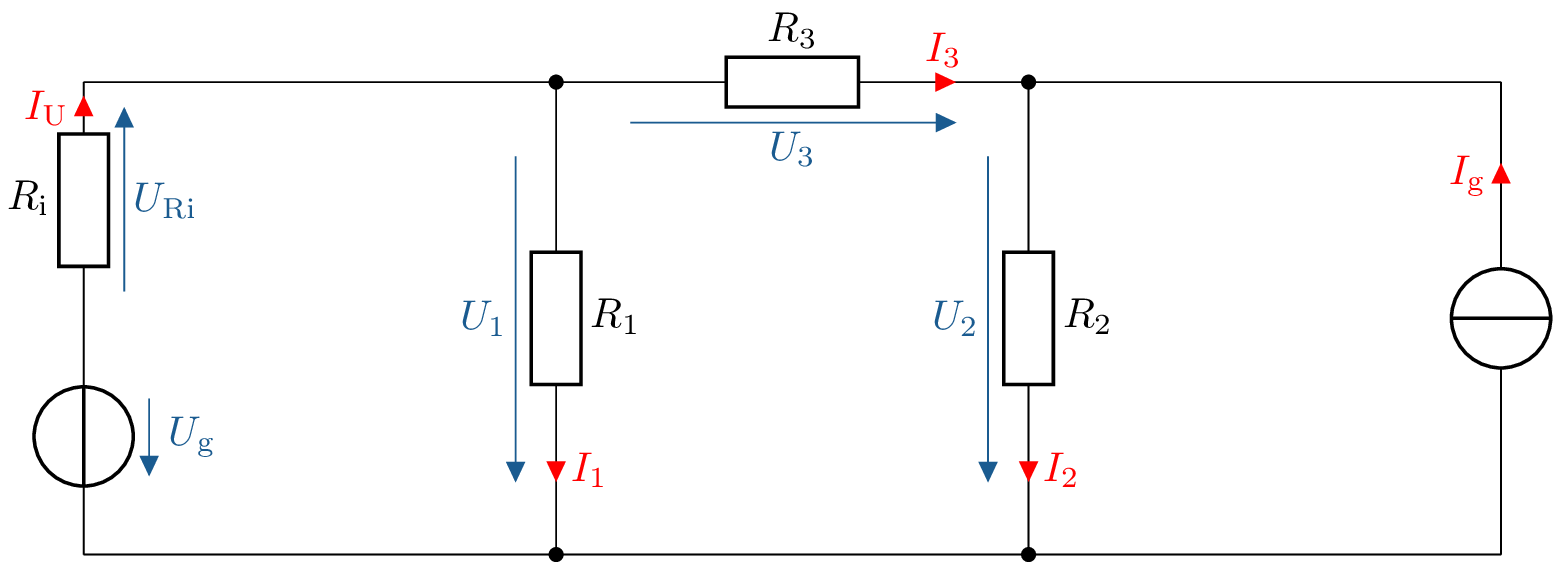
Angabe der Ströme und Spannungen:
Die Schaltung besteht aus zwei horizontalen Sammelschienen (oben und unten), zwischen denen drei senkrechte Widerstandszweige liegen: links die Serienschaltung aus Spannungsquelle U˙g und Innenwiderstand R˙i, in der Mitte R˙1, rechts R˙2. Über den drei Widerständen fallen die Spannungen U˙Ri, U˙1 und U˙2 nach unten ab, die zugehörigen Ströme I˙0, I˙1 und I˙2 sind ebenfalls nach unten eingezeichnet. Die oberen Knoten über R˙1 und R˙2 sind zusätzlich durch den Widerstand R˙3 mit Spannung U˙3 und Strom I˙3(von links nach rechts) verbunden, und ganz rechts speist eine Stromquelle mit Strom I˙g nach oben die obere Sammelschiene.
b)
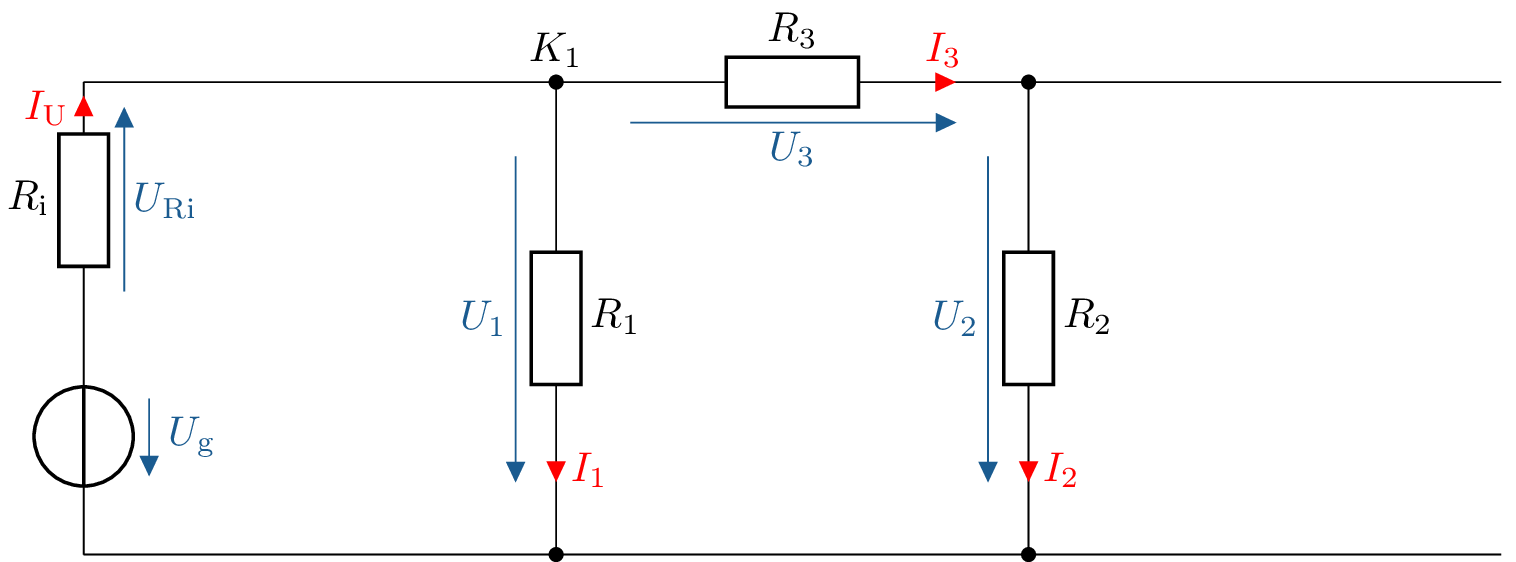
Netzwerkberechnung \(I_3(U_\mathrm {g})\) für \(U_\mathrm {g}\):
Die Schaltung hat zwei horizontale Sammelschienen (oben und unten), dazwischen drei senkrechte Zweige. Links liegt eine Spannungsquelle U˙g mit dem Serienwiderstand R˙i, durch den der Strom I˙0 nach oben fließt und die Spannung U˙Ri nach unten abgegriffen ist. In der Mitte und rechts stehen die Widerstände R˙1 und R˙2 mit Spannungen U˙1 und U˙2 sowie Strömen I˙1 und I˙2, jeweils nach unten gerichtet. Der obere Knoten über R˙1(Knoten K˙1) ist über den Widerstand R˙3 mit dem oberen Knoten über R˙2 verbunden; über R˙3 liegen die Spannung U˙3 und der Strom I˙3 von links nach rechts.

\begin {align} K_1: I_\mathrm {ges}&=I_1+I_3 \nonumber \\ I_\mathrm {ges}&=\frac {U_\mathrm {g}}{R_\mathrm {ges}}=\frac {U_\mathrm {g}}{R_\mathrm {i}+\frac {R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}} \nonumber \\ \frac {I_3}{I_\mathrm {ges}}&=\frac {R_1}{R_1+R_2+R_3} \nonumber \\ I_3(U_\mathrm {g})&=I_\mathrm {ges}\cdot \frac {R_1}{R_1+R_2+R_3}=\frac {U_\mathrm {g}}{R_\mathrm {i}+\frac {R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}}\cdot \frac {R_1}{R_1+R_2+R_3}\nonumber \end {align}

c)
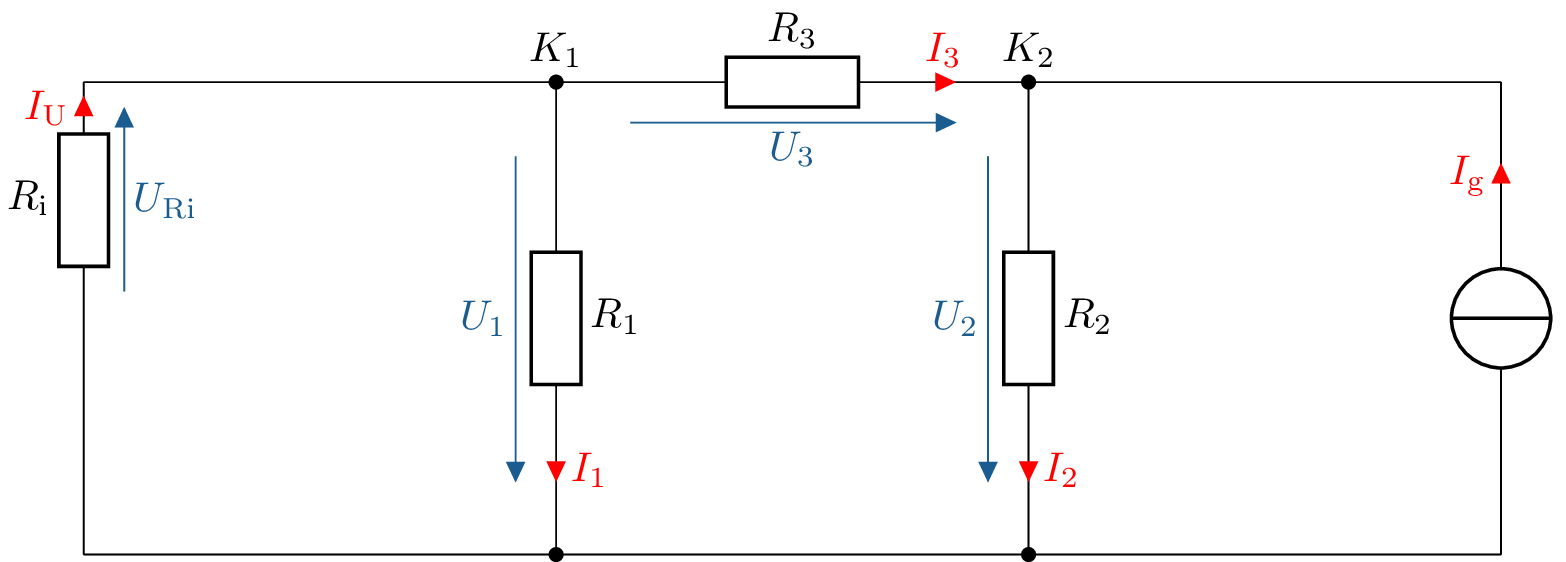
Netzwerkberechnung \(I_3(I_\mathrm {g})\) für \(I_\mathrm {g}\):
Die Schaltung hat zwei horizontale Sammelschienen (oben und unten), zwischen denen drei senkrechte Widerstände liegen: ganz links R˙i, in der Mitte R˙1, rechts R˙2; ganz rechts verbindet zusätzlich eine Stromquelle die untere mit der oberen Schiene. Die oberen Knoten über R˙1 und R˙2 heißen K˙1 bzw. K˙2 und sind über den Widerstand R˙3 verbunden, auf dem die Spannung U˙3 und der Strom I˙3 von links nach rechts eingezeichnet sind. Durch R˙i fließt der Strom I˙0 nach oben, durch R˙1 und R˙2 die Ströme I˙1 und I˙2 nach unten, und die Stromquelle rechts speist den Strom I˙g nach oben in die obere Schiene.

\begin {align} K_2: I_\mathrm {ges}&=I_\mathrm {g}=I_2-I_3 \nonumber \\ \frac {-I_3}{I_\mathrm {ges}}&=\frac {R_2}{(R_1||R_\mathrm {i})+R_2+R_3} \nonumber \\ I_3(I_\mathrm {g})&=-I_\mathrm {g}\cdot \frac {R_2}{(R_1||R_\mathrm {i})+R_2+R_3}\nonumber \end {align}

d)
Wie groß ist der Strom \(I_3(U_\mathrm {g},I_\mathrm {g})\)?

Superposition:
\begin {align} I_3(U_\mathrm {g},I_\mathrm {g}) &= I_3(U_\mathrm {g})+I_3(I_\mathrm {g}) \nonumber \\ I_3(U_\mathrm {g},I_\mathrm {g}) &= \frac {U_\mathrm {g}}{R_\mathrm {i}+\frac {R_1\cdot (R_2+R_3)}{R_1+R_2+R_3}}\cdot \frac {R_1}{R_1+R_2+R_3}+(-I_\mathrm {g}\cdot \frac {R_2}{(R_1||R_\mathrm {i})+R_2+R_3}) \nonumber \end {align}

Expand
×

...