Sprache wählen Icon

Knotenpotentialverfahren

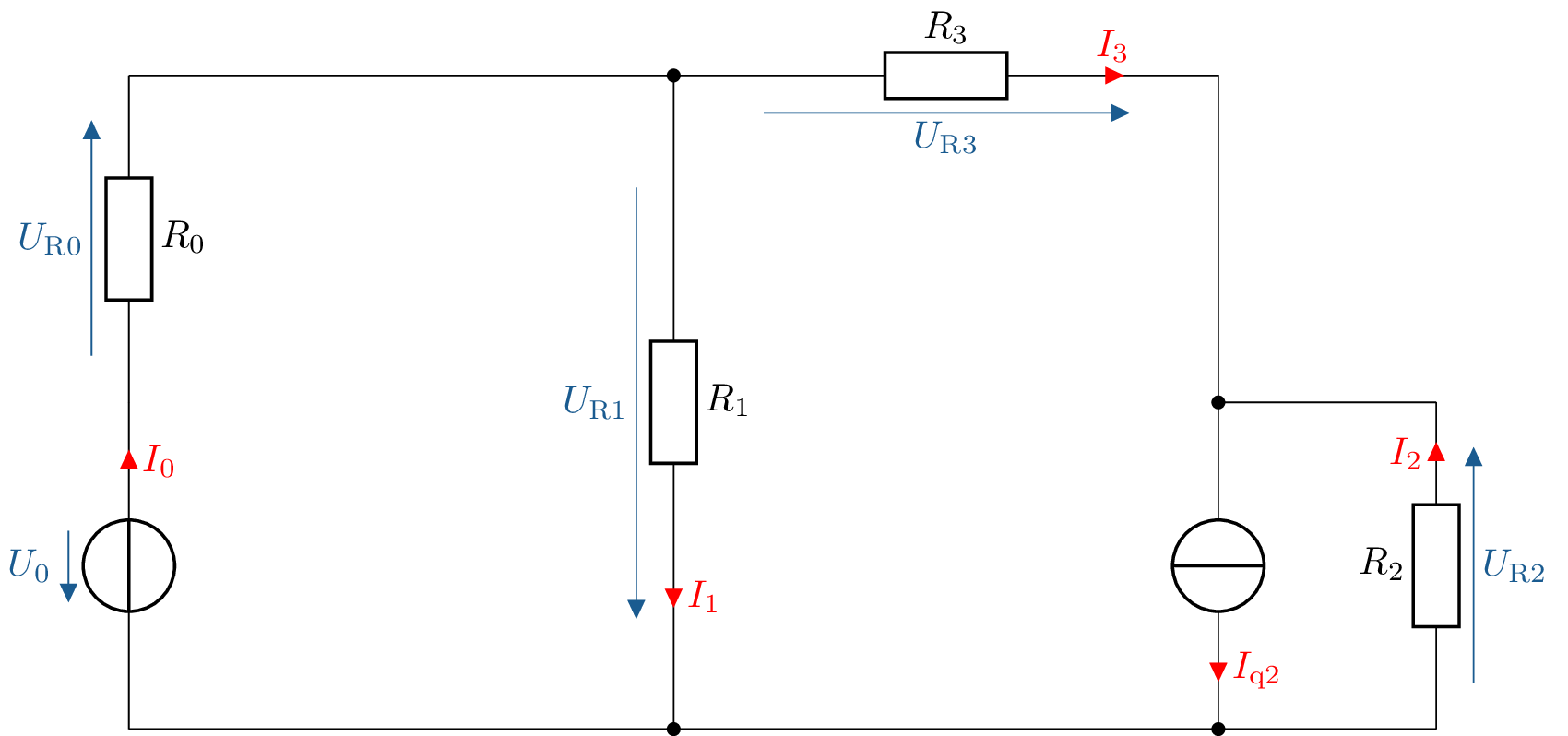
Die Analyse eines elektrischen Netzwerkes kann mitunter aufwendig werden. Mit größer werdendem Netzwerk steigt auch der Aufwand zur Analyse. Auch reichen unter Umständen die bisher vorgestellten Analysemethoden zu Knoten- und Maschenanalyse nicht aus, um alle Größen eines elektrischen Netzwerkes zu bestimmen. Hier bietet das Knotenpotentialverfahren eine Möglichkeit zur Analyse. Beim Knotenpotentialverfahren werden ausgehend von einem Bezugspotential, mit der Zuordnung 0V, alle übrigen Potentiale bestimmt. Mithilfe des Knotenpotentialverfahrens wird folgend das elektrische Netzwerk aus der Abbildung 1 analysiert.

Die Schaltung besitzt eine obere und eine untere Sammelschiene. Links speist eine Spannungsquelle U˙0 mit dem Serienwiderstand R˙0 den Rahmen, der Strom I˙0 fließt dabei nach oben, über R˙0 liegt die Spannung U˙R0. In der Mitte verbindet der Widerstand R˙1(mit U˙R1, Strom I˙1 nach unten) die beiden Schienen, rechts oben liegt der Widerstand R˙3 zwischen dem mittleren oberen Knoten und einem rechten oberen Knoten, mit Spannung U˙R3 und Strom I˙3 nach rechts. Von diesem rechten oberen Knoten führen zwei parallele Zweige zur unteren Schiene: ein Widerstand R˙2 mit Spannung U˙R2 und Strom I˙2 nach oben sowie eine Stromquelle mit Quellenstrom I˙q2 nach unten.

Abbildung 1: Netzwerk für das Knotenpotentialverfahren. Elektrisches Netzwerk mit einer Spannungsquelle, einer Stromquelle und vier Widerständen. Anhand des Netzwerkes wird das Knotenpotentialverfahren erläutert.

Lernziele: Knotenpotentialverfahren

Die Studierenden

  • kennen die Schritte des Knotenpotentialverfahrens.
  • können mit Hilfe des Knotenpotentialverfahrens elektrische Netzwerke analysieren.

1 Vorbereitung des Netzwerkes

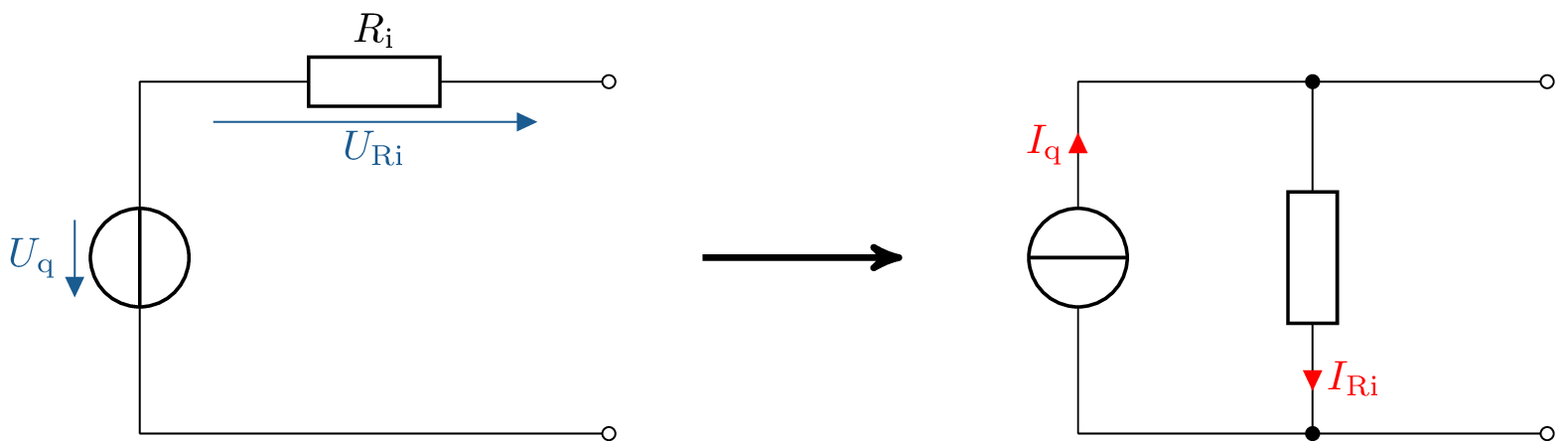
Das Knotenpotentialverfahren arbeitet mit Stromquellen und Leitwerten. Das vorgestellte Netzwerk weist neben der Stromquelle eine Spannungsquelle und Widerstandswerte auf. Diese gilt es umzuwandeln. Die Spannungsquelle wird wie in der Abbildung 2 zu einer Stromquelle transformiert. Dabei wird aus dem Reihenwiderstand der Spannungsquelle ein Parallelwiderstand für die Stromquelle.

Die Abbildung zeigt links eine ideale Spannungsquelle U˙q mit einem Serienwiderstand R˙i; die Quellspannung fällt über R˙i als U˙Ri ab. Ein Pfeil weist auf eine rechts dargestellte Ersatzschaltung, in der eine ideale Stromquelle mit Strom I˙q parallel zu demselben Widerstand R˙i liegt; durch R˙i fließt der Strom I˙Ri nach unten. Es wird damit die Umwandlung der Spannungsquelle mit Innenwiderstand in die äquivalente Stromquellenschaltung illustriert.

Abbildung 2: Umwandlung einer Spannungsquelle. Umwandlung einer Spannungsquelle mit Reihenwiderstand zur Stromquelle mit Parallelwiderstand.

Bei der Umwandlung der Spannungsquellen in Stromquellen müssen auch die Spannungswerte der Spannungsquellen in Stromwerte überführt werden. Dies erfolgt nach Gleichung 1.

\begin {equation} I_\mathrm {q} = U_\mathrm {q} \cdot G_\mathrm {i} \label {GleichungUmrechnungSpannungsquelle} \end {equation}

Da bei dem Knotenpotentialverfahren nicht die Widerstandswerte der Komponenten verwendet werden, sondern die Leitwerte, werden alle Widerstandswerte nach Gleichung 2 in Leitwerte umgerechnet.

\begin {equation} G_\mathrm {i} = \frac {1}{R_\mathrm {i}} \label {GleichungUmrechnungWiderstand} \end {equation}

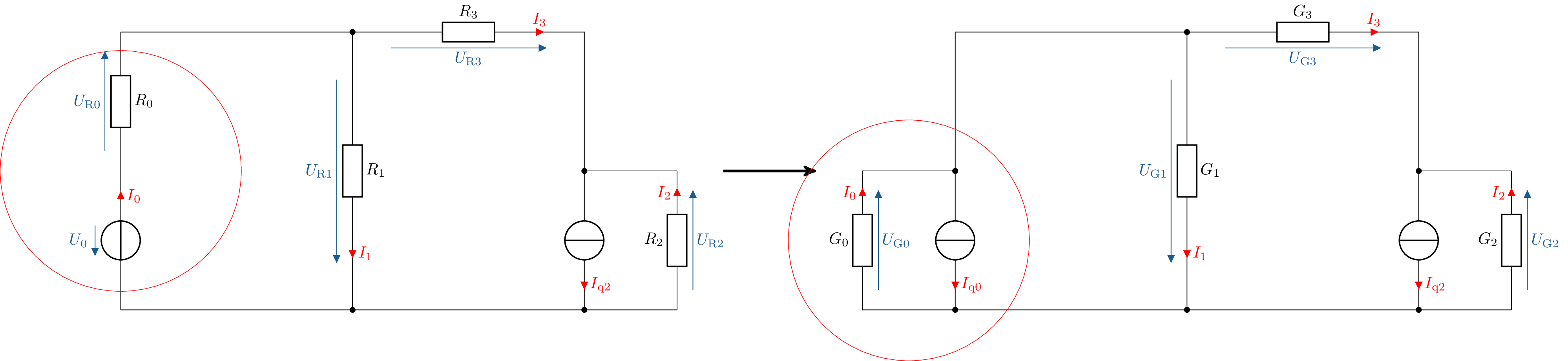
In der Abbildung 3 wird die Umwandlung der Spannungsquellen aus dem angegeben Netzwerk in eine äquivalente Stromquellen dargestellt. Aus der Spannungsquelle \(U_0\) und dem Widerstand \(R_0\) wird die Stromquelle \(I_\mathrm {q0}\) und dazu der parallel liegende Leitwert \(G_0\). Die restlichen Widerstände werden ebenfalls in Leitwerte überführt.

Die Abbildung zeigt zwei nahezu identische Schaltungen, links und rechts nebeneinander, verbunden durch einen Pfeil. In der linken Schaltung ist der linke Zweig rot eingekreist: eine Spannungsquelle U˙q0 mit einem Serienwiderstand R˙i0. In der rechten Schaltung ist derselbe Zweig wieder rot eingekreist, jetzt jedoch als äquivalente Stromquelle I˙q0 mit einem parallel dazu liegenden Leitwert bzw. Widerstand G˙i0 dargestellt. Alle übrigen Zweige der Schaltung bleiben unverändert.

Abbildung 3: Umwandlung des Netzwerkes für das Knotenpotentialverfahren. Die Spannungsquelle \(U_0\) wird zu der Stromquelle \(I_\mathrm {q0}\), außerdem werden die Widerstandsangaben R zu Leitwerten G.

Merke: Knotenpotentialverfahren

Beim Knotenpotentialverfahren wird ein elektrisches Netzwerk mit Stromquellen und Leitwerten analysiert.

2 Bestimmung der Knoten und der Knotenpotentiale

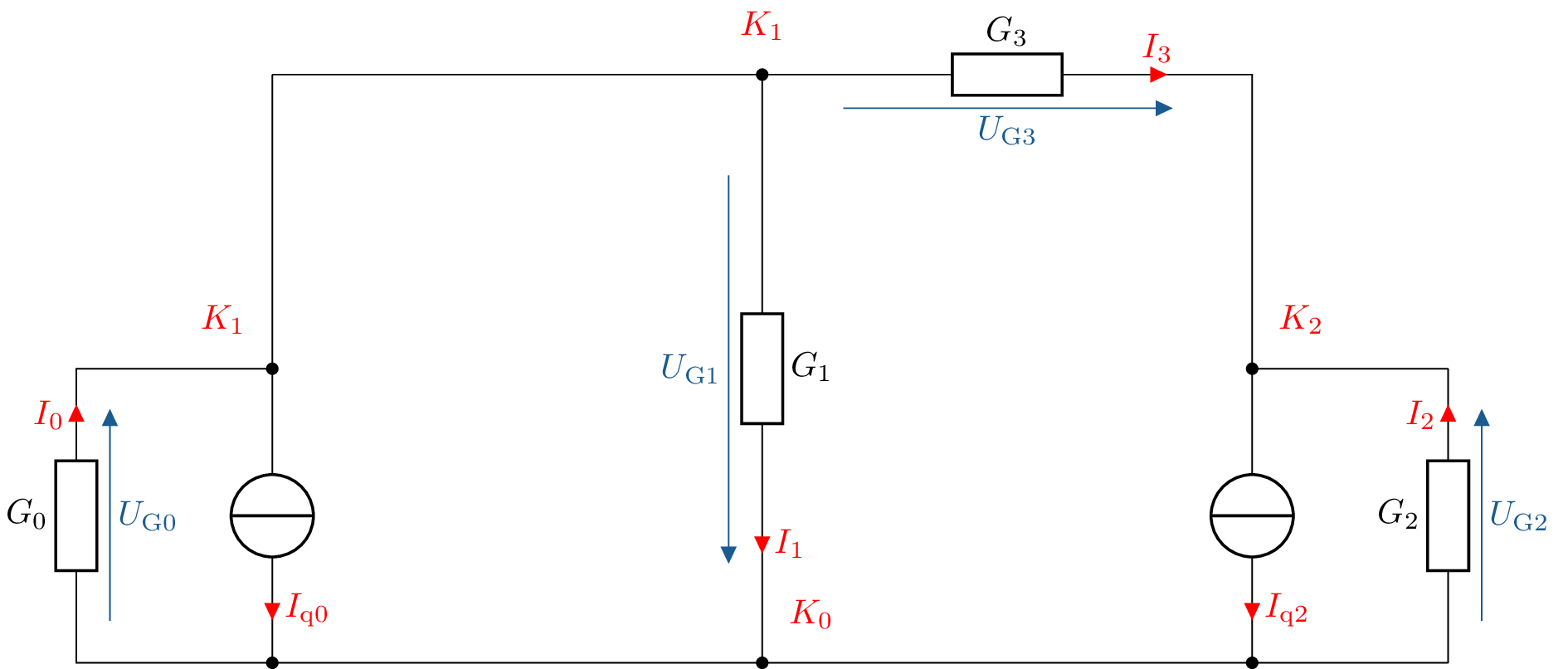
Nun müssen die Knoten bestimmt werden. Hierzu legen wir einen Bezugsknoten mit dem Index 0, also \(K_0\), fest. Weiter werden alle Knoten fortlaufend nummeriert. Das elektrische Netzwerk mit den nummerierten Knoten wird in der Abbildung 4 abgebildet. Die eingezeichneten Knoten ohne Komponenten zwischen den nummerierten Knoten weisen das identische Potential auf und bilden somit einen Knoten.

Die Schaltung besitzt eine obere und eine untere Sammelschiene; dazwischen liegen drei senkrechte Leitwerte G˙0(links), G˙1(Mitte) und G˙2(rechts). Über G˙0 und G˙2 fließen die Ströme I˙0 bzw. I˙2 von unten nach oben bei den Spannungen U˙G0 und U˙G2, parallel dazu sind jeweils Stromquellen I˙q0 und I˙q2 von oben nach unten zwischen denselben Knoten geschaltet. Die oberen Knoten K˙1 und K˙2 sind über den waagerechten Leitwert G˙3 mit Strom I˙3 nach rechts und Spannung U˙G3 verbunden, während G˙1 den oberen Leiter mit dem unteren Knoten K˙0 verbindet (Strom I˙1 nach unten, Spannung U˙G1).

Abbildung 4: Umgewandeltes Netzwerk. Festlegung des Bezugsknotens \(K_0\) und der fortlaufenden Knoten \(K_1\) und \(K_2\).

Um die Knotenpotentiale festzulegen, werden alle Potentiale der Knoten \(K_1\) und \(K_2\) auf den Bezugsknoten bezogen. Zur Durchführung des Knotenpotentialverfahrens werden \(k-1\) Gleichungen benötigt. Auf das angegebene Netzwerk bezogen, ergeben sich somit zwei Gleichungen, welche in vektorieller Schreibweise nach Gleichung 3 notiert werden. Hier wird das Potential für den Knoten \(K_1\) über die Spannung vom Knoten \(K_1\) zum Bezugknoten definiert. Daraus ergibt sich die Notation \(U_\mathrm {K1-K0}\). Selbiges wird für den Knoten \(K_2\) durchgeführt. Hier wird die Spannung \(U_\mathrm {K2-K0}\) definiert.

\begin {equation} U_\mathrm {K} = \begin {bmatrix} U_\mathrm {K1-K0} \\ \\ U_\mathrm {K2-K0} \\ \end {bmatrix} \label {GleichungKnotenpotentiale} \end {equation}

3 Zuordnung der Quellströme

Für die festgelegten Knoten, abgesehen vom Bezugsknoten, müssen die abfließenden und zufließende Ströme festgehalten werden. Jede Stromquelle an den Knoten wird notiert. Hier werden zufließende Stromquellen mit einem positiven Vorzeichen und abfließende Stromquellen mit einem negativen Vorzeichen versehen. Aus dem Knoten \(K_1\) fließt der Strom der Stromquelle \(-I_\mathrm {q0}\), dieser Strom wird mit einem negativen Vorzeichen versehen. Aus dem Knoten \(K_2\) fließt der Strom der Stromquelle \(-I_\mathrm {q2}\) heraus, dieser wird ebenfalls mit einem negativen Vorzeichen versehen. Nach Gleichung 4 ergibt sich der Vektor für die Quellströme.

\begin {equation} I_\mathrm {K} = \begin {bmatrix} -I_\mathrm {q0} \\ \\ -I_\mathrm {q2} \\ \end {bmatrix} \label {GleichungQuellströme} \end {equation}

4 Leitwertmatrix

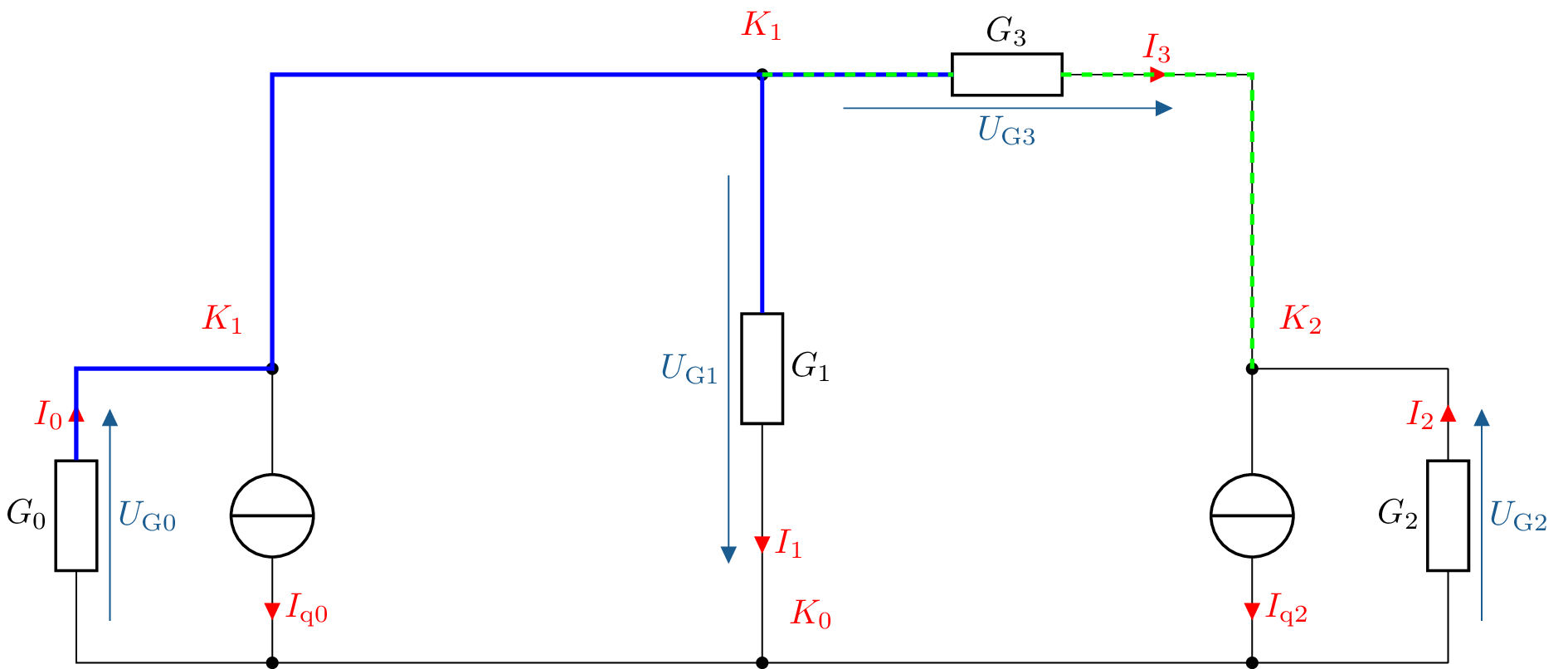
Nach der Umwandlung der Widerstandswerte in Leitwerte, wird mit den Leitwerten die Leitwertmatrix erstellt. Hierzu werden wieder die Knoten abgesehen vom Bezugsknoten untersucht. Hierfür wird das vorgestellte elektrische Netzwerk noch einmal in der Abbildung 5 mit farbig hervorgehobenen Zweigen gezeigt. Über die Hauptdiagonale werden die Leitwerte der Knoten notiert. Für jeden Knoten werden die Leitwerte der direkt angrenzenden Komponenten aufgeschrieben. Für den Knoten \(K_1\) wären das die an dem blau hervorgehobenen Zweig angrenzenden Leitwerte \(G_0\), \(G_1\) und \(G_3\) und für den Knoten \(K_2\) die Leitwerte \(G_2\) und \(G_3\). Abseits der Hauptdiagonalen auf den anderen Elementen der Leitwertmatrix werden die Leitwerte protokolliert, welche direkt zwischen den Knoten liegen. Zwischen den Knoten \(K_1\) und \(K_2\) liegt auf direktem Wege der in grün hervorgehobenen Zweig mit dem Leitwert \(G_3\). Liegen zwischen den betrachteten Knoten weitere Knoten, so sind diese nicht direkt miteinander Verbunden und in das Element der Leitwertmatrix wird eine 0 eingetragen. Die auf diese Weise angefertigte Leitwertmatrix wird in der Gleichung 5 veranschaulicht.

PIC

Abbildung 5: Elektrisches Netzwerk mit hervorgehobenen Zweigen. Erstellung der Leitwertmatrix für das Knotenpotentialverfahren

\begin {equation} G_\mathrm {K} = \begin {bmatrix} \color {blue}{G_0 + G_1 + G_3} & \color {green}{-G_3} \\ \\ \color {green}{-G_3} & G_2 + G_3 \\ \end {bmatrix} \label {GleichungLeitwertmatrix} \end {equation}

5 Gleichungssystem aufstellen

Nachdem der Vektor der Knotenpotentiale, der Vektor der Quellströme und die Leitwertmatrix bestimmt wurden, wird aus diesen Gleichungen das Gleichungssystem des Knotenpotentialverfahrens aufgestellt, welches in der Gleichung 5 angezeigt wird.

\begin {equation} \begin {bmatrix} G_0 + G_1 + G_3 & -G_3 \\ \\ -G_3 & G_2 + G_3 \\ \end {bmatrix} \cdot \begin {bmatrix} U_\mathrm {K1-K0} \\ \\ U_\mathrm {K2-K0} \\ \end {bmatrix} = \begin {bmatrix} -I_\mathrm {q0} \\ \\ -I_\mathrm {q2} \\ \end {bmatrix} \end {equation}

Das Gleichungssystem des Knotenpotentialverfahrens kann anschließend exemplarisch mit dem Gaußschen Eliminationsverfahren gelöst werden. Durch das Umstellen der Gleichung nach den gesuchten Knotenpotentialen können diese identifiziert werden. Ist so beispielsweise in dem untersuchten Netzwerk die Spannung über den Widerstand \(R_1\) berechnet worden, kann der Strom durch den Widerstand bestimmt werden. Als Alternative zum Gaußschen Eliminationsverfahren wäre noch die Cramersche Regel zu nennen um lineare Gleichungssysteme zu lösen.

Beispiel 1: Knotenpotentialverfahren

Analyse des elektrischen Netzwerk aus der Abbildung 6 mittels des Knotenpotentialverfahrens.

Die folgenden Schritte sollen für das Knotenpotentialverfahren bearbeitet werden:
  • Vorbereitung des Netzwerkes
  • Bestimmung der Knoten und der Knotenpotentiale
  • Zuordnung der Quellströme
  • Aufstellung der Leitwertmatrix
  • Gleichungssystem aufstellen
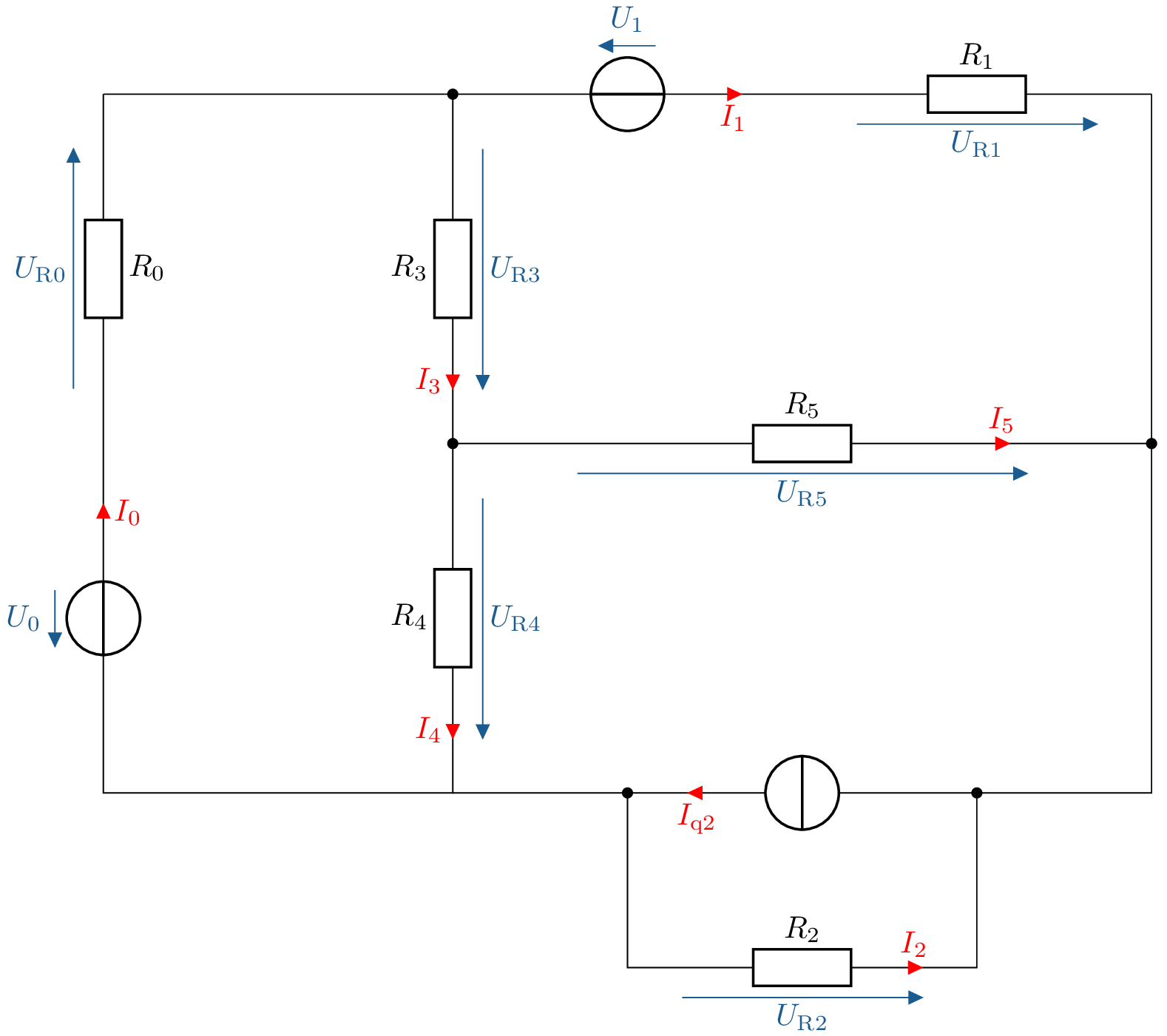
Die Abbildung zeigt einen rechteckigen Stromkreis mit oberer und unterer Sammelschiene. Links befindet sich eine Spannungsquelle U˙0 mit dem Serienwiderstand R˙0; in der Mitte verbindet eine vertikale Reihenschaltung aus R˙3 und R˙4 die beiden Schienen, rechts oben liegt ein Zweig aus Spannungsquelle U˙1 und Widerstand R˙1. Vom Knoten zwischen R˙3 und R˙4 führt ein horizontaler Zweig mit dem Widerstand R˙5 zum rechten Rahmen, und rechts unten ist eine Stromquelle parallel zu einem Widerstand R˙2 angeordnet. An allen Widerständen und Quellen sind die zugehörigen Spannungen U˙R0, U˙R3, U˙R4, U˙R5, U˙R2, U˙1, U˙0 sowie die Ströme I˙0, I˙1, I˙3, I˙4, I˙5, I˙q2, I˙2 eingezeichnet.
Abbildung 6: Beispiel. Knotenpotentialverfahren an einem elektrischen Netzwerk.
a)
Vorbereitung des Netzwerkes:
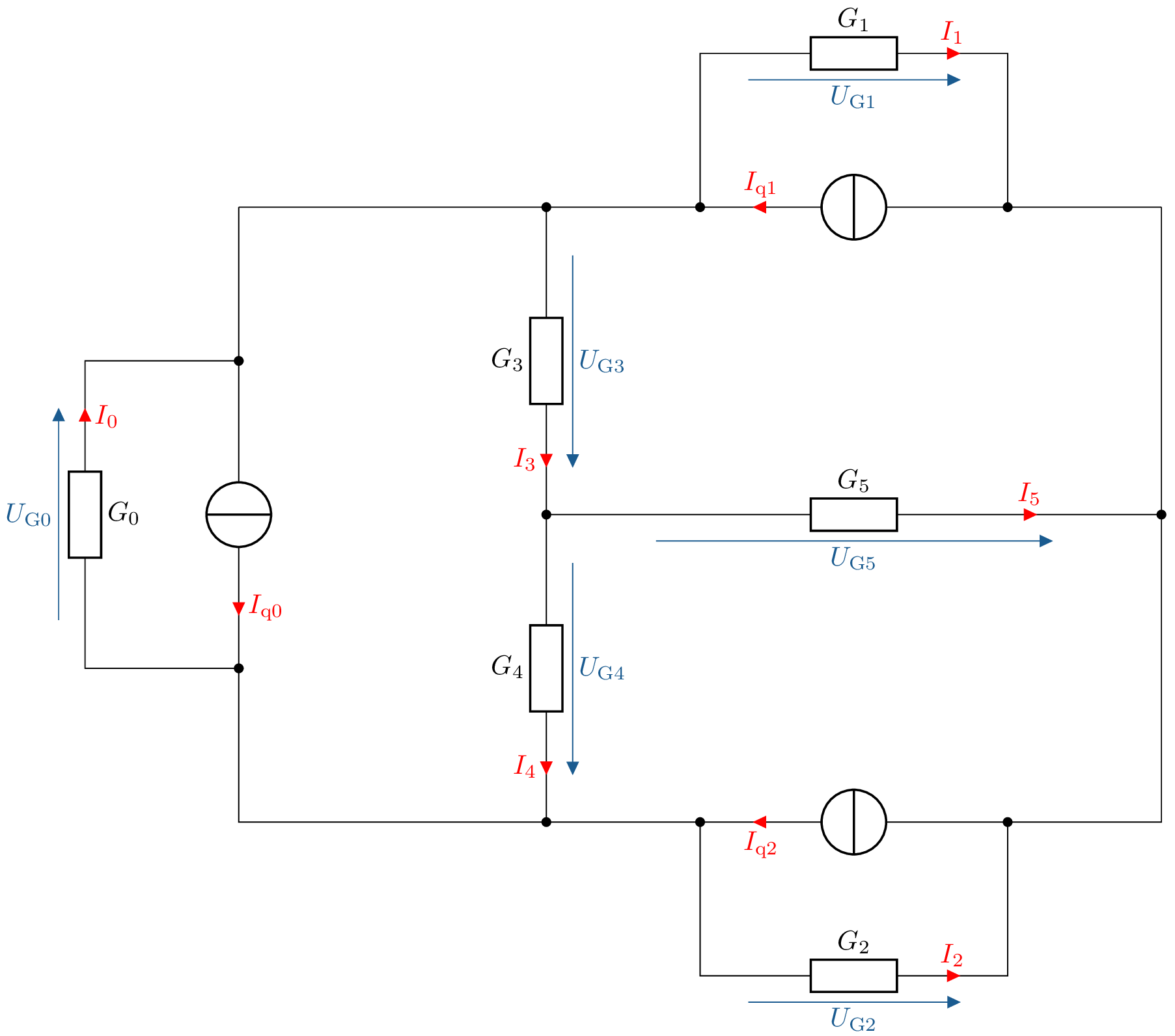
Die Schaltung besteht aus einer oberen und unteren Sammelschiene mit drei Hauptzweigen: links ein Leitwert G˙0 parallel zu einer Stromquelle I˙q0, in der Mitte die in Serie liegenden Leitwerte G˙3 und G˙4. Rechts ist der gemeinsame Knoten dieses Netzes über einen oberen Parallelzweig aus Leitwert G˙1 und Stromquelle I˙q1 sowie über einen unteren Parallelzweig aus Leitwert G˙2 und Stromquelle I˙q2 mit der unteren Schiene verbunden. Zwischen dem mittleren senkrechten Zweig und dem rechten Knoten liegt zusätzlich der horizontale Leitwert G˙5; an allen Leitwerten sind Spannungen U˙Gi und Ströme I˙i mit eingezeichneter Richtung markiert.
b)
Bestimmung der Knoten und der Knotenpotentiale:
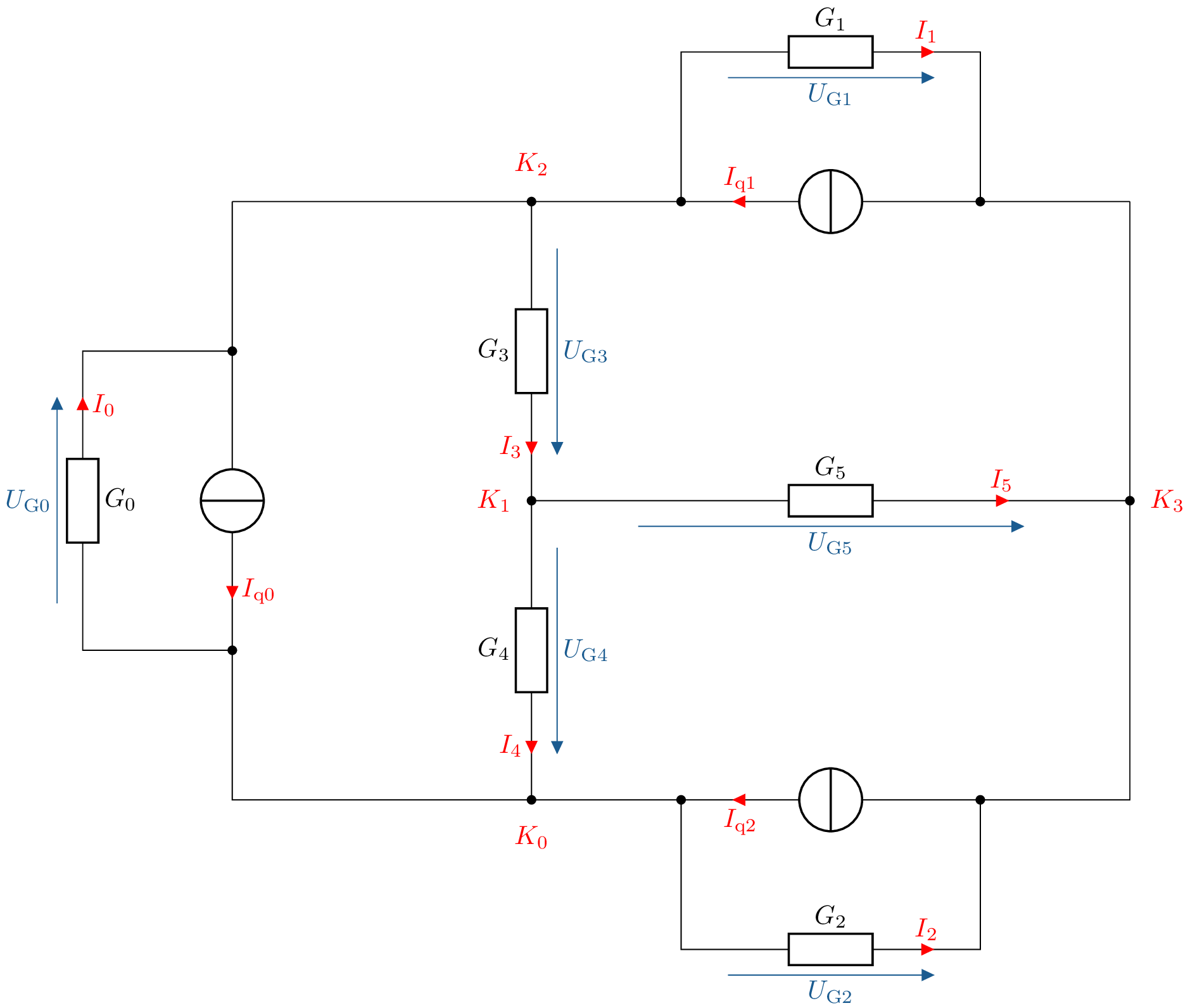
Die Schaltung besitzt vier Knoten K˙0, K˙1, K˙2 und K˙3, die durch einen rechteckigen Leitungsrahmen verbunden sind. Links liegt an K˙0 ein Zweig aus Leitwert G˙0(Strom I˙0 nach oben, Spannung U˙G0) parallel zu einer Stromquelle I˙q0. Zwischen K˙2 und K˙0 verläuft in der Mitte ein senkrechter Zweig mit den Leitwerten G˙3(oben) und G˙4(unten), vom Zwischenknoten K˙1 führt waagrecht der Leitwert G˙5 nach rechts zum Knoten K˙3. An K˙2 und K˙0 sind jeweils weitere Zweige angeschlossen: oben G˙1 parallel zu I˙q1, unten G˙2 parallel zu I˙q2, deren Ströme und Spannungen im Bild eingetragen sind.

\begin {equation} U_\mathrm {K} = \begin {bmatrix} U_\mathrm {K1-K0} \\ \\ U_\mathrm {K2-K0} \\ \\ U_\mathrm {K3-K0} \\ \end {bmatrix} \nonumber \end {equation}

c)
Zuordnung der Quellströme: \begin {equation} I_\mathrm {K} = \begin {bmatrix} 0 \\ \\ -I_\mathrm {q0}+I_\mathrm {q1} \\ \\ -I_\mathrm {q1}-I_\mathrm {q2} \\ \end {bmatrix} \nonumber \end {equation}
d)
Bestimmung der Leitwertmatrix: \begin {equation} G_\mathrm {K} = \begin {bmatrix} G_3 + G_4 + G_5 & -G_3 & -G_5 \\ \\ -G_3 & G_0 + G_1 + G_3 & -G_1 \\ \\ -G_5 & -G_1 & G_1 + G_2 + G_5 \\ \end {bmatrix} \nonumber \end {equation}
e)
Gleichungssystem aufstellen: \begin {equation} \begin {bmatrix} G_3 + G_4 + G_5 & -G_3 & -G_5 \\ \\ -G_3 & G_0 + G_1 + G_3 & -G_1 \\ \\ -G_5 & -G_1 & G_1 + G_2 + G_5 \\ \end {bmatrix} \cdot \begin {bmatrix} U_\mathrm {K1-K0} \\ \\ U_\mathrm {K2-K0} \\ \\ U_\mathrm {K3-K0} \\ \end {bmatrix} = \begin {bmatrix} 0 \\ \\ -I_\mathrm {q0}+I_\mathrm {q1} \\ \\ -I_\mathrm {q1}-I_\mathrm {q2} \\ \end {bmatrix}\nonumber \end {equation}
Expand
×

...