1 Knoten- und Maschenanalyse 1

Gegeben sind unten stehende Netzwerke.

• Stellen Sie die Maschengleichung für die Masche \(M_1\) auf!
• Stellen Sie die Knotengleichung für den Knoten \(K_0\) auf!

• Maschengleichungen: \begin {align} M_1 : U_1-U_\mathrm {Ri}-U_\mathrm {R1}-U_\mathrm {R2}-U_\mathrm {R3} &=0 \nonumber \end {align}
• Knotengleichungen: \begin {align} K_0 : +I_1+I_2-I_3+I_4-I_5 &=0 \nonumber \end {align}

2 Knoten- und Maschenanalyse 2

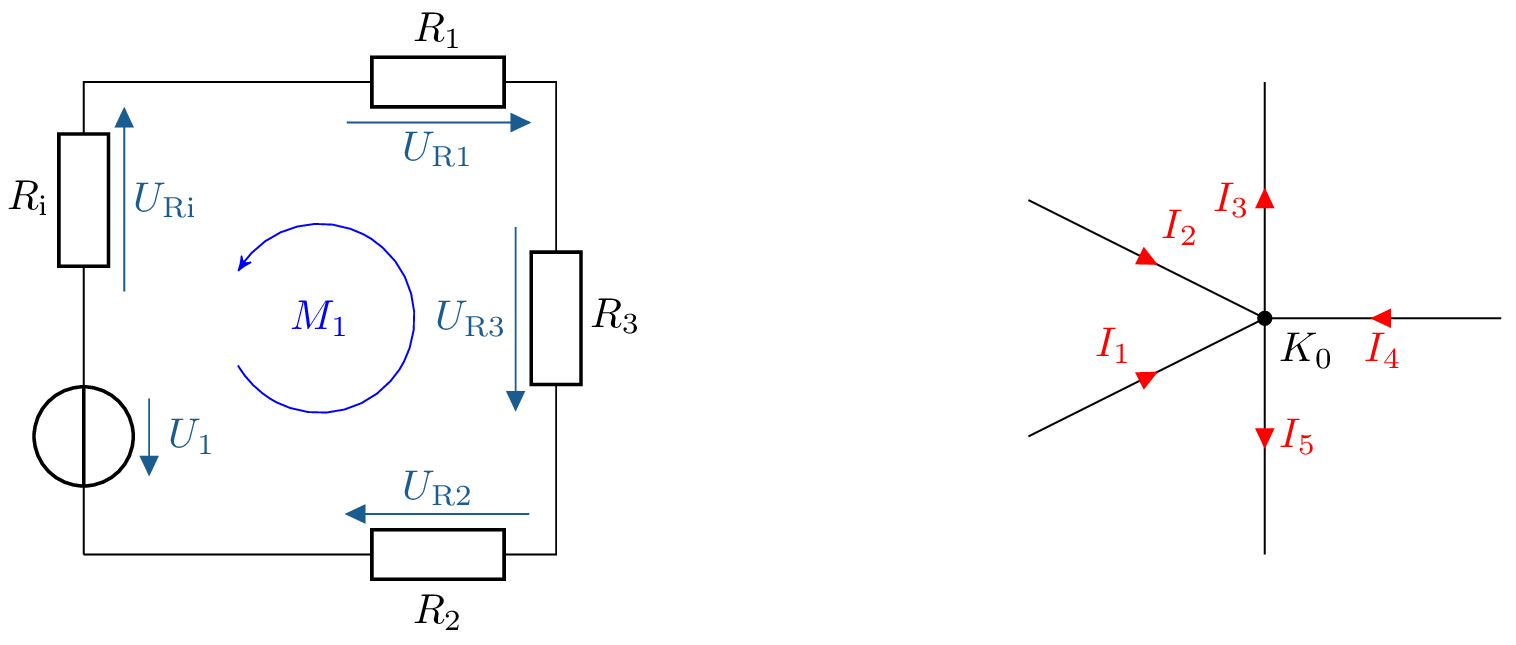
Gegeben ist unten stehendes Netzwerk.

• Wie viele Knoten, Zweige und Maschen werden zur Analyse benötigt?
• Zeichnen Sie einen vollständigen Baum zu dem angegebenen Netzwerk.

• Das Netzwerk verfügt über:
  

  • Knoten: k=6
  • Zweige: k-1=5
  • Maschen: 4

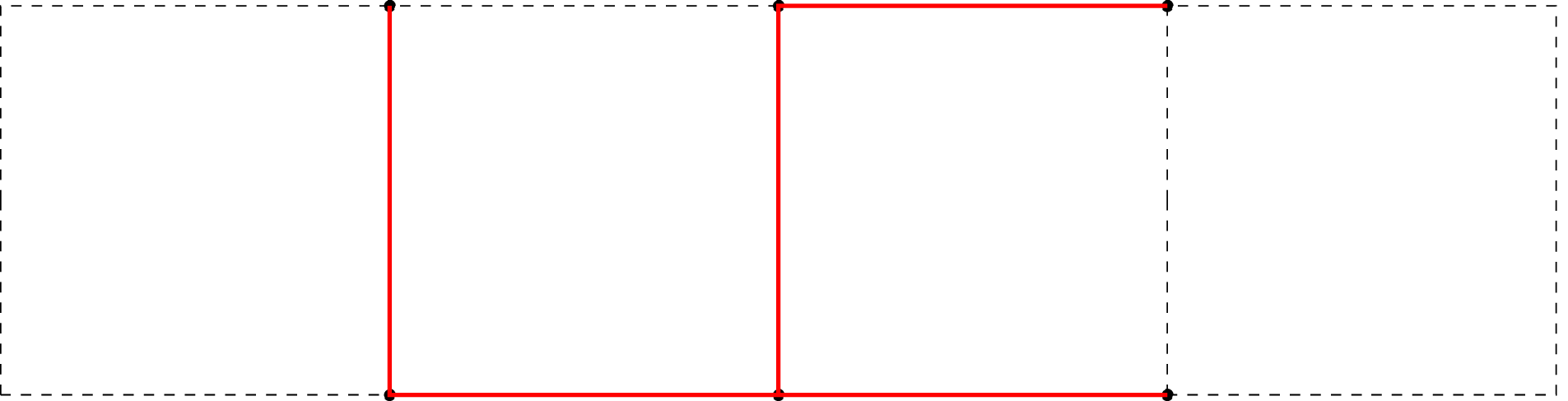
• Vollständiger Baum:
  

  

3 Knoten- und Maschenanalyse 3

Gegeben ist unten stehendes Netzwerk.

• Markieren und bennen Sie alle Ströme und Spannungen!
• Stellen Sie die Gleichungen für alle Knoten auf!
• Stellen Sie die Gleichungen für alle Maschen auf!

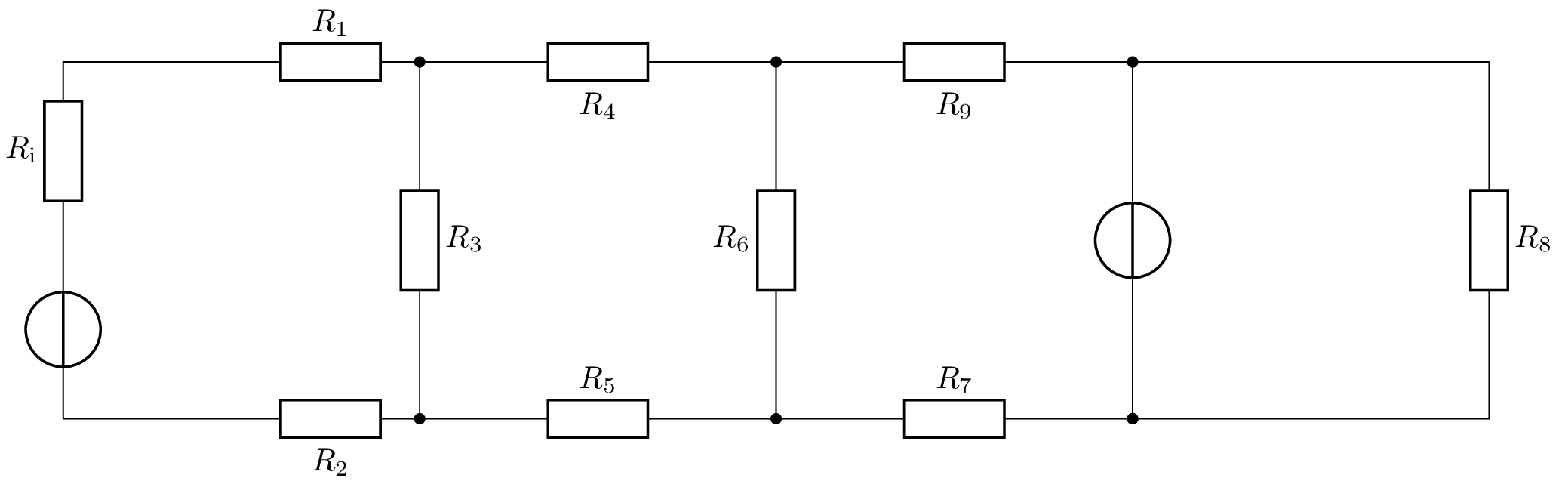
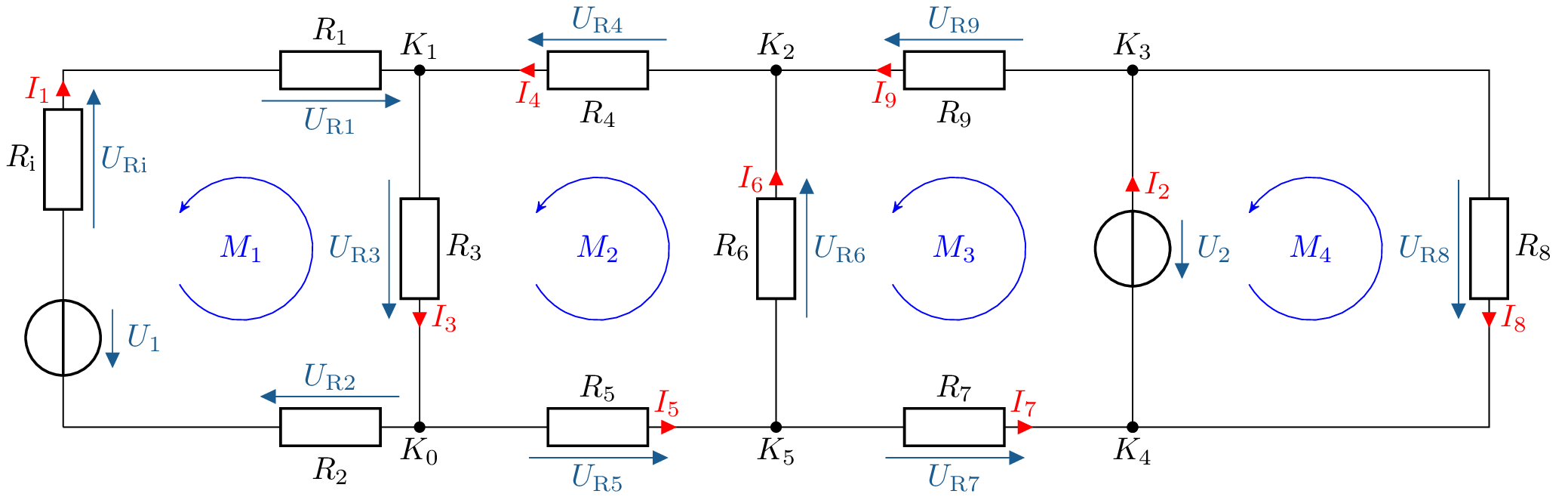
• Netzwerk mit Strömen und Spannungen:
  

  

• Knotengleichungen: \begin {align} K_0 : -I_1+I_3-I_5 &=0 \nonumber \\ K_1 : +I_1-I_3+I_4 &=0 \nonumber \\ K_2 : -I_4+I_6+I_9 &=0 \nonumber \\ K_3 : +I_2-I_8-I_9 &=0 \nonumber \\ K_4 : -I_2-I_7+I_8 &=0 \nonumber \\ K_5 : +I_5-I_6-I_7 &=0 \nonumber \end {align}
• Maschengleichungen: \begin {align} M_1 : U_1-U_\mathrm {Ri}-U_\mathrm {R1}-U_\mathrm {R2}-U_\mathrm {R3} &=0 \nonumber \\ M_2 : U_\mathrm {R3}+U_\mathrm {R4}+U_\mathrm {R5}+U_\mathrm {R6} &=0 \nonumber \\ M_3 : -U_\mathrm {R6}+U_\mathrm {R7}-U_2+U_\mathrm {R9} &=0 \nonumber \\ M_4 : U_2-U_\mathrm {R8} &=0 \nonumber \end {align}

4 Superposition 1

Gegeben ist unten stehendes Netzwerk.

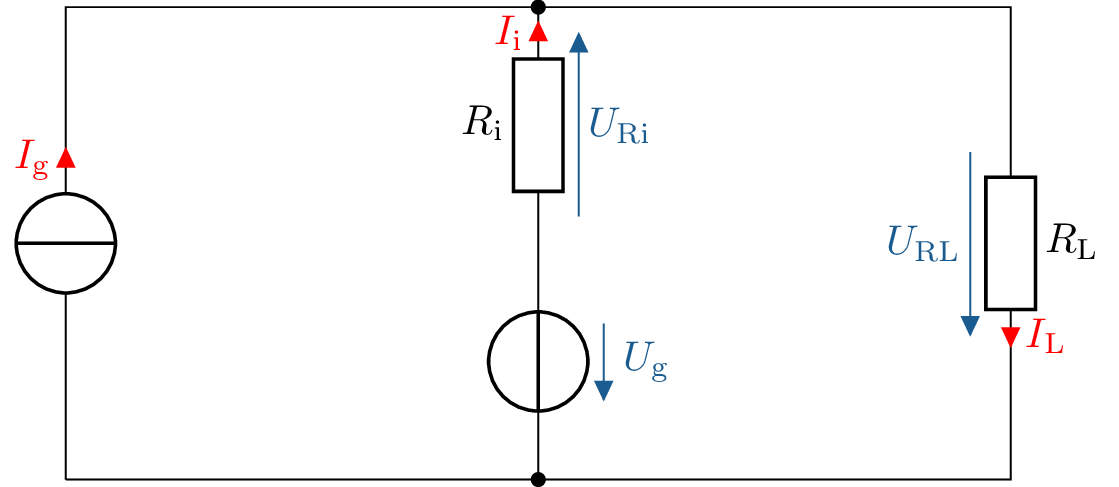
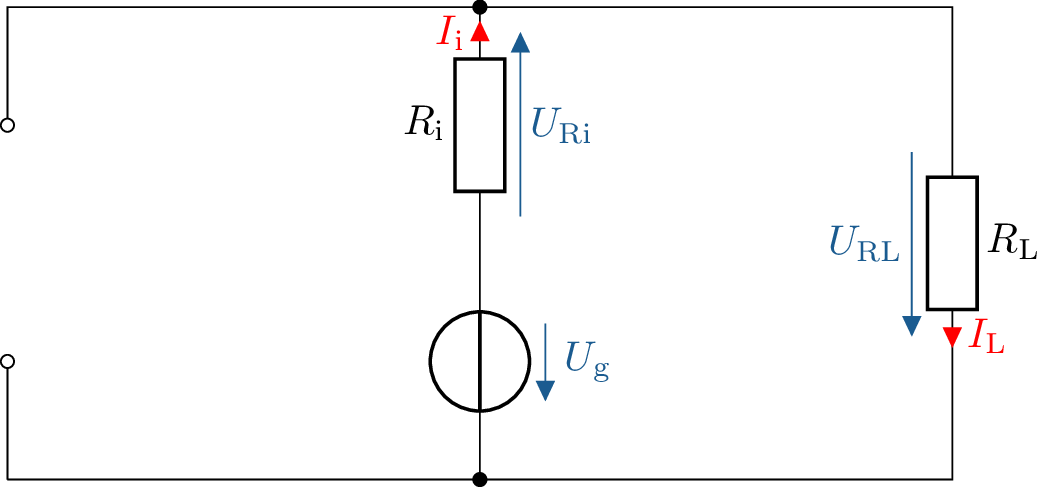
Bestimmen Sie mit Hilfe des Superpositionsverfahrens die Spannung, die über dem Widerstand \(R_L\) abfällt. Befolgen Sie hierzu die folgenden Schritte:

• Bestimmen Sie den Anteil von \(U_g\).
• Bestimmen Sie den Anteil von \(I_g\).
• Führen Sie die Ergebnisse durch den Überlagerungssatz zusammen.

• Anteil von \(U_g\):
  

  

  \begin {equation} U_\mathrm {RL}(U_\mathrm {g}) = \frac {R_\mathrm {L}}{R_\mathrm {i} + R_\mathrm {L}} \cdot U_\mathrm {g} \nonumber \end {equation}

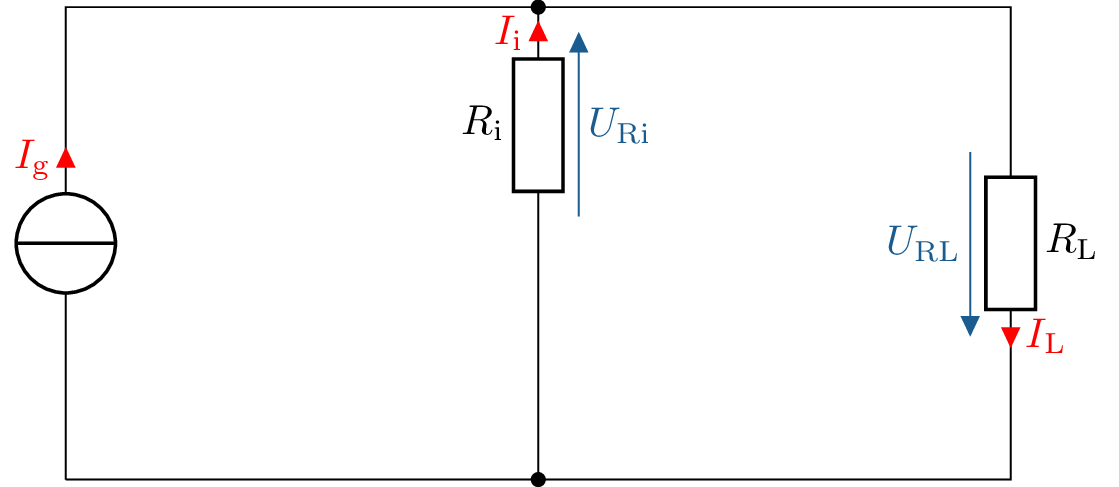
• Anteil von \(I_g\):
  

  

  \begin {equation} U_\mathrm {RL}(I_\mathrm {g}) = \frac {R_\mathrm {i} \cdot R_\mathrm {i}}{R_\mathrm {i} + R_\mathrm {L}} \cdot I_\mathrm {g} \nonumber \end {equation}

• Überlagerungssatz:
  

  \begin {equation} U_\mathrm {RL} = U_\mathrm {RL}(U_\mathrm {g}) + U_\mathrm {RL}(I_\mathrm {g}) = \frac {R_\mathrm {L}}{R_\mathrm {i} + R_\mathrm {L}} \cdot U_\mathrm {g} + \frac {R_\mathrm {i} \cdot R_\mathrm {i}}{R_\mathrm {i} + R_\mathrm {L}} \cdot I_\mathrm {g} \nonumber \end {equation}

5 Knotenpotentialverfahren 1

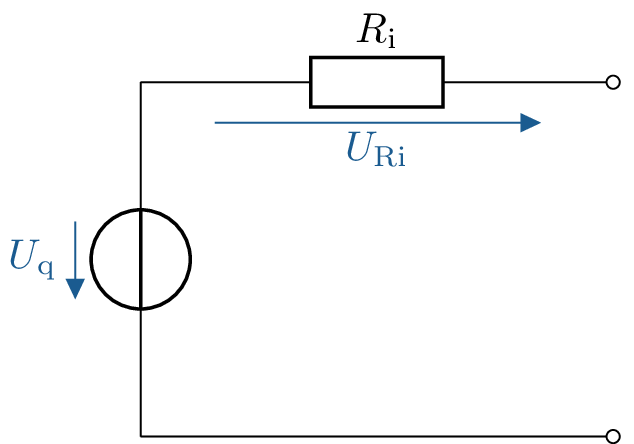
Gegeben ist das Netzwerk einer realen Spannungsquelle \(U_\mathrm {q} = 3,6\ V\) mit einem Innenwiderstand vo \(R_\mathrm {i} = 0,2\ \Omega \).

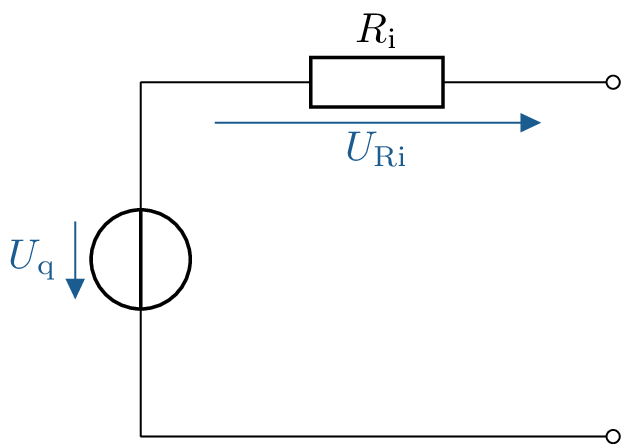
Wandeln Sie die angegebene reale Spannungsquelle in eine reale Stromquelle um. Befolgen Sie hierzu die folgenden Schritte:

• Bestimmen Sie den Leitwert des Widerstandwertes.
• Wandeln Sie die reale Spannungsquelle in eine reale Stromquelle um.
• Berechnen Sie den Stromwert der umgewandelten Stromquelle.

• Leitwert:
  \begin {equation} G_\mathrm {i} = \frac {1}{R_\mathrm {i}} = \frac {1}{0,2\ \Omega } = 5\ \mathrm {S} \nonumber \end {equation}

• Stromquelle:
  

  

• Stromwert:
  \begin {equation} I_\mathrm {q} = U_\mathrm {q} \cdot G_\mathrm {i} = 3,6\ \mathrm {V} \cdot 5\ \mathrm {S} = 72\ \mathrm {A} \nonumber \end {equation}

6 Knotenpotentialverfahren 2

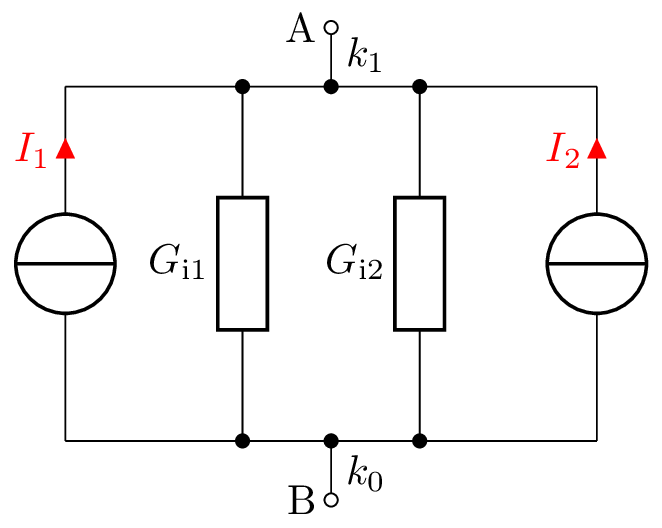
Im folgenden Netzwerk werden zwei parallel verschaltete Ersatzschaltbilder von Batteriezellen dargestellt. Sie bestehen aus den Spannungsquellen \(U_1\) und \(U_2\) sowie den Innenwiderständen \(R_{i1}\) und \(R_{i2}\). Führen Sie die Analyse mit dem Knotenpotentialverfahren durch.

a)

Formen Sie das Netzwerk um, sodass das Knotenpotentialverfahren anwendbar wird.

b)

Stellen Sie die Kontenadmittanzmatrix (KAM) auf.

c)

Stellen Sie den Vektor der Knoteneinströmungen (I) auf.

d)

Lösen Sie das Gleichungssystem und berechnen Sie die Spannung \(U_0\) zwischen den Klemmen \(A\) und \(B\).

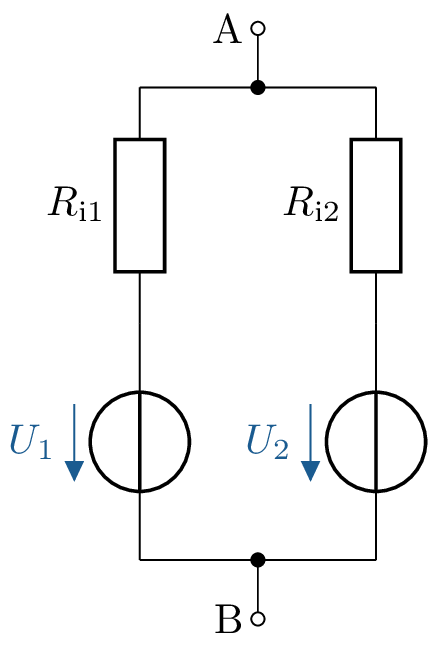
• Umwandlung:

  

  \begin {equation} I_1 = \frac {U_1}{R_\mathrm {i1}} = \frac {0,8\ V}{4,8\ \Omega } = 166\ mA \qquad I_2 = \frac {U_2}{R_\mathrm {i2}} = \frac {1,5\ V}{0,8\ \Omega } = 1,875\ A \nonumber \end {equation}

  \begin {equation} G_\mathrm {i1} = \frac {1}{R_\mathrm {i1}} = \frac {1}{4,8\ \Omega } = 208\ m\Omega \qquad G_\mathrm {i2} = \frac {1}{R_\mathrm {i2}} = \frac {1}{0,8\ \Omega } = 1,25\ \Omega \nonumber \end {equation}

• Kontenadmittanzmatrix:

  \begin {equation} KAM = (G_\mathrm {i1} + G_\mathrm {i2}) = 208\ m\Omega + 1,25\ \Omega \nonumber \end {equation}

• Vektor der Knoteneinströmungen:
  

  \begin {equation} I = (I_1 + I_2) = 166\ mA + 1,875\ A \nonumber \end {equation}

• Gleichungssystem lösen:
  

  \begin {align} KAM \cdot U &= I \nonumber \\ (G_\mathrm {i1} + G_\mathrm {i2}) \cdot U_0 &= (I_1 + I_2) \nonumber \\ (208\ m\Omega + 1,25\ \Omega ) \cdot U_0 &= (166\ mA + 1,875\ A) \nonumber \\ U_0 = \frac {I_1 + I_2}{G_\mathrm {i1} + G_\mathrm {i2}} &= \frac {166\ mA + 1,875\ A}{208\ m\Omega + 1,25\ \Omega } = 1,4\ V \nonumber \end {align}

7 Maschenstromverfahren 1

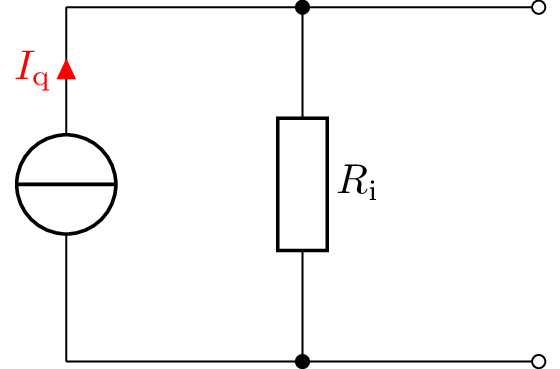
Gegeben ist das Netzwerk einer realen Stromgquelle \(I_\mathrm {q} = 6\ A\) mit einem Leitwert vo \(G_\mathrm {i} = \frac {2}{3}\ S\).

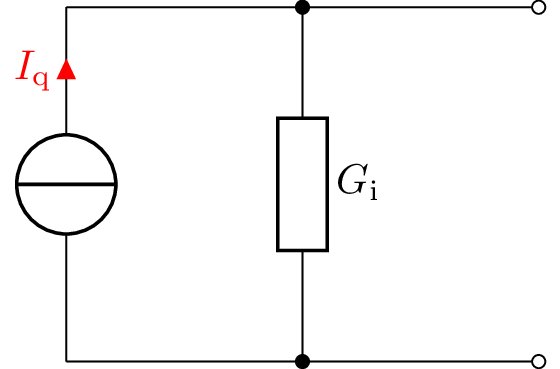
Wandeln Sie die angegebene reale Stromquelle in eine reale Spannungsquelle um. Befolgen Sie hierzu die folgenden Schritte:

• Bestimmen Sie den Widerstandswert des Leitwertes.
• Wandeln Sie die reale Stromquelle in eine reale Spannungsquelle um.
• Berechnen Sie die Spannung der umgewandelten Spannungsquelle.

• Widerstandswert:
  

  \begin {equation} R_\mathrm {i} = \frac {1}{G_\mathrm {i}} = \frac {1}{\frac {2}{3}\ S} = 1,5\ \Omega \nonumber \end {equation}

• Spannungsquelle:
  

  

• Spannungswert
  

  \begin {equation} U_\mathrm {q} = R_\mathrm {i} \cdot I_\mathrm {q} = 1,5\ \mathrm {\Omega } \cdot 6\ \mathrm {A} = 9\ \mathrm {V} \nonumber \end {equation}

8 Maschenstromverfahren 2

Im folgenden Netzwerk wird ein Netzwerk bestehend aus drei Widerständen und zwei Spannungsquellen dargestellt. Führen Sie die Analyse des Netzwerkes mit dem Maschenstromverfahren durch.

Werte: \[ R_1 = 4{,}7\,\text {k}\Omega R_2 = 3{,}3\,\text {k}\Omega R_3 = 2{,}2 \text {k} \Omega U_1 = 24\,\text {V} U_2 = 12\,\text {V} \]

• Vorbereitung des Netzwerkes
• Maschen und Maschenströme definieren
• Widerstandsmatrix bestimmen
• Quellspannungen zuordnen
• Gleichungssystem aufstellen

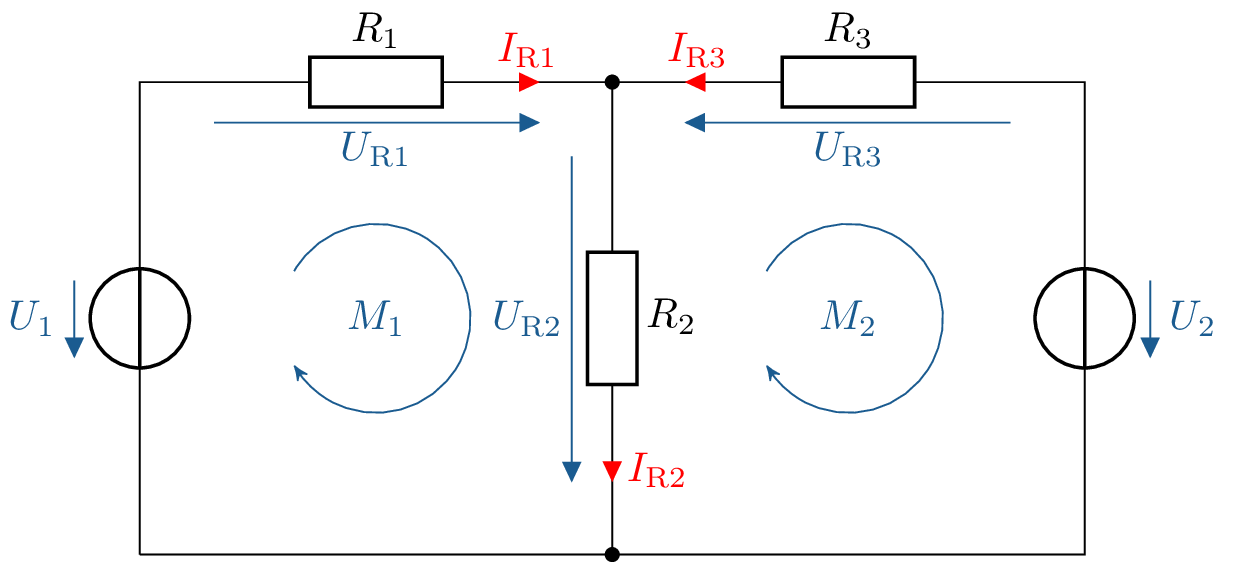
• Vorbereitung des Netzwerkes:
  Das Netzwerk besteht aus:

  • Zwei Spannungsquellen: \(U_1\) und \(U_2\),
  • Drei Widerständen: \(R_1\), \(R_2\), \(R_3\),
  • Drei mögliche Maschen.

  Es sind Spannungsquellen und Widerstandswerte vorhanden.

• Maschen und Maschenströme definieren:
  

  • \(M_1\): Maschenstrom in der linken Masche,
  • \(M_2\): Maschenstrom in der rechten Masche,
  • Der Strom \(I_\mathrm {R2}\) durch \(R_2\) ergibt sich zu: \[ I_\mathrm {R2} = \begin {bmatrix} I_{M1} \\ I_{M2} \end {bmatrix} \]
• Widerstandsmatrix bestimmen: \[ \mathbf {R_M} = \begin {bmatrix} R_1 + R_2 & -R_2 \\ -R_2 & R_2 + R_3 \end {bmatrix} \] Einsetzen der Werte: \[ \mathbf {R_M} = \begin {bmatrix} 4{,}7\ \Omega + 3{,}3\ \Omega & -3{,}3\ \Omega \\ -3{,}3\ \Omega & 3{,}3\ \Omega + 2{,}2\ \Omega \end {bmatrix} = \begin {bmatrix} 8{,}0\ \Omega & -3{,}3\ \Omega \\ -3{,}3\ \Omega & 5{,}5\ \Omega \end {bmatrix} \]
• Quellspannungen zuordnen:
  \begin {equation} \mathbf {U_M} = \begin {bmatrix} U_1 \\ -U_2 \end {bmatrix} = \begin {bmatrix} 24\ V \\ -12\ V \end {bmatrix} \nonumber \end {equation}

• Gleichungssystem aufstellen:
  

  \[ \mathbf {R_M} \cdot \mathbf {I_M} = \mathbf {U_M}, \] wobei: \[ \mathbf {R_M} = \begin {bmatrix} 8{,}0\ \Omega & -3{,}3\ \Omega \\ -3{,}3\ \Omega & 5{,}5\ \Omega \end {bmatrix}, \mathbf {I_M} = \begin {bmatrix} I_{M1} \\ I_{M2} \end {bmatrix}, \mathbf {U_M} = \begin {bmatrix} 24\ V \\ -12\ V \end {bmatrix}. \]

  Das Lösen des Gleichungssystems liefert: \begin {equation} I_{M1} = 2{,}79\,\text {mA} \text {und} I_{M2} = -0{,}507\,\text {mA} \nonumber \end {equation}

  Daraus ergeben sich: \begin {align} I_\mathrm {R1} &= I_\mathrm {M1} = 2,79\ mA \nonumber \\ I_\mathrm {R2} &= I_\mathrm {M1} + (-I_\mathrm {M2}) = 2,79\ mA + 0,507\ mA = 3,297\ mA \nonumber \\ I_\mathrm {R3} &= -I_\mathrm {M2} = 0,507\ mA \nonumber \end {align}

  und

  \begin {align} U_\mathrm {R1} &= R_1 \cdot I_\mathrm {R1} = 4,7\ k\Omega \cdot 2,79\ mA = 13,12\ V \nonumber \\ U_\mathrm {R2} &= R_2 \cdot I_\mathrm {R1} = 3,3\ k\Omega \cdot 3,297\ mA = 10,88\ V \nonumber \\ U_\mathrm {R3} &= R_3 \cdot I_\mathrm {R1} = 2,2\ k\Omega \cdot 0,507\ mA = 1,12\ V \nonumber \end {align}

  Überprüfung der Maschen:

  \begin {align} U_\mathrm {1} &= U_\mathrm {R1} + U_\mathrm {R2} = 24\ V \nonumber \\ U_\mathrm {2} &= U_\mathrm {R2} + U_\mathrm {R3} = 12\ V \nonumber \end {align}