Sprache wählen Icon

Elektromagnetismus

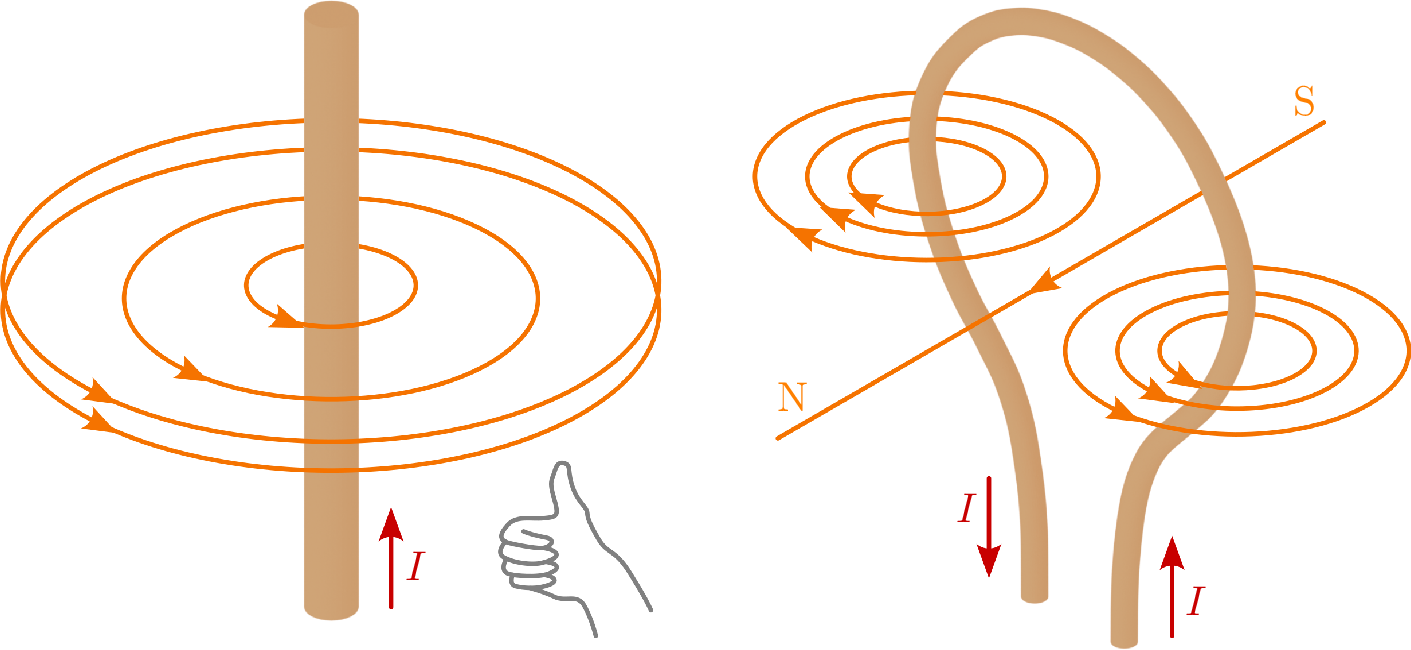
Ein magnetisches Feld kann außer durch einen Permanentmagneten, auch durch einen elektrischen Strom erzeugt werden. Dabei ergibt sich ein kreisförmiges magnetisches Feld um den stromdurchflossenen Leiter. Die Richtung des Feldes lässt sich mit der „rechten Hand Regel“ ermittelt werden: Bei einer zur Faust geformten rechten Hand mit gestrecktem Daumen zeigt der Daumen in Richtung des (technischen) elektrischen Stromflusses (der „technische Stromfluss“ verläuft vom Plus- zum Minuspol) und die Finger in Richtung des magnetischen Feldlinienverlaufs.  

Merke: Rechte Hand Regel

Zeigt der Daumen der rechten Hand in Richtung des (technischen) elektrischen Stromflusses, so zeigen die restlichen gebeugten Finger die Verlaufsrichtung der magnetischen Feldlinien an.

Zwei schematische Darstellungen von stromdurchflossenen Leitern. Links ist ein gerader Draht zu sehen, durch den ein elektrischer Strom (I) fließt, dargestellt durch einen roten Pfeil. Um den Draht sind konzentrische magnetische Feldlinien gezeichnet, die die Richtung des Magnetfeldes angeben. Mithilfe der Rechten-Hand-Regel lässt sich abhängig von der Richtung, in der der Strom den Leiter durchfließt, die Richtung des Magnetfeldes bestimmen. Rechts sieht man einen Draht, der eine Schleife bildet. Auch hier fließt der elektrische Strom (I), und das Magnetfeld wird durch kreisförmige Linien um die Schleife herum dargestellt. Die Polarität des Magnetfeldes wird durch die Buchstaben ’N’ (Nordpol) und ’S’ (Südpol) angezeigt. Die Richtung der Magnetfeldlinien wird durch Pfeile entlang der Linien verdeutlicht.

Abbildung 1: Magnetisches Feld um einen stromdurchflossenen Leiter. Links: Die Richtung des Feldes kann mit der „rechten Hand Regel“ veranschaulicht werden. Rechts: Die Leiterschleife stellt die kleinste Einheit einer Spule dar. Die hier dargestellte mittlere Feldlinie schließt sich in der Unendlichkeit.

1 Durchflutung

Die durch elektrische Ströme hervorgerufenen Magnetfelder werden mit der Kenngröße der magnetischen Durchflutung \(\varTheta \) (Theta) beschrieben. Analog zur elektrischen Spannung wird die Durchflutung auch als magnetische Spannung bezeichnet. Da die Durchflutung proportional zum Strom ist, hat sie wie der Strom die Einheit Ampere.

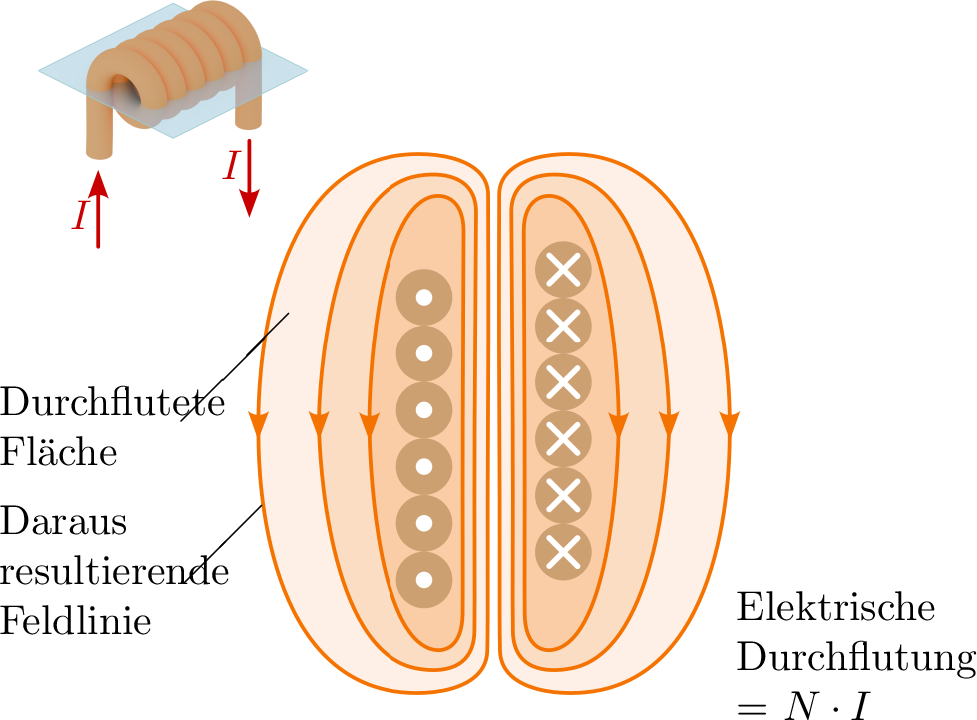
Der Name ist auf das Durchflutungsgesetz zurückzuführen. Dieses besagt, dass die magnetische Durchflutung \(\varTheta \) gleich dem Gesamtstrom \(I\) ist, der durch die von der betrachteten geschlossenen Linie umschlossene Fläche fließt (siehe Abbildung 2). Die Gleichung 1 gibt das Durchflutungsgesetz in der allgemeinen Form wieder. Die rechte Seite bezeichnet das Flächenintegral der Stromdichte \(\vec {J}\). Dieses Integral drückt die Summe des Stromes aus, der durch die Fläche \(A\) fließt. Die linke Seite der Gleichung stellt das geschlossene Linienintegral über die magnetische Feldstärke \(\vec {H}\) dar. Diese geschlossene Linie \(\mathrm{d} \vec {s}\) entspricht dabei dem Rand der Fläche \(A\).

\begin {equation} \varTheta = \oint _s \vec {H}\cdot \mathrm{d} \vec {s} = \iint _A \vec {J}\,\mathrm{d} \vec {A}\label {Durchflutung} \end {equation}

Da in den allermeisten Fällen der Strom durch einen Leiter transportiert wird und folglich die Richtung des Stromes als auch die Stromstärke eindeutig bekannt sind, genügt es in diesem Fall, das Integral (wie in der Gleichung 2 dargestellt) durch die Anzahl der stromführenden Leiter \(N\) multipliziert mit der Stromstärke \(I\) zu ersetzen.

\begin {equation} \varTheta = \oint _s \vec {H}\cdot \mathrm{d} \vec {s} = N\cdot I\label {Durchflutungsgesetz} \qquad [\mathrm {A}] \end {equation}

Merke: Magnetische Durchflutung

Die magnetische Durchflutung \(\varTheta \) entspricht dem Gesamtstrom einer von ihm durchfluteten Fläche.

Ein Diagramm zur elektrischen Durchflutung einer Spule. Oben wird eine Drahtspule dargestellt, durch die ein elektrischer Strom fließt, gekennzeichnet durch die Pfeile Ï”für den Stromfluss. Darunter ist der Querschnitt einer Drahtspule zu sehen, zusammen mit den Magnetfeldlinien, die durch den Stromfluss an der Spule erzeugt werden. Innerhalb der magnetfeldlinien sind die durchfluteten Flächen farbig hinterlegt.

Abbildung 2: Durchflutung einer Spule. Die Durchflutung entspricht dem Gesamtstrom durch eine durchflutete Fläche. Die elektrische Durchflutung einer Spule ist daher abhängig von der Wicklungszahl und der Stromstärke. Für die Darstellung in einer zweidimensionalen Grafik wird das Symbol \(\otimes \) für den Stromfluss „in die Bildfläche hinein“, \(\odot \) für „aus der Bildfläche heraus“ verwendet.

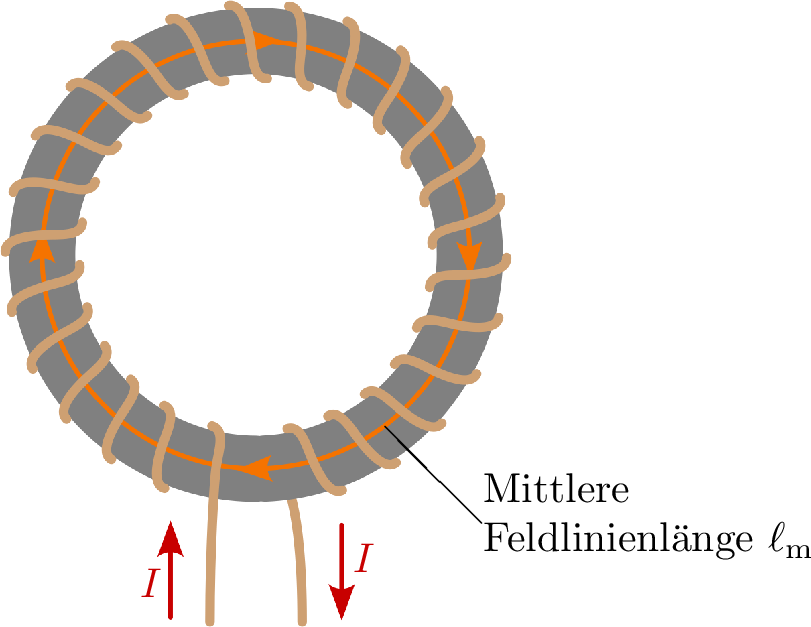
Ist die magnetische Feldstärke über dem Integrationsweg \(\mathrm{d} \vec {s}\) konstant, kann der Vektor \(\vec {H}\) vor das Integral gezogen werden. Diese Bedingung ist in der Regel erfüllt, wenn sich die Feldlinie über dem ganzen Integrationsweg im gleichen Material befindet. Ein Beispiel wäre ein kreisförmiges Feld um einen Leiter im Kreismittelpunkt oder eine Ringkernspule, wie in Abbildung 3 gezeigt. In dem Fall wird das Integral \(\oint \vec {H}\cdot \,\mathrm{d} \vec {s}\) zur Länge des Integrationsweges (Gleichung ??). Diese Länge wird mittlere Feldlinienlänge genannt und mit \(\ell _{\mathrm {m}}\) bezeichnet. Sie steht für den Mittelwert der Summe aller Feldlinien, die sich innerhalb des kreisförmigen Feldes befinden. Die magnetische Feldstärke kann in solchen Anordnungen einfach mit der Gleichung ?? ermittelt werden.

\begin {align} \varTheta &= \oint _s \vec {H}\cdot \mathrm{d} \vec {s} = |\vec {H}| \cdot \ell _{\mathrm {m}}\label {GlmagnFeldstaerke}\\ |\vec {H}| &=\frac {\varTheta }{\ell _{\mathrm {m}}}\qquad \left [\frac {\mathrm {A}}{\mathrm {m}}\right ]\label {GlmagnFeldstaerke1} \end {align}

Merke: Berechnungshilfe magnetische Feldstärke

Ist die magnetische Feldstärke über den ganzen Weg konstant, kann sie durch den Quotienten von Durchflutung \(\varTheta \) und Weglänge \(\ell _{\mathrm {m}}\) berechnet werden. Ihre Einheit ist Ampere pro Meter.

Grafik eines ringförmigen Spulenkerns, der mit Drahr umwickelt ist. Zwei Pfeile an den Enden der Drähte weisen in entgegengesetzte Richtungen und symbolisieren die Flussrichtung des elektrischen Strom (I). Innderhalb des Rings ist die mittlere Feldlinienlänge (lm) mit deren Flussrichtung eingezeichnet. Die mittlere Feldlinie befindet sich in der Mitte des ringfärmigen Spulenkerns.

Abbildung 3: Ringkernspule mit mittlerer Feldlinienlänge. Die mittlere Feldlinienläge repräsentiert den Mittelwert aller Feldlinien innerhalb der Spule, womit die Feldstärke einfach rechnerisch ermittelt werden kann.

Beispiel 1: Magnetische Feldstärke über die mittlere Feldlinienlänge

Eine Ringspule (Abbildung 3) mit \(1000\) Windungen und einer mittleren Feldlinienlänge von \(50\,\mathrm {cm}\) wird von einer Stromstärke von \(100\,\mathrm {mA}\) durchflossen. Wie groß ist die magnetische Feldstärke?\begin {align} \varTheta &= H \cdot \ell _{\mathrm {m}} = N\cdot I\nonumber \\ H&=\frac {N\cdot I}{\ell _{\mathrm {m}}} =\frac {1000\cdot 0,1\,\mathrm {A}}{0,5\,\mathrm {m}} = 200\,\tfrac {\mathrm {A}}{\mathrm {m}}\nonumber \end {align}

Beispiel 2: Magnetische Feldstärke über den Kreisumfang

Ein gerader Leiter wird mit einem Strom von \(I=50\,\mathrm {A}\) durchflossen. Wie groß ist die magnetische Feldstärke in einem Abstand von \(r=20\,\mathrm {cm}\)? \begin {equation*} H=\frac {N\cdot I}{\ell _{\mathrm {m}}} =\frac {1\cdot 50\,\mathrm {A}}{2\pi \cdot 0,2\,\mathrm {m}} = 39,79\,\tfrac {\mathrm {A}}{\mathrm {m}} \end {equation*} Die mittlere Feldlinienlänge \(\ell _{\mathrm {m}}\) kann durch den Kreisumfang ermittelt werden und wird deshalb mit der Formel zur Berechnung des Kreisumfangs \(2\pi \cdot r\) ersetzt.

Expand
×

...