Magnetischer Fluss und Flussdichte

Der magnetische Fluss ist analog zum elektrischen Kreis mit dem Strom vergleichbar. Entgegen der Terminologie findet jedoch kein Fluss von magnetischen Teilchen statt, sondern er ist sinnbildlich als „die Menge an Magnetfeld“ zu verstehen und wirkt in Folge der magnetischen Spannung. Das Formelzeichen des magnetischen Flusses ist \(\varPhi \), die Einheit ist Weber (Wb). Ein Weber (Wb) ist gleichbedeutend mit einer Volt-Sekunde (Vs).

Die Kraftwirkung eines Magneten ist abgesehen vom magnetischen Fluss auch von der durchfluteten Fläche abhängig. Je dichter die Feldlinien konzentriert sind, desto größer ist die magnetische Wirkung. Das wird durch die magnetische Flussdichte \(B\) beschrieben, die im einfachsten Fall (nicht gekrümmte Fläche, homogene Flussdichte) durch den Quotienten aus dem magnetischen Fluss \(\varPhi \) und der Fläche \(A\) definiert ist. Die Einheit der Flussdichte ist Tesla (T). Die Richung der Flussdichte \(\vec {B}\) ist senkrecht zur Fläche, was durch den Normalenvektor zur Fläche \(\vec {A}\) ausgedrückt wird.

\begin {equation} \vec {B} = \frac {\varPhi }{\vec {A}}\qquad [\mathrm {T}] \end {equation}

Im allgemeinen Fall (ohne die oben genannten Einschränkungen) gilt:

\begin {equation} \varPhi = \iint _A \vec {B}\cdot \mathrm {d}\vec {A} \label {magnFlussFormel} \end {equation}

Sowohl die magnetische Feldstärke als auch die magnetische Flussdichte sind vektorielle Größen. Sie lassen sich daher grafisch durch Feldlinien zeichnen. Der magnetische Fluss \(\varPhi \) ist dagegen eine skalare Größe.

Die magnetische Flussdichte \(\vec {B}\) und die magnetische Feldstärke \(\vec {H}\) sind über die Permeabilität \(\mu \) verbunden. Die Permeabilität besteht aus dem Produkt einer materialunabhängigen Kenngröße, der magnetischen Feldkonstanten \(\mu _0=1,256\,637\,062\cdot 10^{-6}\,\frac {\mathrm {Vs}}{\mathrm {Am}}\), und einer materialspezifischen Permeabilität \(\mu _{\mathrm {r}}\). Die magnetische Feldkonstante beschreibt die Permeabilität im Vakuum und war bis zur Neuordnung der SI-Einheiten im Jahr 2019 mit dem Wert \(\mu _0 = 4\pi \cdot 10^{-7}\,\frac {\mathrm {Vs}}{\mathrm {Am}}\) genau definiert. Jetzt ist sie mit einer Messunsicherheit behaftet.

\begin {equation} \vec {B} = \mu _0\cdot \mu _{\mathrm {r}}\cdot \vec {H}\label {GlFlussdichte} \end {equation}

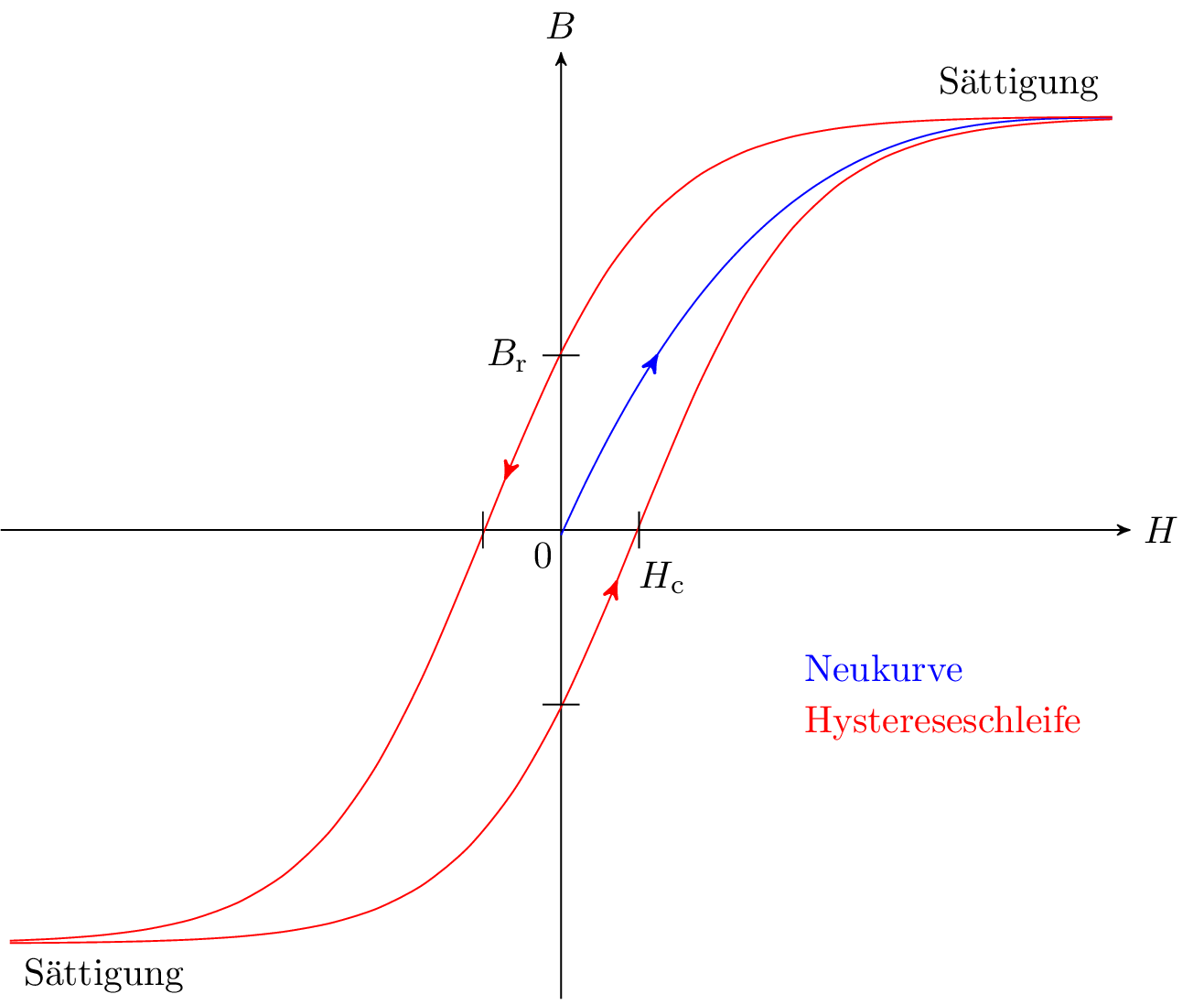
In einem ferromagnetischen Material verläuft der Zusammenhang zwischen der magnetischen Feldstärke \(\vec {H}\) und der magnetischen Flussdichte \(\vec {B}\) nicht linear. Die Permeabilität geht mit steigender Magnetisierung in Sättigung, sodass die relative Permeabilität \(\mu _{\mathrm {r}}\) von einem materialabhängigen Anfangswert gegen 1 läuft. Wird das magnetische Feld wieder reduziert (oder auf Null gesetzt), bleibt die Magnetisierung in einem gewissen Maße erhalten (Punkt \(B_{\mathrm {r}}\) in Abbildung 1). Dieser Vorgang wird Remanenz genannt. Die verbleibende magnetische Flussdichte bei einer magnetischen Feldstärke von Null ist die Remanenzflussdichte \(B_{\mathrm {r}}\). Um den Stoff wieder komplett zu untmagnetisieren, wird eine umgekehrte magnetische Feldstärke, die Koerzitivfeldstärke \(H_{\mathrm {c}}\), benötigt.

Anhand der Koerzitivfeldstärke werden ferromagnetische Materialien in hart- und weichmagnetische Materialien unterschieden. Hartmagnetische Werkstoffe (z. B. starke Dauermagnete aus Neodym-Eisen-Bor) verfügen dabei über einen Wert für \(H_{\mathrm {c}}\) größer als \(10\cdot 10^{3}\,\frac {\mathrm {A}}{\mathrm {m}}\), bei weichmagentischen Werkstoffen (z. B. Magnetkerne aus Mangan-Zink-Ferrit) liegt \(H_{\mathrm {c}}\) bei kleiner als \(500\,\frac {\mathrm {A}}{\mathrm {m}}\). Hartmagnetische Werkstoffe werden hauptsächlich für Permanentmagnete eingesetzt.

Der magnetische Widerstand

Im Kapitel ?? wurde bereits die magnetische Spannung thematisiert, die auch Durchflutung genannt wird, sowie im Kapitel der magnetische Fluss, der das Äquivalent zum elektrischen Strom darstellt. Es liegt daher die Vermutung nahe, dass es in einem magnetischen Kreis äquivalent zum ohmschen Widerstand auch einen magnetischen Widerstand gibt. Er hat das Formelzeichen \(R_{\mathrm {m}}\) und die Einheit \(\frac {\mathrm {A}}{\mathrm {V}\mathrm {s}}\) und wird auch Reluktanz genannt.

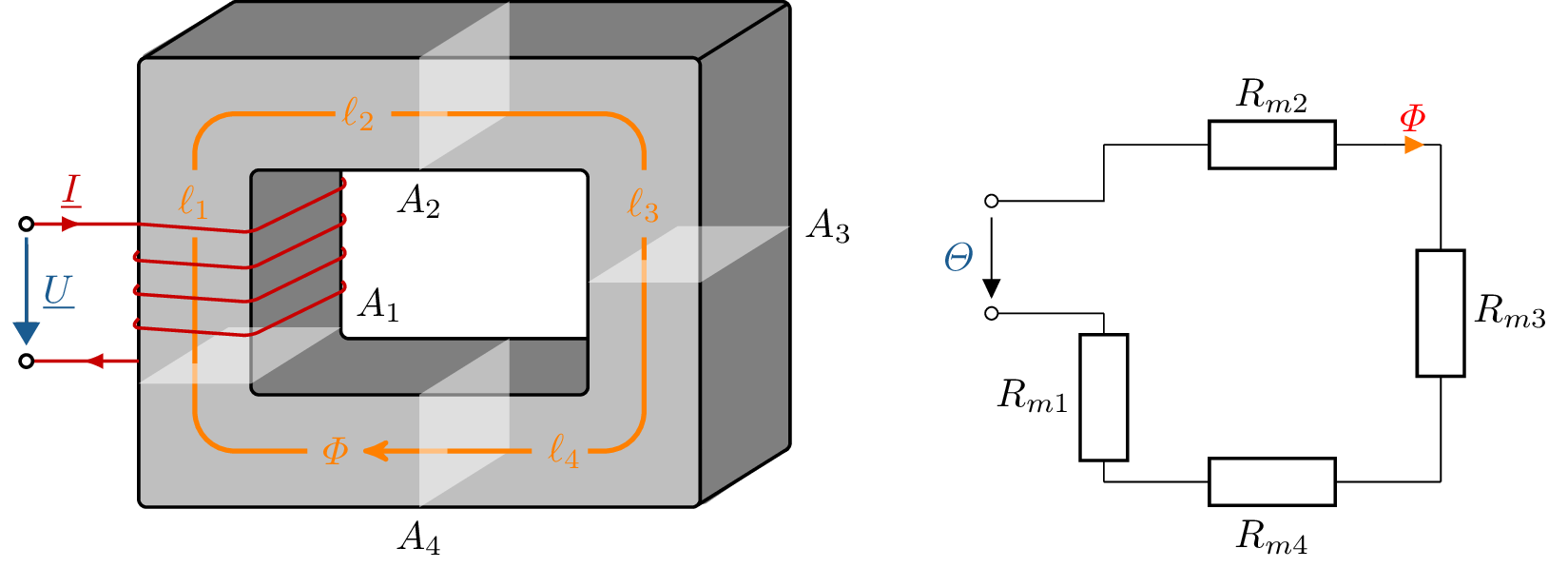
Ein Beispiel für einen magnetischen Kreis ist in Abbildung 1 durch einen einfachen Eisenring mit einer einseitigen Spule dargestellt. Die Spule erzeugt eine Durchflutung \(\varTheta \) analog zur elektrischen Spannung. Der Eisenkreis besteht aus vier Teilwiderständen, da der magnetische Widerstand sowohl von der Länge als auch von dem durchflossenen Querschnitt abhängig ist. Die vier Widerstände werden vom magnetischen Fluss \(\varPhi \) durchströmt.

In einfachen Anordnungen (wie beispielsweise in Abbildung 1 zu sehen) kann unter Vernachlässigung der Ecken der Widerstand durch die Gleichung 1 ausgedrückt werden. \(\ell _{\mathrm {m}}\) ist wie bei der magnetischen Feldstärke die mittlere Feldlinienlänge des Widerstandes innerhalb des magnetischen Kreises. Zur Ermittlung der mittleren Feldlininenlänge \(\ell _{\mathrm {m}}\) werden die Längen aller Seiten addiert. \(A\) ist die Querschnittsfläche, die vom magnetischen Fluss durchflossen wird. \(\mu \) ist die Permeabilität des Materials. Der magnetische Widerstand \(R_{\mathrm {m}}\) berechnet sich nun aus der aufsummierten Länge der mittleren Feldlinienlänge \(\ell _{\mathrm {m}}\) geteilt durch das Produkt der durchflossenen Querschnittsfläche \(A\) und der Permeabilität \(\mu _{\mathrm {r}} \cdot \mu _0\).

\begin {equation} R_{\mathrm {m}} =\frac {\ell _{\mathrm {m}}}{\mu _{\mathrm {r}}\cdot \mu _0\cdot A} \qquad \left [\frac {\mathrm {A}}{\mathrm {V}\cdot \mathrm {s}}\right ]\label {GlmagnWiderstand} \end {equation}

1 Der magnetische Kreis

Werden nun alle bekannten magnetischen Größen in ihrer Zusammenwirkung betrachtet, ergibt sich die magnetische Analogie zum Ohmschen Gesetz. Sie beschreibt, dass die magnetische Spannung \(\varTheta \) dem Produkt aus dem magnetischen Widerstand \(R_{\mathrm {m}}\) und dem magnetischen Fluss \(\varPhi \) entspricht. \begin {align} \varTheta &= R_{\mathrm {m}}\cdot \varPhi \end {align}