Sprache wählen Icon

Lorentzkraft

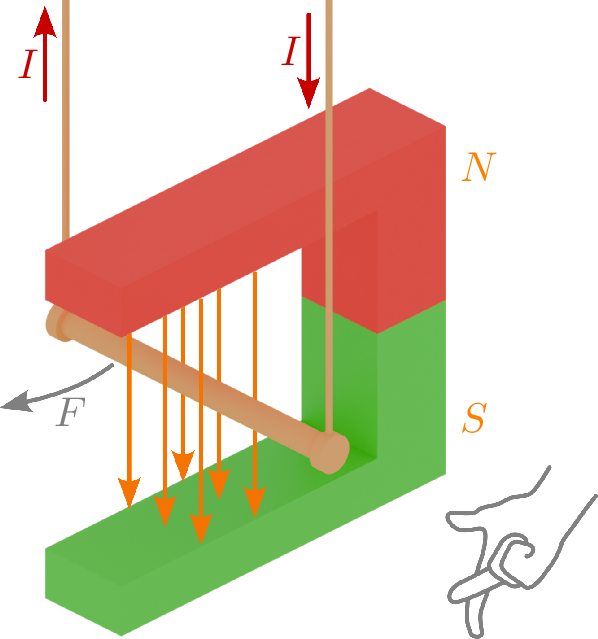
Befindet sich in einem Magnetfeld ein Leiter, der mit Strom durchflossen wird, wirkt auf ihn eine Kraft, die senkrecht zum Leiter und dem Magnetfeld steht. Diese Kraft wird Lorentzkraft genannt. Verläuft der Leiter senkrecht zu den magnetischen Feldlinien, ist die Kraft am größten.

Links ist ein C-förmiger Permanentmagnet abgebildet, der in rot (oberer Teil) und grün (unterer Teil) eingefärbt ist. In der Mitte befindet ein Draht innerhalb des Magnetfeldes des Magneten. Der Draht ist freischwingentd an zwei Zuleitungen aufgehängt. An den Zuleitungen sind Pfeile eingezeichnet, die die Richtung des elektrischen Stroms (I) anzeigen. Die Richtung des Stromflusses bewirkt, dass der freischlingende Leiter innerhalb des Magnetfeldes durch die Lorenzkraft (F) nach vorn abgelenkt wird. Rechts ist eine Hand dargestellt, deren Mittelfinger in Richtung der Lorenzkraft zeigt. Der Daumen zeigt in die Richtung, in die der Strom (I) durch den Draht innerhalb des Magnetfeldes fließt. Der Zeigefinger zeigt nach unten, in die Richtung in die das Magnetfeld (B) wirkt.

Abbildung 1: Versuchsaufbau zur Lorentzkraft. Ablenkung eines freischwingenden stromdurchflossenen Leiters im Feld eines Permanentmagneten, wodurch sich der Leiter in die Richtung der Kraft bewegt. Die Richtung kann mit der Drei-Finger-Regel der rechten Hand bestimmt werden. Der Daumen orientiert sich dabei an der Richtung des Stromflusses, der Zeigefinger an der Richtung der magnetischen Feldlinien. Der Mittelfinger zeigt dann in die Richtung, in die die Kraft wirkt.

Schrittweise Erklärung zum in Abbildung 1 gezeigten Versuchsaufbau mit einem stromdurchflossenen Leiter im Feld eines Permanentmagneten:

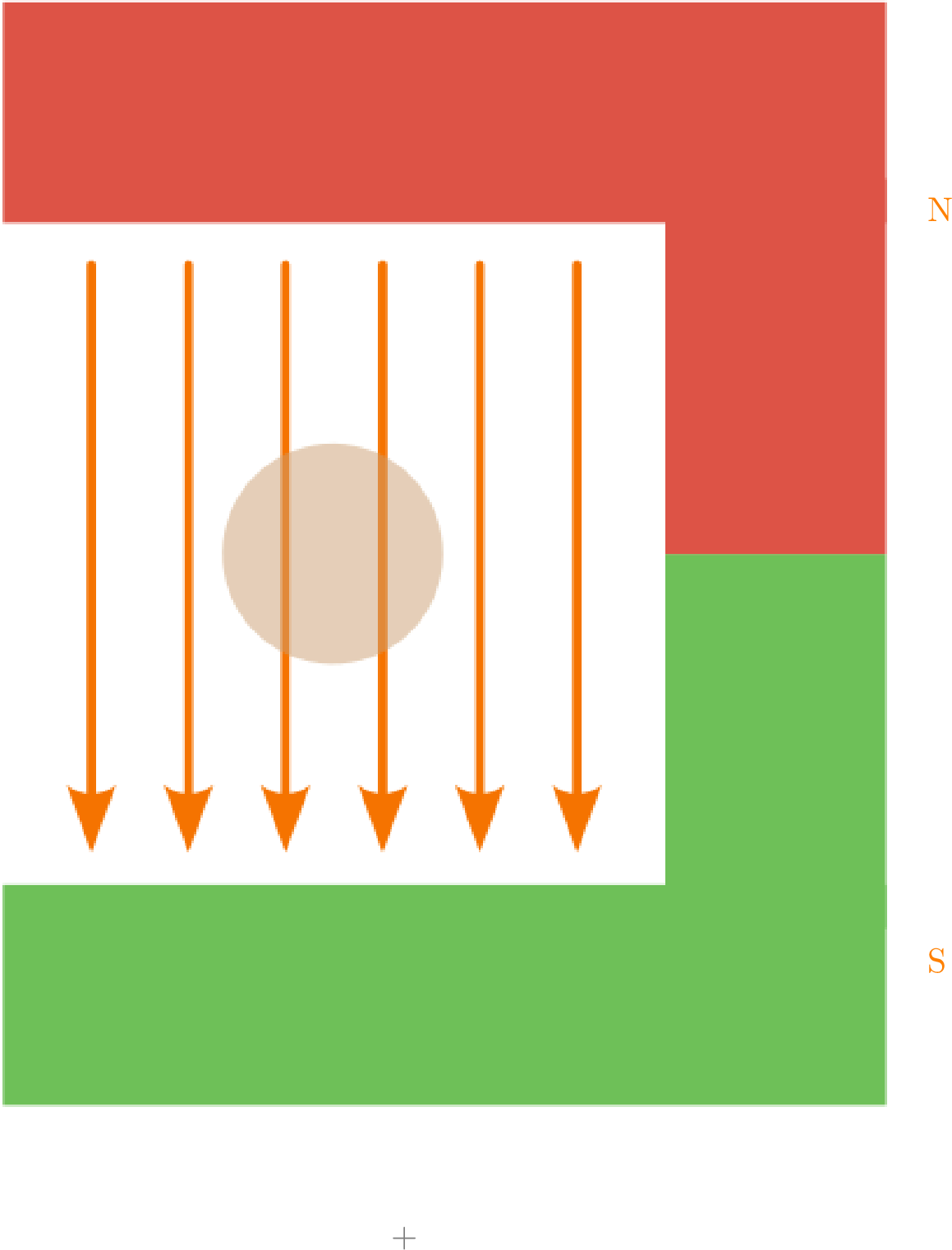
Ein C-förmiger Permanentmagnet ist zu sehen, dessen Magnetfeld vom N-Pol zum S-Pol (von oben nach unten) verweist. Ein Leiter, der sich innerhalb des Magnetfeldes befindet, ist transparent abgebildet und wird ignoriert, da er nicht stromdurchflossen ist.

  • Ein Leiter befindet sich zwischen den Polen eines Hufeisenmagneten.
  • Der Leiter ist hier nicht stromdurchflossen, sodass das Feld des Permanentmagneten einzeln betrachtet werden kann.
  • Die Magnetfeldlinien verlaufen außerhalb des Permanentmagneten vom Nord- zum Südpol und schließen sich innerhalb des Magneten.

Der C-förmige Permanentmagnet ist transparent abgebildet und wird nun ignoriert. Der Leiter, der nun stromdurchflossen ist bildet ein Magnetfeld in Richtung des Uhrzeigersinns um den Leiter.

  • Nun wird der Leiter stromdurchflossen betrachtet, ohne das Feld des Permanentmagneten zu berücksichtigen.
  • Um den stromdurchflossenen Leiter entsteht ein magnetisches Feld in Abhängikeit der Flussrichtung des Stroms (Rechte-Hand-Regel).

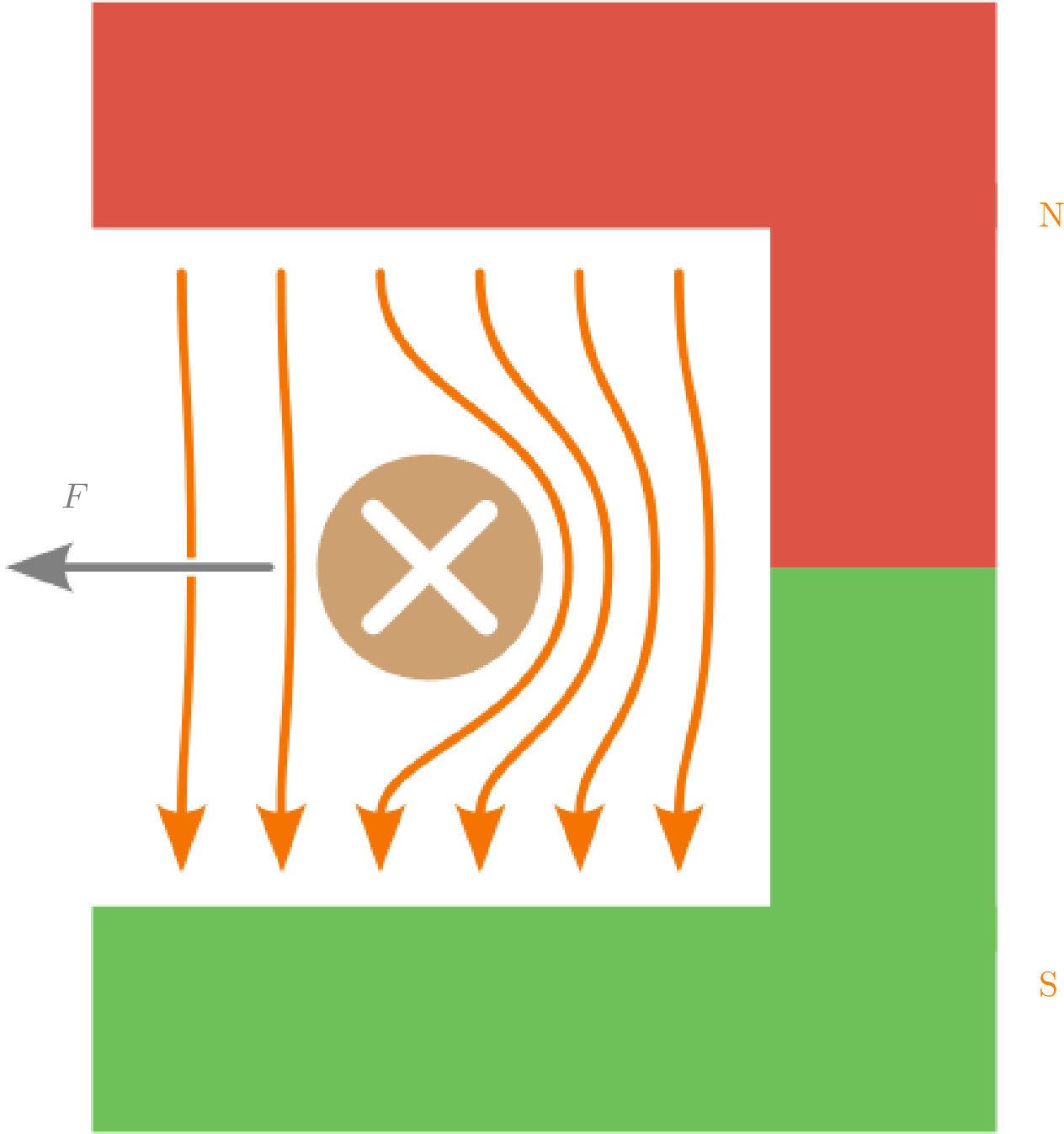
Das Magnetfeld des C-förmigen Permanentmagneten und das Magnetfeld des stromdurchflossenen Leiters werden zusammen betrachtet. Das Magnetfeld des Leiters lenkt das Magnetfeld des Permanentmagneten in deren Zusammenspiel ab, sodass eine Kraft nach links entsteht, da die Magnetfeldlinien des Permanentmagneten rechts herum um den stromdurchflossenen Leiter abgelenkt werden.

  • Das Feld des Permanentmagneten und das magnetische Feld des stromdurchflossenen Leiters werden nun zusammen betrachtet.
  • Beide Felder überlagern sich, sodass auf der Rechten Seite eine Feldverstärkung und links eine Feldschwächung auftritt.
  • Das System versucht diese Feldverzerrung auszugleichen, wodurch eine Kraft auf den Leiter wirkt, die senkrecht zum Leiter und dem Magnetfeld steht (Drei-Finger-Regel).
  • Der Leiter bewegt sich in die Richtung, in die die Kraft wirkt.

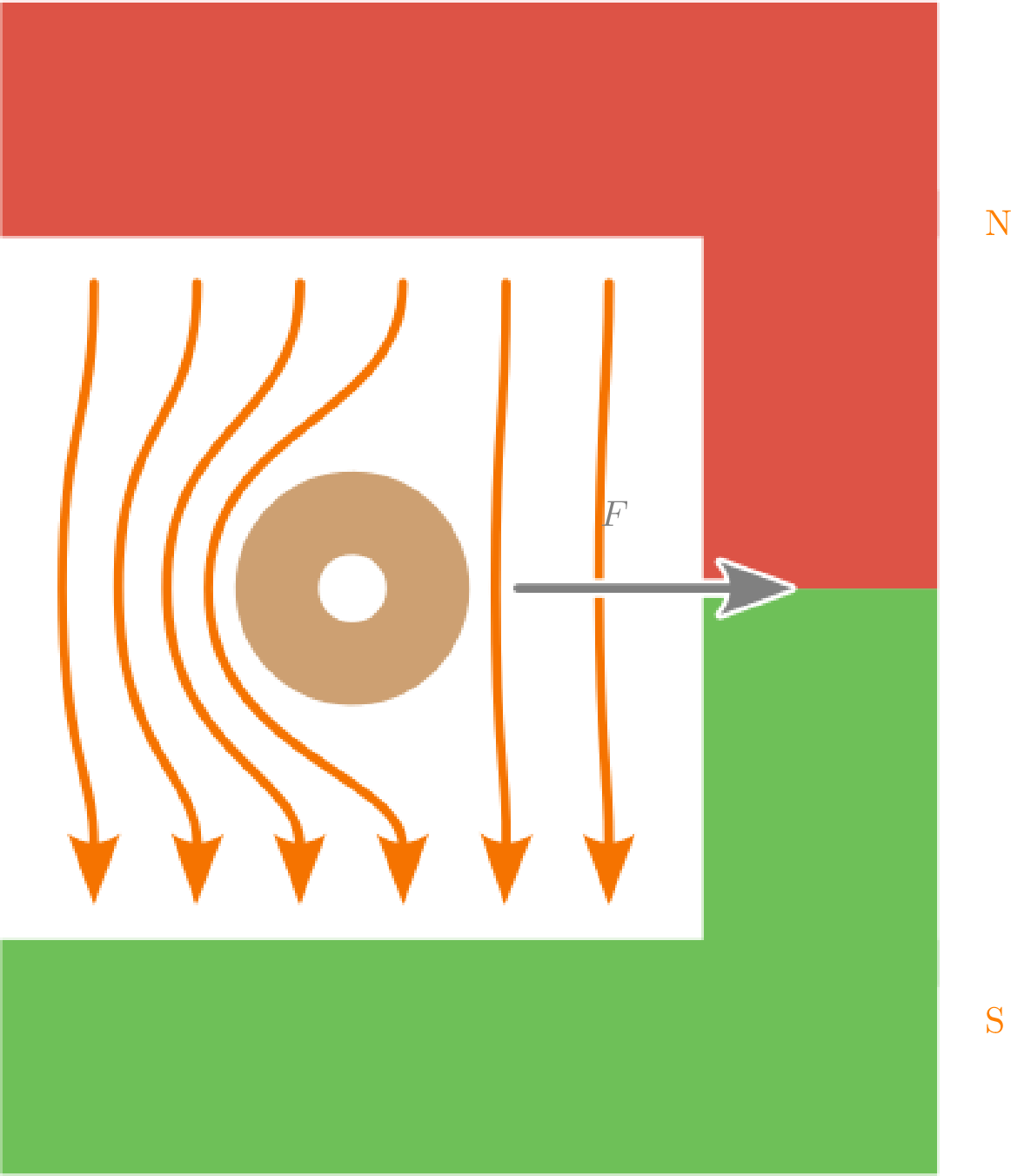
Wird die Flussrichtung des Stromes, der am Leiter anliegt, umgekehrt, ändert sich die Richtung der Kraftwirkung. Der stromdurchflossene Leiter wird nach rechts abgelenkt.

  • Hier wird die Flussrichtung des stromdurchflossenen Leiters umgekehrt.
  • Die Lorentzkraft wirkt entsprechend in die umgekehrte Richtung (Drei-Finger-Regel).
  • Der Leiter bewegt sich in die Richtung, in die die Kraft wirkt.

Zur Berechnung der Lorentzkraft kann die vektorielle oder die skalare Darstellung genutzt werden. Bei der vektoriellen Berechnung (Gleichung ??) bewirkt eine bewegte Einheitsladung \(q\) mit der Geschwindigkeit \(\vec {v}\) im Magnetfeld \(\vec {B}\) die Kraft \(\vec {F}\): \begin {align} \vec {F} = q \cdot (\vec {v} \times \vec {B}) \label {GlLorentzkraftvek} \end {align}

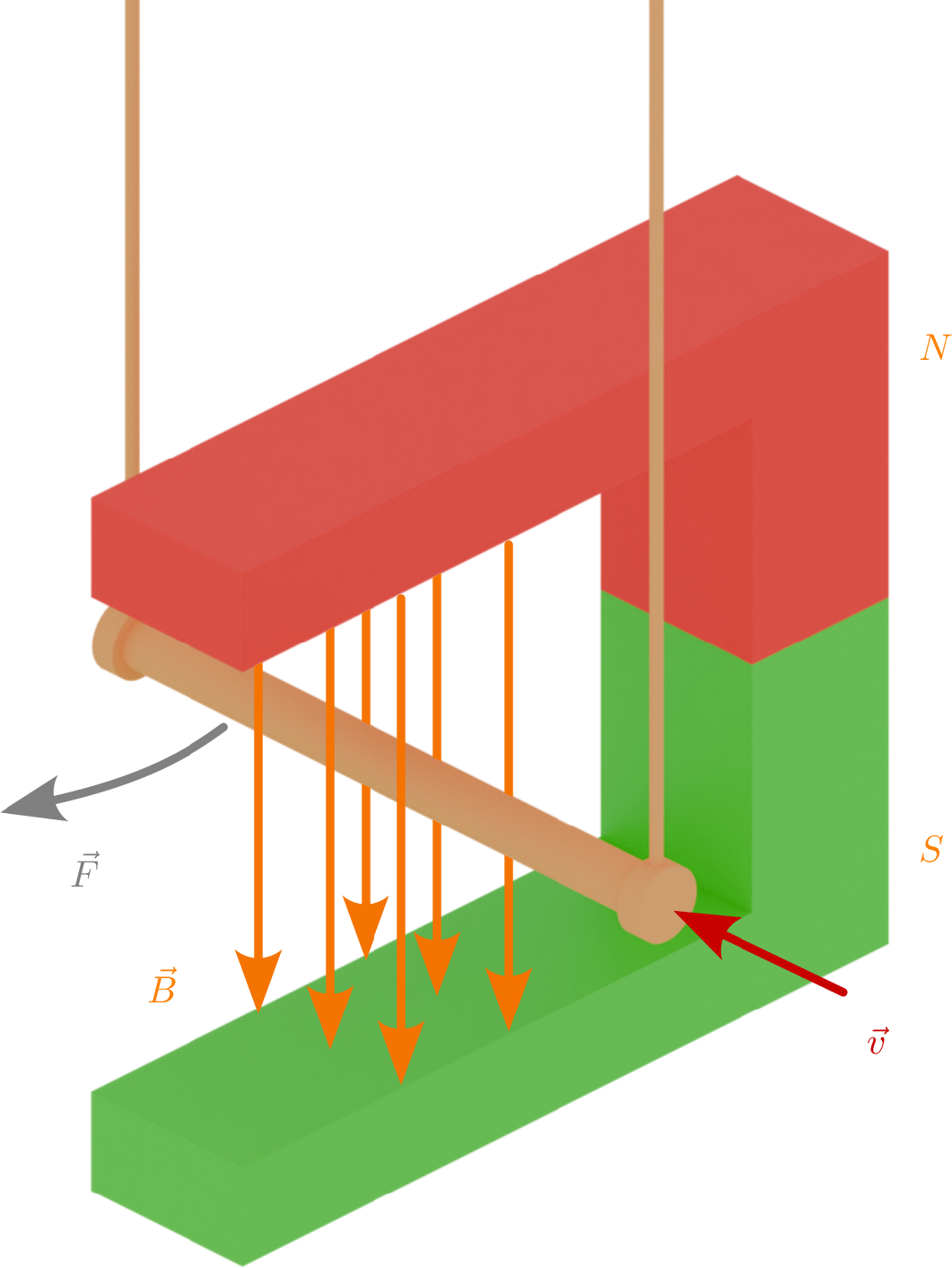
Abbildung zur Veranschaulichung der Lorentzkraft. Sie zeigt einen C-förmigen Permanentmagnet, der in rot (oberer Teil) und grün (unterer Teil) eingefärbt ist. In der Mitte befindet ein Draht innerhalb des Magnetfeldes des Magneten. Der Draht ist freischwingend an zwei Zuleitungen aufgehängt. Die Geschwindigkeit V beschreibt den Stromfluss durch den Leiter.

Bei der skalaren Berechnung entfallen die Vektoren, stattdessen wird der Winkel sin \(\alpha \) im Bezug auf die Geschwindigkeit \(v\) und das Magnetfeld \(B\) in die Rechnung einbezogen. Dabei gilt, dass die Lorentzkraft sowohl zu der Flussdichte, als auch auf der Geschwindigkeit der Ladung senkrecht steht. Der Betrag der Kraft ergibt sich bei geraden Leitern und konstantem Magnetfeld zu: \begin {align} F &= q \cdot v \cdot B \cdot \sin {\alpha }\\ F &=I\cdot \ell \cdot N \cdot B\cdot \sin {\alpha }\label {GlLorentzkraft} \end {align}

Die Gleichung ?? illustriert die skalare Berechung in einem stromdurchflossenen Leiter. \(\ell \) ist die wirksame Leiterlänge mit der Anzahl von \(N\) parallelen Leitern, die mit dem Strom \(I\) durchflossen werden. \(\alpha \) ist der Winkel zwischen dem Leiter und der Richtung der magnetischen Flussdichte \(\vec {B}\). Stehen Leiter und Magnetfeld senkrecht zueinander, entfällt \(\sin {\alpha }\).

Merke: Lorentzkraft

Die Lorentzkraft beschreibt die Kraft, die auf eine bewegte Ladung in einem Magnetfeld wirkt. Fließt die Ladung durch einen Leiter, so wirkt die Lorentzkraft senkrecht sowohl zum Stromfluss als auch zur magnetischen Flussdichte.

Zur Veranschaulichung des Prinzips eines Elektromotors wird eine stromdurchflossene Leiterschleife, die beweglich auf einem drehbar gelagerten Rotor befestigt ist, im Feld eines Permanentmagneten betrachtet:

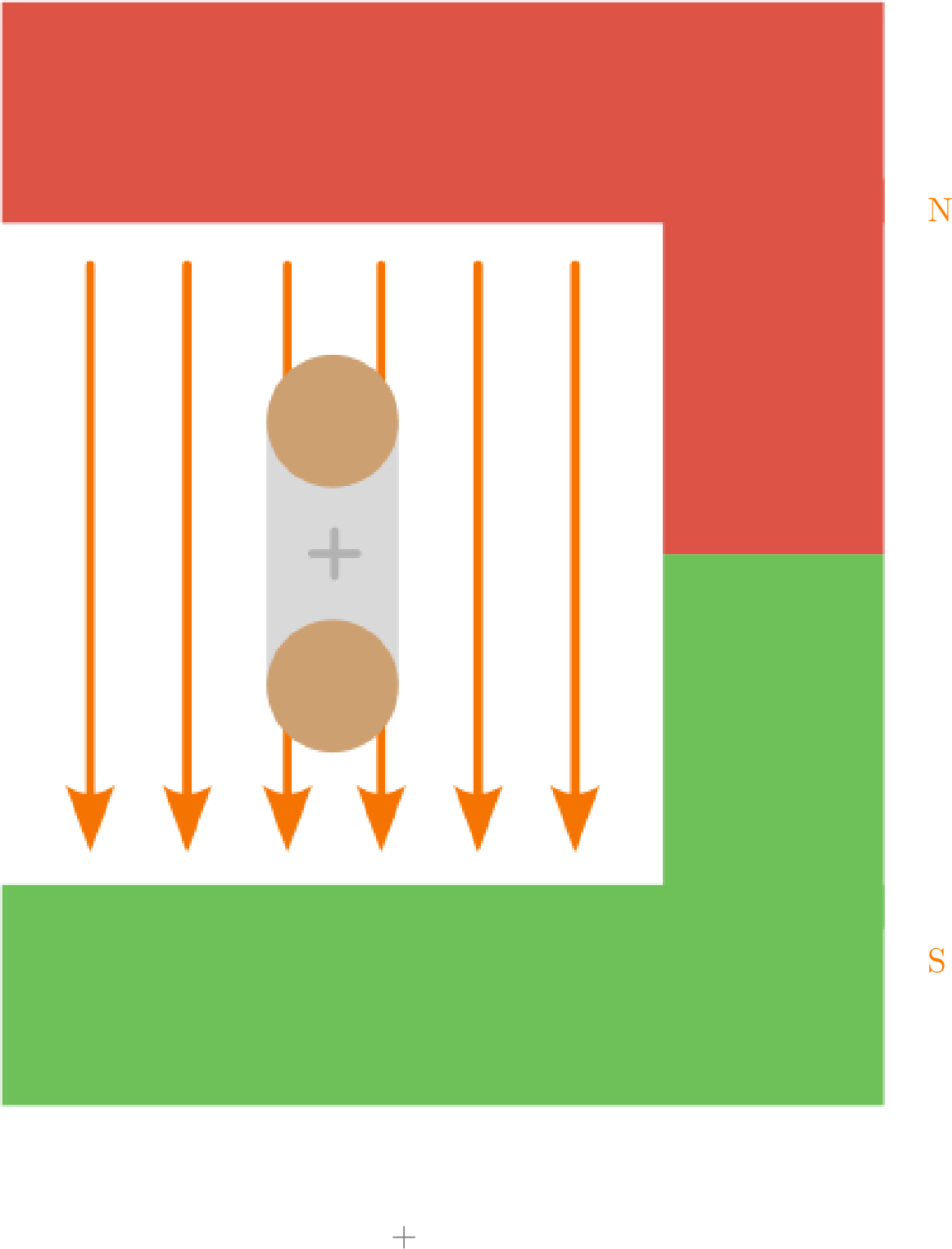
Ein C-förmiger Permanentmagnet ist zu sehen, dessen Magnetfeld vom N-Pol zum S-Pol (von oben nach unten) verweist. Eine Leiterschleife, die sich innerhalb des Magnetfeldes befindet, ist transparent abgebildet und wird ignoriert, da sie nicht stromdurchflossen ist.

  • Eine Leiterschleife befindet sich auf einem drehbaren Element, dem Rotor, im Magnetfeld eines Hufeisenmagneten.
  • Der Leiter ist hier noch nicht stromdurchflossen, sodass das Feld des Permanentmagneten einzeln betrachtet werden kann.
  • Die Magnetfeldlinien verlaufen außerhalb des Permanentmagneten vom Nord- zum Südpol.

Der C-förmige Permanentmagnet ist transparent abgebildet und wird nun ignoriert. Um die nun stromdurchflossene Leiterschleife entsteht ein magnetisches Feld in Abhängikeit der Flussrichtung.

  • Nun wird die Leiterschleife stromdurchflossen betrachtet, ohne das Feld des Permanentmagneten zu berücksichtigen.
  • Um die stromdurchflossene Leiterschleife entsteht ein magnetisches Feld in Abhängikeit der Flussrichtung des Stroms (Rechte-Hand-Regel).

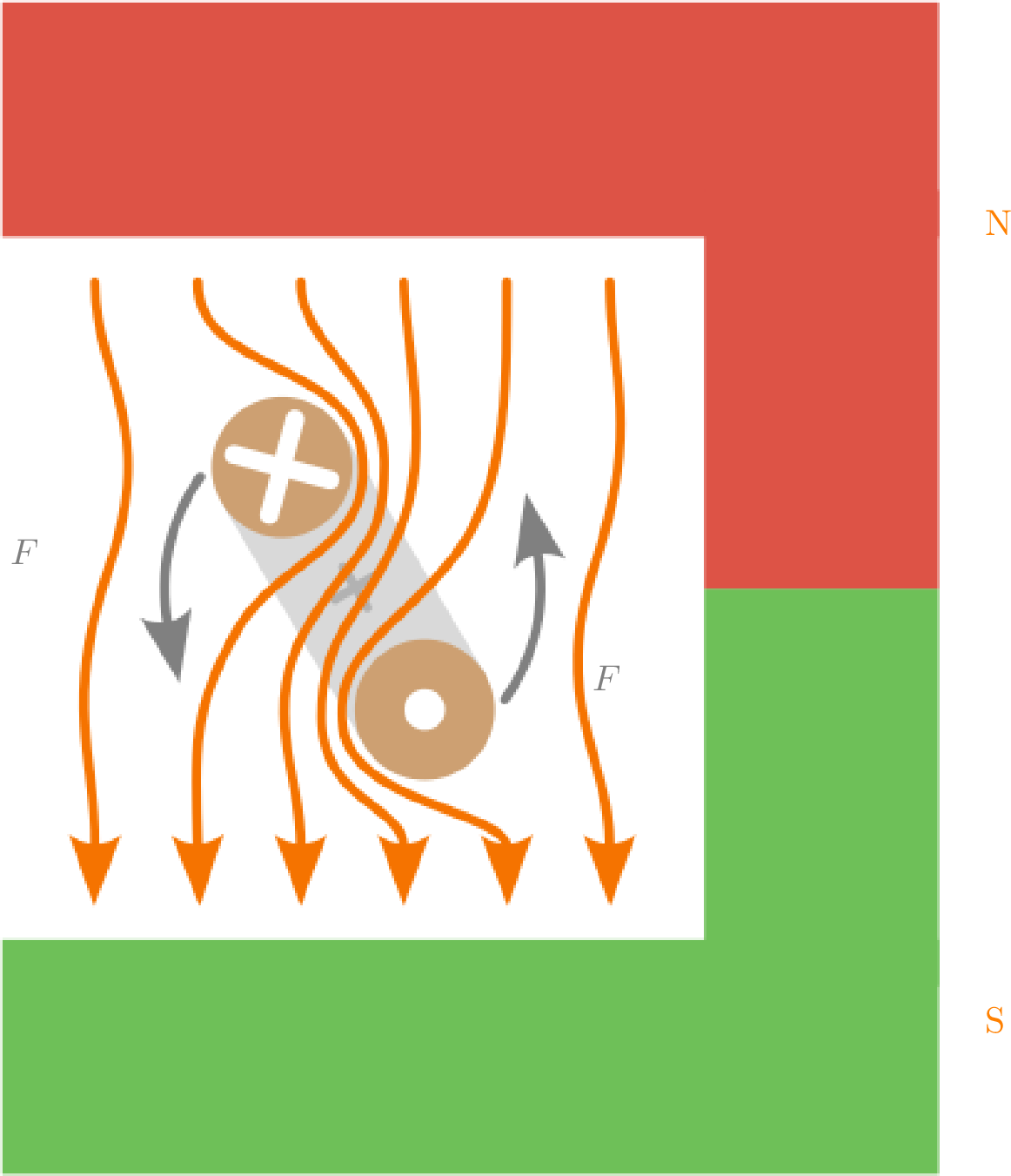
Das Magnetfeld des C-förmigen Permanentmagneten und das Magnetfeld der stromdurchflossenen Leiterschleife werden zusammen betrachtet. Das Magnetfeld der Leiterschleife lenkt das Magnetfeld des Permanentmagneten in deren Zusammenspiel ab, sodass eine Kraft entsteht, die entgegen des Uhrzeigersinns wirkt. Dadurch dreht sich die Leiterschleife entsprechend gegen den Uhrzeigersinn.

  • Das Feld des Permanentmagneten und das magnetische Feld der stromdurchflossenen Leiterschleife werden nun zusammen betrachtet.
  • Die Lorentzkraft, die je Leiter senkrecht zum Leiter und dem Magnetfeld steht, wirkt auf die Leiterschleife.
  • Die Leiterschleife beginnt sich aufgrund der Lorentzkraft zu drehen.

Wird der Stromfluss in der Leiterschleife umgekehrt, kehrt sich die Drehrichtung der Leiterschleife innerhalb des Magnetfeldes des Permanentmagneten um.

  • Hier wird die Flussrichtung des stromdurchflossen Leiters umgekehrt.
  • Entsprechend kehrt sich auch die Polung der stromdurchflossenen Leiterschleife und damit die Drehrichtung der Leiterschleife um (Drei-Finger-Regel).

Beispiel 1: Lorentzkraft

Ein Gleichstrommotor hat im Luftspalt eine magnetische Flussdichte von \(B=0,8\,\mathrm {T}\). Unter den Polen befinden sich insgesamt \(N=400\) Wicklungen, die mit einem Strom von \(I=10\,\mathrm {A}\) durchflossen werden. Die wirksame Leiterlänge ist \(\ell =150\,\mathrm {mm}\).

Berechnen Sie die Kraft \(F\) am Umfang des Ankers. \begin {align*} F & =B\cdot I\cdot \ell \cdot N \\ & =0,8\,\tfrac {\mathrm {Vs}}{\mathrm {m}^2}\cdot 10\,\mathrm {A}\cdot 0,15\,\mathrm {m}\cdot 400 \\ & =480\,\frac {\mathrm {kg}\cdot \mathrm {m}^2\cdot \mathrm {s}\cdot \mathrm {A}\cdot \mathrm {m}}{\mathrm {s}^3\cdot \mathrm {A}\cdot \mathrm {m}^2} = 480\,\mathrm {N} \end {align*}

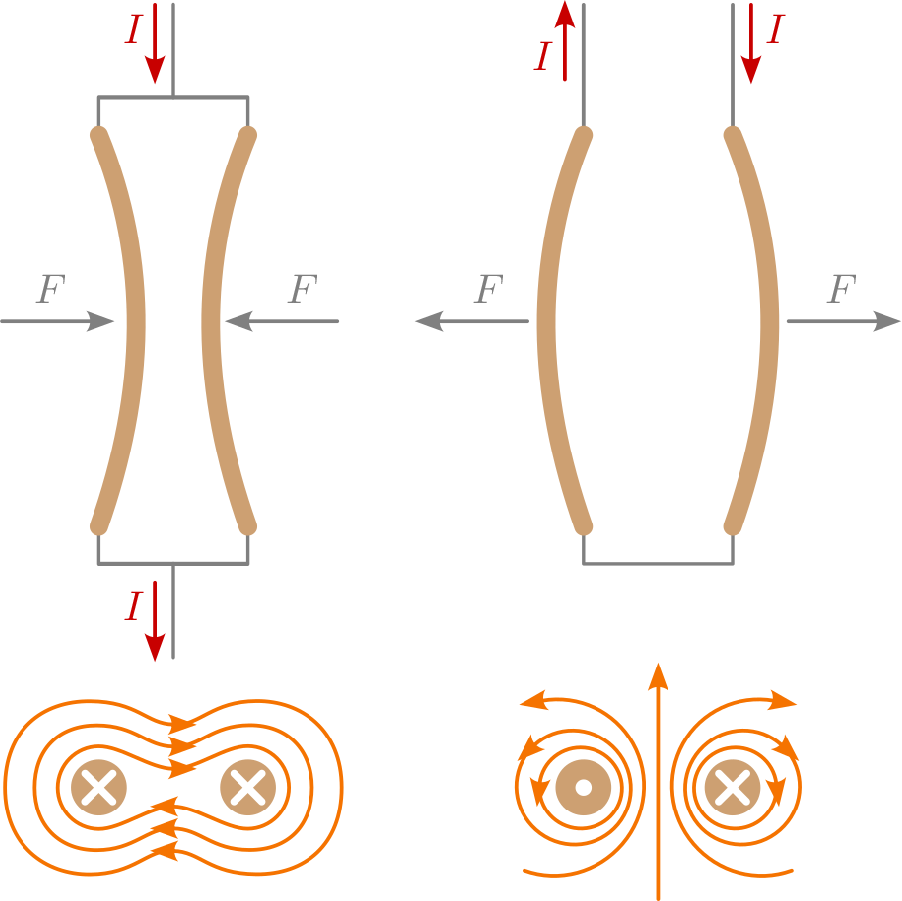
Zwei parallele Leiter, die von Strom durchflossen werden, üben ebenfalls eine Lorentzkraft aufeinander aus, da jeder stromdurchflossene Leiter um sich herum ein Magnetfeld aufbaut (siehe Abbildung 2). Ist die Stromrichtung in beiden Leitern gleich, entsteht eine Anziehungskraft, bei umgekehrter Stromrichtung wirkt die Kraft abstoßend.

Die Abbildung zeigt zwei unterschiedliche Versuchsaufbauten: Auf der linken Seite sind zwei parallel von oben nach unten verlaufende Drähte abgebildet, die beide in der gleichen Richtung stromdurchflossen werden. Daurch entsteht ein Magnetfeld um die Drähte, das eine Krat verursacht, die die Drähte konkav zusammenzieht. Auf der rechten Seite ist ein fast identischer Versuchsaufbau abgebildet, jedoch werden hier die Drähte engegengesetzt stromdurchlossen. Dies erzeugt ein Magnetfeld um die Drähte, das diese voneinander abstößt und somit konvex verformt.

Abbildung 2: Lorentzkraft zwischen zwei parallelen Leitern. Ist die Flussrichtung des Stroms gleich, ziehen sie sich an. Bei gegensätzlicher Flussrichtung stoßen sich die Leiter ab.

Für den theoretischen Spezialfall zweier geraden, parallelen, dünnen und unendlich langen Drähte gilt das Verhältnis:

\begin {equation} F_{1,2} = \frac {\ell \cdot \mu _0\cdot I_1\cdot I_2}{2\cdot \pi \cdot r} \end {equation}

Da in der Praxis diese speziellen Voraussetzungen nicht zutreffen, dient die Formel lediglich als Näherung an reale Fälle, um die Krafteinwirkung der Lorentzkraft abschätzen zu können.

Expand
×

...