Induktivität
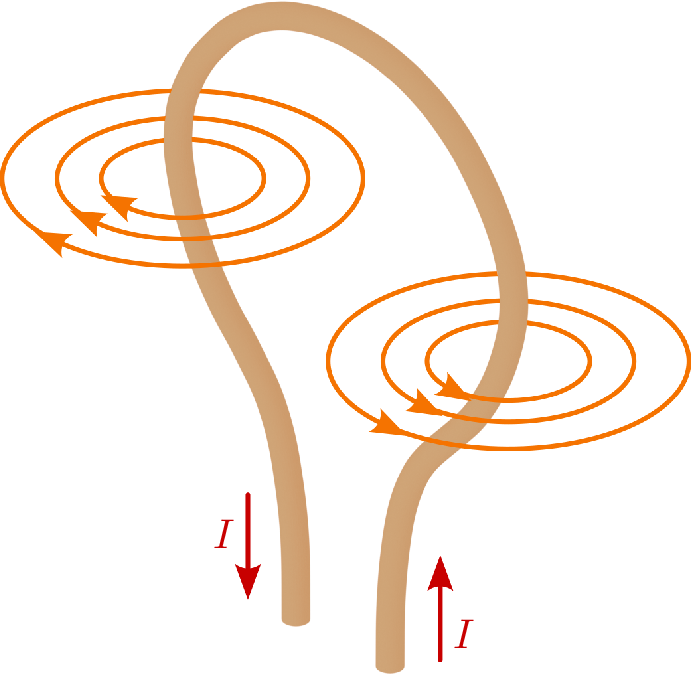
Die Induktivität beschreibt die Fähigkeit, elektrische Energie in einem magnetischen Feld zu speichern. Bauelemente, die diese Fähigkeit besitzen, werden Spule (Abbildung 1), Drossel oder auch Induktivität genannt.
Die Funktionsweise einer Induktivität beruht auf dem elektromagnetischen Feld, das durch den Stromfluss erzeugt wird. Dieses elektromagnetische Feld induziert einen Strom in benachbarten Leiterspulen des Bauelements. Durch diesen Effekt kann elektrische Energie vorübergehend in einem magnetischen Feld gespeichert werden. Zum besseren Verständnis wird im Folgenden die Funktion der Induktivität schrittweise erklärt.
Eine Leiterschleife wird von Strom durchflossen. Dieser Strom erzeugt ein Magnetfeld, dessen Stärke proportional zur Stromstärke ist – je stärker der Strom, desto stärker das Magnetfeld. Wird die Stromstärke kontinuierlich geändert, erzeugt dies ebenso eine Änderung des Magnetfeldes, welche wiederum (wie in Kapitel ?? beschrieben) eine Spannung in benachbarten Leiterschleifen induziert. Diese induzierte Spannung wirkt gemäß der Lenzschen Regel der Änderung des Stroms entgegen. Folglich wirkt beim Einschalten der Stromquelle an der Spule die induzierte Spannung dem Stromfluss entgegen, sodass der Strom erst allmählich ansteigt. Beim Ausschalten der Spule bewirkt die induzierte Spannung, dass der Strom noch eine Zeit lang nachfließt. Diese Gegebenheit, auch Selbstinduktion genannt, ermöglicht eine magnetische Speicherung. Die Induktivität gibt folglich an, wie stark sich ein elektrisches Bauteil selbstinduziert. Die Höhe der Induktität \(L\) hängt ab von der Anzahl der Windung \(N\), der Permeabilität des Spulenkerns \(\mu _r\), der Querschnittsfläche des Kerns und der geometrischen Form des Bauteils. Für Induktivitäten gilt im Allgemeinen, dass das magnetische Feld sich proportional zum Wert des Stroms verhält.
Rechnerisch lässt sich die Induktivität \(L\) mit der Einheit Henry (H) auf zwei unterschiedliche Weisen ermitteln. Zum einen kann sie mittels der Relation des entstehenden Magnetfelds \(N \cdot \varPhi \) zu dem verursachenden Strom \(I\) (wie in Gleichung 1) berechnet werden.
\begin {equation} L = \frac {N \cdot \varPhi }{I} \label {InduktivitaetFormel} \qquad [\mathrm {H}] \end {equation}
Zum anderen kann die Induktivität bei einfachen geometrischen Strukturen, wie zum Beispiel zylindrische, rechteckige oder Ringkerspulen, über die Relation der Windungen \(N^2\) zu dem magnetischen Widerstand \( R_{\mathrm {m}} \) bestimmt werden (Gleichung 2).
\begin {equation} L=\frac {N^2}{R_{\mathrm {m}}} \label {InduktivitaetFormel2} \qquad [\mathrm {H}] \end {equation}
Merke: Induktivität
Die Induktivität \(L\) beschreibt ein Bauelement, das in der Lage ist, elektrische Energie in einem magnetischen Feld zu speichern.
Die Berechnung der Spannung einer Induktivität lässt sich von der Berechnung der Spannung einer Induktion ableiten (Gleichung ??).
\begin {equation} u_{\mathrm {i}} = -N\cdot \frac {\mathrm {d}\varPhi }{\mathrm {d}t} \tag {\ref {GlInduktionsgesetz}} \end {equation}
Die Spannung einer Induktivität \(u\) ist eine zeitliche Änderung des Stromes \({\mathrm {d}i}/{\mathrm {d}t}\) multipliziert mit der Induktivität \(L\). Auch hier findet die Lenzsche Regel Anwendung, welche ein negatives Vorzeichen zur Folge hat.
\begin {equation} u =-L\cdot \frac {\mathrm {d}i}{\mathrm {d}t}\label {GLInduktivitaet2} \end {equation}
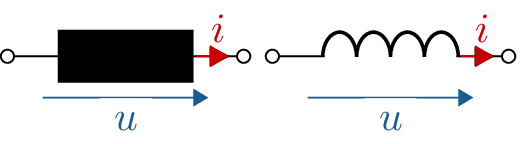
In Schaltplänen werden Induktivitäten mittels schwarz gefüllter Rechtecke, wie in der oberen der beiden Abbildungen 3 dargestellt. Seltener wird ein gewundener Leiter, wie in der unteren Abbildung 3 für die Darstellungen einer Induktivität genutzt.
Um die Induktivität einer Struktur zu bestimmen, gibt es zwei Möglichkeiten: Den Weg der Ermittlung über die Feldgrößen und den Weg über den magnetischen Widerstand.
Weg 1 über die Feldgrößen:
- 1.
- Annahme einer
Stromstärke \(I\) \(\rightarrow \) Durchflutung\(\Theta = N\cdot I\)
- 2.
- Feldstärke berechnen
\(H=\frac {\Theta }{\ell _{\mathrm {m}}}\)
- 3.
- Flussdichte berechnen
\(B=\mu _{\mathrm {r}}\cdot \mu _0\cdot H\)
- 4.
- Magnetischen Fluss bestimmen
\(\varPhi = \iint _A \vec {B}\cdot \mathrm {d}\vec {A}\)
- 5.
- Induktivität
\(L=\frac {N\cdot \varPhi }{I}\)
Widerstand:
- 1.
- Magnetkreis in Teilabschnitte
zerlegen und magnetischen
Widerstand \(R_{\mathrm {m}}\) berechnen\(R_{\mathrm {m}}=\frac {\ell _{\mathrm {m}}}{\mu _{\mathrm {r}}\cdot \mu _0\cdot A}\)
- 2.
- Gesamtwiderstand berechnen
(bei Reihenstruktur)\(R_{m,\mathrm {ges}} = \sum R_{\mathrm {m}}\)
- 3.
- Induktivität
\(L=\frac {N^2}{R_{m,\mathrm {ges}}}\)
Beispiel 1: Induktivität
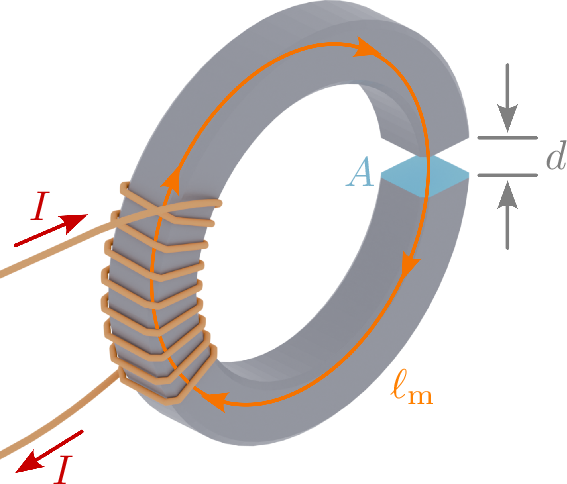
Bei einer Ringkernspule mit Luftspalt soll der Einfluss des Luftspaltes \(d\) auf die Induktivität \(L\) untersucht werden. Die Spule hat \(N=100\) Windungen. Die relative Permeabilität beträgt \(\mu _{\mathrm {r}}=2000\). Die mittlere Eisenkernlänge beträgt \(\ell _{\mathrm {m}}=5\,\mathrm {cm}\). Die Querschnittsfläche beträgt \(A=1\,\mathrm {cm}^2\).
-
Der Luftspalt ist vorerst nicht vorhanden: \(d=0\). Wie groß ist die Induktivität \(L\)?
\begin {align*} R_{\mathrm {m}} & = \frac {\ell _{\mathrm {m}}}{\mu _{\mathrm {r}}\cdot \mu _0\cdot A} \\ L & = \frac {N^2}{R_{m}} \\ & = \frac {100^2\cdot 2000\cdot 1,256\cdot 10^{-6}\,\frac {\mathrm {Vs}}{\mathrm {Am}}\cdot 1\cdot 10^{-4}\,\mathrm {m}^2}{0,05\,\mathrm {m}} \\ L & = 0,05\,\frac {\mathrm {Vs}}{\mathrm {A}} = 50\,\mathrm {mH} \end {align*}
- Der Luftspalt beträgt nun \(d=1\,\mathrm {mm}\). Wie groß ist die Induktivität? \begin {align*} R_{\mathrm {m}} & = R_{m,\mathrm {Fe}} + R_{m,\mathrm {L}} \\ L & = \frac {\ell _{\mathrm {m}} - d}{\mu _{\mathrm {r}}\cdot \mu _0\cdot A} + \frac {d}{\mu _0\cdot A} \\ L & = \frac {0,05\,\mathrm {m} - 0,001\,\mathrm {m}}{2000\cdot 1,256\cdot 10^{-6}\,\frac {\mathrm {Vs}}{\mathrm {Am}}\cdot 1\cdot 10^{-4}\,\mathrm {m}^2} + \frac {0,001\,\mathrm {m}}{ 1,256\cdot 10^{-6}\,\frac {\mathrm {Vs}}{\mathrm {Am}} \cdot 1\cdot 10^{-4}\,\mathrm {m}^2} \\ L & = 1,226\,\mathrm {mH} \end {align*}