Energie im magnetischen Feld

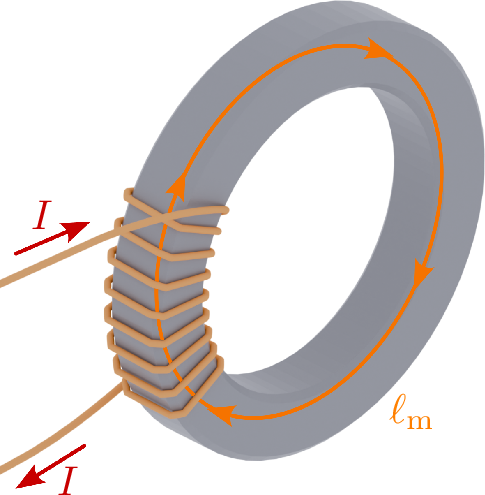
Um die Energie, die in einer Spule gespeichert ist, zu berechnen, wird die in der Abbildung 1 illustrierte Ringkernspule an eine Gleichspannungsquelle angeschlossen. Zum Zeitpunkt \(t = 0\) wird die Spannungsquelle eingeschaltet. Die Spannung an der Spule ist dadurch zu jedem Zeitpunkt \(t > 0\) gleich der Quellenspannung \(U\). Der durch die Spule geleitene Strom wird nach Gleichung ?? linear ansteigen. Die dadurch zugeführte Energie erzeugt eine Flussdichte im Spulenkern. Um die Energie zu berechnen, die der Spule zugeführt wird, kann bekannte Gleichung der elektrischen Leistung ?? umgeformt werden und anschließend die Spannung durch Gleichung ?? ersetzt werden. Als Ergebnis dieser Umformung erhält die Änderung der magnetischen Energie \(\mathrm {d}W_{\mathrm {L}}\), welche aus der Multiplikation von Induktivität \(L\), dem Strom durch die Induktität \(i_{\mathrm {L}}\) und der Änderungsrate des Stroms durch die Induktität \(\mathrm {d}i_{\mathrm {L}}\) errechnet (siehe Gleichung ??).

\begin {align} p &= \frac {\mathrm {d}W}{\mathrm {d}t} = u\cdot i \label {GlArbeit}\\ u &= L\cdot \frac {\mathrm {d}i}{\mathrm {d}t} \tag {\ref {GLInduktivitaet2}}\\ \mathrm {d}W_{\mathrm {m}}&=u_{\mathrm {L}}\cdot i_{\mathrm {L}} \cdot \mathrm {d}t = L\cdot \frac {\mathrm {d}i}{\mathrm {d}t}\cdot i_{\mathrm {L}}\cdot \mathrm {d}t = L\cdot i_{\mathrm {L}} \cdot \mathrm {d}i_{\mathrm {L}} \label {GlÄnderungmagnetischeEnergie} \end {align}

Die Gesamtenergie ist das Integral über \(\mathrm {d}W_{\mathrm {m}}\) vom Anfangswert \(i_{\mathrm {L}}=0\) bis zum statischen Endwert \(i_{\mathrm {L}} = I\). Unter der Voraussetzung einer konstanten Induktivität \(L\) gilt dann:

\begin {equation} W_m = L \cdot \int _0^{I_L} i_L \cdot \mathrm {d}i_L = \frac {1}{2} \cdot L \cdot I^2 = \frac {1}{2} \cdot N \cdot \varPhi \cdot I \end {equation}

Die magnetische Energie kann auch aus den Feldgrößen durch Integration mit der magnetischen Flussdichte errechnet werden: \begin {equation} W_{\mathrm {m}} = \ell _{\mathrm {m}}\cdot A\cdot \int \limits _0^{B_L} H\mathrm {d}B = \ell _{\mathrm {m}}\cdot A \cdot \frac {B_{\mathrm {L}}^2}{2\cdot \mu _{\mathrm {r}}\cdot \mu _0} \end {equation} Bei einem Elektromagneten hat die Energiedichte im Luftspalt (also die Energie pro Volumen des Luftspalts) eine besondere Bedeutung: Sie steht für die „Kraft des Elektromagneten“. Die maximale Kraftwirkung befindet sich genau am Übergang vom Luftspalt zum Eisenkern – entspricht also einem theoretisch unendlich schmalen Luftspalt. Da der Luftspalt, wie der Name schon sagt, meistens mit Luft gefüllt ist, ist im Normalfall \(\mu _{\mathrm {r}} = 1\) und kann weggelassen werden.

\begin {equation} \frac {W_{\mathrm {m}}}{V} = \frac {B_{\mathrm {L}}^2}{2\cdot \mu _0} = \frac {F}{A} \end {equation}