Skin-Effekt

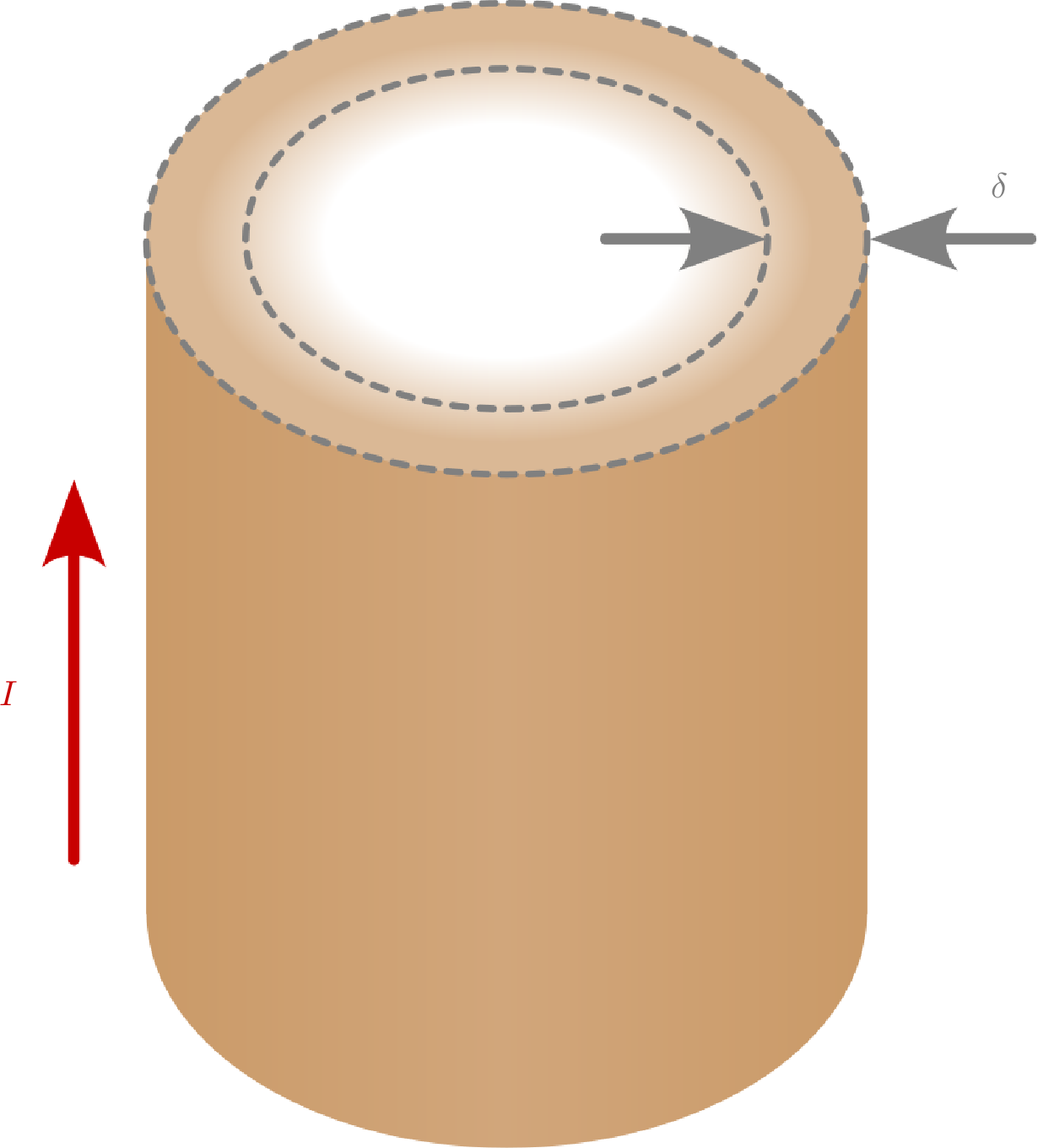
Der Skin-Effekt beschreibt das Phänomen, dass sich die Stromübertragung eines mit Wechselstrom durchflossenen Leiters vom Kern zu dessen äußerem Rand verlagert. Dieser Effekt basiert auf dem Prinzip der Induktion und tritt daher ausschließlich bei der Wechselstromübertragung auf.

Der Wechselstrom verursacht stetig sich ändernde magnetische Felder. Diese magnetischen Felder wirken gemäß der Lenz´schen Regel der Ursache entgegen und sind im Leiterinneren stärker ausgeprägt als in den Randbereichen. Es kommt zu einer elekrischen Feldschwächung im Leiterinneren, sodass die Stromübertragung an den Rand des Leiters stattfindet. Wie weit der Wechselstrom in den Leiter eindringt, wird mit der Skin-Tiefe \(\delta \) (Delta) beschrieben. Dabei gilt, dass mit steigender Frequenz die Feldschwächung im Kern zunimmt. Die Tabelle 1 veranschaulicht die Auswirkungen des Skin-Effekts am Beispiel einer Kupferleitung. Während bei einer Frequenz von 5 Hz die Skin-Tiefe 29,7 mm beträgt, so schrumpft diese bei einer Frequenz von 500 Hz auf 2,97 mm.

PIC

Abbildung 1: Skin-Effekt. Die Skin-Tiefe \(\delta \) beschreibt, wie Tief der Wechselstrom in den Leiter eindringt.

Tabelle 1: Exemplarische Übersicht zur Skin-Tiefe. Eindringtiefe in eine Kupferleitung in Abhängigkeit der Frequenz:
Frequenz Skin-Tiefe \(\delta _{Cu}\)
\(5\,\mathrm {Hz}\) \(29,7\,\mathrm {mm}\)
\(50\,\mathrm {Hz}\) \(9,38\,\mathrm {mm}\)
\(500\,\mathrm {Hz}\) \(2,97\,\mathrm {mm}\)
\(500\,\mathrm {kHz}\) \(93,8\,\mu \mathrm {m}\)

Zur Berechnung des Skin-Effekts wird die Skin-Tiefe \(\delta \) ermittelt. Die Skin-Tiefe wird durch die Wurzel des spezifischen Widerstands \(\rho _\mathrm {R}\) geteilt durch das Produkt der Frequenz \(f\), der Zahl Pi \(\pi \) und der materialabhängigen magnetischen Permeabilität \(\mu \) errechnet (siehe Gleichung 1).

\begin {equation} \delta = \sqrt {\frac {\rho _\mathrm {R}}{\pi \cdot \mu \cdot f}} \label {GlSkinTiefe} \end {equation}

Merke: Skin-Effekt

Der Skin-Effekt verursacht die Verdrängung von Wechselstrom an den Rand des Leiters.

Beispiel 1: Skin-Tiefe

Ein Kupferleiter wird mit Strom der Frequenz \(f = 50 \, \mathrm {Hz}\) durchflossen. Für den Leiter sind folgende Werte gegeben:

  • Absolute magnetische Permeabilität: \(\mu = 4\pi \cdot 10^{-7} \, \frac {\mathrm {Vs}}{\mathrm {Am}}\)
  • Spezifischer Widerstand: \(\rho _{R} = 0,01721 \, \frac {\Omega \cdot \mathrm {mm}^2}{\mathrm {m}}\)

Berechnen Sie die Skin-Tiefe \(\delta \) des Leiters.

\begin {align*} \onslide <2-> {\delta &= \sqrt {\frac {\rho _\mathrm {R}}{\pi \cdot \mu \cdot f}}} \\ \onslide <3-> {\delta &= \sqrt {\frac {0,01721 \, \frac {\Omega \cdot \mathrm {mm}^2}{\mathrm {m}}}{\pi \cdot 4\pi \cdot 10^{-7} \, \frac {\mathrm {Vs}}{\mathrm {Am}} \cdot 50 \, \mathrm {Hz}}}} \\ \onslide <4-> {\delta &\approx 9,34 \, \mathrm {mm}} \end {align*}

Expand
×

...