Hall-Effekt

Der Hall-Effekt beschreibt das Auftreten einer elektrischen Spannung innerhalb eines stromdurchflossenen Leiters aufgrund der Ladungsverschiebung durch ein magnetisches Feld.

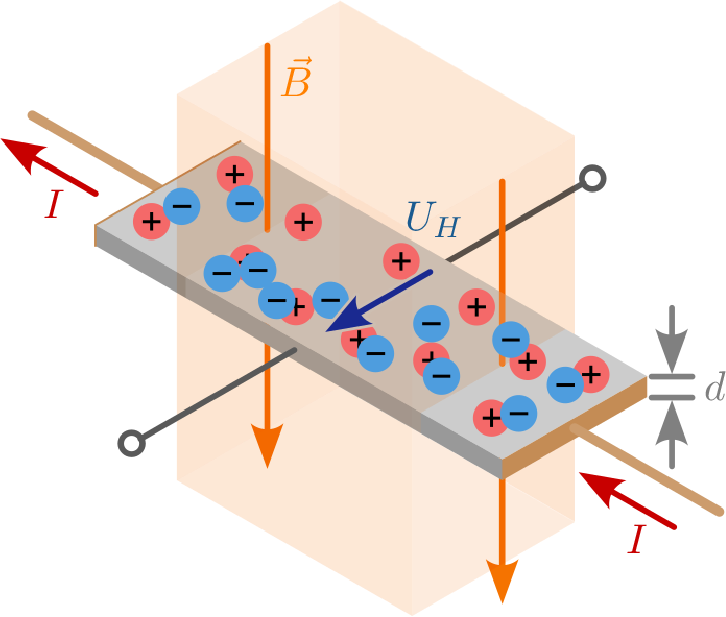
In der Abbildung 1 wird der Leiter, ähnlich wie im Versuchsaufbau zur Lorentzkraft, von einem magnetischen Feld durchflossen. Der Leiter ist hier allerdings plattenförmig dargestellt, so dass sich die Ladungsträger über die gesamte Leiterfläche bewegen können. Wird nun der Leiter mit Strom durchflossen, wirkt auf die bewegten Ladungen die Lorentzkraft. Diese verursacht gemäß der Rechten-Hand-Regel eine senkrechte Ablenkung der Ladungsträger im Leiter zum Rand. Durch die Ladungsverschiebung entsteht im Leiter ein elektrisches Feld, welches der Lorentzkraft entgegengerichtet ist. An den Rändern des Leiters kann die aus der Ladungsverschiebung resultierende Spannungsdifferenz gemessen werden. Sie wird als Hall-Spannung \(U_{\mathrm {H}}\) bezeichnet.

PIC

Abbildung 1: Versuchsaufbau zum Hall-Effekt. Die durch das Magnetfeld entstehende Lorentzkraft lenkt die bewegten Ladungsträger senkrecht an den Rand ab. Diese Ladungsverschiebung erzeugt eine elektrisch messbare Spannung – die Hall-Spannung.

Zur Ermittlung der Hall-Spannung \(U_\mathrm {H}\) wird die Hall-Konstante \(A_\mathrm {H}\) benötigt. Die Hall-Konstante \(A_\mathrm {H}\) ist eine Materialgröße, die Aufschluss über die Ladungsträgerdichte und damit über die Leitfähigkeit des Materials gibt.

Die Hall-Spannung kann (wie in Gleichung 1 dargestellt) durch die Multiplikation der Hall-Konstante \(A_{\mathrm {H}}\) mit dem Produkt der Stromstärke \(I\) und der magnetischen Flussdichte \(B\) dividiert durch die Dicke des stromdurchflossenen Plättchens \(d\) errechnet werden.

\begin {equation} U_{\mathrm {H}} = A_{\mathrm {H}} \cdot \frac {I \cdot B}{d} \label {GlHallSpannung} \end {equation}

Merke: Hall-Effekt

Die Hall-Spannung \(U_{\mathrm {H}}\) beschreibt das Auftreten einer elektrischen Spannung innerhalb des stromdurchflossenen Leiters senkrecht zum Stromfluss aufgrund eines einwirkenden Magnetfeldes.

Beispiel 1: Hall-Spannung

Ein mit der Stromstärke \(I = 2\,\mathrm {A}\) stromdurchflossenes Metallplättchen mit der Dicke \(d = 1\,\mathrm {cm}\) befindet sich in einem Magnetfeld mit der Flussdichte \(B = 0,5\,\mathrm {T}\). Die Hall-Konstante des Materials beträgt \(A_{\mathrm {H}} = 3,2 \cdot 10^{-3} \, \frac {\mathrm {m}^3}{\mathrm {C}}\). Berechnen Sie die Hall-Spannung.

\begin {align*} \onslide <2->{U_{\mathrm {H}} & = A_{\mathrm {H}} \cdot \frac {I \cdot B}{d}}\\ \onslide <3->{U_{\mathrm {H}} & = 3,2 \cdot 10^{-3} \, \tfrac {\mathrm {m}^3}{\mathrm {C}} \cdot \frac {2 \, \mathrm {A} \cdot 0,5 \, \mathrm {T}}{0,01 \, \mathrm {m}}}\\ \onslide <4->{U_{\mathrm {H}} & = 0,32 \, \mathrm {V}} \end {align*}

Expand
×

...