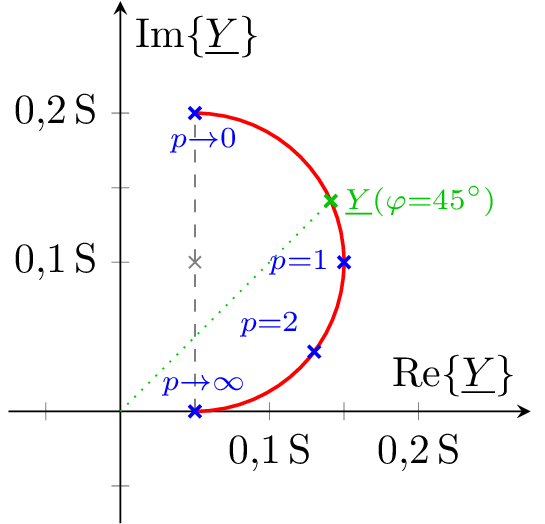Im Modul 8
Aufgaben
WiederholungDie Ausgangsspannung eines RC-Tiefpasses soll bei der Frequenz \(f=1\,\mathrm {kHz}\) nur noch \(10\,\%\) der Eingangspannung betragen. Wie groß ist die Grenzfrequenz zu wählen?
\begin {align*} \underline {F}(\mathrm {j}\omega )&=\frac {\underline {U}_a}{\underline {U}_e} = \frac {\frac {1}{j\omega C}}{\frac {1}{j\omega C} + R} = \frac {1}{1 + j\omega RC}\\ A(\omega )&=\frac {U_a}{U_e} = \frac {1}{\sqrt {1+(\omega RC)^2}}\\ A(\omega _g)&=\frac {1}{\sqrt {1+(\omega _g RC)^2}} \overset {!}{=} \frac {1}{\sqrt {2}} \Rightarrow \omega _g = \frac {1}{RC} \\ A(\omega )&\overset {!}{=} 0,1 \Rightarrow \sqrt {1+(\omega RC)^2} \overset {!}{=} 10\\ \Leftrightarrow 1 + (\omega RC)^2 &= 100 \Leftrightarrow (\omega RC)^2 = 99 \Rightarrow \omega _g = \frac {\omega }{\sqrt {99}}\\ \Rightarrow f_g &= \frac {f}{\sqrt {99}} = \frac {1\,\mathrm {kHz}}{\sqrt {99}} = 100,5\,\mathrm {Hz} \end {align*}
Wie groß ist die Phasenverschiebung \(\varphi \) bei einem RC-Hochpass 1. Ordnung, wenn die Sperrdämpfung (Verhältnis von Ausgangs- zu Eingangsspannung) \(-6\,\mathrm {dB}\) beträgt?
\begin {align*} -6\,\mathrm {dB} &= 20\cdot \lg \left (\frac {U_a}{U_e}\right )\,\mathrm {dB} \\ \Rightarrow -0,3 &= \lg \left (\frac {U_a}{U_e}\right )\\ \Rightarrow \frac {U_a}{U_e} &= 10^{-0,3} = 0,501\\ \frac {\underline {U}_a}{\underline {U}_e} &= \frac {R}{R+\frac {1}{j\omega C}} = \frac {1}{1-j\frac {1}{\omega CR}}\\ \frac {U_a}{U_e} &= \frac {1}{\sqrt {1+\frac {1}{(\omega CR)^2}}} \overset {!}{=} 0,501\\ \Leftrightarrow \sqrt {1 + \frac {1}{(\omega CR)^2}} &= \frac {1}{0,501}\\ \Leftrightarrow \frac {1}{(\omega CR)^2} &= 2,981 \Leftrightarrow \frac {1}{\omega CR} = \sqrt {2,981} = 1,727\\ \frac {\underline {U}_a}{\underline {U}_e} &= \frac {1+j\frac {1}{\omega CR}}{1+\frac {1}{(\omega CR)^2}}\\[0.75em] \varphi &= \arctan \left (\frac {1}{\omega CR}\right ) = \arctan \left (\sqrt {2,981}\right ) = 59,92^\circ \end {align*}
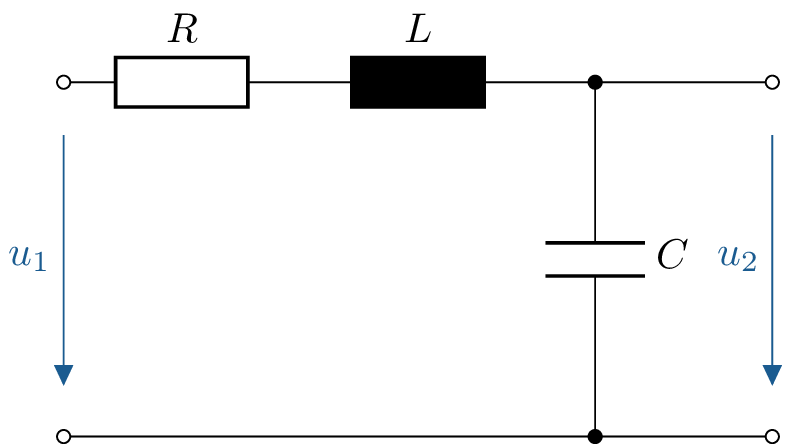
Gegeben ist unten dargestellte Schaltung mit \(L = 20\,\mathrm {mH}\), einem Widerstand \(R = 150\,\Omega \) und einem Kondensator mit
\(C = 1\,\mu \mathrm {F}\).
\begin {align*} \underline {Z} &= R + \mathrm {j}\omega L + \frac {1}{\mathrm {j} \omega C} = R + \mathrm {j}\cdot \left (\omega L + \frac {1}{\omega C}\right ) &&\Rightarrow \omega _0 L - \frac {1}{\omega _0 C} \overset {!}= 0 \\ \Rightarrow \omega _0 &= \frac {1}{\sqrt {LC}} = \frac {1}{\sqrt {20\,\mathrm {mH} \cdot 1\,\mu \mathrm {F}}} = 7071,07\,\mathrm {s}^{-1} &&\Rightarrow f_0 = \frac {\omega _0}{2\pi } = 1125,4\,\mathrm {Hz} \end {align*}
Da die Schaltung eine Reihenschaltung aus einem Widerstand, Kondensator und einer Spule ist, handelt es sich um eine Spannungsresonanz.
\begin {align*} \frac {\underline {U}_2}{\underline {U}_1} = \underline {F}(\mathrm {j}\omega ) &= \frac {\underline {Z}_{\mathrm {C}}}{\underline {Z}_{\mathrm {R}} + \underline {Z}_{\mathrm {L}} + \underline {Z}_{\mathrm {C}}} \\ &= \frac {\frac {1}{\mathrm {j}\omega C}}{R + \mathrm {j}\omega L + \frac {1}{\mathrm {j}\omega C}} &&\bigg | \cdot \frac {\mathrm {j}\omega C}{\mathrm {j}\omega C} \\ &= \frac {1}{\mathrm {j}\omega CR + \mathrm {j}^2 \omega ^2 LC + 1} \\ &= \frac {1}{1 - \omega ^2 LC + \mathrm {j} \omega R C} \end {align*}
\begin {align*} \left | \underline {F}(\mathrm {j}\omega ) \right | = A(\omega ) &= \frac {1}{\sqrt {(1-\omega ^2 LC)^2 + (\omega R C)^2 }} \end {align*}
Der Betrag des Frequenzganges ist in folger Abbildung dargestellt.
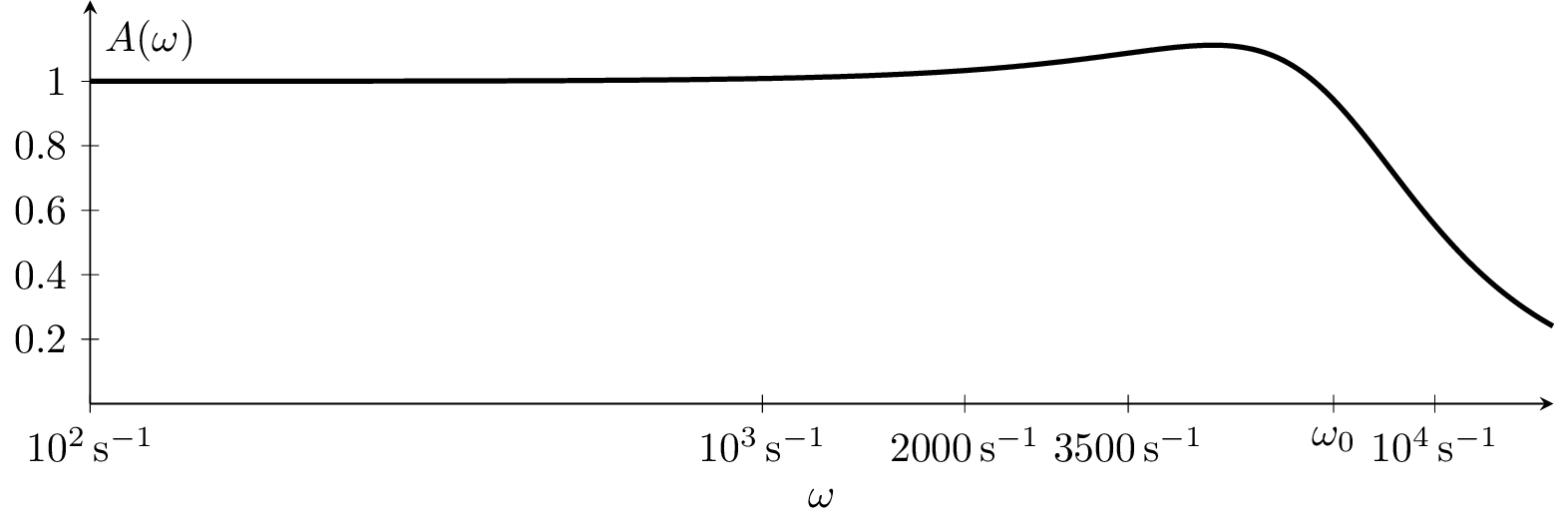
Die zugehörigen Werte sind:
| \(\omega \) | \(0\) | \(100\,\mathrm {s}^{-1}\) | \(2000\,\mathrm {s}^{-1}\) | \(3500\,\mathrm {s}^{-1}\) | \(\omega _0\) | \(10000\,\mathrm {s}^{-1}\) | \(\omega \to \infty \) |
| \(A(\omega )\) | \(1,000\) | \(1,009\) | \(1,033\) | \(1,087\) | \(0,943\) | \(0,555\) | \(0\) |
\begin {align*} \frac {U_2(\omega _0)}{U_1(\omega _0)} = Q_S &= \frac {X_k}{R} = \frac {\omega _0 L}{R} = \frac {1}{R}\cdot \sqrt {\frac {L}{C}}\\ &= \frac {1}{150\,\Omega }\cdot \sqrt {\frac {10\,\mathrm {mH}}{1\,\mu \mathrm {F}}}= 0,\overline {66} \end {align*}
Für \(L=10\,\mathrm {mH}\) ist \(Q_S < 1\), es kommt also zu keiner Spannungsüberhöhung im Resonanzfall.
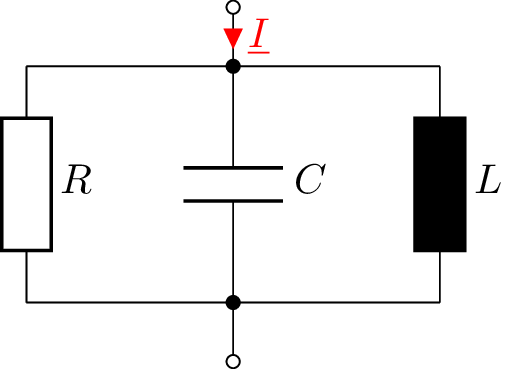
Die unten dargestellte Schaltung soll untersucht werden. Hierbei sollen für die Bauelemente die allgemeinen Werte \(\mathrm {R}_1\), \(\mathrm {R}_2\), L, C verwendet werden.
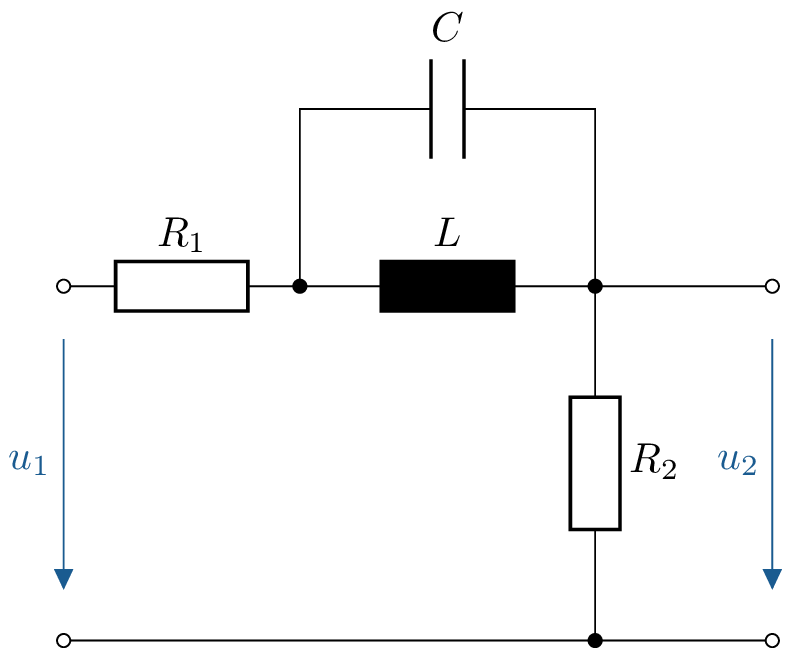
\begin {align*} \underline {F}(\mathrm {j}\omega ) = \frac {\underline {U}_2}{\underline {U}_1} \end {align*}
\begin {align*} \mathrm {u}_1 (t) = 5 \mathrm {V} \cdot \mathrm {cos} (2\pi \cdot 10 \mathrm {kHz} \cdot t) \end {align*}
gilt.
\begin {align*} \underline {F}(\mathrm {j}\omega ) & = \frac {\underline {U}_2}{\underline {U}_1} \\ &= \frac {R_2}{R_1 + \underline {Z}_L || \underline {Z}_C + R_2} &&\text {mit} \underline {Z}_L || \underline {Z}_C = \frac {\mathrm {j}\omega L \cdot \frac {1}{\mathrm {j}\omega C}}{\mathrm {j}\omega L - \mathrm {j}\frac {1}{\omega C}} = -\mathrm {j}\cdot \left (\frac {1}{\omega C - \frac {1}{\omega L}}\right )\\ &= \frac {R_2}{R_1 + R_2 - \mathrm {j}\left (\frac {1}{\omega C - \frac {1}{\omega L}}\right )} \end {align*}
\begin {equation*} \left | \underline {F}(\mathrm {j}\omega ) \right | = A(\omega ) = \frac {\mathrm {R}_2}{\sqrt {(\mathrm {R}_1 + \mathrm {R}_2)^2 + \left (\frac {1}{\omega \mathrm {C} - \frac {1}{\omega \mathrm {L}}}\right )^2}} \end {equation*} Die Parallelschaltung aus \(L\) und \(C\) verhält sich für \(\omega \to 0\) und für \(\omega \to \infty \) wie ein Kurzschluss, da jeweils eins der beiden Bauelemente in beiden Fällen eine Impedanz gegen Null besitzt. Daraus folgt für \(\omega \to 0\) und \(\omega \to \infty \): \begin {equation*} A(\omega \to 0) = A(\omega \to \infty ) = \frac {R_2}{R_1+R_2} \end {equation*} Im Resonanzfall (\(\omega = \omega _0 = \sqrt {\frac {1}{LC}}\)) heben sich die Admittanzen von \(L\) und \(C\) (Parallel-Schwingkreis) gegenseitig auf. Mit \(Y_C + Y_L \to 0\) folgt auch \(Z_L||Z_C \to \infty \) für \(\omega \to \omega _0\). \begin {equation*} A(\omega _0) = \frac {R_2}{\sqrt {(\mathrm {R}_1 + \mathrm {R}_2)^2 + \infty ^2}} = \frac {1}{\infty } = 0 \end {equation*}
Die Phase ergibt sich zu: \begin {align*} \varphi (\omega )&= \underbrace { \arctan \left (\frac {0}{R_2}\right ) }_{\varphi _{\text {Zähler}}} - \underbrace { \arctan \left (\frac {-\left (\frac {1}{\omega C - \frac {1}{\omega L}}\right )}{R_1 + R_2}\right ) }_{\varphi _{\text {Nenner}}} = \arctan \left (\frac {\frac {1}{\omega C - \frac {1}{\omega L}}}{R_1+R_2}\right ) \end {align*}
Mit: \begin {align*} \varphi (\omega \to 0) &= \arctan \left (0\right ) = 0\\ \varphi (\omega \to \infty ) &= \arctan \left (0\right ) = 0\\ \varphi (\omega _0) &= \arctan \left (\infty \right ) = \pm \frac {\pi }{2} \\ \varphi (\omega < \omega _0) &< 0\\ \varphi (\omega > \omega _0) &> 0 \end {align*}
Der Amplitudengang und Phasengang sind in folgendem Bode-Diagramm dargestellt.

\begin {align*} \underline {U}_2 &= \underline {F}(\mathrm {j}\omega ) \cdot \underline {U}_1 \\ u_2(t) &= A(\omega ) \cdot 5\,\mathrm {V} \cdot \cos \left (\omega t + \varphi (\omega )\right ) &&\text {mit} \omega = 2\pi \cdot 10\,\mathrm {kHz}\cdot \end {align*}
Der dargestellte Parallelschwingkreis soll untersucht werden.
\begin {align*} \underline {Y} &= \frac {1}{R} + \mathrm {j}\omega C + \frac {1}{\mathrm {j}\omega L} \\[2pt] \underline {Z} &= \frac {1}{\underline {Y}} = \frac {1}{\frac {1}{R} + \mathrm {j}\omega C + \frac {1}{\mathrm {j}\omega L}} \\[2pt] &= \frac {\frac {1}{R}-\mathrm {j}\cdot \left (\omega C - \frac {1}{\omega L}\right )}{\frac {1}{R^2} + \left (\omega C - \frac {1}{\omega L}\right )^2} \end {align*}
Die Gesamptimpedanz ist maximal bei Resonanzkreisfrequenz mit \(\underline {Z}(\omega _0) = R\).
\begin {align*} \Im \{\underline {Y}\} = \omega _0 C - \frac {1}{\omega _0 L} \overset {!}{=} 0 \Leftrightarrow \omega _0 &= \frac {1}{\sqrt {LC}} \Rightarrow f_0 = \frac {\omega _0}{2\pi }\\ |\underline {Z}(\omega _0)| = \frac {1}{\sqrt {\frac {1}{R^2} + \Big (\smash {\underbrace { \omega _0 C - \frac {1}{\omega _0 L} }_{={}{0}}}\Big )^2 } } &= \frac {1}{\sqrt {\frac {1}{R^2}}} = R \end {align*}
Grenzfrequenzen, Bandbreite: \begin {align*} {|\underline {Z}(\omega )| \overset {!}{=} \frac {R}{\sqrt {2}} \Leftrightarrow } \frac {1}{\sqrt {\frac {1}{R^2} + \left (\omega C - \frac {1}{\omega L}\right )^2}} &= \frac {R}{\sqrt {2}} \\ \frac {R}{\sqrt {1 + R^2\cdot \left (\omega C - \frac {1}{\omega L}\right )^2}} &= \frac {R}{\sqrt {2}} \\ 1 + R^2\cdot \left (\omega C - \frac {1}{\omega L}\right )^2 &= 2 \\ \left (\omega C - \frac {1}{\omega L}\right )^2 &= \frac {1}{R^2} \\ \omega C - \frac {1}{\omega L} &= \pm \frac {1}{R} \\ \omega ^2 LC \pm \omega \cdot \frac {L}{R} - 1 &= 0 \\ \omega ^2 \pm \omega \cdot \frac {1}{RC} - \frac {1}{LC} &= 0 \\ x^2 + p \cdot x + q &= 0 \vphantom {\frac {1}{LC}} \end {align*}
\begin {align*} x_{1,2} &= -\frac {p}{2} \pm \sqrt {\left (\frac {p}{2}\right )^2 - q} \\ \Rightarrow \omega &= \pm \frac {1}{2 \cdot RC} \pm \sqrt {\frac {1}{(2 \cdot RC)^2} + \frac {1}{LC}}\\ \frac {1}{2 \cdot RC} &= 1,6667 \cdot 10^3\ \mathrm {s}^{-1} \qquad \frac {1}{LC} = 5 \cdot 10^6\ \mathrm {s}^{-2} \\[4pt] \omega &= \pm 1,6667 \cdot 10^3\ \mathrm {s}^{-1} \pm 2,7889 \cdot 10^3\ \mathrm {s}^{-1} \\[4pt] \omega {g,o} &= 4,4556 \cdot 10^3 \mathrm {s}^{-1} \qquad f_{g,o} = 709,12\ \mathrm {Hz}\\ \omega {g,u} &= 1,1222 \cdot 10^3 \mathrm {s}^{-1} \qquad f_{g,u} = 178,60\ \mathrm {Hz}\\[4pt] B &= f_{g,o} - f_{g,u} = 530,5\,\mathrm {Hz} \end {align*}
\begin {align*} B &= \frac {f_0}{Q} & \text {mit} Q &= \sqrt {\frac {C}{L}}\cdot R = \sqrt {\frac {1\ \mu \mathrm {F}}{200\ \mathrm {mH}}} \cdot 300\ \Omega = 0,6708 \\ B &= \frac {355,88\ \mathrm {Hz}}{0,6708} = 530,5\ \mathrm {Hz} & \text {mit} f_0 &= \frac {1}{2\pi \sqrt {LC}} = \frac {1}{2\pi \sqrt {200\ \mathrm {mH} \cdot 1\ \mu \mathrm {F}}} = 355,88\ \mathrm {Hz} \\ \end {align*}
\begin {equation*} \left (\omega C - \frac {1}{\omega L}\right )^2 = \bigg (\underbrace { \frac {\omega }{\omega _0} - \frac {\omega _0}{\omega } }_{=\vartheta (\omega ){,\ \vartheta ^2\ \text {symmetrisch um }\omega _0\text { bei faktorieller Änderung}}} \bigg )^2\cdot \frac {C}{L} \qquad \Longrightarrow \qquad \vartheta ^2(n\cdot \omega _0) = \vartheta ^2\left (\frac {1}{n}\cdot \omega _0\right ) \end {equation*}
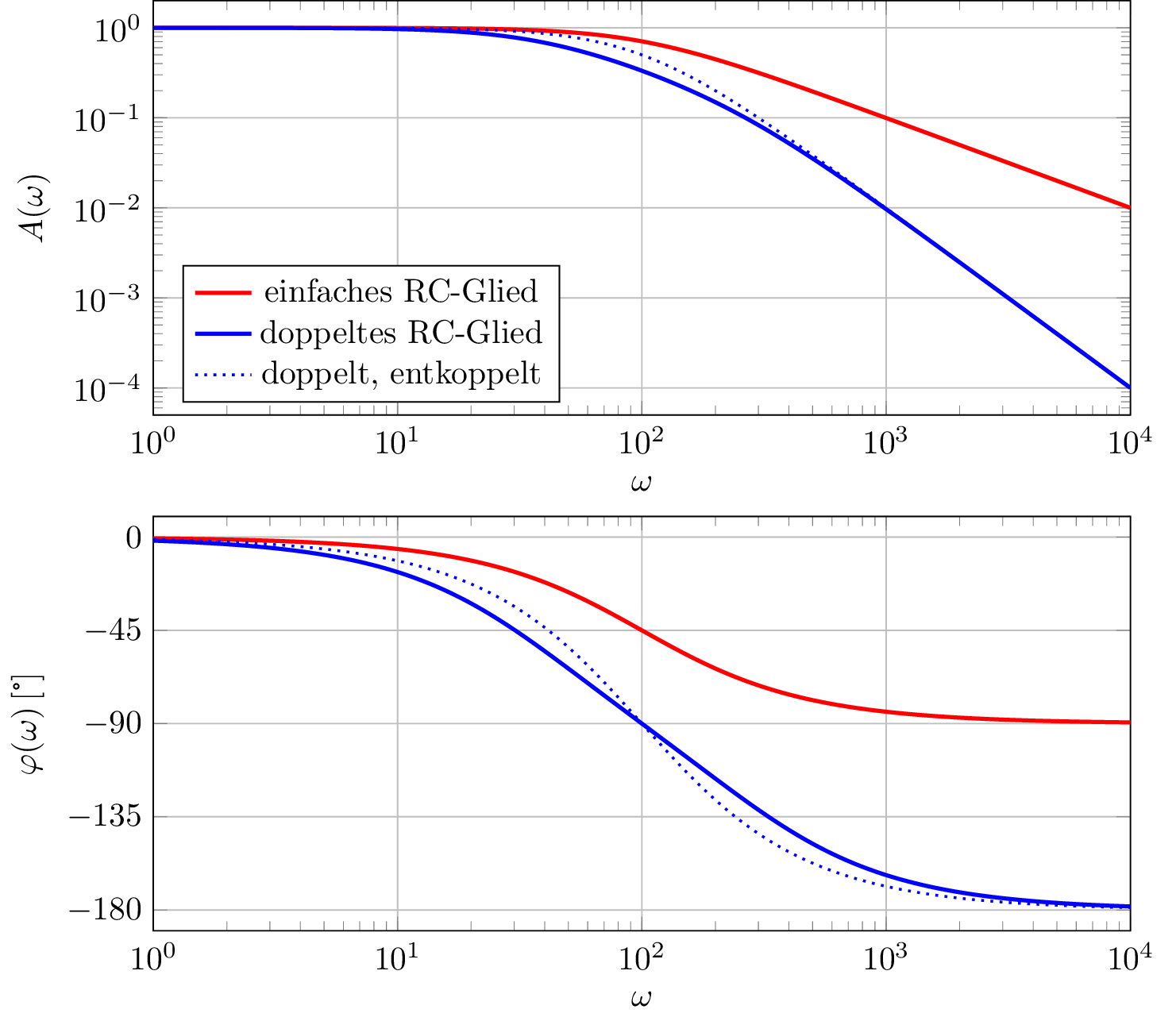
Für die untenstehende hintereinandergeschalteten RC-Glieder gilt \(R_1 = R_2 = R = 1000\,\Omega \) und \(C_1 = C_2 = C = 1\,\mu \mathrm F\).
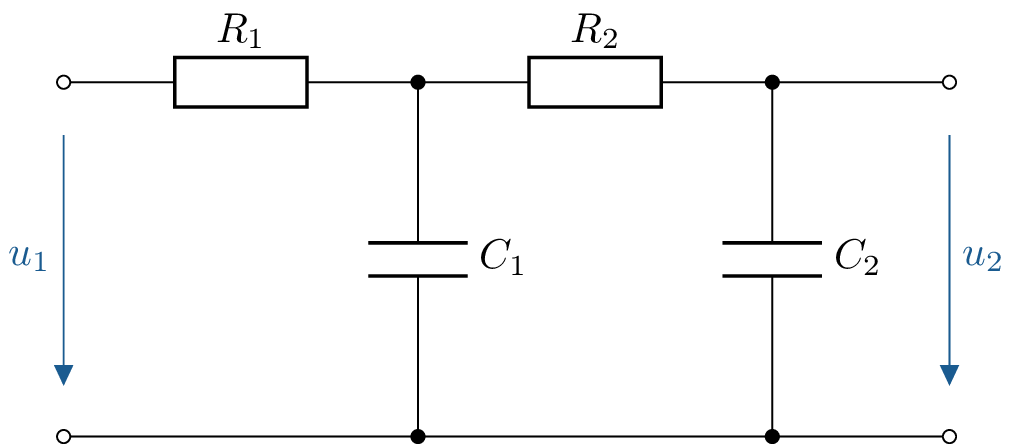
\begin {align*} \underline {F}(\mathrm {j}\omega ) &= \frac {\underline {U}_2}{\underline {U}_1} = \frac {\underline {U}_2}{\underline {U}_m} \cdot \frac {\underline {U}_m}{\underline {U}_1}\\ \frac {\underline {U}_m}{\underline {U}_1} &= \frac {\underline {Z}_{\mathrm {ers}}}{R + \underline {Z}_{\mathrm {ers}}} = \frac {1}{\frac {R}{\underline {Z}_{\mathrm {ers}}} + 1}\\ \underline {Z}_{\mathrm {ers}} &= \left ( R + \frac {1}{\mathrm {j}\omega C} \right ) \bigg |\bigg |\, \frac {1}{\mathrm {j}\omega C} = \left ( \frac {1}{R + \frac {1}{\mathrm {j}\omega C}} + \mathrm {j}\omega C\right )^{-1}\\ \frac {\underline {U}_m}{\underline {U}_1} &= \frac {1}{R \cdot \left (\frac {1}{R + \frac {1}{\mathrm {j}\omega C}} + \mathrm {j}\omega C\right ) + 1} \\ &= \frac {1}{\frac {R\cdot \mathrm {j}\omega C}{R\cdot \mathrm {j}\omega C + 1} + R\cdot \mathrm {j}\omega C + 1} \\ &= \frac {R\cdot \mathrm {j}\omega C + 1}{R\cdot \mathrm {j}\omega C + \left ( R\cdot \mathrm {j}\omega C + 1 \right )^2} \\ &= \frac {R\cdot \mathrm {j}\omega C + 1}{R\cdot \mathrm {j}\omega C - R^2\omega ^2 C^2 + 2\cdot \mathrm {j}\omega C R + 1 } \\ &= \frac {1}{1 - \omega ^2 C^2 R^2 + \mathrm {j}3\omega C R} \\ &= \frac {1 + \mathrm {j}\Omega }{1 - \Omega ^2 + \mathrm {j}3\Omega } \qquad \text {mit} \qquad \Omega = \omega C R\\[4pt] \frac {\underline {U}_2}{\underline {U}_m} &= \frac {\frac {1}{\mathrm {j}\omega C}}{R + \frac {1}{\mathrm {j}\omega C}} = \frac {1}{1 + \mathrm {j}\omega C R} = \frac {1}{1 + \mathrm {j}\Omega }\\[4pt] \frac {\underline {U}_2}{\underline {U}_1} &= \frac {\underline {U}_2}{\underline {U}_m} \cdot \frac {\underline {U}_m}{\underline {U}_1} = \frac {1}{1 + \mathrm {j}\omega C R} = \frac {1}{1 + \mathrm {j}\Omega } \cdot \frac {1 + \mathrm {j}\Omega }{1 - \Omega ^2 + \mathrm {j}3\Omega } \\ &= \frac {1}{1 - \Omega ^2 + \mathrm {j}3\Omega } = \frac {1}{1 - (\omega C R)^2 + \mathrm {j}3\omega C R} \end {align*}
Vergleich einfacher Tiefpass: \begin {align*} \underline {F}(\mathrm {j}\omega ) = \frac {\frac {1}{\mathrm {j}\omega C}}{R + \frac {1}{\mathrm {j}\omega C}} = \frac {1}{1 + \mathrm {j}\omega C R} = \frac {1}{1 + \mathrm {j}\Omega } \end {align*}
Wegen Kopplungseffekten kann der Frequenzgang des einfachen Tiefpasses bei Serienschaltung nicht einfach multipliziert werden.
Die Dämpfung im Sperrbereich beträgt bei 2. Ordnung (blau) das doppelte (\(40\,\mathrm {dB}/\mathrm {Dek}\)) im Vergleich zur 1. Ordnung (rot) (\(20\,\mathrm {dB}/\mathrm {Dek}\)). Die Phasenverschiebung reicht von \(0^\circ \) bis \(-180^\circ \) bei 2. Ordnung, im Gegensatz zur 1. Ordnung, die nur von \(0^\circ \) bis \(-90^\circ \) reicht. Die Grenzfrequenz verschiebt sich durch die höhere Dämpfung nach links (kleiner für 2. Ordnung).
Gegeben ist die Serienschaltung aus einer Induktivität \(L = 10\,\mathrm {mH}\) und einem Widerstand \(R = 5\,\mathrm {k}\Omega \) bei einer variablen Frequenz mit \(f_\mathrm {min} = 5\,\mathrm {kHz}\) und \(f_\mathrm {max} = 50\,\mathrm {kHz}\).
a) 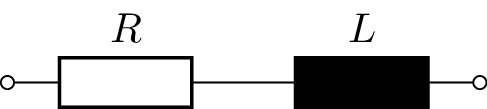 \begin {align*} f&=5\,\mathrm {kHz} ... 50\,\mathrm {kHz} & \underline {Z} &= R + \mathrm {j}\omega L \\ f_1 &= 5\,\mathrm {kHz} & \underline {Z}_1 &= 5\,\mathrm {k}\Omega + \mathrm {j} 314,16\,\Omega \\ f_2 &= 25\,\mathrm {kHz} & \underline {Z}_2 &= 5\,\mathrm {k}\Omega + \mathrm {j} 1570,8\,\Omega \\ f_3 &= 50\,\mathrm {kHz} & \underline {Z}_3 &= 5\,\mathrm {k}\Omega + \mathrm {j} 3141,6\,\Omega \end {align*}
\begin {align*} f&=5\,\mathrm {kHz} ... 50\,\mathrm {kHz} & \underline {Z} &= R + \mathrm {j}\omega L \\ f_1 &= 5\,\mathrm {kHz} & \underline {Z}_1 &= 5\,\mathrm {k}\Omega + \mathrm {j} 314,16\,\Omega \\ f_2 &= 25\,\mathrm {kHz} & \underline {Z}_2 &= 5\,\mathrm {k}\Omega + \mathrm {j} 1570,8\,\Omega \\ f_3 &= 50\,\mathrm {kHz} & \underline {Z}_3 &= 5\,\mathrm {k}\Omega + \mathrm {j} 3141,6\,\Omega \end {align*}
\(\underline {Z}\)-Ortskurve: \(\Re \{\underline {Z}\}=konst., \Im \{\underline {Z}\}=var.\\ \Rightarrow \) Gerade parallel zur Imaginärachse im I.
Quadranten.
b) Inversion von Geraden im I. Quadranten:
Halbkreis im IV. Quadranten. \begin {align*} \underline {Y}&=\frac {1}{\underline {Z}} & \underline {Y}&= \frac {1}{|\underline {Z}|} \cdot \mathrm {e}^{-\mathrm {j}\varphi _Z} \end {align*}
Maßstab so gewählt, dass \(\underline {Z}(0) = 5\,\mathrm {k}\Omega {}\hat {=}{} \underline {Y}(0) = 0,2\,\mathrm {mS}\).
Start des Halbkreises bei \(0,2\mathrm {mS}\) (\(\omega =0\)), Ende bei \(0\,\mathrm {mS}\) (\(\omega \to \infty \)) und Mittelpunkt bei
\(0,1\,\mathrm {mS}\).
Die Admittanzen sind abzulesen am jeweiligen Schnittpunkt
des gespiegelten Impedanzzeiger mit dem Halbkreis (Winkel
negiert, Spiegelung an x-Achse).
Die Admittanzkurve entspricht dem Kreisabschnitt zwischen \(\underline {Y}(f=5\,\mathrm {kHz})\) und \(\underline {Y}(f=50\,\mathrm {kHz})\).
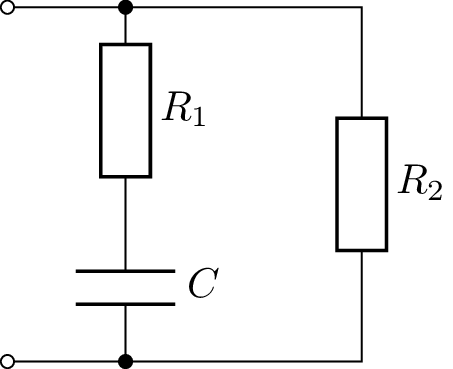
Die Admittanz der hier gezeigten Schaltung soll untersucht werden.
Parallel zu einer Reihenschaltung aus dem Widerstand \(R_1\) und der
Kapazität \(C\) befindet sich ein zweiter Widerstand \(R_2\).
Die Bauteilwerte sind gegeben durch:
\(R_1(p) = p \cdot R_0\), \(R_0 = 5\,\Omega \), \(R_2 = 20\,\Omega \) und \(\omega C = 0,2\,\mathrm {S}\)
\begin {align*} \underline {Y} &= \frac {1}{R_2} + \frac {1}{R_1 + \frac {1}{\mathrm {j}\omega C}} \\[2pt] &= \frac {1}{R_2} + \frac {R_1 - \frac {1}{\mathrm {j}\omega C}}{R_1^2 - \left (\frac {1}{\mathrm {j}\omega C}\right )^2} \\[2pt] &= \frac {1}{R_2} + \frac {p \cdot R_0 + \mathrm {j} \frac {1}{\omega C}}{p^2 \cdot R_0^2 + \left (\frac {1}{\omega C}\right )^2} \\[2pt] &= \frac {1}{20\,\Omega } + \frac {p \cdot 5\,\Omega + \mathrm {j} \cdot 5\,\Omega }{p^2 \cdot 25\,\Omega ^2 + 25\,\Omega ^2} \\[2pt] &= 0,05\,\mathrm {S} + \frac {p + \mathrm {j}}{p^2 + 1} \cdot 0,2\,\mathrm {S} \end {align*}
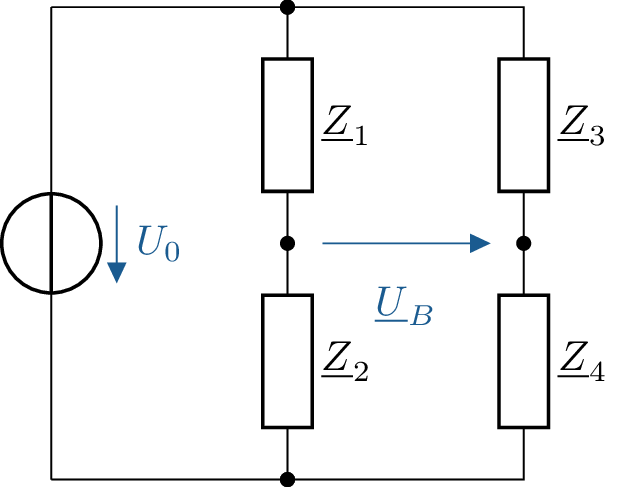
Untersucht wird die hier gezeigte Messbrückenschaltung.
...