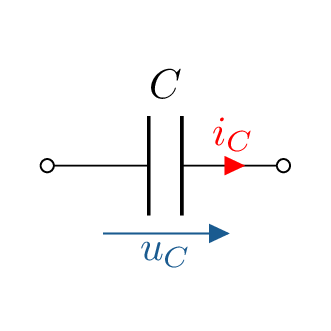Wiederholung
Um das frequenz- und zeitabhängige Verhalten elektrischer Netzwerke zu beschreiben, werden in diesem Kapitel kurz einige wichtige Grundlagen zusammengefasst.
Zur Bearbeitung vorrausgesetzt werden Kenntnisse über elektrische Grundgrößen, lineare passive Bauteile \(R\), \(L\) und \(C\), Netzwerkberechnungen, sowie die komplexe Wechselstromrechnung.
1 Frequenzabhängigkeit elektrischer Bauelemente
Rein ohmsche Widerstände \(R\) können elektrische keine Energie speichern. Spannungen und Ströme sind proportional zueinander und zu jedem Zeitpunkt in Phase. Das Verhalten ist zeit- und frequenzunabhängig.
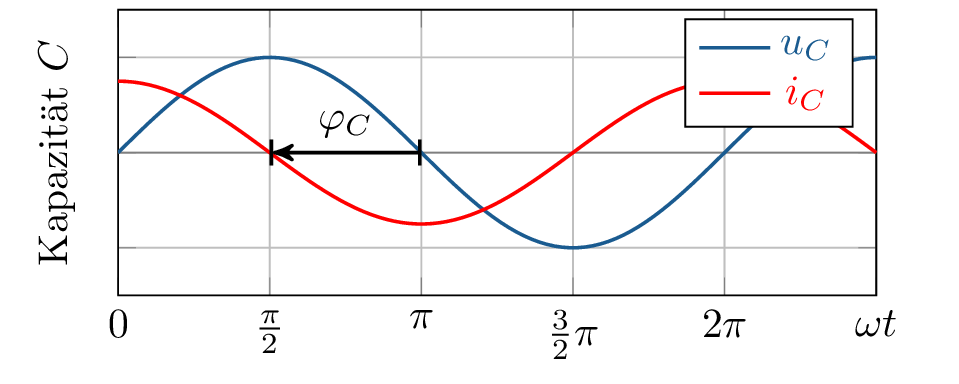
Induktivitäten \(L\) und Kapazitäten \(C\) hingegen können Energie speichern und abgeben. Dieser Vorgang ist inert (träge), benötigt also eine gewisse Zeit. Dadurch verhalten sie sich frequenzabhängig. Zwischen Strom und Spannung besteht jeweils eine Phasenverschiebung von \(\pm 90\ ^\circ \).
Abbildung 1 zeigt die Spannungs- und Stromverläufe für \(R\), \(L\) und \(C\) bei Erregung mit einer Wechselspannung \(u_q = U \cdot \sin (\omega t)\) zum Vergleich.
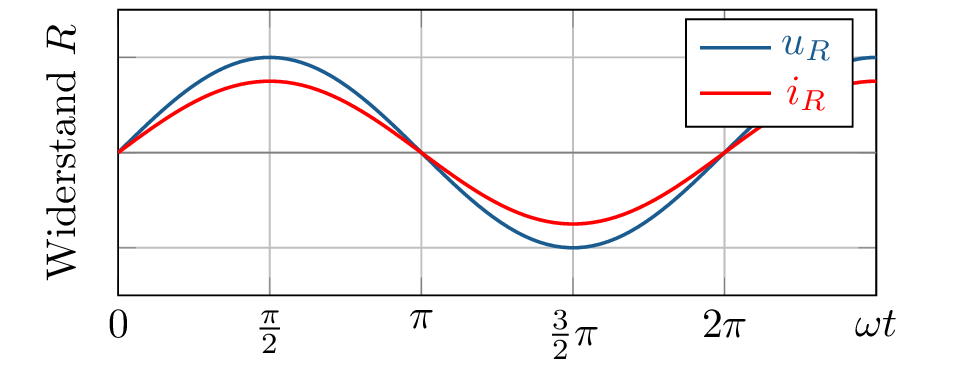
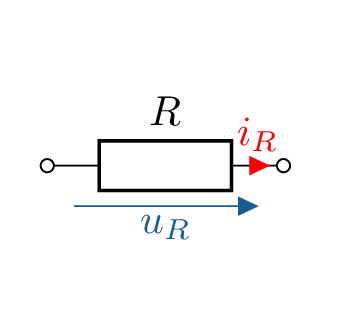
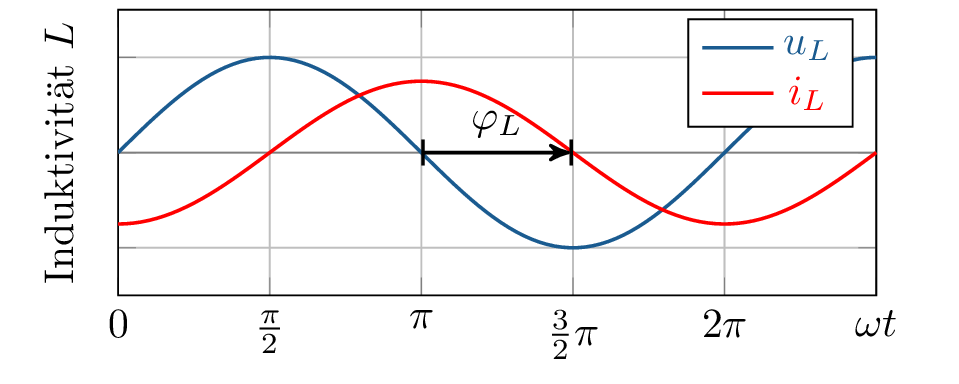
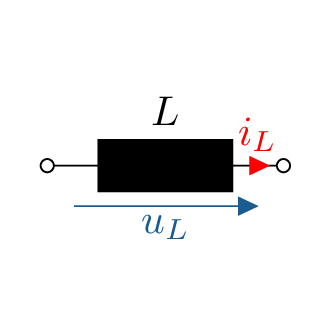
Aufgrund der Phasenverschiebung bei \(L\) und \(C\) oszilliert deren Leistung (Energieaufnahme und -abgabe), ist über eine Periode gemittelt jedoch immer null. Induktivitäten und Kapazitäten können daher keine Wirkleistung, sondern nur Blindleistung verrichten, weshalb sie auch Blindwiderstände genannt werden.
1.1 Verhalten von Induktivitäten und Kapazitäten
Induktivitäten als ideale Bauteile speichern durch den Effekt der (Selbst-)Induktion Energie im Magnetfeld. Kapazitäten als ideale Bauteile hingegen speichern Energie im elektrischen Feld. Beschrieben werden beide Effekte durch das Induktion- beziehungsweise das Gaußsche Gesetz.
Tabelle 1 listet die wichtigsten Unterschiede im Verhalten von Induktivitäten und Kapazitäten qulitativ als Übersicht auf.
| Induktivität | Kapazität | |
| Gesetz | Induktionsgesetz | Gaußsches Gesetz |
| Energiespeich. | im Magnetfeld | im Elektr. Feld |
| stetig | Strom | Spannung |
| bei Gleichspg. | Kurzschluss | offen |
| bei Hochfreq. | offen | Kurzschluss |
Die (Selbst-)Induktivität \(L\) als Eigenschaft kann vereinfacht als „Trägheit “des Stroms betrachtet werden. Ströme in Induktivitäten sind stetig und eilen der Spannung hinterher. Bei hohen Frequenzen sperrt die Induktivität, bei Gleichspannung verhält sie sich wie ein Kurzschluss.
Die Kapazität \(C\) kann dem gegenüber vereinfacht als „Trägheit “der Spannung betrachtet werden. Spannungen in Kapazitäten sind stetig und eilen dem Strom hinterher. Bei Gleichstrom sperrt die Kapazität, bei hohen Frequenzen verhält sie sich wie ein Kurzschluss.


Abbildung 2 zeigt reale Bauteile, die Induktivitäten und Kapazitäten realisieren. Gezeigt sind eine Spule (Induktivität) und ein Kondensator (Kapazität).
1.2 Vergleich der linearen Zweipole \(R\), \(L\) und \(C\)
2 zeigt eine Gegenüberstellung der Größen \(R\), \(L\) und \(C\) und fasst deren wichtigsten Eigenschaften zusammen.
| Größe | Allgemein | El. Widerstand | Induktivität | Kapazität |
 |  | 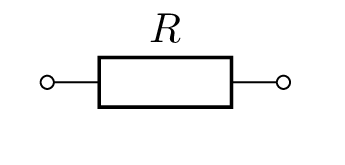 | 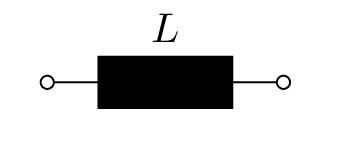 | 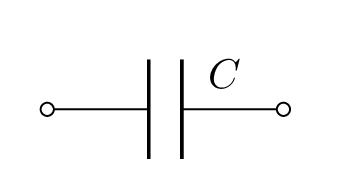 |
| Einheit | \( \left [\textit {Form.z.}\right ] = \mathrm {Einheit} \) | \( \left [R\right ] = \Omega \ \text {(Ohm)} \) | \( \left [L\right ] = \mathrm {H}\ \text {(Henry)} \) | \( \left [C\right ] = \mathrm {F}\ \text {(Farad)} \) |
| Zeitbereich \(\vphantom {\bigg |}\) | \( \frac {\mathrm{d} }{\mathrm {d}t} \) bzw. \( \int \mathrm {d}t \) | \( u_{\mathrm {R}} = R \cdot i_{\mathrm R} \) | \( u_{\mathrm {L}} = L \cdot \frac {\mathrm{d} }{\mathrm {d}t}\, i_{\mathrm {L}} \) | \( i_{\mathrm {C}} = C \cdot \frac {\mathrm{d} }{\mathrm {d}t}\, u_{\mathrm {C}} \) |
| Frequenzb. \(\vphantom {\bigg |}\) | \( \mathrm {j}\omega \) bzw. \( \frac {1}{\mathrm {j}\omega } \) | \( \underline {U_{\mathrm R}} = R \cdot \underline {I_{\mathrm R}} \) | \( \underline {U_{\mathrm L}} = \mathrm {j}\omega L \cdot \underline {I_{\mathrm L}} \) | \( \underline {I_{\mathrm C}} = \mathrm {j}\omega C \cdot \underline {U_{\mathrm C}} \) |
| Impedanz \(\vphantom {\bigg |}\) | \( \underline {Z} = \frac {\underline {U}}{\underline {I}} \) | \( \underline {Z}_{\mathrm R} = R \) | \( \underline {Z}_{\mathrm L} = \mathrm {j}\omega L \) | \( \underline {Z}_{\mathrm C} = -\mathrm {j}\frac {1}{\omega C} \) |
| Wirkanteil \(\vphantom {\bigg |}\) | \( R = \Re \{\underline {Z}\} \) | \( R = \frac {U}{I} \) | \( 0 \) | \( 0 \) |
| Blindanteil \(\vphantom {\bigg |}\) | \( X = \Im \{\underline {Z}\} \) | \( 0 \) | \( X_{\mathrm L} = \omega L \) | \( X_{\mathrm C} = -\frac {1}{\omega C}\) |
2 Zweitore (Vierpole)
Die Frequenzabhängigkeit von Eintoren (Zweipole) haben wir in Modul 3 bereits untersucht. Mithilfe der komplexen Wechselstromrechnung konnten wir den frequenzabhängigen Wechselstromwiderstand (Impedanz) \(\underline {Z}\) einzelner Eintore bestimmen. Durch Anwendung der komplexen Strom- und Spannungsteilerregel konnten wir auch die Gesamt-Impedanz linearer zweipoliger Netzwerke bestimmen. Das heißt für solche, welche nur aus linearen Bauteilen wie \(R\), \(L\) und \(C\) bestehen.
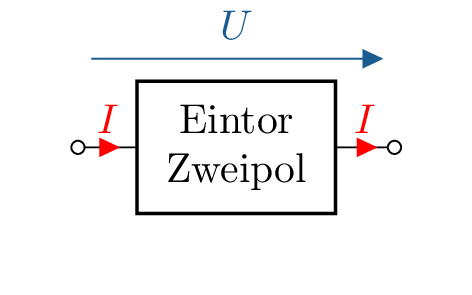
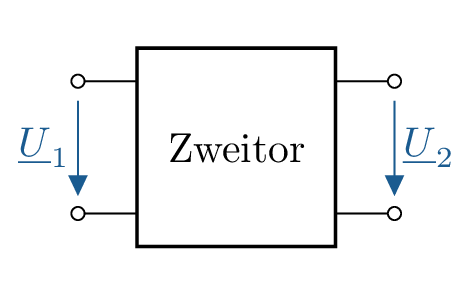
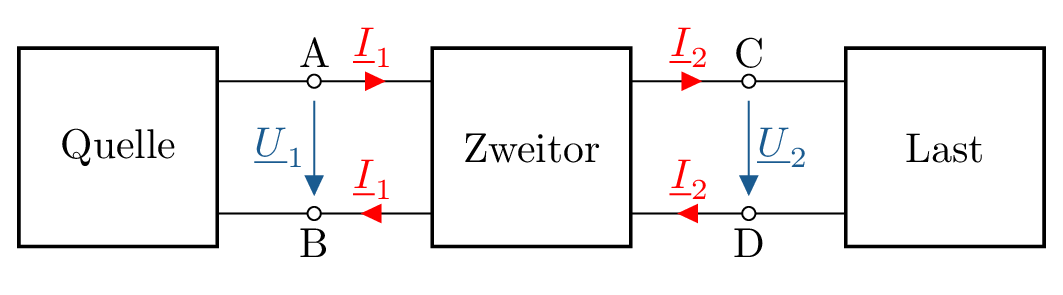
Zweitore (Vierpole) sind eine Erweiterung von Eintoren (Zweipolen). Sie verfügen über eine Eingangs- und eine Ausgangsseite mit jeweiligen Eingangs- und Ausgangsgrößen. Das Zweitormodell eignet sich gut zur Beschreibung von (frequenzabhängigen) Übertragungseigenschaften von elektrischen Netzwerken.
Im einfachsten Fall wird wie in 4 gezeigt, eine Quelle (Eintor) über ein Zweitor mit einer Last (Eintor) verbunden. Typische Zweitore sind beispielsweise Verstärker, Filter oder auch Transformatoren.