Frequenzgang, Amplitudengang, Phasengang

In diesem Kapitel beschäftigen wir uns mit dem Frequenzgang, Amplitudengang und Phasengang von Zweitoren. Diese dienen zur Beschreibung des frequenzvariablen Verhaltens elektrischer Netze in Form von Zweitoren wie in Abbildung 1 gezeigt. Am Beispiel einfacher passiver Filterschaltungen werden wir die Begriffe Frequenz-, Amplituden- und Phasengang einführen und deren Bedeutung und Anwendung erläutern.

1 Definition Frequenzgang, Amplitudengang und Phasengang

Der Frequenzgang \(\underline {F}(\mathrm {j}\omega )\), auch komplexer Amplitudengang genannt, beschreibt das Verhältnis von Ausgangs- zu Eingangssignal eines linearen zeitinvarainten Systems (LZI-System) bei sinusförmiger Anregung. Er bietet eine Möglichkeit frequenzabhängiges Verhalten von Zweitoren zu untersuchen, ist ein Spezialfall der Laplace-Übertragungsfunktion aus der Systemtheorie und wird wie folgt definiert:

\begin {equation} \underline {F}(\mathrm {j}\omega ) = \frac {\underline {U}_2}{\underline {U}_1}\label {eq:def:F} \end {equation}

Aufgrund der Linearität von LZI-Systemen bleiben Frequenz und Sinusform am Ausgang erhalten. Amplitude und Phase können sich in Abhängigkeit der Frequenz vom Eingang zum Ausgang ändern. Erkennbar ist dies insbesondere in der Schreibweise in Polarkoordinaten.

\begin {equation} \underline {F}(\mathrm {j}\omega ) = A(\omega )\cdot \mathrm e^{\mathrm j\varphi (\omega )}\label {eq:def:Fpolar} \end {equation} Der Amplitudengang \(A(\omega )\) beschreibt die relative Amplitudenänderung zwischen Aus- und Eingangsspannung und entspricht dem Betrag des Frequenzganges. Der Phasengang \(\varphi (\omega )\) hingegen, beschreibt die absolute Phasenänderung zwischen Aus- und Eingangsspannung und entspricht der Phase des Frequenzganges. Über \(\underline {F}(\mathrm {j}\omega )\) können wir beide wie folgt definieren:

\begin {align} \label {eq:def:A} A(\omega ) & = |\underline {F}(\mathrm {j}\omega )|& & = \sqrt {\left (\Re \{\underline {F}(\mathrm {j}\omega )\}\right )^2 + \left (\Im \{\underline {F}(\mathrm {j}\omega )\}\right )^2}& & = \frac {|\underline {U}_2|}{|\underline {U}_1|}\\ \label {eq:def:phi} \varphi (\omega ) & = \angle \underline {F}(\mathrm {j}\omega )& & = \arctan \left (\frac {\Im \{\underline {F}(\mathrm {j}\omega )\}}{\Re \{\underline {F}(\mathrm {j}\omega )\}}\right )& & = \angle \underline {U}_2 - \angle \underline {U}_1 \end {align}

2 Frequenzgang am Beispiel eines einfachen Tiefpass-Filters

Das Zweitor in Abbildung 2 stellt einen einfachen Tiefpass-Filter (kurz Tiefpass) dar. Der Name Tiefpass leitet sich von dem Verhalten her, dass Signale tiefer Frequenzen nahezu unverändert passieren, Signale hoher Frequenzen jedoch stark gedämpft (gefiltert) werden. Die Funktionsweise und das Verhalten des Tiefpasses lassen sich gut mittels einer Frequenzganganalyse veranschaulichen.

Der gezeigte Tiefpass besteht aus einer Serienschaltung aus \(R\) und \(C\) mit Eingangsspannung \(\underline {U}_1\) über beiden Elementen und Ausgangsspannung \(\underline {U}_2\) über \(C\). Da die Einzelelemente \(R\) und \(C\) lineare, zeitinvariante (LZI-)Bauteile sind, ist auch der daraus zusammen gesetzte Tiefpass ein LZI-System. Das bedeutet, dass bei Anregung der Schaltung mit einer sinusförmigen Eingangsspannung \(u_1(t)\) (links), die Ausgangsspannung \(u_2(t)\) (rechts) ebenfalls sinusförmig ist und die gleiche Frequenz besitzt wie die Eingangsspannung. \begin {equation} \begin {aligned} u_1(t)& = \hat {U}_1 \cdot \sin (\omega t)\\\xrightarrow {LZI}\ u_2(t)& = \hat {U}_2 \cdot \sin (\omega t + \varphi ) \end {aligned} \end {equation}Die LZI-Eigenschaft ist Voraussetzung zur Bestimmung des Frequenzganges und die Anwendung der komplexen Wechselstromrechnung. Zusätzliche Voraussetzung ist die Annahme einer sinusförmigen Anregung im eingeschwungenen Zustand, von der wir zwecks Analyse ausgehen. Statt der Ein- und Ausgangsspannung \(u_1(t)\) und \(u_2(t)\) im Zeitbereich betrachten wir die entsprechende komplexe Ein- und Ausgangsspannung \(\underline {U}_1\) und \(\underline {U}_2\) im Frequenzbereich wie im Schaltbild dargestellt.

Der Frequenzgang \(\underline {F}(\mathrm {j}\omega )\) entspricht nach Gleichung 1 dem komplexen Spannungsverhältnis von Ausgangs- zu Eingangsspannung \(\underline {U}_2/\underline {U}_1\). Gemäß komplexer Spannungsteilerregel entspricht das Spannungsverhältnis dem Verhältnis der Impedanz am Ausgang (Impedanz der Kapazität) und der Impedanz am Eingang (Summe der Impedanz von Kapazität und Widerstand), kurz \(\frac {\underline {Z}_C}{R + \underline {Z}_C}\).

Gleichung 4 zeigt den ermittelten Frequenzgang des Tiefpasses. Zur Vereinfachung wurden Nenner und Zähler rationalisiert, der Nenner sortiert und der Term (optional) in kartesische Koordinaten umgeformt. (Vergleich kommentierte Nebenrechnung ??): \begin {equation} \begin {aligned} \underline {F}(\mathrm {j}\omega ) & = \frac {\underline {U}_2}{\underline {U}_1} = \frac {\frac {1}{\mathrm {j}\omega C}}{R + \frac {1}{\mathrm {j}\omega C}} = \frac {1}{\mathrm {j}\omega CR + 1} \\ & = \frac {1}{1 + \mathrm {j}\omega CR} = \frac {1 - \mathrm {j}\omega CR}{1 + (\omega CR)^2} \end {aligned}\label {eq:tiefpass:frequenzgang} \end {equation}

Damit haben wir den \(\underline {F}(\mathrm {j}\omega )\) in Abhängigkeit von \(\omega \) und den Bauteilgrößen \(C\) und \(R\) ermittelt. Mittels Betragsbildung lässt sich daraus gemäß (??) der Amplitudengang und durch Phasenberechnung gemäß (??) der Phasengang bestimmen.

Zur Betragsbildung bietet sich die Form \(\frac {1}{1+\mathrm {j}\omega CR}\) an. Da der Betrag im Zähler direkt ablesbar \(1\) beträgt, muss nur der Betrag im Nenner bestimmen werden wie sie in (??) gezeigt ist. Alternativ kann auch die kartesische Form aus (4) in (??) eingesetzt werden.

Für den Phasengang \(\varphi (\omega )\) bietet sich die kartesische Schreibweise in der Form \(\frac {1-\mathrm {j}\omega CR}{1+(\omega CR)^2}\) an. In dieser lassen sich der Real- und Imaginärteil leicht ablesen. Der Nenner hat dabei als rein reelle Größe keinen Einfluss auf die Phasenlage wie in (??) gezeigt ist.

\begin {align} A(\omega ) &= |\underline {F}(\mathrm {j}\omega )| = \left |\frac {1}{1+\mathrm {j}\omega CR}\right | &&= \frac {\left |\qquad \!1\!\qquad \right |}{\left |1+\mathrm {j}\omega CR\right |} &= \frac {1}{\sqrt {1 + (\omega CR)^2}} \label {eq:tiefpass:ampli}\\ \varphi (\omega ) &= \angle \underline {F}(\mathrm {j}\omega ) = \angle \left (\frac {1 - \mathrm {j}\omega CR}{\redcancel {1+(\omega CR)^2}}\right ) &&= \arctan \left ( \dfrac { \dfrac {-\omega CR}{\redcancel {1+(\omega CR)^2}} }{ \dfrac {1}{\redcancel {1+(\omega CR)^2}} } \right ) &= \arctan \left (-\omega CR\right ) \label {eq:tiefpass:phase} \end {align}

Alternativ kann der Phasengang auch aus der nicht kartesischen Form des Frequenzganges bestimmt werden. Der Phasengang ergibt sich aus der Phasenlage des Zählers subtrahiert mit der Phasenlage des Nenners:

\begin {align} \varphi (\omega ) &= \angle \left (\frac {1}{1+\mathrm {j}\omega CR}\right ) = \underbrace {\arctan \left (\frac {0}{\redcancel {1}}\right )}_{\varphi _{Zaehler}}-\underbrace {\arctan \left (\frac {\omega CR}{\redcancel {1}}\right )}_{\varphi _{Nenner}} &= \arctan \left (-\omega CR\right ) \label {eq:tiefpass:phase:alternative} \end {align}

Die Herangehensweise bietet sich vor allem an, wenn sich Betrag und/oder Phase des Zählers direkt ablesen lassen. Dadurch kann ein Rechenschritt zum Umrechnen in kartesische Koordinaten gespaart werden.

Im folgenden Exkurs wird die seperate Betrachtung von Zähler und Nenner von Frequenzgängen näher erläutert:

Exkurs Berechnung komplexer Zahlen in (kartesischen) Descartes- und Polar-Koordinaten

Der Frequenzgang nimmt in der Regel die Form eines komplexen gebrochen rationalen Bruches an. Das bedeutet, dass sowohl Nenner als auch Zähler sich als komplexe Polynome darstellen lassen:

\begin {equation} \label {eq:def:F:komplexgebrochenrationalerbruch} \underline {F}(\mathrm {j}\omega ) = \frac {\underline {F}_Z(\mathrm {j}\omega )}{\underline {F}_N(\mathrm {j}\omega )} = \frac {a_n \omega ^n + \dots + a_1 \omega + a_0}{b_m \omega ^m + \dots + b_1 \omega + b_0} \qquad \text {mit} \qquad a_i, b_j \in \mathbb {C} \qquad n,m,\omega \in \mathbb {R} \end {equation}

Liegt \(\underline {F}(\mathrm {j}\omega )\) nun als komplexer Bruch vor mit Zähler und Nenner in kartesischen Koordinaten, so können wir \(A(\omega )\) und \(\varphi (\omega )\) durch seperate Betragsbildung und Phasenberechnung von Zähler und Nenner bestimmen. Hierfür werden die Formeln aus (??) und (??) für Zähler (Index \(Z\)) und Nenner (Index \(N\)) angewandt. Da Amplituden- und der Phasengang wie in (2) gezeigt die Polar-Koordinaten (Amplitude und Phase) des Frequenzganges darstellen ergibt sich folgendes Berechnungsschema:

\begin {align} \label {eq:def:F:bruch} \underline {F}(\mathrm {j}\omega ) & = \frac {\underline {F}_Z(\mathrm {j}\omega )}{\underline {F}_N(\mathrm {j}\omega )}& & = \frac {|\underline {F}_Z| \cdot \mathrm {e}^{\mathrm {j}\angle {\underline {F}_Z}}}{|\underline {F}_N| \cdot \mathrm {e}^{\mathrm {j}\angle {\underline {F}_N}}}& & = \frac {A_Z}{A_N} \cdot \mathrm {e}^{\mathrm {j} (\varphi _Z - \varphi _N)} \vphantom {\Bigg |}\\ \label {eq:def:A:bruch} A(\omega ) & = |\underline {F}(\mathrm {j}\omega )|& & = \frac {|\underline {F}_Z|}{|\underline {F}_N|}& & = \frac {A_Z}{A_N}& \vphantom {\Bigg |}\\ \label {eq:def:phi:bruch} \varphi (\omega ) & = \angle \underline {F}(\mathrm {j}\omega )& & = \angle {\underline {F}_Z} - \angle {\underline {F}_N}& & = \varphi _Z - \varphi _N \end {align}

Im Allgemeinen bietet sich für Multiplikationen und Divisionen komplexer Zahlen die Berechnung in Polarkoordinaten (mit Betrag und Argument) an. Eine Multiplikation/Division führt bei komplexen Zahlen zur Multiplikation/Division der Beträge und Addition/Subtraktion der Argumente. Bei Additionen und Subtraktionen eignet sich die kartesische Form mit Real- und Imaginärteil besser für Berechnungen, da diese direkt addiert/subtrahiert werden können.

3 Grenzverhalten am Beispiel eines einfachen Tiefpass-Filters

In diesem Kapitel wird das Grenzverhalten des Tiefpass-Filters 1. Ordnung aus dem vorigen Kapitel (s. Abbildung 2) für sehr hohe und sehr niedrige Frequenzen untersucht. Dazu werden die Grenzwerte des Amplitudengangs \(A(\omega )\) und des Phasengangs \(\varphi (\omega )\) bestimmt, sowie die Ergebnisse beschrieben, interpretiert und grafisch dargestellt.

Grenzwerte:

Für den Amplitudengang aus Gleichung ?? ergeben sich für \(f \rightarrow 0\) und \(f \rightarrow \infty \) die folgenden Grenzwerte:

\begin {align} &&A(\omega ) &=\frac {1}{\sqrt {1 + (\omega CR)^2}} & & & & &&\nonumber \\ && & & \lim _{\omega \rightarrow 0}A(\omega ) &=\frac {1}{1} & &=1 &&\label {eq:tiefpass:ampli:lim}\\ && & & \lim _{\omega \rightarrow \infty }A(\omega )&=\frac {1}{\sqrt {\infty }} & &=0 &&\nonumber \\\intertext {Für den Phasengang aus Gleichung \ref {eq:tiefpass:phase} ergeben sich analog dazu die Grenzwerte:}&&\varphi (\omega ) &=\arctan \left (-\omega CR\right )& & & & &&\nonumber \\ && & & \lim _{\omega \rightarrow 0}\varphi (\omega ) &=\arctan (0) & &=0^\circ &&\label {eq:tiefpass:phase:lim}\\ && & & \lim _{\omega \rightarrow \infty }\varphi (\omega ) &=\arctan (-\infty ) & &=-90^\circ &&\nonumber \end {align}

An Gleichung ?? ist zu erkennen, dass der Tiefpass bei sehr niedrigen Frequenzen kaum dämpft (\(A(\omega ) \rightarrow 1\)), bei sehr hohen Frequenzen hingegen stark dämpft (\(A(\omega ) \rightarrow 0\)).

An Gleichung ?? ist zu erkennen, dass der Tiefpass bei sehr niedrigen Frequenzen (bei kaum Dämpfung) kaum Phasenverschiebung aufweist (\(\varphi (\omega ) \rightarrow 0^\circ \)), bei sehr hohen Frequenzen (starke Dämpfung) hingegen eine Phasenverschiebung bis \(-90^\circ \) aufweist.

Erklärung des Grenzverhaltens anhand des Schaltbildes:

Das Grenzverhalten bezüglich Amplitudenänderung und Phasenverschiebung lässt sich gut anhand des Schaltbildes 2 erklären.

Im Grenzfall einer Gleichspannung (\(f=0\)) am Eingang sperrt die Kapazität (\(X_C \rightarrow \infty \)). Ihr Verhalten entspricht hier zwei offenen Klemmen, wodurch die gesamte Eingangsspannung am Ausgang \(U_2\) über der Kapazität \(C\) anliegt. Die relative Amplitudenänderung beträgt daher \(1\) (ungedämpft) und die Phasenverschiebung \(0^\circ \) (in Phase).

Bei sehr hohen Frequenzen (\(f\rightarrow \infty \)) verhält sich die Kapazität wie ein Kurzschluss (\(X_C \rightarrow 0\)). Damit geht die Ausgangsspannung gegen null (starke Dämpfung, \(A\rightarrow 0\)) und die Eingangsspannung liegt annäherend vollständig über \(R\) an. Eingangsspannung und Strom liegen dadurch näherungsweise in Phase. Die Phasenverschiebung von Ausgangsspannug über der Kapazität zu Eingangsspannung beträgt dadurch näherungsweise \(-90^\circ \).

Visualisierung:

Um eine Vorstellung des Verhaltens von Amplituden- und Phasengang zu bekommen, können wir die Funktionen graphisch darstellen.

Der Amplitudengang \(A(\omega )\) und der Phasengang \(varphi(\omega )\) sind in Abbildung 2a und 2b dargestellt. Beide Graphen sind mit linearen Skalen dargestellt, wobei die Skalierungen beider x-Achsen für \(\omega \left [\mathrm {Hz}\right ]\) identisch sind. Eine Veränderung des Faktors \(CR\) führt in linearer Darstellung lediglich zu einer Stauchung oder Streckung der Graphen in x-Richtung, weshalb auf eine explizite Angabe der Werte verzichtet wurde.

In Kapitel ?? wird die Darstellung des Frequenzganges mit logarithmischer Skala eingeführt. Auch die Definition der Grenzfrequenz \(f_g\) (respektive der Grenzkreisfrequenz \(\omega _g\)) zur Unterteilung des Frequenzbereichs in einen Durchlassbereich und einen Sperrbereich wird dort erläutert.

Exkurs zur Herleitung der Graphenform:

Die Graphenform des Amplitudengangs \(A(\omega )\) in linearer Darstellung lässt sich daran erklären, dass dieser sich für sehr niedrige Frequenzen (\(f \rightarrow 0\)) der waagrechten Gerade \(A=1\) annähert und für sehr hohe Frequenzen (\(f \rightarrow \infty \)) der Potenzfunktion \(\frac {1}{\omega CR}\) annähert. Abbildung 4 zeigt diese Näherungen für \(A(x)=\frac {1}{\sqrt {1+x^2}}\) mit \(x=\omega CR\).

Die Form des Phasenganges lässt sich leicht aus der Form einer (Arcus-)Tangensfunktion ableiten. Abbildung 5 zeigt die Tangensfunktion und dessen Umkehrfunktion Arcustangens, sowie deren jeweiligen Spiegelungen an der y-Achse in linearer Darstellung.

Die Umkehrung der jeweiligen Funktion ist durch Spiegelung des Graphen an der Winkelhalbierenden (schwarz gestrichelte Gerade) und Tausch der x- und y-Achse erreichbar, vorrausgesetzt die jeweilige Funktion ist stetig monoton wachsend oder stetig monoton fallend. Der Tangens ist daher zur Bildung des Arcustangens auf den Winkelbereich \(-90^\circ \) bis \(+90^\circ \) beschränkt bei einem Wertebereich von \(-\infty \) bis \(+\infty \). Aufgrund der nicht darstellbaren Polstellen ist der dargestellte Wertebereich auf \(-6\) bis \(+6\) beschränkt.

Der Phasengang des Tiefpass 1. Ordnung entspricht dem abgebildeten \(\arctan (-x)\) für \(x=\omega CR >0\). Da es physikalisch keine negativen Frequenzen gibt, gilt \(\omega >0 \rightarrow x>0\), wodurch der Wertebereich des Phasengangs nur den halben Wertebereich des Arcustangens abdeckt, also von \(-90^\circ \) bis \(0^\circ \).

4 Frequenzgang am Beispiel eines einfachen Hochpass-Filters

Ein Hochpass-Filter (kurz Hochpass) funktioniert ähnlich einem Tiefpass-Filter. Dem Namen entsprechend passieren beim Hochpass jedoch Signale hoher Frequenzen nahezu ungedämpft (ungefiltert), während Signale niedriger Frequenzen stark gedämpft (gefiltert) werden.

Abbildung 6 zeigt exemplarisch einen RC-Hochpass erster Ordnung, der im Folgenden näher untersucht wird. Der Hochpass besteht aus einer einfach Serienschaltung von Widerstand \(R\) und Kapazität \(C\). Die Eingangsspannung \(\underline {U}_1\) liegt über \(R\) und \(C\) in Reihe an, während die Ausgangsspannung \(\underline {U}_2\) über \(R\) abgegriffen wird. Der Aufbau ist identisch mit dem RC-Tiefpass erster Ordnung, nur dass die Ausgangsspannung über \(R\) statt über \(C\) anliegt.

Die Herleitung des Frequenzganges erfolgt analog zum Vorgehen beim Tiefpass in Kapitel 2. Da es sich beim Hochpass um ein LZI-System handelt gilt: \begin {equation} \begin {aligned} u_1(t)& = \hat {U}_1 \cdot \sin (\omega t)\\ \xrightarrow {LZI} u_2(t)& = \hat {U}_2 \cdot \sin (\omega t + \varphi ) \end {aligned} \end {equation}

Das heißt, bei sinusförmiger Eingangsspannung \(u_1(t)\), ist auch die Ausgangsspannung \(u_2(t)\) sinusförmig mit gleicher Frequenz wie die Eingangsspannung.

Der Frequenzgang lässt sich dadurch gemäß Gleichung 1 bestimmen, indem die komplexe Wechselspannungen \(\underline {U}_2\) am Ausgang und \(\underline {U}_1\) am Eingang ins Verhältnis gesetzt werden. Dadurch erhalten wir:

\begin {equation} \begin {aligned} \underline {F}(\mathrm {j}\omega ) & = \frac {\underline {U}_2}{\underline {U}_1} = \frac {R}{R + \frac {1}{\mathrm {j}\omega C}} = \frac {1}{1 + \frac {1}{\mathrm {j}\omega CR}} \\ & = \frac {1}{1 - \mathrm {j}\ \frac {1}{\omega CR}} = \frac {1 + \mathrm {j}\ \frac {1}{\omega CR}}{1 + \frac {1}{(\omega CR)^2}} \end {aligned}\label {eq:hochpass:frequenzgang} \end {equation} Für den Amplitudengang \(A(\omega )\) und den Phasengang \(\varphi (\omega )\) ergeben sich die folgenden Gleichungen:

\begin {align} A(\omega ) &= |\underline {F}(\mathrm {j}\omega )| = \left |\frac {1}{1-\mathrm {j}\frac {1}{\omega CR}}\right | &= \frac {1}{\sqrt {1 + \frac {1}{(\omega CR)^2}}} \label {eq:hochpass:ampli}\\ \varphi (\omega ) &= \angle \underline {F}(\mathrm {j}\omega ) = \angle \left (\frac {1 + \mathrm {j}\frac {1}{\omega CR}}{1 + \frac {1}{(\omega CR)^2}}\right ) &= \arctan \left (\frac {1}{\omega CR}\right )\label {eq:hochpass:phase} \end {align}

5 Grenzverhalten am Beispiel eines einfachen Hochpass-Filters

Das Grenzverhalten des Hochpass-Filters 1. Ordnung aus Kapitel 4 wird in diesem Kapitel für sehr hohe und sehr niedrige Frequenzen untersucht. Die Grenzwertbestimmung des Amplitudengangs \(A(\omega )\) und des Phasengangs \(\varphi (\omega )\) erfolgt analog zu der des Tiefpass-Filter wie in Kapitel 3 beschrieben.

Grenzwerte:

Für den Amplitudengang aus Gleichung ?? ergeben sich die folgenden Grenzwerte für \(f \rightarrow 0\) und \(f \rightarrow \infty \):

\begin {align} &&A(\omega ) &=\frac {1}{\sqrt {1 + \left (\frac {1}{\omega CR}\right )^2}}& & && &&\nonumber \\ && && \lim _{\omega \rightarrow \infty }A(\omega ) &=\frac {1}{\infty } &&=0 &&\label {eq:tiefpass:ampli:lim}\\ && && \lim _{\omega \rightarrow 0}A(\omega ) &=\frac {1}{\sqrt {1}}&&=1 &&\nonumber \\\intertext {Für den Phasengang aus Gleichung \ref {eq:hochpass:phase} folgt analog dazu: }&&\varphi (\omega ) &=\arctan \left (\frac {1}{\omega CR}\right )& & && &&\nonumber \\ && && \lim _{\omega \rightarrow 0}\varphi (\omega ) &=\arctan (\infty ) &&=+90^\circ &&\label {eq:tiefpass:phase:lim}\\ && && \lim _{\omega \rightarrow \infty }\varphi (\omega ) &=\arctan (0) &&=0^\circ &&\nonumber \end {align}

Das heißt, bei sehr niedrigen Frequenzen dämpft der Hochpass stark (\(A(\omega ) \rightarrow 0\)) mit Phasenverschiebung bis \(+90^\circ \) und bei sehr hohen Frequenzen kaum (\(A(\omega ) \rightarrow 1\)) mit Phasenverschiebung bis \(0^\circ \).

Anhand des Schaltbildes 6 lässt sich dieses Grenzverhalten gut erklären. Bei Gleichspannung (\(f=0\)) sperrt die Kapazität, wodurch die gesamte Eingangsspannung über dieser abfällt.

Bei sehr kleinen Frequenzen (\(f \to 0\)) liegt die Eingangsspannung näherungsweise vollständig über der Kapazität an. Der Strom eilt der Eingangsspannung bis \(+90^\circ \) voraus, wodurch sich eine positive Phasenverschiebung bis \(+90^\circ \) zur Ausgangsspannung über dem Widerstand ergibt.

Bei sehr hohen Frequenzen (\(f \rightarrow \infty \)) verhält sich die Kapazität wie ein Kurzschluss, wodurch die Eingangsspannung näherungsweise vollständig über dem Widerstand am Ausgang anliegt. Dadurch sind Ausgangs- und Eingangsspannung näherungsweise gleich in Amplitude und in Phase.

Visualisierung:

Abbildung 7 zeigt den Amplitudengang \(A(\omega )\) und den Phasengang \(\varphi (\omega )\) des Hochpass 1. Ordnung in linearer Darstellung mit gleicher Skalierung und gleichem Wertebereich für die x-Achsen.

Eine logarithmische Darstellung des Frequenzganges wird in Kapitel ?? eingeführt.

6 Vergleich passive Filter 1. Ordnung mit \(L\) und \(R\)

Tiefpass und Hochpass lassen sich auch mit einer Induktivität \(L\) und einem Widerstand \(R\) realisieren. In Tabelle 1 sind die Schaltbilder für RL-Filter 1. Ordnung und ihre RC-Pendants gegenübergestellt. Zudem ist zu jedem Schaltbild die Formel für den Frequenzgang aufgeführt.

\(\vphantom {\Big |}\)	Tiefpass	\(\quad \underline {F}(\mathrm {j}\omega )\)	Hochpass	\(\quad \underline {F}(\mathrm {j}\omega )\)	\(\omega _g\)
RL		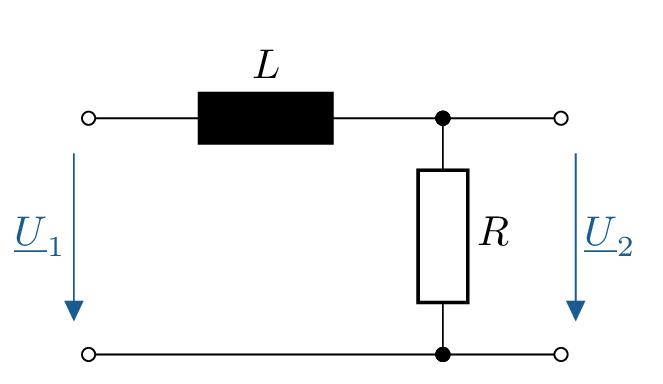\(\dfrac {1}{1+\mathrm {j} \omega \frac {L}{R}}\)		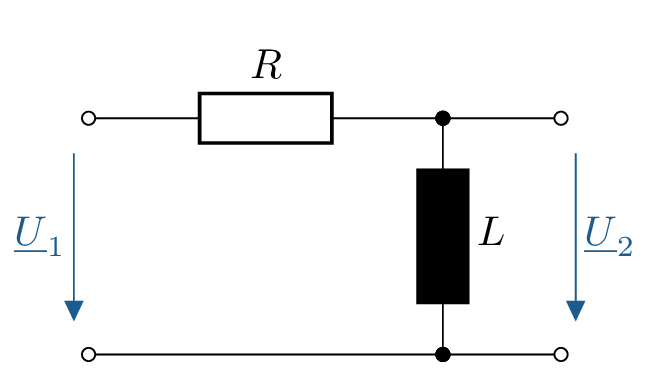\(\dfrac {1}{1-\mathrm {j}\frac {R}{\omega L}}\)	\(\dfrac {R}{L}\)
RC		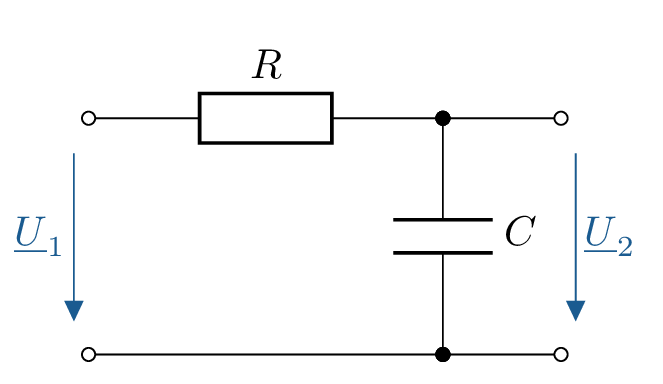\(\dfrac {1}{1+\mathrm {j}\omega 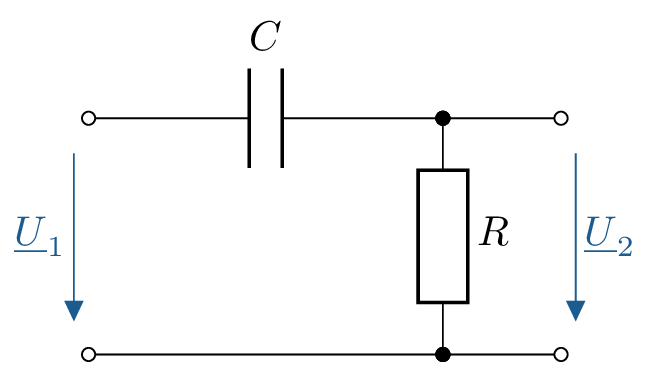RC}\)		\(\dfrac {1}{1-\mathrm {j}\frac {1}{\omega RC}}\)	\(\dfrac {1}{RC}\)

Im Vergleich der Schaltbilder ist zu erkennen, dass die RL- und RC-Varianten sich lediglich in der Anordnung von \(L\) und \(R\) beziehungsweise \(R\) und \(C\) unterscheiden. Die Frequenzgänge der RL- und RC-Varianten unterscheiden sich nur im Faktor \(\dfrac {L}{R}\) und \(RC\) vor \(\omega \) voneinander. Wie in Kapitel ?? noch näher erläutert wird, entspricht dieser Faktor dem Kehrwert der Grenzkreisfrequenz \(\omega _g\), welche vollständigkeitshalber mit in der Tabelle aufgeführt ist.

7 Beispiel Filterschaltung: Aufgabe

Beispiel 2: Filterschaltung: Lösung

Lösung a) Frequenzgang allgemein \begin {align*} \underline {F}(\mathrm {j}\omega ) &= \frac {R_1 || \underline {Z}_C}{R_2 + ( R_1 || \underline {Z}_C)} = \left .\frac {\frac {\frac {R_1}{\mathrm {j}\omega C}}{R_1 + \frac {1}{\mathrm {j}\omega C}}}{ R_2 + \frac {\frac {R_1}{\mathrm {j}\omega C}}{R_1 + \frac {1}{\mathrm {j}\omega C}}}\quad \right | \cdot \frac {R_1 + \frac {1}{\mathrm {j}\omega C}}{R_1 + \frac {1}{\mathrm {j}\omega C}} \\[+2pt] &= \frac {\frac {R_1}{\mathrm {j}\omega C}}{R_1\cdot R_2 + \frac {R_2}{\mathrm {j}\omega C}+\frac {R_1}{\mathrm {j}\omega C}} = \highlight {hfid_polar}{\frac {R_1}{R_1+R_2+\mathrm {j}\omega CR_1R_2}}[\hfofflowerb ][\hfoffupperb ][2] &&\hat {=}{} \frac {a+jb}{c+jd} & a,b,c,d &\in \mathbb {R} \\[+6pt] &= \highlight {hfid_kart}{\frac {R_1(R_1+R_2)-\mathrm {j}\omega CR_1^2R_2}{(R_1+R_2)^2+(\omega CR_1R_2)^2}}[\hfofflowerb ][\hfoffupperb ][3] \quad \text {(kartesisch)} &&\hat {=}{} \frac {a'+jb'}{c'} & a',b',c' &\in \mathbb {R} \end {align*}

\begin {align*} &\text {Betrag:}& |A(\omega )| &= \frac {R_1}{\sqrt {(R_1+R_2)^2+(\omega CR_1R_2)^2}}& &\text {mit}& |\underline {F}(\mathrm {j}\omega )| &= \frac {\sqrt {a^2+b^2}}{\sqrt {c^2+d^2}}\\ &\text {Phase:}& \varphi (\omega ) &= \arctan \left (\frac {-\omega C R_1^2R_2}{R_1(R_1+R_2)}\right )& &\text {mit}& \varphi (\omega ) &= \arctan \left (\frac {b'}{a'}\right )\\[+2pt] && &= \arctan \left (\frac {-\omega C R_1R_2}{R_1+R_2}\right )\\[-4pt] &\text {Altern.:}& \varphi (\omega ) &= \arctan (0) - \arctan \left (\frac {\omega CR_1R_2}{R_1+R_2}\right )& &\text {mit}& \varphi (\omega ) &= \overbrace {\varphi _{Z}}^{\mathclap {\scriptscriptstyle {\arctan (\frac {b}{a})}\ \ }} - \overbrace {\varphi _{N}}^{\mathclap {\ -\ \scriptscriptstyle {\arctan (\frac {d}{c})}}} \end {align*}

Lösung b) Grenzverhalten und Skizze

\(A(\omega ) = \frac {R_1}{\sqrt {(R_1+R_2)^2+(\omega CR_1R_2)^2}}\)

\(\ \ \ \ \lim \limits _{\omega \to 0} A(\omega ) = \frac {R_1}{R_1+R_2} = 0,9\)

\(\ \ \ \ \lim \limits _{\omega \to \infty } A(\omega ) = \frac {R_1}{\infty } = 0\)

\(\varphi (\omega ) = \arctan (-\frac {\omega CR_1R_2}{R_1+R_2})\)

\(\lim \limits _{\omega \to 0} \varphi (\omega ) = \arctan (0) = 0\)

\(\lim \limits _{\omega \to \infty } \varphi (\omega ) = \arctan (-\infty ) = -90^\circ \)

Lösung c) Bestimmten Arbeitspunkt ermitteln

Ges.: Frequenz \(f_{1}\) bei der \(\hat {U}_2 = \frac {1}{2}\hat {U}_1\) und Phasenverschiebung \(u_2\) zu \(u_1\) bei \(f_1\):\begin {align*} A(\omega _1) &= \frac {R_1}{\sqrt {(R_1+R_2)^2+(\omega CR_1R_2)^2}} \overset {!}{=} \frac {1}{2} & &\text {mit}& A(\omega ) = \frac {U_2}{U_1} = \frac {\hat {U}_2}{\hat {U}_1} \overset {!}{=} \left .\frac {1}{2}\right |_{f=f_1} \\[+2pt] &\Rightarrow \frac {(R_1+R_2)^2 + (\omega _1 CR_1R_2)^2}{R_1^2} = 4 & &\Rightarrow & (R_1+R_2)^2 + (\omega _1 C R_1R_{\mathrm {C}})^2 = 4R_1^2 \\ &\Rightarrow (\omega _1 CR_1R_2)^2 = 4R_1^2 - (R_1+R_2)^2 & &\Rightarrow & \omega _1 = \pm \frac {\sqrt {4R_1^2 - (R_1^2 + 2R_1R_2 + R_2^2)}}{CR_1R_2} \\[+2pt] \omega _1 &= 1,3304\cdot 10^4\ \frac {1}{\mathrm {s}},\ f_1 = 2,117\ \mathrm {kHz} & &\text {mit}& \omega _1 < 0 \text { unphysikalisch},\ f=\frac {\omega }{2\pi } \\ \varphi (\omega _1) &= \arctan (-1,4967) = -56,25^\circ & &\text {mit}& \varphi (\omega ) = \arctan \left (\frac {\Im \{\underline {F}\}}{\Re \{\underline {F}\}}\right ) \end {align*}