Im Modul 8
Logarithmische Darstellung, Frequenzgang, Grenzfrequenz
OrtskurvenIn der Elektrotechnik und Nachrichtentechnik werden häufig logarithmische Skalen verwendet, um den Frequenzgang von Filtern und Verstärkern darzustellen. Die logarithmische Darstellung ermöglicht eine bessere Übersicht über das Verhalten des Systems im gesamten Frequenzbereich.
Abbildung 1 zeigt zwei Comic-Strips von XKCD, die die Vorteile der logarithmischen Darstellung humorvoll darstellen.
In diesem Kapitel werden wir uns mit der logarithmischen Darstellung von Frequenzgängen in Form sogenannter Bode-Diagramme beschäftigen. Zur Beschreibung des Frequenzganges einfacher Filterschaltungen werden die Einheit Dezibel, sowie die Grenzfrequenz und die Ordnung von Filtern definiert. Darüber hinaus werden Bandpass- und Bandsperrfilter vorgestellt.
Lernziele: Logarithmische Darstellung, Frequenzgang
Studierende lernen:
In der logarithmischen Darstellung wird eine logarithmische Skala für eine oder mehrere Achsen verwendet. Eine lineare Zunahme von abzubildenden Werten korrespondiert hierbei mit einer logarithmischen Zunahme der Distanz auf der Skala. Anschaulicher im Umkehrschluss: Bei linearer Zunahme der Distanz auf der Skala steigt die Potenz der abzubildenden Werte im selben Maß linear an.
Logarithmische Skalen bieten sich im Allgemeinen an, um Wertebereiche über mehrere Größenordnungen darzustellen. Eine Besonderheit in der doppelt logarithmischen Darstellung ist, dass Potenzfunktionen als Geraden dargestellt werden. Abbildung 2 zeigt zum Vergleich mehrerer Potenzfunktionen in linearer Darstellung (links) und in doppelt-logarithmischer Darstellung mit Basis \(10\) (rechts).
Der Exponent einer Potenzfunktion entspricht in doppelt-logarithmischer Darstellung der Steigung der Geraden. Eine Verschiebung in y-Richtung entspricht einem Vorfaktor \(a\) für die Funktion \(f(x)\), eine Verschiebung in x-Richtung einem Vorfaktor \(x_{\mathrm {off}}\) für x in der Funktion. Durch diese Eigenschaften eignet sich die logarithmische Darstellung besonders zur Darstellung von Amplitudengängen.
Dezibel ist eine Hilfsmaßeinheit zur Kennzeichnung dekadisch-logarithmischer Verhältnisse zweier Größen. Verwendung findet es u.A. in der Signaltheorie und Nachrichtentechnik, beispielsweise um die Verstärkung/Dämpfung eines Bauteils oder einer Signalstrecke anzugeben. Ein Dezibel \([\mathrm {dB}]\) entspricht dem zehnfachen der Basiseinheit Bel \([\mathrm {B}]\).
Definiert ist das Bel als Kennzeichnung des dekadisch-logarithmischen Verhältnisses (Symbol \(Q\)) zweier einheitengleicher Leistungsgrößen (Index \(P\)) wie in Gleichung ?? gezeigt ist. In Zusammenhang mit Spannung oder Strom als sogenannte Leistungswurzelgrößen (ehemals Feldgrößen, Index \(F\)) kann das (Dezi-)Bel in linearen Systemen ebenfalls verwendet werden wie in Gleichung ?? gezeigt ist. Die Umrechnung basiert auf der Proportionalität von \(P\sim U^2\) beziehungsweise \(P\sim I^2\), woraus sich der Faktor \(2\) ergibt.
\begin {align} &\textrm {Leistungsgrößen }(\textrm {z.B. }P,\ W)& Q_{\mathrm {(P)}} &= \mathrm {log}\frac {P_2}{P_1}\ \operatorname {B} = 10\cdot \mathrm {log}\frac {P_1}{P_2}\,\mathrm {dB} && \label {eq:def:dezibel:leistung}\\ &\textrm {Leistungswurzelgr.}(\textrm {z.B. }U,\ I)& Q_{\mathrm {(R)}} &= \mathrm {log}\frac {U_2^2}{U_1^2}\ \operatorname {B} = 20\cdot \mathrm {log}\frac {U_1}{U_2}\,\mathrm {dB} && \label {eq:def:dezibel:wurzel} \end {align}
Die Angabe \(Q\) in \(\mathrm {dB}\) beschreibt hier die Verstärkung eines Systems von Eingangs- (Index \(1\)) zu Ausgangssignal (Index \(2\)). Tabelle 1 zeigt für typische Dezibelwerte zugehörige Spannungsverhältnisse \(\frac {U_2}{U_1}\) und Leistungsverhältnisse \(\frac {P_2}{P_1}\). Eine Änderung um \(6\mathrm {dB}\) entspricht auf die zweite Nachkommastelle gerundet genau dem Faktor \(2\) für Spannungen und auf die erste Nachkommastelle gerundet genau dem Faktor \(4\) für Leistungen.
| Leist.wurz.gr. | \(\frac {U_2}{U_1}\) | \(\frac {1}{\sqrt {2}}\) | \(1\) | \(\sqrt {2}\) | \(2\) | \(\sqrt {10}\) | \(10\) | \(20\) | \(100\) |
| Leistungsgrößen | \(\frac {P_2}{P_1}\) | \(\frac {1}{2}\) | \(1\) | \(2\) | \(4\) | \(10\) | \(100\) | \(400\) | \(10.000\) |
| Verstärkung | \(Q_{\mathrm {dB}}\) | \(-3\,\mathrm {dB}\) | \(0\,\mathrm {dB}\) | \(+3\,\mathrm {dB}\) \(+6\,\mathrm {dB}\) | \(10\,\mathrm {dB}\) | \(20\,\mathrm {dB}\) | \(26\,\mathrm {dB}\) | \(40\,\mathrm {dB}\) | |
Dadurch, dass \(3\,\mathrm {dB}\) sehr präzise dem Faktor \(2\) bei Leistungen (Faktor \(\sqrt {2}\) bei Spannungen) entspricht, beziehungsweise \(6\,\mathrm {dB}\) dem Faktor \(4\), lassen sich relativ einfach Abschätzungen vornehmen. Im Vergleich zur SI-Einheit Neper, welches auf dem natürlichen Logarithmus basiert, hat sich das Dezibel daher als logarithmische Hilfsmaßeinheit in der Praxis durchgesetzt.
Faustformeln für Spannungsverhältnisse:
Exemplarisch ist in Abbildung 4 die logarithmische y-Achse für \(A(\omega )\) einmal einheitenlos (links) und einmal in \(\mathrm {dB}\) (rechts) angegeben mit Kennzeichnung der ganzzahligen Faktoren beziehungsweise Dezibelwerten aus obiger Fausformel.
Phänologisch gilt:
Für die Verstärkung respektive Dämpfung als physikalische Größen gilt, dass diese sich in \(\mathrm {dB}\) mit umgekehrtem Vorzeichen entsprechen. Üblich ist die Bezeichnungen \(G\) (von engl. Gain) für die Verstärkung von Bauteilen oder \(D\) (von engl. Damping) für deren Dämpfung. Beide Angaben werden typischerweise in \(\mathrm {dB}\) und falls nicht näher deklariert in Bezug auf Spannungspegel angegeben. In Datenblättern wird die Dämpfung in \(\mathrm {dB}\) teilweise auch mit negativem Vorzeichen angegeben.
Hoch- und Tiefpässe erlauben die Filterung von Eingangssignalen in Abhängigkeit von deren Frequenz wie in Kapitel ?? für einen Tiefpass und in Kapitel ?? für einen Hochpass gezeigt wurde.
Der Frequenzbereich der Amplitudengänge beider Filter wird unterteilt in einen Durchlassbereich und einen Sperrbereich. Als Abgrenzung dient die sogenannte Grenzfrequenz \(f_g\), respektive Grenz(kreis)frequenz \(\omega _g\). Definiert ist \(\omega _g\) über ein festgelegtes Verhältnis von effektiver Ausgangs- zu Eingangsspannung.
Im Falle einfacher Filterschaltungen gilt:
\begin {equation} \left .\frac {U_2}{U_1}\right \rvert _{\omega =\omega _g} := \frac {1}{\sqrt {2}} \leftrightarrow A(\omega _g) := \frac {1}{\sqrt {2}} \label {eq:def:grenzfrequenz} \end {equation}
Nach Tabelle 1 entspricht dies einer Dämpfung von \(3\mathrm {dB}\) respektive einer Verstärkung von \(-3\mathrm {dB}\). Die Ausgangsleistung beträgt bei \(\omega _g\) die Hälfte der Eingangsleistung.
Beispiel: Tiefpass erster Ordnung
Mit Gleichung ?? folgt für den RC-Tiefpass erster Ordnung für die Grenzkreisfrequenz: \begin {align} A(\omega ) &= \frac {1}{\sqrt {1 + (\omega CR)^2}} \nonumber \\ A(\omega _g) &= \frac {1}{\sqrt {1 + (\omega _g CR)^2}} \overset {!}{=} \frac {1}{\sqrt {2}} \nonumber \\ \mathrm{d}ots \Longrightarrow \omega _g &= \frac {1}{CR} \label {eq:tiefpass:grenzfrequenz} \end {align}
Die Grenzkreisfrequenz \(\omega _g\) entsprichtdem Kehrwert der Zeitkonstante \(\tau = CR\) des RC-Gliedes.
Der Frequenz-, der Amplituden- und der Phasengang des RC-Tiefpasses erster Ordnung aus Gleichung ??, ?? und ?? lassen sich normiert auf \(\omega _g\) darstellen. Dadurch ergeben sich bauteilunabhängig: \begin {align} &&F(\mathrm {j}\omega ) &\overset {\text {\tiny {\ref {eq:tiefpass:frequenzgang}}}}{=} \frac {1}{1+\mathrm {j}\omega CR} & &\overset {\text {\tiny {\ref {eq:tiefpass:grenzfrequenz}}}}{\Longrightarrow }& F(\mathrm {j}\omega ) &= \frac {1}{1+\mathrm {j}\left (\omega /\omega _{\mathrm {g}}\right )} &&\label {eq:tiefpass:normiert:frequenzgang}\\ &&A(\omega ) &\overset {\text {\tiny {\ref {eq:tiefpass:ampli}}}}{=} \frac {1}{\sqrt {1 + (\omega CR)^2 }} & &\overset {\text {\tiny {\ref {eq:tiefpass:grenzfrequenz}}}}{\Longrightarrow }& A(\omega ) &= \frac {1}{\sqrt {1 + \left (\omega /\omega _{\mathrm {g}}\right )^2 }} \label {eq:tiefpass:normiert:amplitudengang}\\ &&\varphi (\omega ) &\overset {\text {\tiny {\ref {eq:tiefpass:phase}}}}{=} -\arctan \left (\omega CR\right ) & &\overset {\text {\tiny {\ref {eq:tiefpass:grenzfrequenz}}}}{\Longrightarrow }& \varphi (\omega ) &= -\arctan \left (\omega /\omega _{\mathrm {g}}\right ) \label {eq:tiefpass:normiert:phasengang} \end {align}
Abbildung 3 zeigt den Amplitudengang in Abhängigkeit von \(\omega /\omega _g\). Neben dem realen Verlauf in rot, ist auch der Verlauf eines idealisierten Tiefpasses mit hoher Flankensteilheit in blau dargestellt.
Eine Änderung der Grenzfrequenz führt in linearer Darstellung zu einer Stauchung oder Streckung des Amplitudenganges entlang der Frequenzachse.
Beispiel: Hochpass erster Ordnung
Analog können wir die Grenzfrequenz für den RC-Hochpass erster Ordnung bestimmen:
\begin {equation} \begin {aligned} A(\omega _g) &= \frac {1}{\sqrt {1+ \left ( \frac {1}{\omega _g CR} \right )^2 }} \overset {!}{=} \frac {1}{\sqrt {2}} \\\mathrm{d}ots \Longrightarrow \omega _g &= \frac {1}{CR} \end {aligned} \end {equation}
Die Grenzfrequenz beider Filter ist also identisch bei gleichen Bauteilwerten \(R\) und \(C\). Für den Frequenzgang des Hochpasses ergibt sich analog zur Tiefpass-Variante:
\begin {align} F(\mathrm {j}\omega ) &= \frac {1}{1-\mathrm {j}\left (\omega _{\mathrm {g}}/\omega \right )} \label {eq:hochpass:normiert:frequenzgang}\\ A(\omega ) &= \frac {1}{\sqrt {1 + \left (\omega _{\mathrm {g}}/\omega \right )^2 }}\\ \varphi (\omega ) &= \arctan \left (\omega _{\mathrm {g}}/\omega \right ) \label {eq:hochpass:normiert:amplitudengang} \end {align}
Frequenzgänge werden typischerweise in Bode-Diagrammen dargestellt. Bode-Diagramme bestehen aus einer doppelt-logarithmischen Darstellung des Amplitudengangs und einer einfach-logarithmischen Darstellung des Phasengangs. Die x-Achse für die (Kreis-)frequenz wird in beiden Darstellung logarithmisch skaliert. Die y-Achse wird beim Amplitudengang logarithmisch und beim Phasengang linear skaliert.
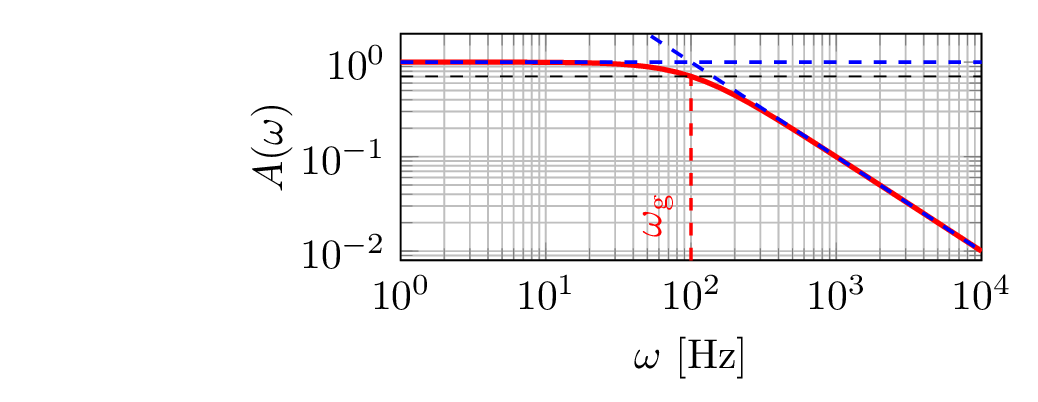
Abbildung 4 zeigt den Amplitudengang aus Gl. ?? eines Tiefpass 1. Ordnung als Bode-Diagramm. Durchlassbereich für \(\omega < \omega _g\) und Sperrbereich für \(\omega > \omega _g\) sind ebenso wie die Position für \(\omega =\omega _g\) gekennzeichnet. Die Frequenzangabe auf der x-Achse wurde auf die Grenzfrequenz normiert und erfolgt daher einheitenlos.
Gut zu erkennen ist die Unterteilung des Frequenzbereiches in Durchlass- und Sperrbereich durch die Grenzfrequenz. Der Verlauf des Amplitudenganges lässt sich in beiden Bereichen mithilfe der Asymptoten (Geraden) approximieren [blau gestrichelt]: \begin {align*} \lim _{\omega \to 0} A(\omega ) &= 1 & &\Longrightarrow & A(\omega ) &\approx 1 & &\text {für}& \omega &< \omega _g \text {(Durchlassbereich)} \\ \lim _{\omega \to \infty } A(\omega ) &= \frac {\omega _g}{\omega } & &\Longrightarrow & A(\omega ) &\approx \frac {\omega _g}{\omega } & &\text {für}& \omega &> \omega _g \text {(Sperrbereich)} \end {align*}
Die Steigung der Asymptote (Gerade) im Sperrbereich beträgt \(-20 \mathrm {dB}/\mathrm {Dek}\), aufgrund der Proportionalität von \(A(\omega ) \sim \omega ^{-1}\).
Die Näherung durch beide Asymptoten weicht maximal \(3 \mathrm {dB}\) für \(\omega = \omega _g\) vom realen Verlauf ab. Bei der Grenzfrequenz schneiden sich beide Asymptoten, was jedoch nicht allgemein für Filter gilt. Zur Konstruktion einer Skizze bieteten sich beide Asymptoten (Geraden) und der Punkt \(A(\omega _g) = 1/{1}{\sqrt {2}}\) an. Für die Skizze wird im Übergangsbereich von Faktor fünf größer oder kleiner der Grenzfrequenz (\(\frac {1}{5}\,\omega _g < \omega < 5\,\omega _g\)) ein Bogen von Asymptote durch \(A(\omega _g)= 1/{1}{\sqrt {2}}\) zu Asymptote gezeichnet.
Eine Veränderung der Grenzfrequenz führt im Bode-Diagramm zu einer Verschiebung entlang der Frequenz-Achse. Dies gilt für den Amplituden- als auch für den Phasengang, da die Frequenzachse in beiden Darstellungen logarithmisch skaliert ist. Die Normierung auf die Grenzfrequenz bietet sich an, um die Funktionswese des Frequenzganges unabhängig von spezifischen Bauteilwerten darzustellen.
Abbildung 5 zeigt den dazugehörigen Phasengang als Bode-Diagramm ebenfalls mit Normierung der Frequenz auf die Grenzfrequenz. Die Kurvenform des Phasenganges ähnelt der Kurvenform eines Arkustangens in linearer Darstellung bei entsprechender Verschiebung und Stauchung.
Der Wertebereich des Phasenganges wird durch die beiden horizontalen Asymptoten \(\varphi (\omega ) = 0\ ^\circ \) für \(\omega \rightarrow 0\) und \(\varphi (\omega ) = -90\ ^\circ \) für \(\omega \rightarrow \infty \) begrenzt. Der Phasengang besitzt in dieser Darstellungsform eine Punktsymmetrie zum Wendepunkt in \(\varphi (\omega _g) = -45\ ^\circ \) und keine Extrema.
Sei \(\omega _n\) die normierte Frequenz \(\omega /\omega _g\). So lässt sich der Phasengang abschnittsweise durch folgende drei Geradenabschitte approximieren: \begin {equation} \varphi (\omega ) \approx \begin {cases}\begin {aligned}0\ &^\circ &&\text {für}& &\omega _n < 10^{-1} &&\text {Durchlassbereich (ohne Grenzbereich)}\\ -45\ &^\circ + \frac {-45\ ^\circ }{\mathrm {Dek}}\omega _n &&\text {für}& 10^{-1} \leq \ &\omega _n \leq 10 &&\text {Grenzbereich}\\ -90\ &^\circ &&\text {für}& 10 <\ &\omega _n &&\text {Sperrbereich (ohne Grenzbereich)} \end {aligned} \end {cases} \end {equation}
Die maximale Abweichung der Approximation beträgt \(\pm \ 5.71^\circ \) an den Knickstellen bei \(\omega _g\pm 1\ \mathrm {Dek}\).
Zum Vergleich sind in Abbildung 6 der Amplituden- und Phasengang eines Tiefpass 1. Ordnung in linearer und logarithmischer Darstellung (Bode-Diagramm) dargestellt.

Anders als bei linearer Darstellung entspricht bei logarithmischer Darstellung die Ableitung einer Funktionen nicht der ablesbaren Steigung im Kurvenverlauf. In Abbildung 6 ist dies gut erkennbar. Die Steigung von \(A(\omega )\) in linearer Darstellung geht sowohl für \(\omega \to 0\) als auch für \(\omega \to \infty \) zu gegen \(0\). [Vgl. Kapitel ??] Im Bodediagramm ist die Steigung für \(\omega \to 0\) ebenfalls null, nähert sich für \(\omega \to \infty \) jedoch einer minimalen Steigung von \(-20\,\mathrm {dB}/\mathrm {Dek}\) an. Beim Phasengang ist in linearer Darstellung die Steigung (Ableitung) für \(\omega \to 0\) minimal und negativ. In logarithmischer Darstellung scheint \(\varphi (\omega )\) für \(\omega \to 0\) jedoch am flachesten (Steigung gegen \(0\)).
Abbildung 7 zeigt die Frequenzgänge eines Tiefpass und eines Hochpass 1. Ordnung im Bode-Diagramm zum Vergleich. Der Frequenzbereich (x-Achse) ist in beiden Fällen auf die jeweilige Grenzfrequenz normiert.
Bandpass-Filter und Bandsperre-Filter sind Filtertypen zur Filterung von Frequenzbändern.
Ähnlich wie Tief- und Hochpass finden beide eine breite Anwendung in der Signalverarbeitung zum Beispiel im Bereich der Audio-, Nachrichten-, Mess- und Regelungstechnik. Weitere Anwendungen finden sich beispielsweise in der Energietechnik bei der Einspeisung von Energie ins elektrische Versorgungsnetz, um eine stabile Netzfrequenz zu gewährleisten.
Bandpässe filtern Signale außerhalb eines bestimmten Frequenzbandes heraus, während Bandsperren Signale innerhalb eines bestimmten Frequenzbandes herausfiltern. Die Frequenzbänder werden durch eine obere und untere Grenzfrequenz \(f_{\mathrm {go}}\) und \(f_{\mathrm {gu}}\) definiert.
\begin {equation} \left .\frac {\mathrm {U}_2}{\mathrm {U}_1}\right \rvert _{f=f_{\mathrm {go}}} = \frac {1}{\sqrt {2}} \text {und} \left .\frac {\mathrm {U}_2}{\mathrm {U}_1}\right \rvert _{f=f_{\mathrm {gu}}} = \frac {1}{\sqrt {2}} \end {equation}
Daraus abgeleitete Größen sind die Bandbreite \(B\) und die Mittenfrequenz \(f_{\mathrm {M}}\). Die Bandbreite ist definiert als Differenz von oberer und unterer Grenzfrequenz:
\begin {equation} \label {eq:def:b} B = \Delta f = f_{\mathrm {go}} - f_{\mathrm {gu}} \end {equation}
Die Mittenfrequenz \(f_{\mathrm {M}}\) ist definiert als das geometrische Mittel beider Grenzfrequenzen:
\begin {equation} \label {eq:def:fm} f_{\mathrm {M}} = \sqrt {f_{\mathrm {go}} \cdot f_{\mathrm {gu}}} \end {equation}
In logarithmischer Darstellung liegt \(f_{\mathrm {M}}\) qua Definition exakt in der Mitte zwischen beiden Grenzfrequenzen. Dadurch lassen sich mit \(B\) und \(f_{\mathrm {M}}\) Größe und Lage des Frequenzbandes im Frequenzspektrum beschreiben.
Eine mögliche Realisierung von Bandpass- und Bandsperre-Filtern ist durch Kombination eines Tief- und Hochpass-Filters. Auf diese Weise lässt sich anschaulich das Verhalten kombinierter Filterschaltungen erläutern.
Durch die Serienschaltung eines Tief- und Hochpass entsteht ein Bandpass, vorrausgesetzt die Grenzfrequenzen sind passend gewählt. Für ein Bandpassverhalten muss die obere Grenzfrequenz durch den Tiefpass und die untere Grenzfrequenz durch den Hochpass realisiert werden. Mathematisch beschreiben lässt sich der resultierende Frequenzgang als Produkt der Einzelfrequenzgänge mit \(\underline {F}_{\mathrm {BP}} = \underline {F}_{\mathrm {TP}} \cdot \underline {F}_{\mathrm {HP}}\). Vorraussetzung für die Multiplikation der Einzelfrequenzgänge zum Gesamtfrequenzgang ist die Rückwirkungsfreiheit des nachgeschalteten Vierpols auf das Ausgangssignal des vorgeschalteten Vierpols.
Abbildung 8 zeigt exemplarisch das Schaltbild eines solchen Bandpasses zweiter Ordnung als Serienschaltung eines RC-Tiefpasses und eines RC-Hochpasses, beide erster Ordnung. Der symbolische Verstärkerblock zwischen beiden Filter verhindert eine Rückwirkung des Hochpass auf die Ausgangsspannung des Tiefpasses. Nur unter der Annahme einer Rückwirkungsfreiheit lassen sich die Frequenzgänge von Tiefpass und Hochpass durch in Reihe Schalten multiplizieren.
Eine Bandsperre lässt sich realisieren indem die Eingänge von Tief- und Hochpass parallel und deren Ausgänge in Serie geschalten werden. Dadurch erhalten beide Einzelfilter die gleiche Eingangsspannung und die Ausgangsspannungen werden addiert. Der resultierende Frequenzgang ist die Summe der Einzelfrequenzgänge mit \(\underline {F}_{\mathrm {BS}} = \underline {F}_{\mathrm {TP}} + \underline {F}_{\mathrm {HP}}\). In diesem Fall muss die obere Grenzfrequenz durch den Hochpass und die untere Grenzfrequenz durch den Tiefpass realisiert werden.
In Abbildung 9 ist das Bode-Diagramm des Bandpasses aus Abb. 8 dargestellt. Amplitudengang und Phasengang übereinander teilen sich eine gemeinsame X-Achse, zum besseren Vergleich der beiden Graphen. Der Verstärkungsfaktor beträgt \(1\) (passiv) und die Grenzkreisfrequenzen liegen bei \(10^2\,\mathrm {s}^{-1}\) und \(10^4\,\mathrm {s}^{-1}\).
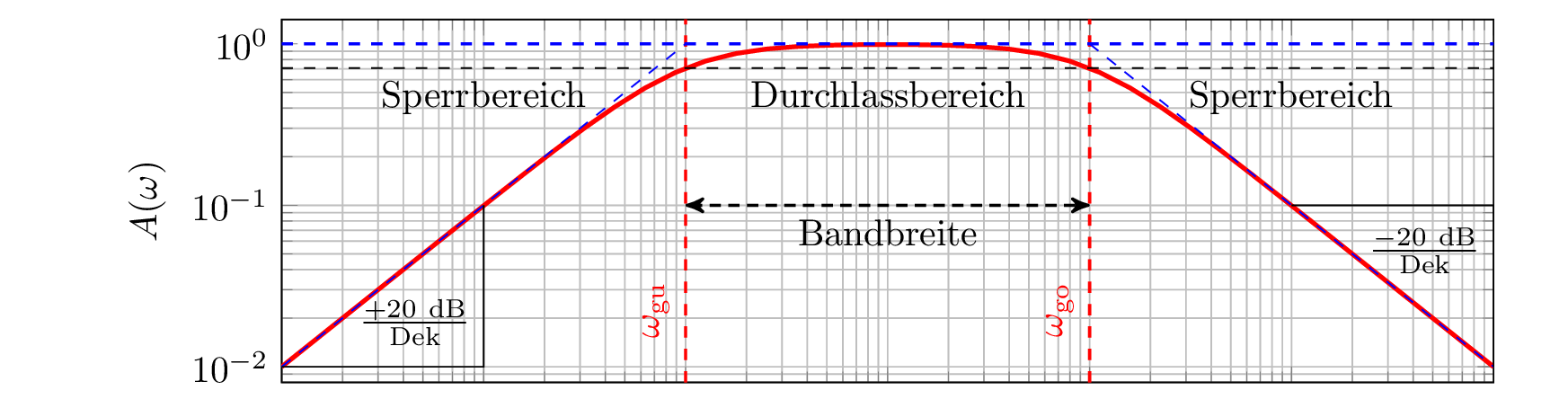
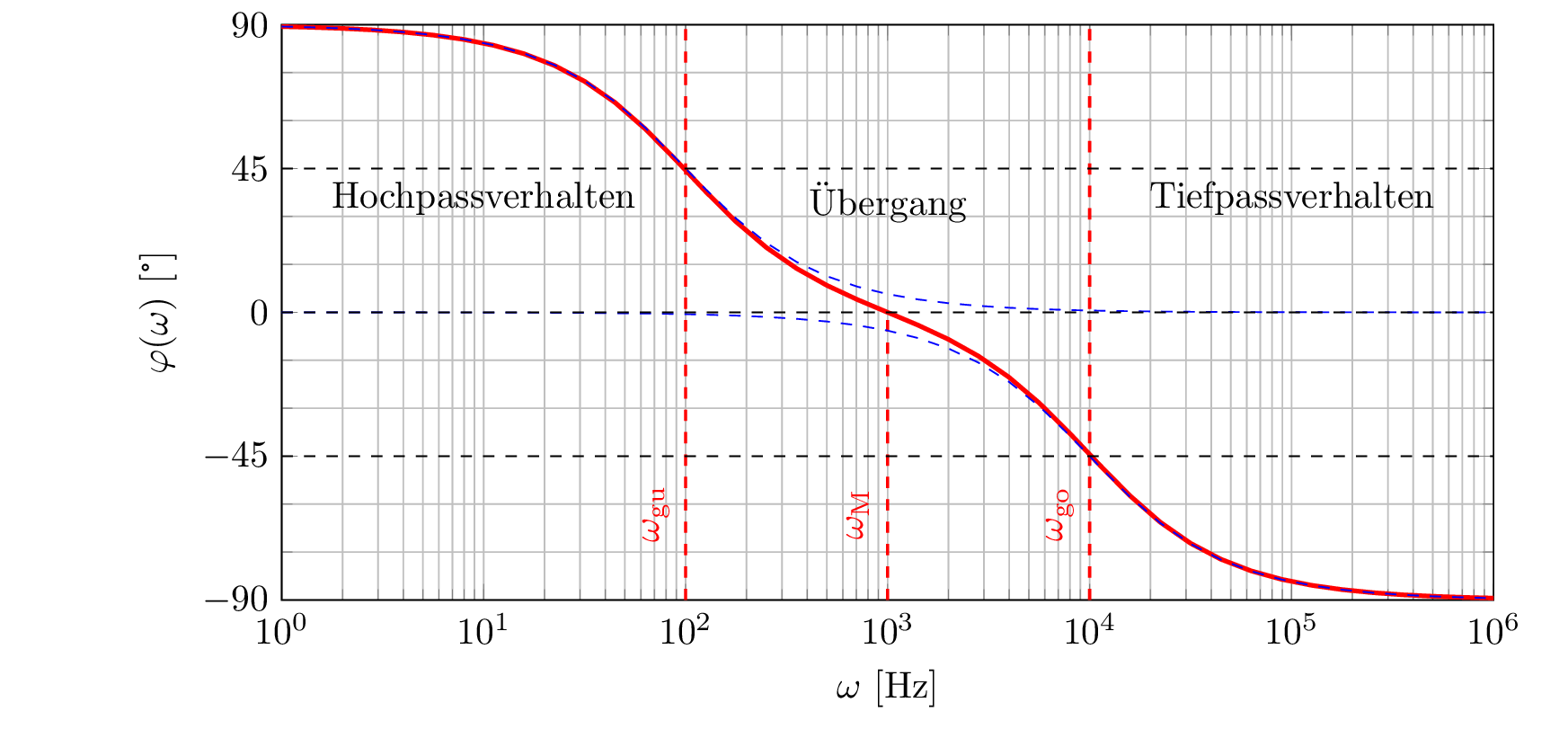
Die obere und untere Grenzkreisfrequenz \(\omega _{\mathrm {go}}\) und \(\omega _{\mathrm {gu}}\) sind in beiden Darstellungen gekennzeichnet (rot gestrichelte, vertikal), ebenso wie die \(-3\,\mathrm {dB}\) Grenze (schwarz gestrichelt, horizontal) deren Schnitt mit \(A(\omega )\) die Grenzfrequenzen definiert.
Die Bandbreite ist im Amplitudengang angedeutet als Doppelfeil zwischen beiden Grenzfrequenzen. Aufgrund der logarithmischen Skalierung entspricht die Bandbreite nicht dem angezeigten geometrischen Abstand im Diagramm.
Im Schaubild abzulesen sind: \begin {align} \omega _{\mathrm {gu}} &= 10^2\,\mathrm {s}^{-1} \qquad \text {und} \qquad \omega _{\mathrm {go}} = 10^4\,\mathrm {s}^{-1}\vphantom {\bigg |}\\ B &\overset {\tiny \ref {eq:def:b}}{=} \Delta f = \frac {\omega _{\mathrm {go}} - \omega _{\mathrm {gu}}}{2\pi } = \frac {9900}{2\pi }\mathrm {Hz}\vphantom {\bigg |}\\ f_{\mathrm {m}} &\overset {\tiny \ref {eq:def:fm}}{=} \frac {\omega _{\mathrm {m}}}{2\pi } = \frac {\sqrt {\omega _{\mathrm {go}} \cdot \omega _{\mathrm {gu}}}}{2\pi } = \frac {10^3}{2\pi }\mathrm {Hz}\vphantom {\bigg |} \end {align}
Die Mittenkreisfrequenz \(\omega _{\mathrm {m}}\) ist im Phasengang gekennzeichnet. Die Phasenverschiebung beträgt dort \(0^\circ \), da sich die Phasenverschiebung des Tief- und Hochpasses (blau gestrichelt, dünn) in dem Punkt gegenseitig aufheben.
Gut zu erkennen ist das Hochpassverhalten im unteren Sperrbereich (mit \(+20\mathrm {dB}/\mathrm {Dek}\) und \(\varphi (\omega ) > 0^\circ \)) und das Tiefpassverhalten im oberen Sperrbereich (mit \(-20\mathrm {dB}/\mathrm {Dek}\) und \(\varphi (\omega ) > 0^\circ \)).
Abbildung 10 zeigt exemplarisch die Amplitudengänge verschiedener Filter höherer Ordnung im Vergleich. Zu erkennen sind ein Butterworth-, ein Tschebycheff-, ein Cauer-Filter im Vergleich mit einem idealen Tiefpass.
Ordnung anhand der summierten Steilheit der Flanken erklären.
Filter 2. Ordnung durch: RLC oder Kombination zweier Filtern 1. Ordnung: 2x (RC) bzw. 2x (RL) (1. Ordnung)
Filter höherer Ordnung als 2 durch Kaskadierung von Filtern niedrigerer Ordnung möglich.
Vgl: Mexle Wiki
Merke:
\(n \cdot 20\ \mathrm {dB}/\mathrm {Dek}\) Steilheit bei Filter \(n\)-ter Ordnung für alle Flanken summiert.
Höhere Ordnung durch Kaskadierung von Filtern niedrigerer Ordnung möglich.
...