Ortskurven

Die Darstellung von Ortskurven ist ein Mittel zur Visualisierung der parameterabhängigen Veränderung von komplexen Größen. Zur Analyse des frequenzvariablen Verhaltens von Eintoren bieten sich Impedanz- und Admittanzortskurven an. In diesen kann die Veränderung der Impedanz respektive der Admittanz in Abhängigkeit der (Kreis-)Frequenz dargestellt werden.

Lernziele: Ortskurven

Studierende lernen:

  • Ortskurven kennen und mögliche Anwendungsbereiche kennen.
  • Ortskurven prinzipiell zu konstruieren und zu interpretieren.
  • Impedanz- und Admittanzortskurven von Grundschaltungen kennen.

1 Definition Ortskurve

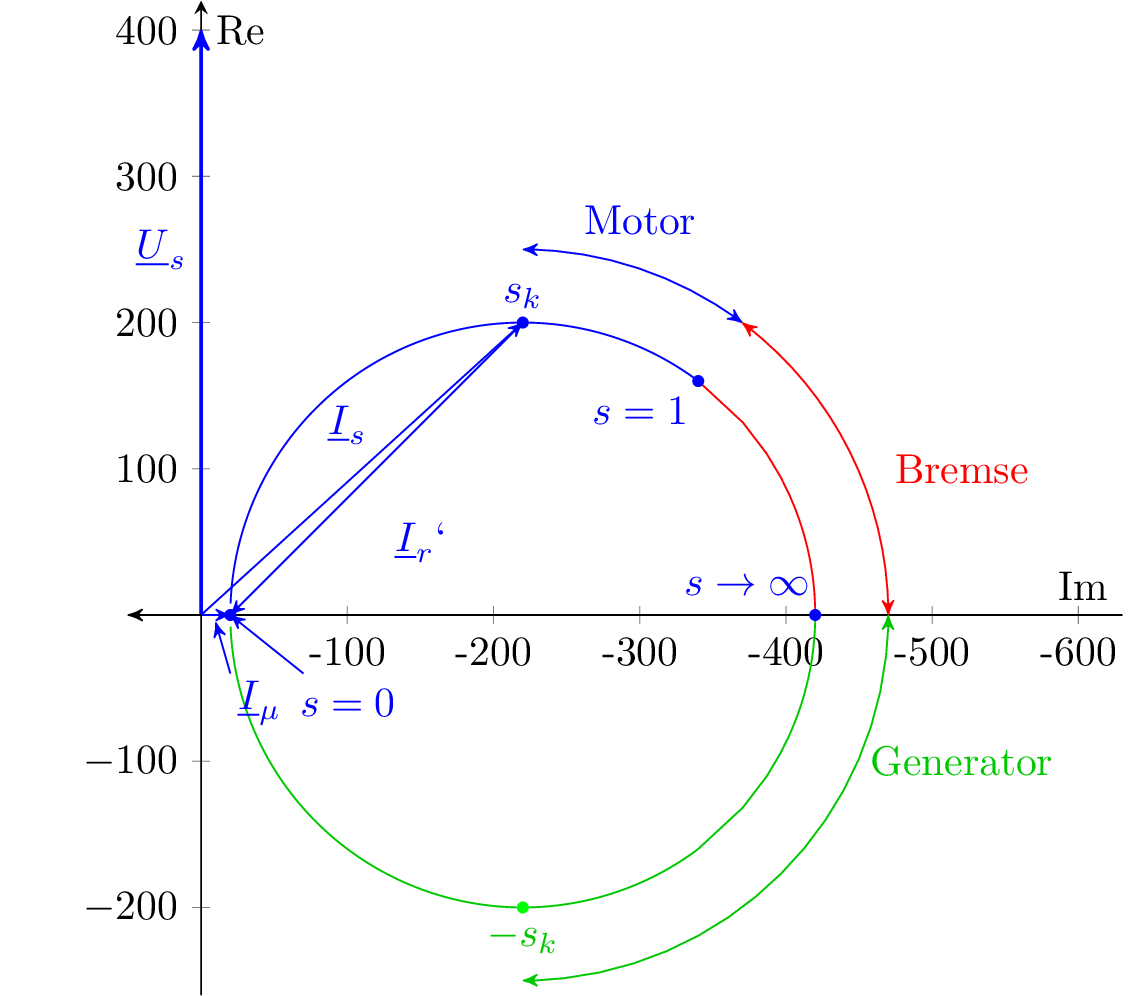
Eine Ortskurve ist die graphische Darstellungen einer komplexen Größe \(\underline {z}\) in Abhängigkeit eines reellen Parameters \(p\) in der komplexen Ebene[?, Vgl. ]: \begin {equation} \begin {aligned} \label {eq:def:ortskurve} \underline {z}(p) &= \Re \{\underline {z}(p)\} + \mathrm {j}\Im \{\underline {z}(p)\} &&\text {mit }\underline {z}\in \mathbb {C};\ p\in \mathbb {R} \end {aligned} \end {equation}Ortskurven werden in vielen verschiedenen Bereichen angewandt, um mögliche Zustände eines Systems zu visualisieren. Abbildung 1 zeigt exemplarisch die Stromortskurve einer Asynchronmaschine in der komplexen Ebene, auch Heylandkreis oder Ossannakreis genannt. [QUELLE:XYZ] Zu Erkennen ist der komplexe Statorstrom \(\underline {I}_s\) in Abhängigkeit des Schlupfes \(s\). Die Darstellungsform eignet sich beispielsweise zur Visualisierung verschiedener Betriebszustände, im Fall der Asynchronmaschine sind das der Motor-, Brems- und Generatorbetrieb.

PIC

Abbildung 1: Beispiel Stromortskurve einer Asynchrommaschine mit Betriebszuständen

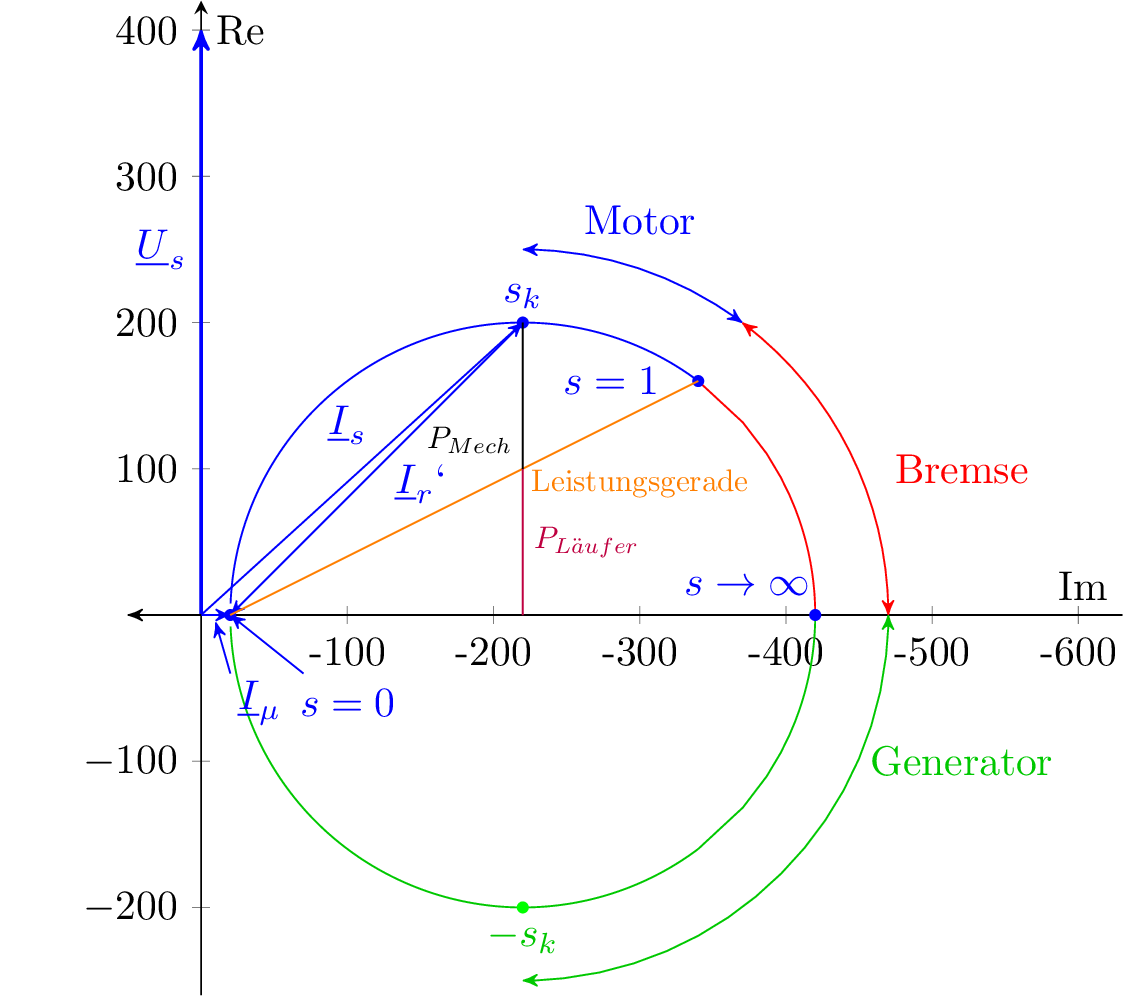
Im Beispiel der Stromortskurve einer Asynchronmaschine lassen sich zudem verschiedene Leistungswerte graphisch ermitteln wie in Abbildung 2 exemplarisch dargestellt ist. Die Beispiele dienen der Veranschaulichung der Definition und möglicher Anwendungsbereiche von Ortskurven, weshalb von einer Herleitung beider Beispiele abgesehen wird.

PIC

Abbildung 2: Beispiel Stromortskurve einer Asynchrommaschine mit Leistungsgrößen

Ortskurven eignen sich gut zur Visualisierung von Systemzuständen, -größen und deren Einfluss aufeinander.

2 Zusammenhang Zeigerdiagramm und Ortskurve

Ein Zeiger im Zeigerdiagramm stellt eine komplexe Größe stationär in der komplexen Ebene dar. Die Darstellungsform dient der Visualisierung von Phasenverschiebungen und Betragsverhältnissen. Typische Größen für Wechselstromkreise sind unter anderem Spannung, Strom, Leistung und Impedanz.

Ortskurven beschreiben die Bahn, die ein Zeiger bei Variation eines Parameters durchläuft. Die Ortskurve kann so als Verallgemeinerung eines Zeigers im Zeigerdiagramm verstanden werden. [?, Vgl.]Übliche Parameter sind Frequenz und Bauteilgrößen.

Die Hervorhebung einzelner Zeiger mit Angabe des variierenden Parameters kann den Verlauf der Ortskurve verdeutlichen und die Interpretation erleichtern. Positionsänderungsrate und -richtung geben Aufschluss über die Dynamik des Systems.

Merke: Ortskurve

Zeigt Größe in komplexer Ebene parameterabhängig als Kurve (Punkteschar).

3 Impedanzortskurve

In Impedanzortskurven wird die Impedanz eines Systems in Abhängigkeit eines Parameters dargestellt.

Beispiel ?? zeigt eine Impedanzortskurve für eine variable Bauteilgröße.

Beispiel ?? zeigt eine Impedanzortskurve für variable Frequenz.

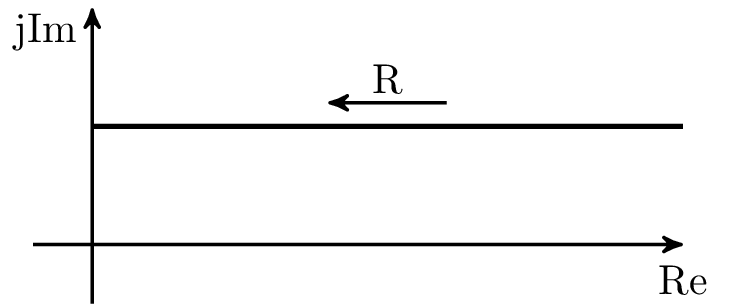
Beispiel 1:  Impedanzortskurve RL-Glied, Widerstand variabel

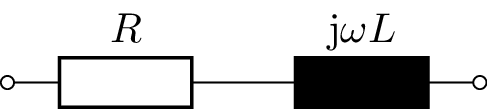
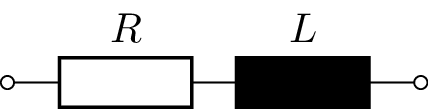
Konstruktion der Impedanzortskurve einer RL-Serienschaltung für variablen Widerstand \(R\). Die Schaltung ist in Abbildung 3 abgebildet.

PIC

Abbildung 3: RL-Glied (Serienschaltung)

Die Impedanz des RL-Gliedes ist gegeben durch:

\begin {equation*} \underline {Z} = R + \mathrm {j}\omega L \end {equation*}

Sei \(R\) variabel und beschrieben als (\(p\)-fache) Vielfache eines Referenzwiderstandes \(R_0\) mit \(p\) im geschlossenen Intervall \([0,3]\), so gilt:

\begin {equation*} R(p) = p \cdot R_0 \quad \text {mit } p \in [0,3] \end {equation*}

Seien \(\omega \) und \(L\) konstant, sowie die Reaktanz \(\omega L\) gleich einer Referenzreaktanz \(X_0\):

\begin {equation*} \omega L = X_0 \quad \text {mit } \omega ,\ L = konst. \end {equation*}

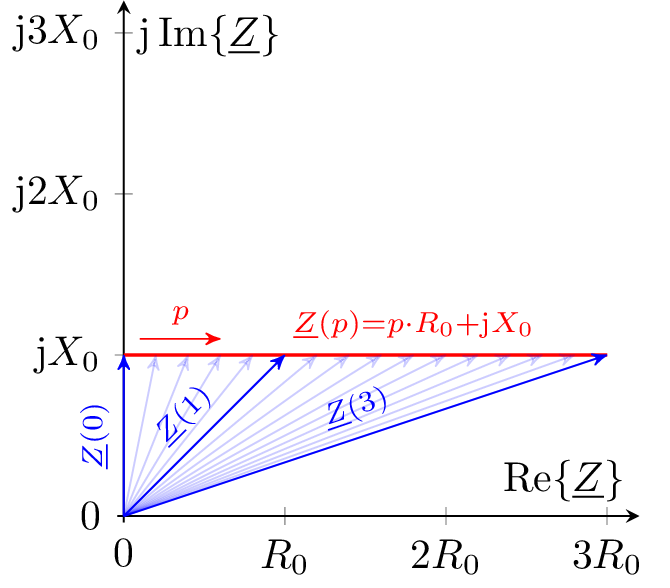
Impedanz \(\underline {Z}\) in Abhängigkeit von \(p\):

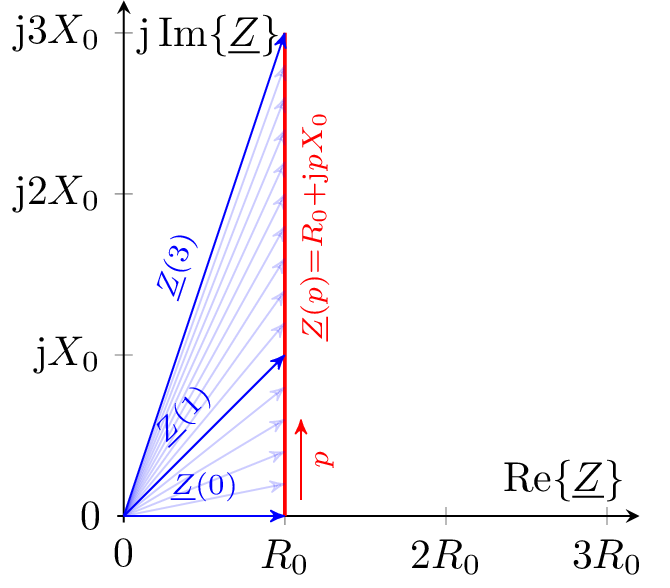
\begin {equation*} \underline {Z}(p) = p \cdot R_0 + \mathrm {j}X_0 \end {equation*}

PIC

Abbildung 4: Impedanzortskurve RL-Glied (Serie)

Beispiel 2: Impedanzortskurve RL-Glied, Frequenz variabel

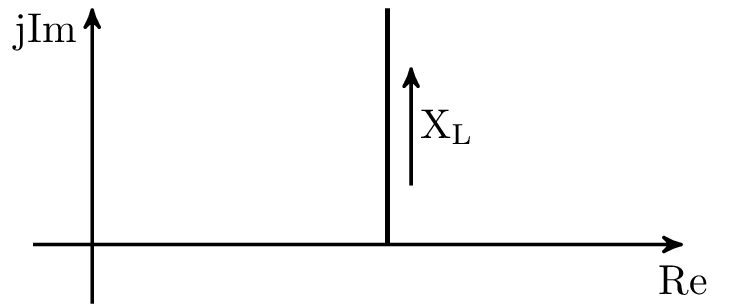
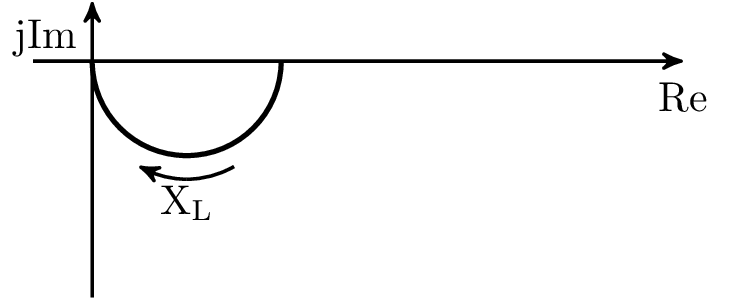
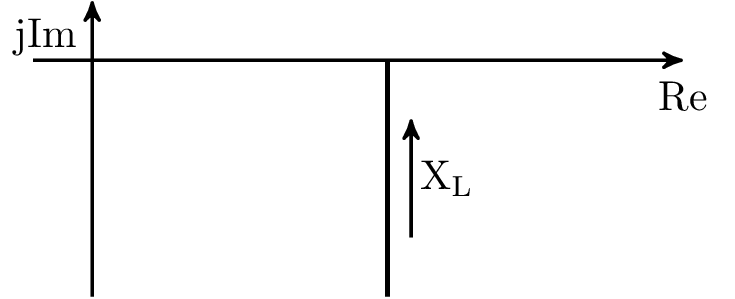
Konstruktion der Impedanzortskurve der RL-Serienschaltung in Abbildung 5 für variable Frequenz \(f\) und oder variable Induktivität \(L\). Aufbau wie in Beispiel ??, jedoch mit variabler Frequenz \(\omega \).

PIC

Abbildung 5: RL-Glied (Serienschaltung)

Gesamtimpedanz allgemein: \begin {align*} \underline {Z} &= R + \mathrm {j}\omega L \\ &= R + \mathrm {j}X \end {align*}

Die Gesamt-Reaktanz \(X\) des RL-Gliedes ist proportional zu \(\omega \) und proportional zu \(L\). Das heißt eine Veränderung von \(\omega \) hat den selben Einfluss wie eine Veränderung von \(L\) auf die Impedanz des RL-Gliedes.

Mit \(X\) als Vielfache \(p\) einer Referenz-Reaktanz \(X_0\) und \(R=R_0\) gilt:

\begin {equation*} \underline {Z} = R_0 + p \cdot \mathrm {j}X_0 \end {equation*}

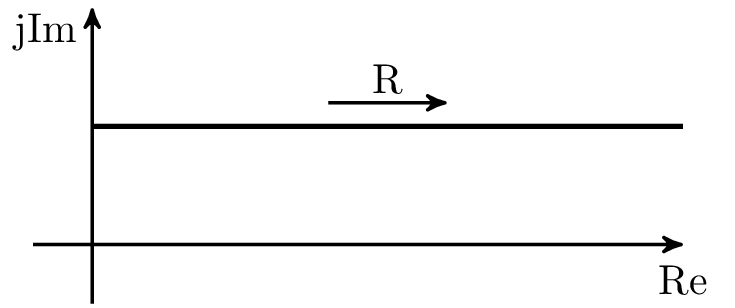
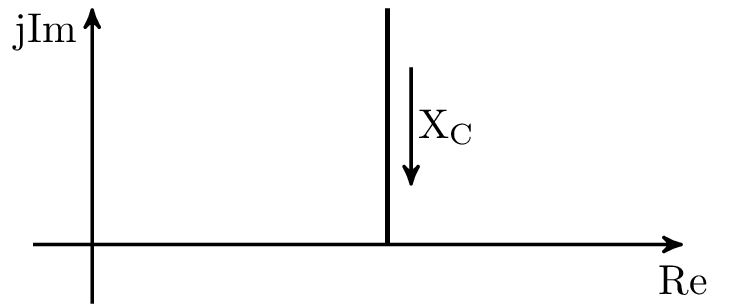
In der komplexen Ebene dargestellt:

PIC

Abbildung 6: RL-Glied (Serienschaltung)

4 Admittanzortskurve - Inversion von Ortskurven

Analog zur Impedanzkurve bezeichnet eine Admittanzkurve die Ortskurve einer Admittanz. Die Admittanz \(\underline {Y}\) entspricht algebraisch dem Kehrwert der Impedanz \(\underline {Z}\) und vice versa:

\begin {equation} \underline {Y} = \frac {1}{\underline {Z}} \quad \leftrightarrow \quad \underline {Z} = \frac {1}{\underline {Y}} \end {equation}

Die Umformung von Impedanz zu Admittanz und umgekehrt ist jeweils ein Spezialfall der Möbius-Transformation.

Für die Beziehung zwischen Admittanz- und Impedanzortskurven gelten daher folgende allgemeinen Eigenschaften von Möbius-Transformation: [?, Vgl. ]

  • Winkeltreue: \(\angle (\underline {Z_1},\underline {Z_2}) = \angle (\underline {Y_1},\underline {Y_2}) \qquad \text {mit } \underline {Y}_i = \underline {Z}_i^{-1},\ i \in [1,2]\)
  • Kreisverwandschaft: Kreise und Geraden werden auf Kreise und Geraden abgebildet

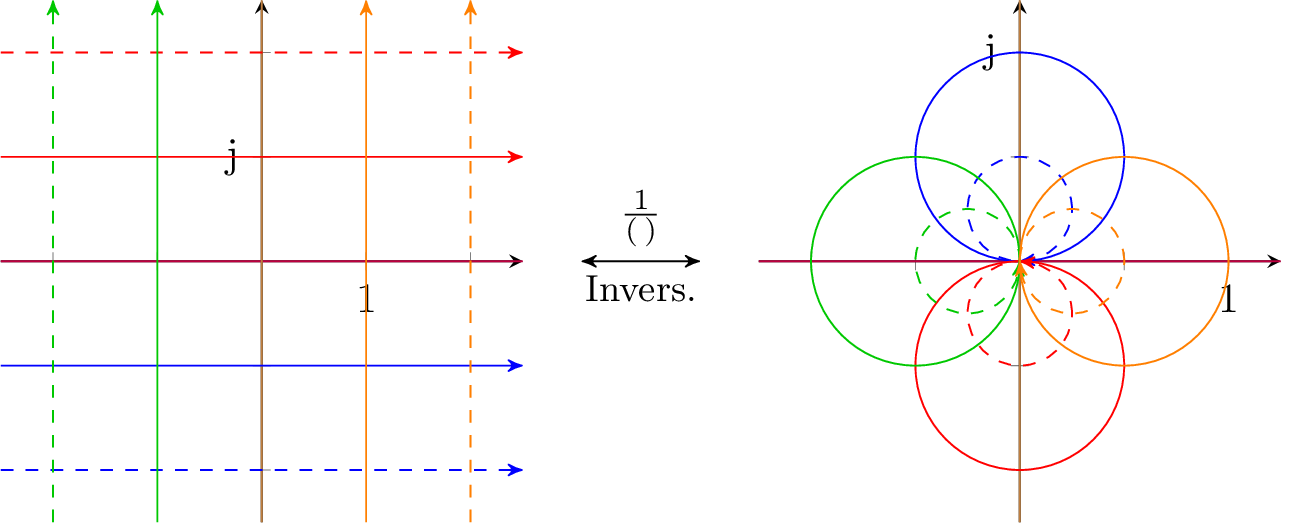
Die Kehrwertbildung entspricht im speziellen der Inversion, einem Elementartyp der Möbius-Transformation. Eine Inversion von Ortskurven führt zu den in Tabelle 1 aufgelisteten geometrischen Umformungen von Kreisen und Geraden. Abbildung 7 zeigt exemplarisch die Inversion eines Gitters durch den Ursprung.

Tabelle 1: Typische Formen bei Inversion von Ortskurven
ursprüngliche Ortskurve invertierte Ortskurve
Gerade durch den Ursprung Gerade durch den Ursprung
Gerade nicht durch den Ursprung Kreis durch den Ursprung
Kreis durch den Ursprung Gerade nicht durch den Ursprung
Kreis nicht durch den Ursprung Kreis nicht durch den Ursprung

PIC

Abbildung 7: Beispiel Möbius-Transformation, Inversion von Gitter1

5 Ortskurven von Grundschaltungen

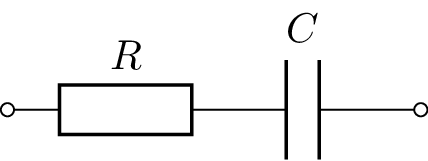
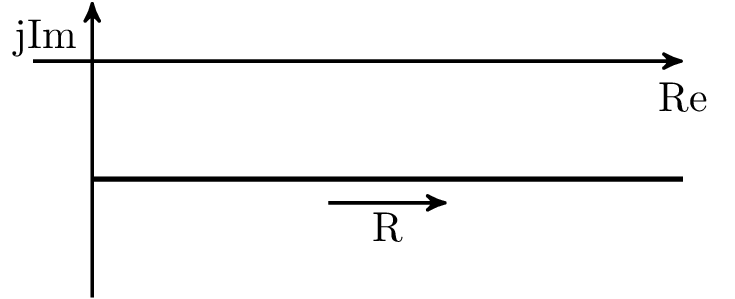
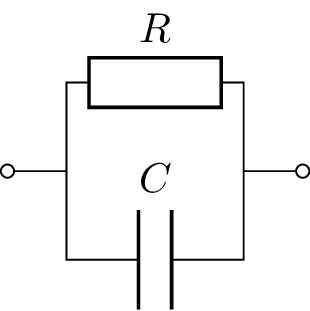
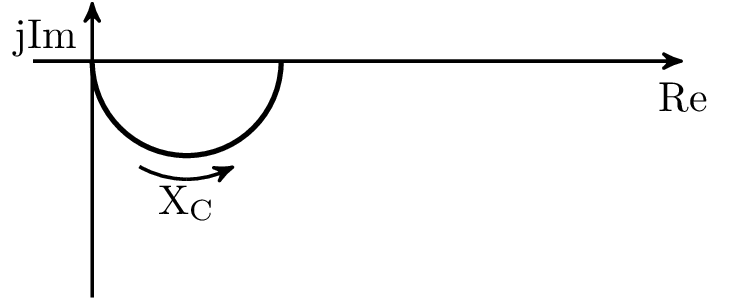
Tabelle 2 zeigt eine Übersicht der Impedanz- und Admittanzortskurven für die vier Grundschaltungen RL- und RC-Glied jeweils in Serien- und Parallelschaltung.

Ortskurven schwingungsfähiger LC- und RLC-Glieder unterscheiden sich von den hier dargestellen Ortskurven dadurch, dass der Blindanteil der Impedanz bzw. Admittanz je nach Frequenzbereich sowohl induktiv als auch kapazitiv sein kann, je nachdem welcher Anteil überwiegt.

Tabelle 2: Ortskurven der Grundschaltungen RL- und RC-Glied
\(\vphantom {\bigg |}\)Grundschaltung \(\mathbf {\underline {Z}}\)-Ortskurve \(\mathbf {\underline {Y}}\)-Ortskurve
PIC PIC
PIC 		PIC
PIC
PIC PIC
PIC 		PIC
PIC
PIC PIC
PIC 		PIC
PIC
PIC PIC
PIC 		PIC
PIC

1Angelehnt an MoebiusInversion.svg von Chrislb, CC-BY-SA-2.0-DE, 2005, https://commons.wikimedia.org/wiki/File:MoebiusInversion.svg

Expand
×

...